Colab Notebook

Introduction

  • This tutorial offers an overview of the preliminary setup, training process, loss functions and optimizers in PyTorch.
  • We cover a practical demonstration of PyTorch with an example from Vision and another from NLP.

Getting started

Creating a virtual environment

  • To accommodate the fact that different projects you’ll be working on utilize different versions of Python modules, it is a good practice to have multiple virtual environments to work on different projects.
  • Python Setup: Remote vs. Local offers an in-depth coverage of the various remote and local options available.

Using a GPU?

  • Note that your GPU needs to be set up first (drivers, CUDA and CuDNN).
  • For PyTorch, code changes are needed to support a GPU (unlike TensorFlow which can transparently handle GPU-usage) – follow the instructions here.
  • We recommend the following code hierarchy to organize your data, model code, experiments, results and logs:
data/
    train/
    dev/
    test/
experiments/
model/
    *.py
build_dataset.py
train.py
search_hyperparams.py
synthesize_results.py
evaluate.py
  • Purpose each file or directory serves:
    • data/: will contain all the data of the project (generally not stored on GitHub), with an explicit train/dev/test split.
    • experiments: contains the different experiments (will be explained in the following section).
    • model/: module defining the model and functions used in train or eval. Different for our PyTorch and TensorFlow examples.
    • build_dataset.py: creates or transforms the dataset, build the split into train/dev/test.
    • train.py: train the model on the input data, and evaluate each epoch on the dev set.
    • search_hyperparams.py: run train.py multiple times with different hyperparameters.
    • synthesize_results.py: explore different experiments in a directory and display a nice table of the results.
    • evaluate.py: evaluate the model on the test set (should be run once at the end of your project).

Running experiments

  • To train a model on the data, the recommended user-interface for train.py should be:
python train.py --model_dir experiments/base_model
  • We need to pass the model directory in argument, where the hyperparameters are stored in a JSON file named params.json. Different experiments will be stored in different directories, each with their own params.json file. Here is an example:

experiments/base_model/params.json:

{
"learning_rate": 1e-3,
"batch_size": 32,
"num_epochs": 20
}

The structure of experiments after running a few different models might look like this (try to give meaningful names to the directories depending on what experiment you are running):

experiments/
    base_model/
        params.json
        ...
    learning_rate/
        lr_0.1/
            params.json
        lr_0.01/
            params.json
    batch_norm/
        params.json

Each directory after training will contain multiple things:

  • params.json: the list of hyperparameters, in JSON format
  • train.log: the training log (everything we print to the console)
  • train_summaries: train summaries for TensorBoard (TensorFlow only)
  • eval_summaries: eval summaries for TensorBoard (TensorFlow only)
  • last_weights: weights saved from the 5 last epochs
  • best_weights: best weights (based on dev accuracy)

Training and evaluation

  • To train a model with the parameters provided in the configuration file experiments/base_model/params.json, the recommended user-interface is:
python train.py --model_dir experiments/base_model
  • Once training is done, we can evaluate on the test set using:
python evaluate.py --model_dir experiments/base_model
  • We provide an example that will call train.py with different values of learning rate. We first create a directory with a params.json file that contains the other hyperparameters.
experiments/
    learning_rate/
        params.json

  • Next, call python python search_hyperparams.py --parent_dir experiments/learning_rate to train and evaluate a model with different values of learning rate defined in search_hyperparams.py. This will create a new directory for each experiment under experiments/learning_rate/.

  • The output would resemble the hierarchy below:

experiments/
    learning_rate/
        learning_rate_0.001/
            metrics_eval_best_weights.json
        learning_rate_0.01/
            metrics_eval_best_weights.json
        ...

Display the results of multiple experiments

  • If you want to aggregate the metrics computed in each experiment (the metrics_eval_best_weights.json files), the recommended user-interface is:
python synthesize_results.py --parent_dir experiments/learning_rate
  • It will display a table synthesizing the results like this that is compatible with markdown:
  accuracy loss
base_model 0.989 0.0550
learning_rate/learning_rate_0.01 0.939 0.0324
learning_rate/learning_rate_0.001 0.979 0.0623

PyTorch Introduction

Goals of this tutorial

  • Learn more about PyTorch.
  • Learn an example of how to correctly structure a deep learning project in PyTorch.
  • Understand the key aspects of the code well-enough to modify it to suit your needs.

Resources

  • The main PyTorch homepage.
  • The official tutorials cover a wide variety of use cases- attention based sequence to sequence models, Deep Q-Networks, neural transfer and much more!
  • A quick crash course in PyTorch.
  • Justin Johnson’s repository introduces fundamental PyTorch concepts through self-contained examples.
  • Tons of resources in this list.

Code Layout

  • We recommend the following code hierarchy to organize your data, model code, experiments, results and logs:
data/
experiments/
model/
    net.py
    data_loader.py
train.py
evaluate.py
search_hyperparams.py
synthesize_results.py
evaluate.py
utils.py
  • model/net.py: specifies the neural network architecture, the loss function and evaluation metrics
  • model/data_loader.py: specifies how the data should be fed to the network
  • train.py: contains the main training loop
  • evaluate.py: contains the main loop for evaluating the model

  • utils.py: utility functions for handling hyperparams/logging/storing model

  • We recommend reading through train.py to get a high-level overview.

  • Once you get the high-level idea, depending on your task and dataset, you might want to modify:
    • model/net.py to change the model, i.e., how you transform your input into your prediction as well as your loss, etc.
    • model/data_loader.py to change the way you feed data to the model.
    • train.py and evaluate.py to make changes specific to your problem, if required

Tensors and variables

  • Before going further, we strongly suggest going through 60 Minute Blitz with PyTorch to gain an understanding of PyTorch basics. This section offers a sneak peak into the same concepts.

  • PyTorch Tensors are similar in behavior to NumPy’s arrays.

import torch

a = torch.Tensor([[1, 2], [3, 4]])
print(a)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1., 2.],
               #         [3., 4.]])           
print(a.dtype) # Prints torch.float32  

print(a**2)    # Prints a torch.FloatTensor of size 2x2 
               # tensor([[ 1.,  4.],
               #         [ 9., 16.]])
  • Note that torch.tensor() infers the datatype dtype automatically, while torch.Tensor() always returns a torch.FloatTensor.
import torch

# Creating a IntTensor
a = torch.tensor([[1, 2], [3, 4]])
print(a)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1., 2.],
               #         [3., 4.]])
print(a.dtype) # Prints torch.int64

# Creating a FloatTensor
a = torch.tensor([[1., 2.], [3., 4.]])
print(a)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1., 2.],
               #         [3., 4.]])
print(a.dtype) # Prints torch.float32
  • torch.tensor() supports the dtype argument, if you would like to change the type while defining the tensor. Put simply, a tensor of specific data type can be constructed by passing a torch.dtype to the constructor or tensor creation op:
torch.zeros([2, 4], dtype=torch.int32)                # Prints tensor([[ 0,  0,  0,  0],
                                                      #                [ 0,  0,  0,  0]], dtype=torch.int32)
  • Similarly, you can pass in a torch.device argument to the constructor:
cuda0 = torch.device('cuda:0')
torch.ones([2, 4], dtype=torch.float64, device=cuda0) # Prints tensor([[ 1.0000,  1.0000,  1.0000,  1.0000],
                                                      #                [ 1.0000,  1.0000,  1.0000,  1.0000]], dtype=torch.float64, device='cuda:0')

Changing datatypes

  • With PyTorch, the default float datatype is float32 (single precision), while that with NumPy is float64 (double precision). However, the default int datatype for both PyTorch and NumPy is int64. You may also change default floating point dtype to be torch.float64 while defining the tensor:
import torch

torch.set_default_dtype(torch.float64)
a = torch.Tensor([[1, 2], [3, 4]])
print(a)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1., 2.],
               #         [3., 4.]])           
print(a.dtype) # Prints torch.float64

torch.set_default_dtype(torch.float64)
a = torch.tensor([[1., 2.], [3., 4.]])
print(a)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1., 2.],
               #         [3., 4.]])           
print(a.dtype) # Prints torch.float64
  • You may also change the tensor’s datatype after the tensor is defined:
import torch

a = torch.tensor([[1, 2], [3, 4]])
print(a)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1, 2],
               #         [3, 4]])           
print(a.dtype) # Prints torch.float32

b = a.double()
print(b)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1., 2.],
               #         [3., 4.]])           
print(b.dtype) # Prints torch.float64

# Same as "b"
c = a.type('torch.DoubleTensor')
print(c)       # Prints a torch.FloatTensor of size 2x2 
               # tensor([[1., 2.],
               #         [3., 4.]])           
print(c.dtype) # Prints torch.float64

d = c.long()
print(d)       # Prints a torch.LongTensor of size 2x2 
               # tensor([[1, 2],
               #         [3, 4]])           
print(d.dtype) # Prints torch.int64

# Same as "d"
e = c.type('torch.LongTensor')
print(e)       # Prints a torch.LongTensor of size 2x2 
               # tensor([[1, 2],
               #         [3, 4]])          
print(e.dtype) # Prints torch.int64

Automatic differentiation

  • PyTorch Variables allow you to wrap a Tensor and record operations performed on it. This allows you to perform automatic differentiation.
import torch
from torch.autograd import Variable

a = Variable(torch.Tensor([[1, 2], [3, 4]]), requires_grad=True)
print(a)            # Prints a torch.FloatTensor of size 2x2 
                    # tensor([[1., 2.],
                    #         [3., 4.]], requires_grad=True)

b = torch.sum(a**2) # 1 + 4 + 9 + 16
print(b)            # Prints a torch.FloatTensor of size 1
                    # tensor(30., grad_fn=<SumBackward0>)


b.backward()        # compute gradients of b wrt a
print(a.grad)       # print db/da_ij = 2*a_ij for a_11, a_12, a21, a22
                    # Prints a torch.FloatTensor of size 2x2
                    # tensor([[2., 4.], 
                    #         [6., 8.]])

  • This prelude should give you a sense of the things to come. PyTorch packs elegance and expressiveness in its minimalist and intuitive syntax. Make sure to familiarize yourself with some more examples from the resources section before moving ahead.

  • Thus, if you set requires_grad to True for any tensor, PyTorch will automatically track and calculate gradients for that tensor. Now, why is this needed? Setting requires_grad=Tue tells PyTorch that this parameter should be optimized during the training process using backpropagation, when gradients are used to update weights. This is done with the tensor.backward() method; during this operation tensors with requires_grad=True will be used along with the tensor used to call tensor.backward() to calculate the gradients. As a practical example, using plain torch.Tensors (rather than using torch.autograd.Variable as above):

import torch

a = torch.tensor(1.0, requires_grad=True)
x = a ** 3    # x=a^3
b = torch.tensor(1.0, requires_grad=False)
y = b ** 3    # y=b^3
c = torch.tensor(1.0, requires_grad=False)
z = c ** a    # y=b^3

x.backward()  # Computes the gradient 
y.backward()  # Computes the gradient 
z.backward()  # Computes the gradient 

print(a.grad) # this is dx/da; prints tensor(3.)
print(b.grad) # this is dy/db; prints None
print(c.grad) # this is dz/dc; prints None
  • Note that requires_grad defaults to False, unless wrapped in a nn.Parameter().
  • For more, refer PyTorch: Autograd Mechanics.
  • The following sections talk about disabling automatic differentiation using requires_grad=False to freeze model weights (corresponding to some or all layers or even at the level of the individual weights of layers).

Disabling automatic differentiation

Using requires_grad=False

import torch

a = torch.tensor(1.0, requires_grad=False)
x = a ** 3    # x=a^3

x.backward()  # Computes the gradient 

print(a.grad) # this is dx/da; prints None
  • If you want to freeze part of your model and train the rest, you can set requires_grad of the parameters you want to freeze to False.
  • For example, if you only want to keep the convolutional part of VGG16 fixed:
model = torchvision.models.vgg16(pretrained=True)
for param in model.features.parameters():
    param.requires_grad = False
  • By switching the requires_grad flags to False, no intermediate buffers will be saved, until the computation gets to some point where one of the inputs of the operation requires the gradient.

Using torch.no_grad()

  • Using the context manager torch.no_grad() is a different way to achieve that goal: in the no_grad context, all the results of the computations will have requires_grad=False, even if the inputs have requires_grad=True.

  • Notice that you won’t be able to backpropagate the gradient to layers before the torch.no_grad, which are lin1 and lin1 in the below example.

      x = torch.randn(2, 2)
  x.requires_grad = True

  lin0 = nn.Linear(2, 2)
  lin1 = nn.Linear(2, 2)
  lin2 = nn.Linear(2, 2)
  x1 = lin0(x)
    
  with torch.no_grad():    
      x2 = lin1(x1)
    
  x3 = lin2(x2)
  x3.sum().backward()
    
  print(lin0.weight.grad, lin1.weight.grad, lin2.weight.grad)
    • which outputs:
      (None, None, tensor([[-1.4481, -1.1789],
           [-1.4481, -1.1789]]))
  • Thus, lin1.weight.requires_grad was True in the above example, but the gradient wasn’t computed because the operation was done in the no_grad context.
  • If your goal is not to finetune, but to set your model in inference mode, the most convenient way is to use the torch.no_grad context manager. In this case you also have to set your model to evaluation mode, this is achieved by calling eval() on the nn.Module, for example:
model = torchvision.models.vgg16(pretrained=True)
model.eval()
  • This operation sets the attribute self.training of the layers to False, which changes the behavior of operations like Dropout or BatchNorm that behave differently at training vs. test time.

Parameters

  • A tensor can be wrapped in a nn.Parameter() call to create a parameter for your nn.module. Note that the only difference between a torch.tensor and a nn.Parameter is that an nn.Parameter is tracked as a model parameter (and you may list all such parameters for the particular module using nn.Module.parameters()).

nn.Parameter internals

  • The nn.Parameter class is shown in the below code snippet:

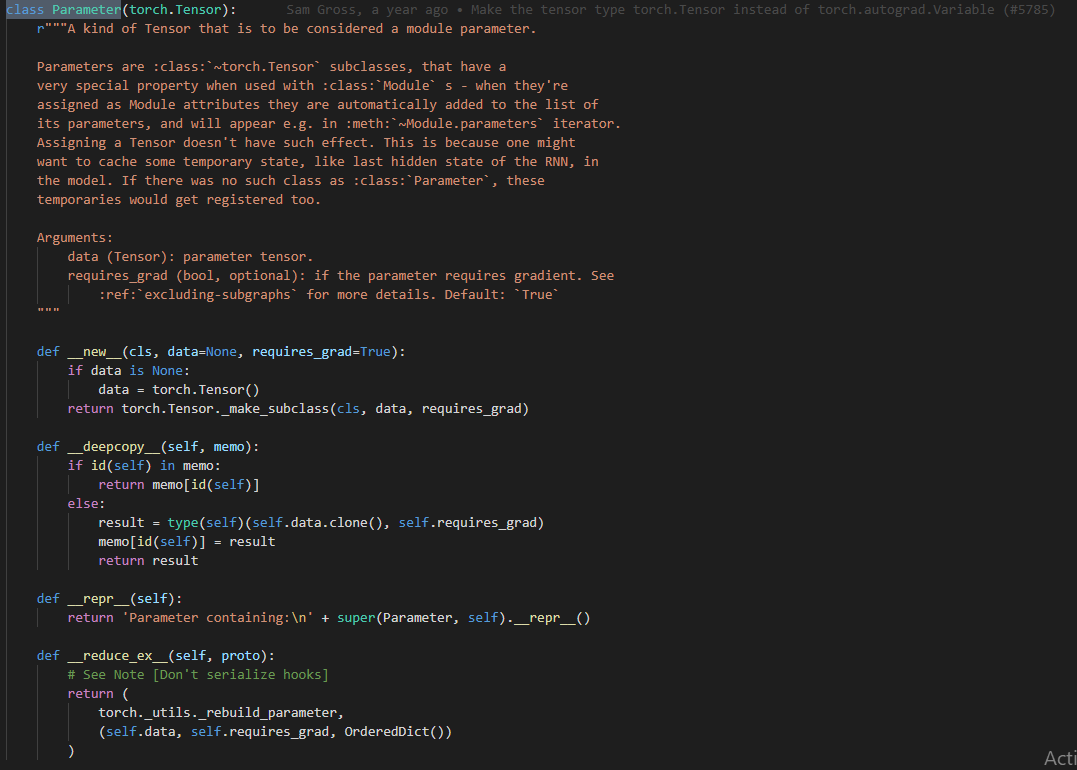
  • Note that since it is sub-classed from Tensor it is effectively a Tensor (with added features).

Difference between Parameter vs. Tensor in PyTorch

  • Parameters that are declared using nn.parameter inside of a module are added to the list of the Module’s parameters. Say, if m is your module, m.parameters() will book-keep your parameters.

  • As an example:

import torch.nn as nn

class M(nn.Module):
    def __init__(self):
        super().__init__()
        self.weights = nn.Parameter(torch.randn(2, 2))
        self.bias = nn.Parameter(torch.zeros(2))

    def forward(self, x):
        return x @ self.weights + self.bias

m = M()
m.parameters()
list(m.parameters())
# Prints
# [Parameter containing:
#  tensor([[ 0.1506,  1.2606],
#          [-1.7916, -0.2112]], requires_grad=True), 
#  Parameter containing:
#  tensor([0., 0.], requires_grad=True)]
  • nn.Module.parameters() returns the parameters that were defined. On the flip side, if we just define a tensor within the class, using say, self.t = torch.tensor(1), it will not show up in the parameters list. That is the only difference between a torch.tensor and a nn.Parameter.

Core training step

  • Let’s begin with a look at what the heart of our training algorithm looks like. The five lines below pass a batch of inputs through the model, calculate the loss, perform backpropagation and update the parameters.
output_batch = model(train_batch)           # compute model output
loss = loss_fn(output_batch, labels_batch)  # calculate loss

optimizer.zero_grad()                       # clear previous gradients (can also be done right after optimizer.step())
loss.backward()                             # compute gradients of loss w.r.t. the inputs and parameters
                        
optimizer.step()                            # perform updates using the calculated gradients

  • Each of the variables train_batch, labels_batch, output_batch and loss is a PyTorch Variable which allows derivatives to be automatically calculated.

  • All the other code that we write is built around this – the exact specification of the model, how to fetch a batch of data and labels, computation of the loss and the details of the optimizer.
  • These steps are visually summarized in the image (credits to Daniel Bourke) below:

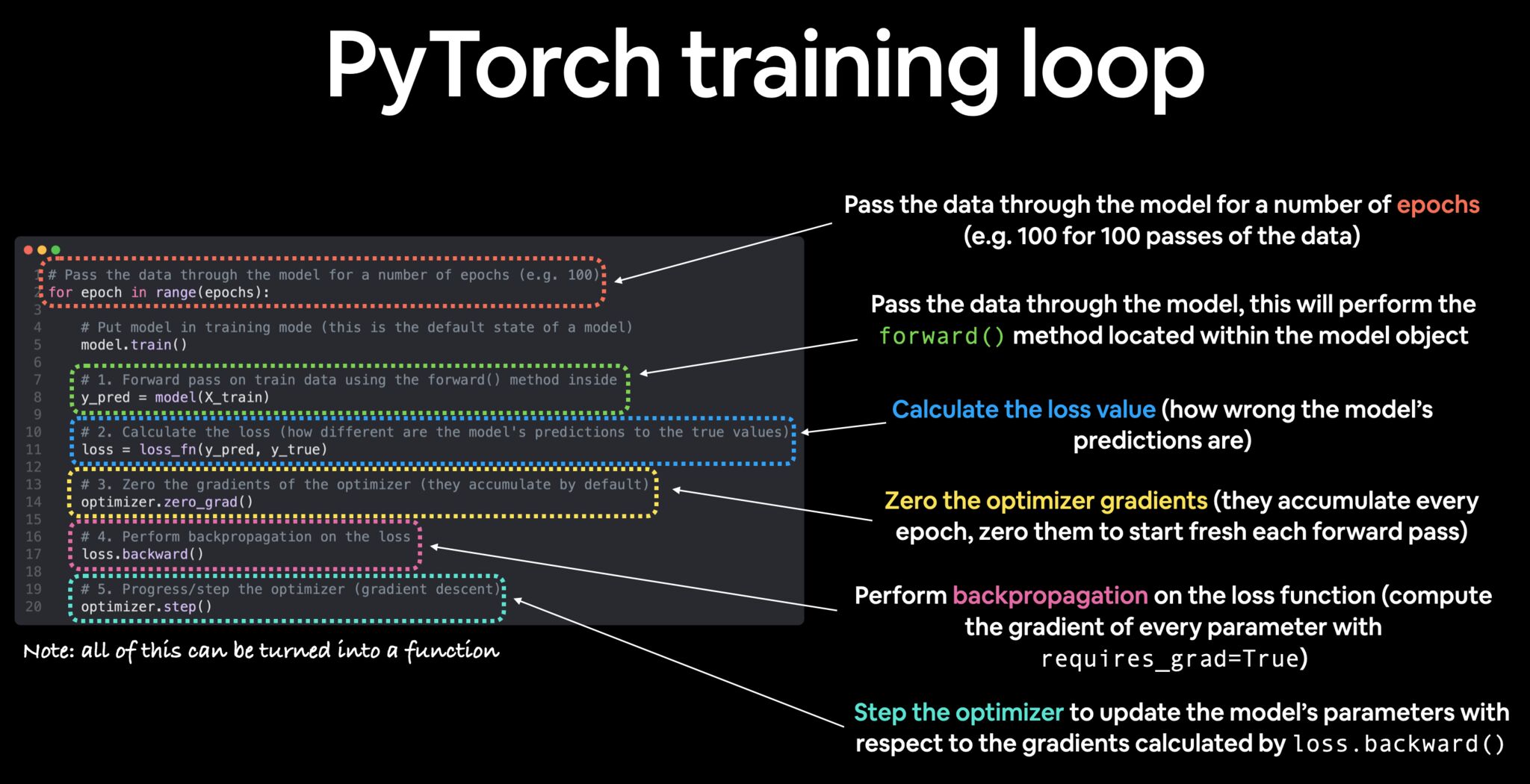
  • The PyTorch training loop is a five step process:
    • Step 1: The Forward pass.
      • Here, the model takes your data, feeds it forward through your network architecture, and comes up with a prediction.
      • First, put the model in training mode using model.train().
      • Second, make predictions: predictions = model(training_data).
    • Step 2: Calculate the loss.
      • Your model will start off making errors.
      • These errors are the difference between your prediction and the ground truth.
      • You can calculate this as: loss = loss_fxn(predictions, ground_truth).
    • Step 3: Zero gradients.
      • You need to zero out the gradients for the optimizer prior to performing back propagation.
      • If gradients accumulate across iterations, then your model won’t train properly.
      • You can do this via optimizer.zero_grad().
    • Step 4: Backprop.
      • Next, you compute the gradient of the loss with respect to model parameter via backprop.
      • Only parameters with requires_grad = True will be updated.
      • This is where the learning starts to happen.
      • PyTorch makes it easy, all you do is call: loss.backward().
    • Step 5: Update the optimizer (gradient descent).
      • Now it’s time to update your trainable parameters so that you can make better predictions.
      • Remember, trainable means that the parameter has requires_grad=True.
      • To update your parameters, all you do is call: optimizer.step().
    • Putting it all together: 
        for epoch in range(epochs):
  model.train()
  preds = model(X_train)
  loss = loss_fxn(preds, truth)
  optimizer.zero_grad()
  loss.backward()
  optimizer.step()
  • Key takeaways
    • The training process consists of three major components in the following order: opt.zero_grad(), loss.backward() and opt.step().
    • optimizer.zero_grad() clears old gradients from the last step (otherwise you’d just accumulate the gradients from all loss.backward() calls).
    • loss.backward() computes the gradients of the loss w.r.t. the parameters (or any function requiring gradients) using backpropagation. Note that loss.backward() accumulates gradients (by having the model keep track of the previously computed gradient) from all previous calls unless cleared using optimizer.zero_grad().
    • optimizer.step() causes the optimizer to take a step based on the gradients of the parameters (which it access through the gradients stored in model).
  • Next, we’ll cover how to write a simple model in PyTorch, compute the loss and define an optimizer. The subsequent sections each cover a case of fetching data – one for image data and another for text data.

Models in PyTorch

  • A model can be defined in PyTorch by subclassing the torch.nn.Module class. The model is defined using two steps. We first specify the parameters of the model, and then outline how they are applied to the inputs. For operations that do not involve trainable parameters (activation functions such as ReLU, operations like MaxPool), we generally use the torch.nn.functional module.
  • For a visual treatment of how to go about creating neural networks in PyTorch, check out The StatQuest Introduction to PyTorch.
  • Here’s an example of a single hidden layer neural network borrowed from here:
import torch.nn as nn
import torch.nn.functional as F

class TwoLayerNet(nn.Module):
    def __init__(self, D_in, H, D_out):
        """
        In the constructor, we instantiate two nn.Linear modules and assign them as
        member variables.

        D_in: input dimension
        H: dimension of hidden layer
        D_out: output dimension
        """
        super(TwoLayerNet, self).__init__()
        self.linear1 = nn.Linear(D_in, H) 
        self.linear2 = nn.Linear(H, D_out)

    def forward(self, x):
        """
        In the forward function, we accept a Variable of input data and we must 
        return a Variable of output data. We can use Modules defined in the 
        constructor as well as arbitrary operators on Variables.
        """
        h_relu = F.relu(self.linear1(x))
        y_pred = self.linear2(h_relu)
        return y_pred
  • The __init__ function initializes the two linear layers of the model. PyTorch takes care of the proper initialization of the parameters you specify. In the forward function, we first apply the first linear layer, apply ReLU activation and then apply the second linear layer. The module assumes that the first dimension of x is the batch size. If the input to the network is simply a vector of dimension 100, and the batch size is 32, then the dimension of x would be (32, 100). Let’s see an example of how to instantiate a model and compute a forward pass:
# N is batch size; D_in is input dimension;
# H is the dimension of the hidden layer; D_out is output dimension.
N, D_in, H, D_out = 32, 100, 50, 10

# Create random Tensors to hold inputs and outputs, and wrap them in Variables
x = Variable(torch.randn(N, D_in)) # dim: 32 x 100

# Construct our model by instantiating the class defined above
model = TwoLayerNet(D_in, H, D_out)

# Forward pass: Compute predicted y by passing x to the model
y_pred = model(x) # dim: 32 x 10
  • More complex models follow the same layout, and we’ll see two of them in the subsequent posts.

Loss functions

  • PyTorch comes with many standard loss functions available for you to use in the torch.nn module. From the documentation, here’s a gist of what PyTorch has to offer in terms of loss functions:
Loss function Description
nn.L1Loss() Creates a criterion that measures the mean absolute error (MAE) between each element in the input \(x\) and target \(y\).
nn.MSELoss() Creates a criterion that measures the mean squared error (squared L2 norm) between each element in the input \(x\) and target \(y\).
nn.BCELoss() Creates a criterion that measures the Binary Cross Entropy between the target and the output.
nn.BCEWithLogitsLoss() This loss combines a Sigmoid layer and the BCELoss in one single class.
nn.CrossEntropyLoss() This criterion combines nn.LogSoftmax() and nn.NLLLoss() in one single class.
nn.CTCLoss() The Connectionist Temporal Classification loss.
nn.NLLLoss() The negative log likelihood loss.
nn.PoissonNLLLoss() Negative log likelihood loss with Poisson distribution of target.
nn.KLDivLoss() The Kullback-Leibler divergence loss measure.
nn.MarginRankingLoss() Creates a criterion that measures the loss given inputs \(x_1, x_2\), two 1D mini-batch Tensors, and a label 1D mini-batch tensor \(y\) (containing 1 or \(-1)\).
nn.HingeEmbeddingLoss() Measures the loss given an input tensor \(x\) and a labels tensor \(y\) (containing 1 or -1).
nn.MultiLabelMarginLoss() Creates a criterion that optimizes a multi-class multi-classification hinge loss (margin-based loss) between input \(x\) (a 2D mini-batch Tensor) and output yy (which is a 2D Tensor of target class indices).
nn.SmoothL1Loss() Creates a criterion that uses a squared term if the absolute element-wise error falls below 1 and an L1 term otherwise.
nn.SoftMarginLoss() Creates a criterion that optimizes a two-class classification logistic loss between input tensor \(x\) and target tensor \(y\) (containing 1 or \(-1\).
nn.MultiLabelSoftMarginLoss() Creates a criterion that optimizes a multi-label one-versus-all loss based on max-entropy, between input \(x\) and target \(y\) of size \((N, C)\).
nn.CosineEmbeddingLoss() Creates a criterion that measures the loss given input tensors \(x_1, x_2\) and a Tensor label \(y\) with values 1 or \(-1\).
nn.MultiMarginLoss() Creates a criterion that optimizes a multi-class classification hinge loss (margin-based loss) between input \(x\) (a 2D mini-batch Tensor) and output \(y\) (which is a 1D tensor of target class indices, \(0 \leq y \leq \text{x.size}(1)-1\)).
nn.TripletMarginLoss() Creates a criterion that measures the triplet loss given an input tensors \(x_1, x_2, x_3\) and a margin with a value greater than 0.
  • Full API details are on PyTorch’s torch.nn module page.
  • Here’s a simple example of how to calculate Cross Entropy Loss. Let’s say our model solves a multi-class classification problem with \(C\) labels. Then for a batch of size \(N\), out is a PyTorch Variable of dimension \(N \times C\) that is obtained by passing an input batch through the model.
  • We also have a target Variable of size \(N\), where each element is the class for that example, i.e., a label in \(\text{[0, …, C-1]}\). You can define the loss function and compute the loss as follows:
loss_fn = nn.CrossEntropyLoss()
loss = loss_fn(out, target)
  • PyTorch makes it very easy to extend this and write your own custom loss function. We can write our own Cross Entropy Loss function as below (note the NumPy-esque syntax):
def myCrossEntropyLoss(outputs, labels):
    batch_size = outputs.size()[0]               # batch_size
    outputs = F.log_softmax(outputs, dim=1)      # compute the log of softmax values
    outputs = outputs[range(batch_size), labels] # pick the values corresponding to the labels
    return -torch.sum(outputs)/num_examples
  • Note that when training multi-class classifiers in PyTorch, using nn.CrossEntropyLoss(), the input must be an unnormalized raw value (logits), and the target must be a class index instead of one hot encoded vector. On the other hand, when training binary classifiers in PyTorch, make sure to use the correct binary loss for your network structure. BCELoss() accepts the output of the sigmoid function. On the other hand, BCEWithLogitsLoss() improves numeric stability, but make sure you pass the unnormalized logits as an input because it will apply the sigmoid itself. Passing in the sigmoid output will lead to accidentally applying softmax twice, which many people learn the hard way. While it’s not quite clear why the double application of softmax “kills” training, it is likely due to vanishing gradients. To summarize, for binary classification, PyTorch offers nn.BCELoss() and nn.BCEWithLogitsLoss(). The former requires the input normalized sigmoid probability, an the latter can take raw unnormalized logits.

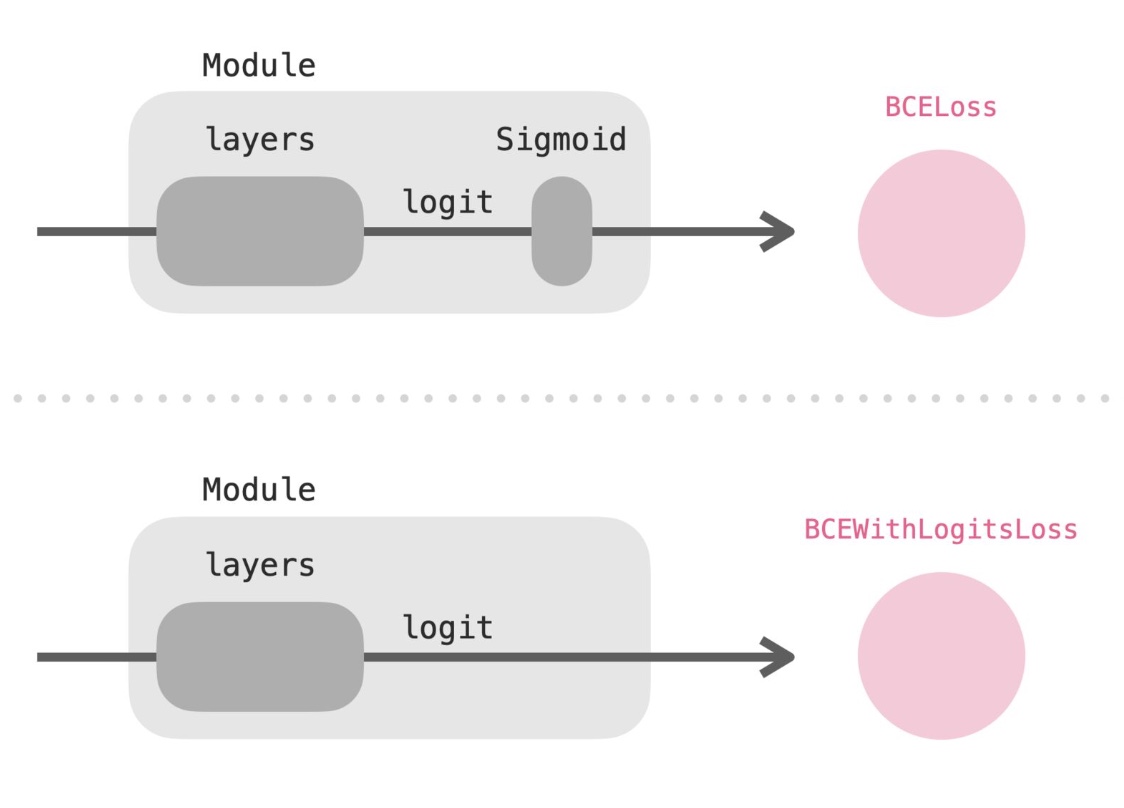
  • This was a fairly trivial example of writing our own loss function. In the section on NLP, we’ll see an interesting use of custom loss functions.

Optimizers

  • The torch.optim package provides an easy to use interface for common optimization algorithms. Torch offers a bunch of in-built optimizers, such as:
Optimizer Description
torch.optim.Adagrad() Proposed in “Adaptive Subgradient Methods for Online Learning and Stochastic Optimization”.
torch.optim.Adadelta() Proposed in “ADADELTA: An Adaptive Learning Rate Method”.
torch.optim.Adam() Proposed in “Adam: A Method for Stochastic Optimization”.
torch.optim.AdamW() A variant of Adam, proposed in “Decoupled Weight Decay Regularization”.
torch.optim.SparseAdam() A lazy version of Adam algorithm suitable for sparse tensors, where only moments that show up in the gradient get updated, and only those portions of the gradient get applied to the parameters.
torch.optim.Adamax() A variant of Adam based on infinity norm, proposed in “Adam: A Method for Stochastic Optimization”.
torch.optim.ASGD() Averaged SGD, proposed in “Acceleration of stochastic approximation by averaging”.
torch.optim.LBFGS() L-BFGS algorithm, heavily inspired by minFunc.
torch.optim.RMSprop() Proposed by G. Hinton in his course. The centered version first appears in “Generating Sequences With Recurrent Neural Networks”.
torch.optim.Rprop() Implements the resilient backpropagation algorithm.
torch.optim.SGD() Implements stochastic gradient descent (optionally with momentum). Nesterov momentum is based on the formula from “On the importance of initialization and momentum in deep learning”.
  • Full API details are on PyTorch’s torch.optim package page.
  • Here’s how you can instantiate your desired optimizer using torch.optim:
# pick an SGD optimizer
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

# or pick ADAM
optimizer = torch.optim.Adam(model.parameters(), lr=0.0001)
  • You pass in the parameters of the model that need to be updated on every iteration. You can also specify more complex methods such as per-layer or even per-parameter learning rates.
  • Once gradients have been computed using loss.backward(), calling optimizer.step() updates the parameters as defined by the optimization algorithm.

Training vs. evaluation

  • Before training the model, it is imperative to call model.train(). Likewise, you must call model.eval() before testing the model.
  • This corrects for the differences in dropout, batch normalization during training and testing.

Computing metrics

  • By this stage you should be able to understand most of the code in train.py and evaluate.py (except how we fetch the data, which we’ll come to in the subsequent posts). Apart from keeping an eye on the loss, it is also helpful to monitor other metrics such as accuracy, precision or recall. To do this, you can define your own metric functions for a batch of model outputs in the model/net.py file.
  • In order to make it easier, we convert the PyTorch Variables into NumPy arrays before passing them into the metric functions.
  • For a multi-class classification problem as set up in the section on loss functions, we can write a function to compute accuracy using NumPy as:
def accuracy(out, labels):
    outputs = np.argmax(out, axis=1)
    return np.sum(outputs==labels)/float(labels.size)
  • You can add your own metrics in the model/net.py file. Once you are done, simply add them to the metrics dictionary:
metrics = { 'accuracy': accuracy,
            # add your own custom metrics,
          }

Saving and loading models

  • We define utility functions to save and load models in utils.py. To save your model, call:
state = {'epoch': epoch + 1,
        'state_dict': model.state_dict(),
        'optim_dict' : optimizer.state_dict()}
utils.save_checkpoint(state,
                      is_best=is_best,      # True if this is the model with best metrics
                      checkpoint=model_dir) # path to folder

  • utils.py internally uses the torch.save(state, filepath) method to save the state dictionary that is defined above. You can add more items to the dictionary, such as metrics. The model.state_dict() stores the parameters of the model and optimizer.state_dict() stores the state of the optimizer (such as per-parameter learning rate).

  • To load the saved state from a checkpoint, you may use:

utils.load_checkpoint(restore_path, model, optimizer)
  • The optimizer argument is optional and you may choose to restart with a new optimizer. load_checkpoint internally loads the saved checkpoint and restores the model weights and the state of the optimizer.

Using the GPU

  • Interspersed through the code, you will find lines such as:
model = net.Net(params).cuda() if params.cuda else net.Net(params)

if params.cuda:
    batch_data, batch_labels = batch_data.cuda(), batch_labels.cuda()
  • PyTorch makes the use of the GPU explicit and transparent using these commands. Calling .cuda() on a model/Tensor/Variable sends it to the GPU. In order to train a model on the GPU, all the relevant parameters and Variables must be sent to the GPU using .cuda().

Painless debugging

  • With its clean and minimal design, PyTorch makes debugging a breeze. You can place breakpoints using import pdb; pdb.set_trace() at any line in your code. You can then execute further computations, examine the PyTorch Tensors/Variables and pinpoint the root cause of the error.

  • That concludes the introduction to the PyTorch code examples. Next, we take upon an example from vision and NLP to understand how we load data and define models specific to each domain.

Vision: Predicting labels from images of hand signs

Goals of this tutorial

  • Learn how to use PyTorch to load image data efficiently.
  • Formulate a convolutional neural network in code.
  • Understand the key aspects of the code well-enough to modify it to suit your needs.

Problem setup

  • We’ll use the SIGNS dataset from deeplearning.ai. The dataset consists of 1080 training images and 120 test images.
  • Each image from this dataset is a picture of a hand making a sign that represents a number between 1 and 6. For our particular use-case, we’ll scale down images to size \(64 \times 64\).

Structure of the dataset

  • For the vision example, we will used the SIGNS dataset created for the Coursera Deep Learning Specialization. The dataset is hosted on google drive, download it here.

  • This will download the SIGNS dataset (~1.1 GB) containing photos of hands signs representing numbers between 0 and 5. Here is the structure of the data:

SIGNS/
    train_signs/
        0_IMG_5864.jpg
        ...
    test_signs/
        0_IMG_5942.jpg
        ...

  • The images are named following {label}_IMG_{id}.jpg where the label is in \(\text{[0, 5]}\).

  • Once the download is complete, move the dataset into the data/SIGNS folder. Run python build_dataset.py which will resize the images to size \((64, 64)\). The new resized dataset will be located by default in data/64x64_SIGNS.

Creating a PyTorch dataset

  • torch.utils.data provides some nifty functionality for loading data. We use torch.utils.data.Dataset, which is an abstract class representing a dataset. To make our own SIGNSDataset class, we need to inherit the Dataset class and override the following methods:
    • __len__: so that len(dataset) returns the size of the dataset
    • __getitem__: to support indexing using dataset[i] to get the ith image
  • We then define our class as below:
from PIL import Image
from torch.utils.data import Dataset, DataLoader

class SIGNSDataset(Dataset):
    def __init__(self, data_dir, transform):      
        # store filenames
        # self.filenames = os.listdir(data_dir) or ...
        self.filenames = [os.path.join(data_dir, f) for f in self.filenames]

    # the first character of the filename contains the label
    self.labels = [int(filename.split('/')[-1][0]) for filename in self.filenames]
    self.transform = transform

def __len__(self):
    # return size of dataset
    return len(self.filenames)

def __getitem__(self, idx):
    # open image, apply transforms and return with label
    image = Image.open(self.filenames[idx])  # PIL image
    image = self.transform(image)
    return image, self.labels[idx]
  • Notice that when we return an image-label pair using __getitem__ we apply a transform on the image. These transformations are a part of the torchvision.transforms package, that allow us to manipulate images easily. Consider the following composition of multiple transforms:
train_transformer = transforms.Compose([
    transforms.Resize(64),              # resize the image to 64x64 
    transforms.RandomHorizontalFlip(),  # randomly flip image horizontally
    transforms.ToTensor()])             # transform it into a PyTorch Tensor
  • When we apply self.transform(image) in __getitem__, we pass it through the above transformations before using it as a training example. The final output is a PyTorch Tensor. To augment the dataset during training, we also use the RandomHorizontalFlip transform when loading the image.
  • We can specify a similar eval_transformer for evaluation without the random flip. To load a Dataset object for the different splits of our data, we simply use:
train_dataset = SIGNSDataset(train_data_path, train_transformer)
val_dataset = SIGNSDataset(val_data_path, eval_transformer)
test_dataset = SIGNSDataset(test_data_path, eval_transformer)

Loading data batches

  • torch.utils.data.DataLoader provides an iterator that takes in a Dataset object and performs batching, shuffling and loading of the data. This is crucial when images are big in size and take time to load. In such cases, the GPU can be left idling while the CPU fetches the images from file and then applies the transforms.
  • In contrast, the DataLoader class (using multiprocessing) fetches the data asynchronously and prefetches batches to be sent to the GPU. Initializing the DataLoader is quite easy:
train_dataloader = DataLoader(SIGNSDataset(train_data_path, train_transformer), 
                   batch_size=hyperparams.batch_size, shuffle=True,
                   num_workers=hyperparams.num_workers)
  • We can then iterate through batches of examples as follows:
for train_batch, labels_batch in train_dataloader:
    # wrap Tensors in Variables
    train_batch, labels_batch = Variable(train_batch), Variable(labels_batch)

    # pass through model, perform backpropagation and updates
    output_batch = model(train_batch)
    ...
  • Applying transformations on the data loads them as PyTorch Tensors. We wrap them in PyTorch Variables before passing them into the model. The for loop ends after one pass over the data, i.e., after one epoch. It can be reused again for another epoch without any changes. We can use similar data loaders for validation and test data.
  • To read more on splitting the dataset into train/dev/test, see our tutorial on splitting datasets.

Convolutional network model

  • Now that we’ve figured out how to load our images, let’s have a look at the pièce de résistance – the CNN model. As mentioned in the section on tensors and variables, we first define the components of our model, followed by its functional form. Let’s have a look at the __init__ function for our model that takes in a \(3 \times 64 \times 64\) image:
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        # we define convolutional layers 
        self.conv1 = nn.Conv2d(in_channels = 3, out_channels = 32, kernel_size = 3, stride = 1, padding = 1)
        self.bn1 = nn.BatchNorm2d(32)
        self.conv2 = nn.Conv2d(in_channels = 32, out_channels = 64, kernel_size = 3, stride = 1, padding = 1)
        self.bn2 = nn.BatchNorm2d(64)
        self.conv3 = nn.Conv2d(in_channels = 64, in_channels = 128, kernel_size = 3, stride = 1, padding = 1)
        self.bn3 = nn.BatchNorm2d(128)

        # 2 fully connected layers to transform the output of the convolution layers to the final output
        self.fc1 = nn.Linear(in_features = 8*8*128, out_features = 128)
        self.fcbn1 = nn.BatchNorm1d(128)
        self.fc2 = nn.Linear(in_features = 128, out_features = 6)       
        self.dropout_rate = hyperparams.dropout_rate

  • The first parameter to the convolutional filter nn.Conv2d is the number of input channels, the second is the number of output channels, and the third is the size of the square filter (\(3 \times 3\) in this case). Similarly, the batch normalization layer takes as input the number of channels for 2D images and the number of features in the 1D case. The fully connected Linear layers take the input and output dimensions.

  • In this example, we explicitly specify each of the values. In order to make the initialization of the model more flexible, you can pass in parameters such as image size to the __init__ function and use that to specify the sizes. You must be very careful when specifying parameter dimensions, since mismatches will lead to errors in the forward propagation. Let’s now look at the forward propagation:

def forward(self, s):
    # We apply the convolution layers, followed by batch normalisation, 
    # MaxPool and ReLU x 3
    s = self.bn1(self.conv1(s))        # batch_size x 32 x 64 x 64
    s = F.relu(F.max_pool2d(s, 2))     # batch_size x 32 x 32 x 32
    s = self.bn2(self.conv2(s))        # batch_size x 64 x 32 x 32
    s = F.relu(F.max_pool2d(s, 2))     # batch_size x 64 x 16 x 16
    s = self.bn3(self.conv3(s))        # batch_size x 128 x 16 x 16
    s = F.relu(F.max_pool2d(s, 2))     # batch_size x 128 x 8 x 8

    # Flatten the output for each image
    s = s.view(-1, 8*8*128)  # batch_size x 8*8*128

    # Apply 2 fully connected layers with dropout
    s = F.dropout(F.relu(self.fcbn1(self.fc1(s))), 
    p = self.dropout_rate, training=self.training)    # batch_size x 128
    s = self.fc2(s)                                     # batch_size x 6

    return F.log_softmax(s, dim=1)

  • We pass the image through 3 layers of conv > bn > max_pool > relu, followed by flattening the image and then applying 2 fully connected layers. In flattening the output of the convolution layers to a single vector per image, we use s.view(-1, 8*8*128). Here the size -1 is implicitly inferred from the other dimension (batch size in this case). The output is a log_softmax over the 6 labels for each example in the batch. We use log_softmax since it is numerically more stable than first taking the softmax and then the log.

  • And that’s it! We use an appropriate loss function (Negative Loss Likelihood, since the output is already softmax-ed and log-ed) and train the model as discussed in the previous post. Remember, you can set a breakpoint using import pdb; pdb.set_trace() at any place in the forward function, examine the dimensions of variables, tinker around and diagnose what’s wrong. That’s the beauty of PyTorch :).

Resources

NLP: Named Entity Recognition (NER) tagging

Goals of this tutorial

  • Learn how to use PyTorch to load sequential data.
  • Define a recurrent neural network that operates on text (or more generally, sequential data).
  • Understand the key aspects of the code well-enough to modify it to suit your needs

Problem setup

  • We explore the problem of Named Entity Recognition (NER) tagging of sentences.
  • The task is to tag each token in a given sentence with an appropriate tag such as Person, Location, etc.
John   lives in New   York
B-PER  O     O  B-LOC I-LOC
  • Our dataset will thus need to load both the sentences and labels. We will store those in 2 different files, a sentence.txt file containing the sentences (one per line) and a labels.txt containing the labels. For example:
# sentences.txt
John lives in New York
Where is John ?

# labels.txt
B-PER O O B-LOC I-LOC
O O B-PER O
  • Here we assume that we ran the build_vocab.py script that creates a vocabulary file in our /data directory. Running the script gives us one file for the words and one file for the labels. They will contain one token per line. For instance,
# words.txt
John
lives
in
...

and

#tags.txt
B-PER
B-LOC
...

Structure of the dataset

  • Download the original version on the Kaggle website.

  • Download the dataset: ner_dataset.csv on Kaggle and save it under the nlp/data/kaggle directory. Make sure you download the simple version ner_dataset.csv and NOT the full version ner.csv.

  • Build the dataset: Run the following script:

python build_kaggle_dataset.py
  • It will extract the sentences and labels from the dataset, split it into train / test / dev and save it in a convenient format for our model. Here is the structure of the data
kaggle/
    train/
        sentences.txt
        labels.txt
    test/
        sentences.txt
        labels.txt
    dev/
        sentences.txt
        labels.txt

  • If this errors out, check that you downloaded the right file and saved it in the right directory. If you have issues with encoding, try running the script with Python 2.7.

  • Build the vocabulary: For both datasets, data/small and data/kaggle you need to build the vocabulary, with:

python build_vocab.py --data_dir  data/small

or

python build_vocab.py --data_dir data/kaggle

Loading text data

  • In NLP applications, a sentence is represented by the sequence of indices of the words in the sentence. For example if our vocabulary is {'is':1, 'John':2, 'Where':3, '.':4, '?':5} then the sentence “Where is John ?” is represented as [3,1,2,5]. We read the words.txt file and populate our vocabulary:
vocab = {}
with open(words_path) as f:
    for i, l in enumerate(f.read().splitlines()):
        vocab[l] = i

  • In a similar way, we load a mapping tag_map from our labels from tags.txt to indices. Doing so gives us indices for labels in the range \(\text{[0, 1, …, NUM_TAGS-1]}\).

  • In addition to words read from English sentences, words.txt contains two special tokens: an UNK token to represent any word that is not present in the vocabulary, and a PAD token that is used as a filler token at the end of a sentence when one batch has sentences of unequal lengths.

  • We are now ready to load our data. We read the sentences in our dataset (either train, validation or test) and convert them to a sequence of indices by looking up the vocabulary:

train_sentences = []        
train_labels = []

with open(train_sentences_file) as f:
    for sentence in f.read().splitlines():
        # replace each token by its index if it is in vocab
        # else use index of UNK
        s = [vocab[token] if token in self.vocab 
            else vocab['UNK']
            for token in sentence.split(' ')]
        train_sentences.append(s)

with open(train_labels_file) as f:
    for sentence in f.read().splitlines():
        # replace each label by its index
        l = [tag_map[label] for label in sentence.split(' ')]
        train_labels.append(l)
  • We can load the validation and test data in a similar fashion.

Preparing a Batch

  • This is where it gets fun. When we sample a batch of sentences, not all the sentences usually have the same length. Let’s say we have a batch of sentences batch_sentences that is a Python list of lists, with its corresponding batch_tags which has a tag for each token in batch_sentences. We convert them into a batch of PyTorch Variables as follows:
# compute length of longest sentence in batch
batch_max_len = max([len(s) for s in batch_sentences])

# prepare a numpy array with the data, initializing the data with 'PAD' 
# and all labels with -1; initializing labels to -1 differentiates tokens 
# with tags from 'PAD' tokens
batch_data = vocab['PAD']*np.ones((len(batch_sentences), batch_max_len))
batch_labels = -1*np.ones((len(batch_sentences), batch_max_len))

# copy the data to the numpy array
for j in range(len(batch_sentences)):
    cur_len = len(batch_sentences[j])
    batch_data[j][:cur_len] = batch_sentences[j]
    batch_labels[j][:cur_len] = batch_tags[j]

# since all data are indices, we convert them to torch LongTensors
batch_data, batch_labels = torch.LongTensor(batch_data), torch.LongTensor(batch_labels)

# convert Tensors to Variables
batch_data, batch_labels = Variable(batch_data), Variable(batch_labels)
  • A lot of things happened in the above code. We first calculated the length of the longest sentence in the batch. We then initialized NumPy arrays of dimension (num_sentences, batch_max_len) for the sentence and labels, and filled them in from the lists.

  • Since the values are indices (and not floats), PyTorch’s Embedding layer expects inputs to be of the Long type. We hence convert them to LongTensor.

  • After filling them in, we observe that the sentences that are shorter than the longest sentence in the batch have the special token PAD to fill in the remaining space. Moreover, the PAD tokens, introduced as a result of packaging the sentences in a matrix, are assigned a label of -1. Doing so differentiates them from other tokens that have label indices in the range \(\text{[0, 1, …, NUM_TAGS-1]}\). This will be crucial when we calculate the loss for our model’s prediction, and we’ll come to that in a bit.

  • In our code, we package the above code in a custom data_iterator function. Hyperparameters are stored in a data structure called “params”. We can then use the generator as follows:
# train_data contains train_sentences and train_labels
# params contains batch_size
train_iterator = data_iterator(train_data, params, shuffle=True)    

for _ in range(num_training_steps):
    batch_sentences, batch_labels = next(train_iterator)

    # pass through model, perform backpropagation and updates
    output_batch = model(train_batch)
    ...

Recurrent network model

  • Now that we have figured out how to load our sentences and tags, let’s have a look at the Recurrent Neural Network model. As mentioned in the section on tensors and variables, we first define the components of our model, followed by its functional form. Let’s have a look at the __init__ function for our model that takes in (batch_size, batch_max_len) dimensional data:
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self, params):
        super(Net, self).__init__()

    # maps each token to an embedding_dim vector
    self.embedding = nn.Embedding(params.vocab_size, params.embedding_dim)

    # the LSTM takens embedded sentence
    self.lstm = nn.LSTM(params.embedding_dim, params.lstm_hidden_dim, batch_first=True)

    # FC layer transforms the output to give the final output layer
    self.fc = nn.Linear(params.lstm_hidden_dim, params.number_of_tags)
  • We use an LSTM for the recurrent network. Before running the LSTM, we first transform each word in our sentence to a vector of dimension embedding_dim. We then run the LSTM over this sentence. Finally, we have a fully connected layer that transforms the output of the LSTM for each token to a distribution over tags. This is implemented in the forward propagation function:
def forward(self, s):
    # apply the embedding layer that maps each token to its embedding
    s = self.embedding(s)   # dim: batch_size x batch_max_len x embedding_dim

    # run the LSTM along the sentences of length batch_max_len
    s, _ = self.lstm(s)     # dim: batch_size x batch_max_len x lstm_hidden_dim                

    # reshape the Variable so that each row contains one token
    s = s.view(-1, s.shape[2])  # dim: batch_size*batch_max_len x lstm_hidden_dim

    # apply the fully connected layer and obtain the output for each token
    s = self.fc(s)          # dim: batch_size*batch_max_len x num_tags

    return F.log_softmax(s, dim=1)   # dim: batch_size*batch_max_len x num_tags

  • The embedding layer augments an extra dimension to our input which then has shape (batch_size, batch_max_len, embedding_dim). We run it through the LSTM which gives an output for each token of length lstm_hidden_dim. In the next step, we open up the 3D Variable and reshape it such that we get the hidden state for each token, i.e., the new dimension is (batch_size*batch_max_len, lstm_hidden_dim). Here the -1 is implicitly inferred to be equal to batch_size*batch_max_len. The reason behind this reshaping is that the fully connected layer assumes a 2D input, with one example along each row.

  • After the reshaping, we apply the fully connected layer which gives a vector of NUM_TAGS for each token in each sentence. The output is a log_softmax over the tags for each token. We use log_softmax since it is numerically more stable than first taking the softmax and then the log.

  • All that is left is to compute the loss. But there’s a catch - we can’t use a torch.nn.loss function straight out of the box because that would add the loss from the PAD tokens as well. Here’s where the power of PyTorch comes into play - we can write our own custom loss function!

Writing a custom loss function

  • In the section on loading data batches, we ensured that the labels for the PAD tokens were set to -1. We can leverage this to filter out the PAD tokens when we compute the loss. Let us see how:
def loss_fn(outputs, labels):
    # reshape labels to give a flat vector of length batch_size*seq_len
    labels = labels.view(-1)  

    # mask out 'PAD' tokens
    mask = (labels >= 0).float()

    # the number of tokens is the sum of elements in mask
    num_tokens = int(torch.sum(mask).data[0])

    # pick the values corresponding to labels and multiply by mask
    outputs = outputs[range(outputs.shape[0]), labels]*mask

    # cross entropy loss for all non 'PAD' tokens
    return -torch.sum(outputs)/num_tokens

  • The input labels has dimension (batch_size, batch_max_len) while outputs has dimension (batch_size*batch_max_len, NUM_TAGS). We compute a mask using the fact that all PAD tokens in labels have the value -1. We then compute the Negative Log Likelihood Loss (remember the output from the network is already softmax-ed and log-ed!) for all the non PAD tokens. We can now compute derivates by simply calling .backward() on the loss returned by this function.

  • Remember, you can set a breakpoint using import pdb; pdb.set_trace() at any place in the forward function, loss function or virtually anywhere and examine the dimensions of the Variables, tinker around and diagnose what’s wrong. That’s the beauty of PyTorch :).

Selected methods

  • PyTorch provides a host of useful functions for performing computations on arrays. Below, we’ve touched upon some of the most useful ones that you’ll encounter regularly in projects.
  • You can find an exhaustive list of mathematical functions in the PyTorch documentation.

Tensor shape/size

  • Unlike [NumPy], where size() returns the total number of elements in the array across all dimensions, size() in PyTorch returns the shape of an array.
import torch

a = torch.randn(2, 3, 5)

# Get the overall shape of the tensor
a.size()   # Prints torch.Size([2, 3, 5])
a.shape    # Prints torch.Size([2, 3, 5])

# Get the size of a specific axis/dimension of the tensor
a.size(2)  # Prints 5
a.shape[2] # Prints 5

Initialization

  • Presented below are some commonly used initialization functions. A full list can be found on the PyTorch documentation’s torch.nn.init page.

Static

  • torch.nn.init.zeros_() fills the input Tensor with the scalar value 0.
  • torch.nn.init.ones_() fills the input Tensor with the scalar value 1.
  • torch.nn.init.constant_() fills the input Tensor with the passed in scalar value.
import torch.nn as nn

a = torch.empty(3, 5)
nn.init.zeros_(a)         # Initializes a with 0
nn.init.ones_(a)          # Initializes a with 1
nn.init.constant_(a, 0.3) # Initializes a with 0.3

Standard normal

  • Returns a tensor filled with random numbers from a normal distribution with mean 0 and variance 1 (also called the standard normal distribution).
\[\text{out}_{i} \sim \mathcal{N}(0, 1)\] 
import torch

torch.randn(4)    # Returns 4 values from the standard normal distribution
torch.randn(2, 3) # Returns a 2x3 matrix sampled from the standard normal distribution

Xavier/Glorot

Uniform
  • Fills the input Tensor with values according to the method described in Understanding the difficulty of training deep feed-forward neural networks - Glorot, X. & Bengio, Y. (2010), using a uniform distribution. The resulting tensor will have values sampled from \(\mathcal{U}(-a, a)\) where,
\[a = \text{gain} \times \sqrt{\frac{6}{\text{fan_in} + \text{fan_out}}}\]
  • Also known as Glorot initialization.
import torch.nn as nn

a = torch.empty(3, 5)
nn.init.xavier_uniform_(a, gain=nn.init.calculate_gain('relu')) # Initializes a with the Xavier uniform method
Normal
  • Fills the input Tensor with values according to the method described in Understanding the difficulty of training deep feed-forward neural networks - Glorot, X. & Bengio, Y. (2010), using a normal distribution. The resulting tensor will have values sampled from \(\mathcal{N}(0, \text{std}^2)\) where,
\[\text{std} = \text{gain} \times \sqrt{\frac{2}{\text{fan_in} + \text{fan_out}}}\]
  • Also known as Glorot initialization.
import torch.nn as nn

a = torch.empty(3, 5)
nn.init.xavier_normal_(a) # Initializes a with the Xavier normal method

Kaiming/He

Uniform
  • Fills the input Tensor with values according to the method described in Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification - He, K. et al. (2015), using a uniform distribution. The resulting tensor will have values sampled from \(\mathcal{U}(-\text{bound}, \text{bound})\) where,
\[\text{bound} = \text{gain} \times \sqrt{\frac{3}{\text{fan_mode}}}\]
  • Also known as He initialization.
import torch.nn as nn

a = torch.empty(3, 5)
nn.init.kaiming_uniform_(a, mode='fan_in', nonlinearity='relu') # Initializes a with the Kaiming uniform method
Normal
  • Fills the input Tensor with values according to the method described in Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification - He, K. et al. (2015), using a normal distribution. The resulting tensor will have values sampled from \(\mathcal{N}(0, \text{std}^2)\) where,
\[\operatorname{std}=\frac{\text { gain }}{\sqrt{\text { fan_mode }}}\]
  • Also known as He initialization.
import torch.nn as nn

a = torch.empty(3, 5)
nn.init.kaiming_normal_(a, mode='fan_out', nonlinearity='relu') # Initializes a with the Kaiming uniform method

Send Tensor to GPU

  • To send a tensor (or model) to the GPU, you may use tensor.cuda() or tensor.to(device):
import torch

t = torch.tensor([1, 2, 3])
a = t.cuda()
type(a) # Prints <class 'numpy.ndarray'>

# Send tensor to the GPU
a = a.cuda()

# Bring the tensor back to the CPU
a = a.cpu()
  • Note that there is no difference between the two. Early versions of PyTorch had tensor.cuda() and tensor.cpu() methods to move tensors and models from CPU to GPU and back. However, this made code writing a bit cumbersome:
if cuda_available:
    x = x.cuda()
    model.cuda()
else:
    x = x.cpu()
    model.cpu()
  • Later versions of PyTorch introduced tensor.to() that basically takes care of everything in an elegant way:
device = torch.device('cuda') if cuda_available else torch.device('cpu')
x = x.to(device)
model = model.to(device)

Convert to NumPy

  • Both in PyTorch and TensorFlow, the tensor.numpy() method is pretty much straightforward. It converts a tensor object into an numpy.ndarray object. This implicitly means that the converted tensor will be now processed on the CPU.
import torch

t = torch.tensor([1, 2, 3])
a = t.numpy()               # array([1, 2, 3])
type(a)                     # Prints <class 'numpy.ndarray'>

# Send tensor to the GPU.
t = t.cuda()

b = t.cpu().numpy()          # array([1, 2, 3])
type(b)                      # <class 'numpy.ndarray'>
  • If you originally created a PyTorch Tensor with requires_grad=True (note that requires_grad defaults to False, unless wrapped in a nn.Parameter()), you’ll have to use detach() to get rid of the gradients when sending it downstream for say, post-processing with NumPy, or plotting with Matplotlib/Seaborn. Calling detach() before cpu() prevents superfluous gradient copying. This greatly optimizes runtime. Note that detach() is not necessary if requires_grad is set to False when defining the tensor.
import torch

t = torch.tensor([1, 2, 3], requires_grad=True)
a = t.detach().numpy()       # array([1, 2, 3])
type(a)                      # Prints <class 'numpy.ndarray'>

# Send tensor to the GPU.
t = t.cuda()

# The output of the line below is a NumPy array.
b = t.detach().cpu().numpy() # array([1, 2, 3])
type(b)                      # <class 'numpy.ndarray'>

tensor.item(): Convert Single Value Tensor to Scalar

  • Returns the value of a tensor as a Python int/float. This only works for tensors with one element. For other cases, see [tolist()](#tensortolist-convert-multi-value-tensor-to-scalar).
  • Note that this operation is not differentiable.
import torch

a = torch.tensor([1.0])
a.item()   # Prints 1.0

a.tolist() # Prints [1.0]

tensor.tolist(): Convert Multi Value Tensor to Scalar

  • Returns the tensor as a (nested) list. For scalars, a standard Python number is returned, just like with [item()](#tensoritem-convert-single-value-tensor-to-scalar). Tensors are automatically moved to the CPU first if necessary.
  • Note that this operation is not differentiable.
a = torch.randn(2, 2)
a.tolist()      # Prints [[0.012766935862600803, 0.5415473580360413],
                #         [-0.08909505605697632, 0.7729271650314331]]
a[0,0].tolist() # Prints 0.012766935862600803

Len

  • len() returns the size of the first dimension of the input tensor, similar to NumPy.
import torch

a = torch.Tensor([[1, 2], [3, 4]])
print(a) # Prints tensor([[1., 2.],
         #                [3., 4.]])
len(a)   # 2

b = torch.Tensor([1, 2, 3, 4])
print(b) # Prints tensor([1., 2., 3., 4.])
len(b)   # 4

Arange

  • Return evenly spaced values within the half-open interval \([start, stop)\) (in other words, the interval including start but excluding stop).
  • For integer arguments the function is equivalent to the Python built-in range function, but returns an tensor rather than a list.
import torch

print(torch.arange(8))             # Prints tensor([0 1 2 3 4 5 6 7])
print(torch.arange(3, 8))          # Prints tensor([3 4 5 6 7])
print(torch.arange(3, 8, 2))       # Prints tensor([3 5 7])

# arange() works with floats too (but read the disclaimer below)
print(torch.arange(0.1, 0.5, 0.1)) # Prints tensor([0.1000, 0.2000, 0.3000, 0.4000])
  • When using a non-integer step, such as \(0.1\), the results will often not be consistent. It is better to use torch.linspace() for those cases as below.

Linspace

  • Return evenly spaced numbers calculated over the interval \([start, stop]\).
  • Starting PyTorch 1.11, linspace requires the steps argument. Use steps=100 to restore the previous behavior.
import torch

print(torch.linspace(1.0, 2.0, steps=5)) # Prints tensor([1.0000, 1.2500, 1.5000, 1.7500, 2.0000])

View

  • Returns a new tensor with the same data as the input tensor but of a different shape.
  • For a tensor to be viewed, the following conditions must be satisfied:
    • The new view size must be compatible with its original size and stride, i.e., each new view dimension must either be a subspace of an original dimension, or only span across original dimensions.
    • view() can be only be performed on contiguous tensors (which can be ascertained using is_contiguous()). Otherwise, a contiguous copy of the tensor (e.g., via contiguous()) needs to be used. When it is unclear whether a view() can be performed, it is advisable to use (reshape())[#reshape], which returns a view if the shapes are compatible, and copies the tensor (equivalent to calling contiguous()) otherwise.
import torch

a = torch.arange(4).view(2, 2)

print(a.view(4, 1)) # Prints tensor([[0],
                    #                [1],
                    #                [2],
                    #                [3]])

print(a.view(1, 4)) # Prints tensor([[0, 1, 2, 3]])
  • Passing in a -1 to torch.view() returns a flattened version of the array.
import torch

a = torch.arange(4).view(2, 2)
print(a.view(-1)) # Prints tensor([0, 1, 2, 3])
  • The view tensor shares the same underlying data storage with its base tensor. No data movement occurs when creating a view, view tensor just changes the way it interprets the same data. This avoids explicit data copy, thus allowing fast and memory efficient reshaping, slicing and element-wise operations.
import torch

a = torch.rand(4, 4)
b = a.view(2, 8)
a.storage().data_ptr() == b.storage().data_ptr() # Prints True since `a` and `b` share the same underlying data.
  • Note that modifying the view tensor changes the input tensor as well.
import torch

a = torch.rand(4, 4)
b = a.view(2, 8)
b[0][0] = 3.14

print(t[0][0]) # Prints tensor(3.14)

Transpose

  • Returns a tensor that is a transposed version of input for 2D tensors. More generally, interchanges two axes of an array. In other words, the given dimensions dim0 and dim1 are swapped.
  • The resulting out tensor shares its underlying storage with the input tensor, so changing the content of one would change the content of the other.
import torch

a = torch.randn(2, 3, 5)
a.size()                 # Prints torch.Size([2, 3, 5])

a.transpose(0, -1).shape # Prints torch.Size([5, 3, 2])

Swapaxes

  • Alias for torch.transpose(). This function is equivalent to NumPy’s (swapaxes)[../numpy/#swapaxes] function.
import torch

a = torch.randn(2, 3, 5)
a.size()                # Prints torch.Size([2, 3, 5])

a.swapdims(0, -1).shape # Prints torch.Size([5, 3, 2])

# swapaxes is an alias of swapdims
a.swapaxes(0, -1).shape # Prints torch.Size([5, 3, 2])

Permute

  • Returns a view of the input tensor with its axes ordered as indicated in the input argument.
import torch

a = torch.randn(2, 3, 5)
a.size()                  # Prints torch.Size([2, 3, 5])

a.permute(2, 0, 1).size() # Prints torch.Size([5, 2, 3])
  • Note that (i) using view or reshape to restructure the array, and (ii) permute or transpose to swap axes, can render the same output shape but does not necessarily yield the same tensor in both cases.
a = torch.tensor([[1, 2, 3], [4, 5, 6]])

viewed = a.view(3, 2)
perm = a.permute(1, 0)

viewed.shape   # Prints torch.Size([3, 2])
perm.shape     # Prints torch.Size([3, 2])

viewed == perm # Prints tensor([[ True, False],
               #                [False, False],
               #                [False,  True]])

viewed         # Prints tensor([[1, 2],
               #                [3, 4],
               #                [5, 6]])

perm           # Prints tensor([[1, 4],
               #                [2, 5],
               #                [3, 6]])

Movedim

  • Compared to torch.permute() for reordering axes which needs positions of all axes to be explicitly specified, moving one axis while keeping the relative positions of all others is a common enough use-case to warrant its own syntactic sugar. This is the functionality that is offered by torch.movedim().
import torch

a = torch.randn(2, 3, 5)
a.size()                # Prints torch.Size([2, 3, 5])

a.movedim(0, -1).shape  # Prints torch.Size([3, 5, 2])

# moveaxis is an alias of movedim
a.moveaxis(0, -1).shape # Prints torch.Size([3, 5, 2])

Randperm

  • Returns a random permutation of integers from 0 to n - 1.
import torch

torch.randperm(n=4) # Prints tensor([2, 1, 0, 3])
  • As a practical use-case, torch.randperm() helps select mini-batches containing data samples randomly as follows:
data[torch.randperm(data.shape[0])] # Assuming the first dimension of data is the minibatch number

Where

  • Returns a tensor of elements selected from either a or b, depending on the outcome of the specified condition.
  • The operation is defined as:
\[\text{out}_i = \begin{cases} \text{x}_i & \text{if } \text{condition}_i \\ \text{y}_i & \text{otherwise} \\ \end{cases}\] 
import torch

a = torch.randn(3, 2) # Initializes a as a 3x2 matrix using the the standard normal distribution
b = torch.ones(3, 2)
>>> a
tensor([[-0.4620,  0.3139],
        [ 0.3898, -0.7197],
        [ 0.0478, -0.1657]])
>>> torch.where(a > 0, a, b)
tensor([[ 1.0000,  0.3139],
        [ 0.3898,  1.0000],
        [ 0.0478,  1.0000]])
>>> a = torch.randn(2, 2, dtype=torch.double)
>>> a
tensor([[ 1.0779,  0.0383],
        [-0.8785, -1.1089]], dtype=torch.float64)
>>> torch.where(a > 0, a, 0.)
tensor([[1.0779, 0.0383],
        [0.0000, 0.0000]], dtype=torch.float64)

Reshape

  • Returns a tensor with the same data and number of elements as the input, but with the specified shape. When possible, the returned tensor will be a view of the input. Otherwise, it will be a copy. Contiguous inputs and inputs with compatible strides can be reshaped without copying, but you should not depend on the copying vs. viewing behavior. It means that torch.reshape may return a copy or a view of the original tensor.
  • A single dimension may be -1, in which case it’s inferred from the remaining dimensions and the number of elements in input.
import torch

a = torch.arange(4*10*2).view(4, 10, 2)
b = x.permute(2, 0, 1)

# Reshape works on non-contiguous tensors (contiguous() + view())
print(b.is_contiguous())
try: 
    print(b.view(-1))
except RuntimeError as e:
    print(e)
print(b.reshape(-1))
print(b.contiguous().view(-1))
  • While torch.view() has existed for a long time, torch.reshape() has been recently introduced in PyTorch 0.4. When it is unclear whether a view() can be performed, it is advisable to use reshape(), which returns a view if the shapes are compatible, and copies (equivalent to calling contiguous()) otherwise.

Concatenate

  • Concatenates the input sequence of tensors in the given dimension. All tensors must either have the same shape (except in the concatenating dimension) or be empty.
import torch

x = torch.randn(2, 3)
print(x) # Prints a 2x3 matrix: [[ 0.6580, -1.0969, -0.4614],
         #                       [-0.1034, -0.5790,  0.1497]]

print(torch.cat((x, x, x), 0)) # Prints a 6x3 matrix: [[ 0.6580, -1.0969, -0.4614],
                               #                       [-0.1034, -0.5790,  0.1497],
                               #                       [ 0.6580, -1.0969, -0.4614],
                               #                       [-0.1034, -0.5790,  0.1497],
                               #                       [ 0.6580, -1.0969, -0.4614],
                               #                       [-0.1034, -0.5790,  0.1497]]

print(torch.cat((x, x, x), 1)) # Prints a 2x9 matrix: [[ 0.6580, -1.0969, -0.4614,  
                               #                         0.6580, -1.0969, -0.4614,  
                               #                         0.6580, -1.0969, -0.4614],
                               #                       [-0.1034, -0.5790,  0.1497, 
                               #                        -0.1034, -0.5790,  0.1497, 
                               #                        -0.1034, -0.5790,  0.1497]]

Squeeze

  • Similar to NumPy’s np.squeeze(), torch.squeeze() removes all dimensions with size one from the input tensor. The returned tensor shares the same underlying data with this tensor.

  • For example, if the input is of shape: \((A \times 1 \times B \times C \times 1 \times D)\) then the output tensor will be of shape: \((A \times B \times C \times D)\).

  • When an optional dim argument is given to torch.squeeze(), a squeeze operation is done only in the given dimension. If the input is of shape: \((A \times 1 \times B)\), torch.squeeze(input, 0) leaves the tensor unchanged, but torch.squeeze(input, 1) will squeeze the tensor to the shape \((A \times B)\).

  • An important bit to note is that if the tensor has a batch dimension of size 1, then torch.squeeze() will also remove the batch dimension, which can lead to unexpected errors.

  • Here is a visual representation of what torch.squeeze() and torch.unsqueeze() do for a 2D matrix:

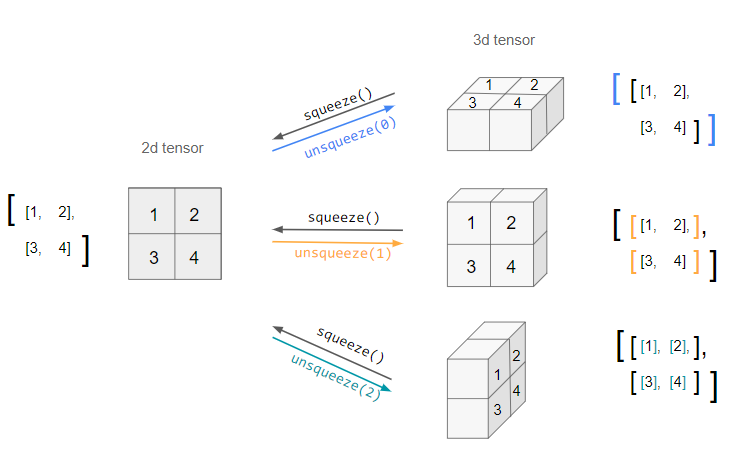
import torch

a = torch.zeros(2, 1, 2, 1, 2)
print(a.size()) # Prints torch.Size([2, 1, 2, 1, 2])

b = torch.squeeze(a)
print(b.size()) # Prints torch.Size([2, 2, 2])

b = torch.squeeze(a, 0)
print(b.size()) # Prints torch.Size([2, 1, 2, 1, 2])

b = torch.squeeze(a, 1)
print(b.size()) # Prints torch.Size([2, 2, 1, 2])

Unsqueeze

  • torch.unsqueeze() is the opposite of torch.squeeze(). It inserts a dimension of size one at the specified position. The returned tensor shares the same underlying data with this tensor.

  • A dim argument within the range [-input.dim() - 1, input.dim() + 1) can be used. A negative value of dim will correspond to torch.unsqueeze() applied at dim = dim + input.dim() + 1.

import torch

a = torch.tensor([1, 2, 3, 4])
print(x.size()) # Prints torch.Size([4])

b = torch.unsqueeze(a, 0) 
print(b)        # Prints tensor([[1, 2, 3, 4]])
print(b.size()) # Prints torch.Size([1, 4])

b = torch.unsqueeze(a, 1)
print(b)        # Prints tensor([[1],
                #                [2],
                #                [3],
                #                [4]])
print(b.size()) # torch.Size([4, 1])

  • Note that unlike torch.squeeze(), the dim argument is required (and not optional) with torch.unsqueeze().

  • A practical use-case of torch.unsqueeze() is to add an additional dimension (usually the first dimension) for the batch number as shown in the example below:

import torch

# 3 channels, 32 width, 32 height
a = torch.randn(3, 32, 32)

# 1 batch, 3 channels, 32 width, 32 height
a.unsqueeze(dim=0).shape
  • Printing the model prints a summary of the model including the different layers involved and their specifications.
from torchvision import models
model = models.vgg16()
print(model)
  • The output in this case would be something as follows:
VGG (
  (features): Sequential (
    (0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): ReLU (inplace)
    (2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (3): ReLU (inplace)
    (4): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
    (5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (6): ReLU (inplace)
    (7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (8): ReLU (inplace)
    (9): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
    (10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (11): ReLU (inplace)
    (12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (13): ReLU (inplace)
    (14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (15): ReLU (inplace)
    (16): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
    (17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (18): ReLU (inplace)
    (19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (20): ReLU (inplace)
    (21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (22): ReLU (inplace)
    (23): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
    (24): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (25): ReLU (inplace)
    (26): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (27): ReLU (inplace)
    (28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (29): ReLU (inplace)
    (30): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
  )
  (classifier): Sequential (
    (0): Dropout (p = 0.5)
    (1): Linear (25088 -> 4096)
    (2): ReLU (inplace)
    (3): Dropout (p = 0.5)
    (4): Linear (4096 -> 4096)
    (5): ReLU (inplace)
    (6): Linear (4096 -> 1000)
  )
)
  • To get the representation tf.keras offers, use the pytorch-summary package. This contains a lot more details of the model, including:
    • Name and type of all layers in the model.
    • Output shape for each layer.
    • Number of weight parameters of each layer.
    • The total number of trainable and non-trainable parameters of the model.
    • In addition, also offers the following bits not in the Keras summary:
      • Input size (MB)
      • Forward/backward pass size (MB)
      • Params size (MB)
      • Estimated Total Size (MB)
from torchvision import models
from torchsummary import summary

# Example for VGG16
vgg = models.vgg16()
summary(vgg, (3, 224, 224))
  • The output in this case would be something as follows:
----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1         [-1, 64, 224, 224]           1,792
              ReLU-2         [-1, 64, 224, 224]               0
            Conv2d-3         [-1, 64, 224, 224]          36,928
              ReLU-4         [-1, 64, 224, 224]               0
         MaxPool2d-5         [-1, 64, 112, 112]               0
            Conv2d-6        [-1, 128, 112, 112]          73,856
              ReLU-7        [-1, 128, 112, 112]               0
            Conv2d-8        [-1, 128, 112, 112]         147,584
              ReLU-9        [-1, 128, 112, 112]               0
        MaxPool2d-10          [-1, 128, 56, 56]               0
           Conv2d-11          [-1, 256, 56, 56]         295,168
             ReLU-12          [-1, 256, 56, 56]               0
           Conv2d-13          [-1, 256, 56, 56]         590,080
             ReLU-14          [-1, 256, 56, 56]               0
           Conv2d-15          [-1, 256, 56, 56]         590,080
             ReLU-16          [-1, 256, 56, 56]               0
        MaxPool2d-17          [-1, 256, 28, 28]               0
           Conv2d-18          [-1, 512, 28, 28]       1,180,160
             ReLU-19          [-1, 512, 28, 28]               0
           Conv2d-20          [-1, 512, 28, 28]       2,359,808
             ReLU-21          [-1, 512, 28, 28]               0
           Conv2d-22          [-1, 512, 28, 28]       2,359,808
             ReLU-23          [-1, 512, 28, 28]               0
        MaxPool2d-24          [-1, 512, 14, 14]               0
           Conv2d-25          [-1, 512, 14, 14]       2,359,808
             ReLU-26          [-1, 512, 14, 14]               0
           Conv2d-27          [-1, 512, 14, 14]       2,359,808
             ReLU-28          [-1, 512, 14, 14]               0
           Conv2d-29          [-1, 512, 14, 14]       2,359,808
             ReLU-30          [-1, 512, 14, 14]               0
        MaxPool2d-31            [-1, 512, 7, 7]               0
           Linear-32                 [-1, 4096]     102,764,544
             ReLU-33                 [-1, 4096]               0
          Dropout-34                 [-1, 4096]               0
           Linear-35                 [-1, 4096]      16,781,312
             ReLU-36                 [-1, 4096]               0
          Dropout-37                 [-1, 4096]               0
           Linear-38                 [-1, 1000]       4,097,000
================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.57
Forward/backward pass size (MB): 218.59
Params size (MB): 527.79
Estimated Total Size (MB): 746.96
----------------------------------------------------------------

Resources

References

Citation

If you found our work useful, please cite it as:

@article{Chadha2020PyTorchPrimer,
  title   = {PyTorch Primer},
  author  = {Chadha, Aman},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}