Colab Notebook

Introduction

  • NumPy is the core library for scientific computing in Python. It is informally known as the swiss army knife of the data scientist.
  • It provides a high-performance multidimensional array object numpy.ndarray, and tools for operating on these arrays.
  • If you’re already familiar with numerical processing in a different language like MATLAB and R, here are some recommended references:
  • Related primers: Matplotlib and SciPy.

Arrays

  • A NumPy array is a grid of values, all of the same type, and is indexed by a tuple of non-negative integers.
  • The rank of an array is the number of dimensions it contains.
  • The shape of an array is a tuple of integers giving the size of the array along each dimension.
  • The size of an array is the number of elements it contains (which is equivalent to np.prod(<ndarray>.shape), i.e., the product of the array’s dimensions).
  • We can initialize NumPy arrays from (nested) lists and tuples, and access elements using square brackets as array subscripts (similar to lists in Python).
import numpy as np

a = np.array([1, 2, 3])              # Define a rank 1 array using a list
print(type(a))                       # Prints <class 'numpy.ndarray'>
print(a.shape)                       # Prints (3,)
print(a.ndim)                        # Prints 1 (the rank of the array); equivalent to "len(a.shape)"
print(a.size)                        # Prints 3; equivalent to "np.prod(a.shape)"
print(a[0], a[1], a[2])              # Prints (1, 2, 3)
a[0] = 5                             # Change an element of the array
print(a)                             # Prints [5 2 3]

b = np.array([[1, 2, 3]])            # Define a rank 2 array (vector) using a nested list
print(b.shape)                       # Prints (1, 3)
print(b.size)                        # Prints 3

c = np.array([[1, 2, 3], [4, 5, 6]]) # Define a rank 2 array (matrix) using a nested list
print(c.shape)                       # Prints (2, 3)
print(c.size)                        # Prints 6
print(c[0, 0], c[0, 1], c[1, 0])     # Prints (1, 2, 4)

d = np.array((1, 2, 3))              # Define a rank 1 array using a tuple
print(d)                             # Prints [1 2 3]
print(d.shape)                       # Prints (3,)

e = np.array(((1, 2, 3), (4, 5, 6))) # Define a rank 2 array using a nested tuple
print(e)                             # Prints [[1, 2, 3]
                                     #         [4, 5, 6]]
                                     
f = np.array([[1, 2, 3], [4, 5]])    # Define a rank 2 array using
print(f)                             # Prints [list([1, 2, 3]) list([4, 5])]

# NumPy arrays can be initialized using other NumPy arrays or lists
# but note that the resulting matrix is always of type NumPy ndarray
l = [1, 2, 3]                        # Define a python list
g = np.array([l, l, l])              # Matrix initialized with lists
a = np.array([1, 2, 3])              # Define a NumPy array by passing in a list
h = np.array([a, a, a])              # Matrix initialized with NumPy arrays
i = np.array([a, [1, 2, 3], g])      # Matrix initialized with both types

# All the below statements print [[1 2 3]
#                                 [1 2 3]
#                                 [1 2 3]]
print(g)
print(h)
print(i)
  • Note the difference between a Python list and a NumPy array. NumPy arrays are designed for numerical (vector/matrix) operations, while lists are for more general purposes.
import numpy as np

l = [1, 2, 3]           # Define a python list
a = np.array([1, 2, 3]) # Define a numpy array by passing in a list
print(l)                # Prints [1 2 3]
print(a)                # Prints [1 2 3]

print(type(l))          # Prints <class 'list'>
print(type(a))          # Prints <class 'numpy.ndarray'>
  • Note that when defining an array, be sure that all the rows contain the same number of columns/elements. Otherwise, algebraic operations on malformed matrices could lead to unexpected results:
import numpy as np

a = np.array([[1, 2], [3, 4]]) # Define a 2x2 matrix

# Print a scaled version of 'a', more on this in the section on "scaling and translating arrays" below
print(a * 2)                   # Prints [[2 4]
                               #         [6 8]]

# Define a malformed matrix. Note the third row contains 3 elements, while other rows contain 2 elements
b = np.array([[1, 2], [3, 4], [5, 6, 7]])

# Print the malformed matrix
print(b)                       # Prints [list([1, 2]) list([3, 4]) list([5, 6, 7])]

# Supposed to scale the whole matrix but does *not*
print(b * 2)                   # Prints [list([1, 2, 1, 2]) list([3, 4, 3, 4]) list([5, 6, 7, 5, 6, 7])]
  • NumPy also provides many functions to create arrays:
import numpy as np

a = np.array([])                            # Define an empty array
print(a)                                    # Prints array([], dtype=float64)
print(a.shape)                              # Prints (0,)

b = np.zeros((2, 2))                        # Define an array of all zeros
print(b)                                    # Prints [[ 0.  0.]
                                            #         [ 0.  0.]]

c = np.ones((1, 2))                         # Define an array of all ones
print(c)                                    # Prints [[ 1.  1.]]

d = np.full((2, 2), 7)                      # Define a constant array
print(d)                                    # Prints [[ 7.  7.]
                                            #         [ 7.  7.]]

e = np.eye(2)                               # Define a 2x2 identity matrix
print(e)                                    # Prints [[ 1.  0.]
                                            #         [ 0.  1.]]
                                            
f = np.empty((2, 2))                        # Define a float array without initializing entries
print(f)                                    # Prints [[1.13224202e+277 1.94241498e-109]
                                            #         [4.94065646e-323 0.00000000e+000]]

g = np.empty((2, 2), dtype=int)             # Define an int array without initializing entries  
print(g)                                    # Prints [[8751743591039004782 2980593642150976296]   
                                            #         [                 10                   0]]

h = np.random.random((2, 2))                # Define a 2x2 matrix from the uniform distribution [0, 1)
print(h)                                    # Prints a 2x2 matrix of random values 

i = 5 * np.random.random_sample((2, 2)) - 5 # Sample 2x2 matrix from Unif[-5, 0)
                                            # Sample from Unif[a, b), b > a: (b - a) * random_sample() + a
print(i)                                    # Prints a 2x2 matrix of random values 

j = np.random.randn(2, 2)                   # Sample a 2x2 matrix from the standard normal distribution
print(j)                                    # Prints a 2x2 matrix of random values 

k = 2.5 * np.random.randn(2, 2) + 3         # Sample 2x2 matrix from N(mean=3, var=6.25)
                                            # General form: stddev * np.random.randn(...) + mean
print(k)                                    # Prints a 2x2 matrix of random values

  • Note that with np.random.randn(), the length of each dimension of the output array is an individual argument. On the other hand, np.random.random() accepts its shape argument as a single tuple containing all dimensions. More on this in the section on standard normal.

  • To create a new array with the same shape and type as a given array, NumPy offers the following methods:

a = ([1, 2, 3], [4, 5, 6]) # Python list
print(a.shape)

b = np.empty_like(a)
# Uninitialized array
# array([[-1073741821, -1073741821,           3],
#        [          0,           0, -1073741821]])
print(b.shape)             # Prints (2, 3)

c = np.array([[1., 2., 3.], [4., 5., 6.]])
d = np.empty_like(c)
# Uninitialized array
# array([[ -2.00000715e+000,   1.48219694e-323,  -2.00000572e+000], # uninitialized
#        [  4.38791518e-305,  -2.00000715e+000,   4.17269252e-309]])
print(d.shape)             # Prints (2, 3)

# Note the difference between np.ones() and np.ones_like() below.
# np.ones():      Return a new array of given shape and type, filled with ones.
# np.ones_like(): Return a new array with the same shape and type as a given array, filled with ones.
e = np.ones((1, 2, 3))
f = np.ones_like(e)
# array([[[ 1.,  1.,  1.],
#         [ 1.,  1.,  1.]]])
print(e.shape) # Prints (1, 2, 3)
print(f.shape) # Prints (1, 2, 3)

Indexing

  • NumPy arrays can be indexed by integers, a tuple of nonnegative integers, by booleans or by another array.

Integer indexing

  • To “select” a particular row or column in an array, NumPy offers similar functionality as Python lists:
import numpy as np

a = np.array([[1, 2], [3, 4]])

# Select a row
a[0]    # Prints [1 2]
a[1]    # Prints [3 4]

# Select a column
a[:, 0] # Prints [1 3]
a[:, 1] # Prints [2 4]
  • Note that : implies that the entire dimension is selected (as opposed to a particular element or a range of elements within a dimension). Also, if : is the trailing/last element in the index subscript, it can be skipped.
import numpy as np

a = np.ones((1, 2, 3))

# Select the first dimension
a[0].shape       # Prints (2, 3)
a[0,].shape      # Prints (2, 3)
a[0, :].shape    # Prints (2, 3)

# Select the second dimension
a[0, 1].shape    # Prints (3,)
a[0, 1, :].shape # Prints (3,)

Slicing

  • Similar to Python lists, NumPy arrays can be sliced.
  • Since arrays may be multidimensional, you must specify a slice for each dimension of the array:
import numpy as np

# Define the following rank 2 array with shape (3, 4)
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
#  [6 7]]
b = a[:2, 1:3]

# A slice of an array is a "view" into the same data, so modifying it
# will modify the original array
print(a[0, 1])    # Prints 2
print(a[(0, 1)])  # Also prints 2
b[0, 0] = 77      # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1])    # Prints 77
  • You can also mix integer indexing with slice indexing. However, doing so will yield an array of lower rank than the original array.
  • Note that this is quite different from the way that MATLAB handles array slicing:
import numpy as np

# Define the following rank 2 array with shape (3, 4)
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

# Basic slicing
a[0:3]                                # Select rows 0, 1 and 2, all columns
a[0:2, 1]                             # Select rows 0 and 1, column 1
a[:1]                                 # Select row 0, all columns (same as a[0:1, :])
a[1:2, :]                             # Select row 1, all columns

# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array
row_r1 = a[1, :]                      # Rank 1 view of the second row of a
row_r2 = a[1:2, :]                    # Rank 2 view of the second row of a
print(row_r1, row_r1.shape)           # Prints [5 6 7 8] (4,)
print(row_r2, row_r2.shape)           # Prints [[5 6 7 8]] (1, 4)

# We can make the same distinction when accessing columns of an array
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape)           # Prints [ 2  6 10] (3,)
print(col_r2, col_r2.shape)           # Prints [[ 2]
                                      #         [ 6]
                                      #         [10]] (3, 1)

# Mix row and column slicing to print the first 2 rows and alternate 
# columns
arr_row_col = a[:2, ::2]
print(arr_row_col, arr_row_col.shape) # Prints [[1, 3],
                                      #         [5, 7]] (2, 2)

Integer array indexing

  • When you index into NumPy arrays using slicing, the resulting array view will always be a subarray of the original array.
  • In contrast, integer array indexing allows you to construct arbitrary arrays using the data from another array.
  • Here is an example:
import numpy as np

a = np.array([[1, 2], [3, 4], [5, 6]])

# An example of integer array indexing
# The returned array has shape (3,)
rows = [0, 1, 2]
cols = [0, 1, 0]
print(a[rows, cols])                         # Prints [1 4 5]

# or using direct indexing
print(a[[0, 1, 2], [0, 1, 0]])               # Prints [1 4 5]

# The above example of integer array indexing is equivalent to 
# the following:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints [1 4 5]

# Note that this doesn't work and results in
# IndexError: too many indices for array: array is 2-dimensional, 
# but 3 were indexed
print(a[(0, 0), (1, 1), (2, 0)])

# When using integer array indexing, you can reuse the same
# element from the source array
print(a[[0, 0], [1, 1]])                     # Prints [2 2]

# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]]))          # Prints [2 2]
  • You can use np.arange() to select the rows/columns of an array. For more details on np.arange(), refer to the section on arange below.
import numpy as np

a = np.array([[1, 2], [3, 4]])

# Return the entire array
a[np.arange(2), :] # Prints [[1 2]
                   #         [3 4]]

# Return the first row
a[np.arange(1), :] # Prints [[1 2]]
  • Along with np.arange(), you can use an “index array” that contains indices of rows or columns to index into another array. This is a very common use-case in NumPy-based projects.
import numpy as np

a = np.array([[1, 2], [3, 4]])

# Selecting columns using an index array
b = [0, 0]         # Select the first column for both rows (see below)
a[np.arange(1), b] # Prints [1 1] (same as a[0, [0, 0]])
a[np.arange(2), b] # Prints [1 3] (same as a[[0, 1], [0, 0]])

a[:, b]            # Prints [[1 1]
                   #         [3 3]]

# Selecting rows using an index array
b = [0, 0]         # Select the first row for both columns (see below)
a[b, np.arange(1)] # Prints [1 1] (same as a[[0, 0], 0])
a[b, np.arange(2)] # Prints [1 2] (same as a[[0, 0], [0, 1]])        

a[b, :]            # Prints [[1 2]
                   #         [1 2]]
  • One useful trick with np.arange() and index array is selecting or mutating one element from each row of a matrix:
import numpy as np

# Define a new array from which we will select elements
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])

print(a)                   # Prints [[ 1  2  3]
                           #         [ 4  5  6]
                           #         [ 7  8  9]
                           #         [10 11 12]]

# Define an array of indices
b = np.array([0, 2, 0, 1])

# Select one element from each row of a using the indices in b
print(a[np.arange(4), b])  # Prints [ 1 6 7 11]

# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10

print(a)                   # Prints [[11  2  3]
                           #         [ 4  5 16]
                           #         [17  8  9]
                           #         [10 21 12]]

Boolean array indexing

  • Boolean array indexing lets you pick out arbitrary elements of an array.
  • This type of indexing is frequently used to select the elements of an array that satisfy some condition.
  • Here is an example:
import numpy as np

a = np.array([[1, 2], [3, 4]])

print(a[True])     # Same as print(a), interpreted as a "True" mask 
                   # on each of a's elements
                   # Prints [[[1 2]
                   #          [3 4]]]

bool_idx = (a > 2) # Find the elements of a that are bigger than 2;
                   # this returns a NumPy array of Booleans of the same
                   # shape as a, where each slot of bool_idx tells
                   # whether that element of a is > 2

print(bool_idx)    # Prints [[False False]
                   #         [ True  True]]

# We use boolean array indexing to construct a rank 1 array
# consisting of the elements of a corresponding to the True values
# of bool_idx
print(a[bool_idx]) # Prints [3 4]

# We can do all of the above in a single concise statement:
print(a[a > 2])    # Prints [3 4]
  • As an extension of the above concept, to select elements on an array based on the elements of another array:
import numpy as np

a = np.array([1, 2, 3, 4, 5, 6])
b = np.array(['f','o','o','b','a','r'])

# Note that & is the bitwise AND operator, and && is not supported in NumPy,
# so np.logical_and() is used in the below example
print(b[np.logical_and((a > 1), (a < 5))]) # Prints ['o' 'o' 'b']

# Another way to accomplish this is using np.all(), 
# which is explained in the section on "all" below.
print(b[np.all([a > 1, a < 5], axis=0)])   # Prints ['o' 'o' 'b']
  • For brevity, we have left out a lot of details about NumPy array indexing; if you want to know more you should read the NumPy documentation.

Datatypes

  • Every NumPy array is a grid of elements of the same type.
  • NumPy provides a large set of numeric datatypes that you can use to construct arrays.
  • NumPy tries to guess a datatype when you create an array, but functions that construct arrays usually also include an optional argument to explicitly specify the datatype.
  • As an example:
import numpy as np

x = np.array([1, 2])                 # Let NumPy choose the datatype
print(x.dtype)                       # Prints int64

x = np.array([1.0, 2.0])             # Let NumPy choose the datatype
print(x.dtype)                       # Prints float64

x = np.array([1, 2], dtype=np.int64) # Force a particular datatype
print(x.dtype)                       # Prints int64
  • Note that with NumPy, the default float datatype is float64 (double precision), while that with PyTorch is float32 (single precision). However, the default int datatype for both NumPy and PyTorch is int64.
  • You can read all about datatypes in the NumPy documentation.

Changing datatypes

  • The astype() method of np.ndarray can change the datatype.
import numpy as np

a = np.array([1, 2, 3])
print(a)             # Prints [1 2 3]
print(a.dtype)       # Prints int64

a_float = a.astype(np.float32)
print(a_float)       # Prints [1. 2. 3.]
print(a_float.dtype) # Prints float32

# 'a' remains unchanged.
print(a)              # Prints [1 2 3]
print(a.dtype)        # Prints int64

a_str = a.astype('str')
print(a_str)          # Prints ['1' '2' '3']
print(a_str.dtype)    # Prints <U21

Array math

  • NumPy provides many functions for manipulating arrays; you can find an exhaustive list in the NumPy documentation. Some common ones are listed below.

Element-wise operations

  • Algebraic operations such as +, -, *, / etc. are available both as operator overloads and as functions in the NumPy module. These operators carry out element-wise operations on NumPy arrays:
import numpy as np

x = np.array([[1, 2], [3, 4]], dtype=np.float64)
y = np.array([[5, 6], [7, 8]], dtype=np.float64)

# Elementwise sum; both produce the array
# [[ 6.0  8.0]
#  [10.0 12.0]]
print(x + y)
print(np.add(x, y))

# Elementwise difference; both produce the array
# [[-4.0 -4.0]
#  [-4.0 -4.0]]
print(x - y)
print(np.subtract(x, y))

# Elementwise product; both produce the array
# [[ 5.0 12.0]
#  [21.0 32.0]]
print(x * y)
print(np.multiply(x, y))

# Elementwise division; both produce the array
# [[ 0.2         0.33333333]
#  [ 0.42857143  0.5       ]]
print(x / y)
print(np.divide(x, y))

# Elementwise square root; produces the array
# [[ 1.          1.41421356]
#  [ 1.73205081  2.        ]]
print(np.sqrt(x))

NumPy arrays vs. Python lists

  • A common mistake is to mix up the concepts of NumPy arrays and Python lists.
  • Note that the + operator in the context of NumPy arrays performs an element-wise addition, while the same operation on Python lists results in a list extension.
import numpy as np

l = [1, 2, 3]           # Define a python list
a = np.array([1, 2, 3]) # Define a numpy array by passing in a list
print(a + a)            # Prints [2 4 6]
print(l + l)            # Prints [1 2 3 1 2 3]
  • With NumPy arrays, we can scale the vector with * by performing element-wise multiplication, while the same operation on Python lists results in a list concatenation (and in MATLAB, results in matrix multiplication).
    • We instead use the dot function to compute inner products of vectors, to multiply a vector by a matrix, and to multiply matrices. We discuss this in detail in the section on dot product below.
import numpy as np

l = [1, 2, 3]           # Define a python list
a = np.array([1, 2, 3]) # Define a numpy array by passing in a list
print(a * 3)            # Prints [3 6 9]
print(l * 3)            # Prints [1 2 3 1 2 3 1 2 3]
  • Make note of this while coding since a function can utilize both Python lists and NumPy arrays. Knowing this can save many headaches!

Scaling and translating arrays

  • Using regular algebraic operators like + and - that we saw in the prior section on element-wise operations, we can scale and translate/shift NumPy arrays.
  • Operations can be performed between:
    • Two NumPy arrays or,
    • NumPy arrays and scalars.
import numpy as np

a = np.array([[1, 2], [3, 4]]) # Define a 2x2 matrix

# Scale by 2 units and translate by 1 unit
result = a * 2 + 1             # Multiply each element in the matrix by 2 and add 1
print(result)                  # Prints [[3 5]
                               #         [7 9]]

Norm

  • NumPy offers a set of algebraic functions in the class linalg, which includes the norm function:
import numpy as np

a = np.array([1, 2, 3, 4])     # Define an array
norm1 = np.linalg.norm(a)

a = np.array([[1, 2], [3, 4]]) # Define a 2x2 matrix
norm2 = np.linalg.norm(a) 

# Both print 5.477225575051661
print(norm1)
print(norm2)
  • By default, np.linalg.norm() calculates the Frobenius norm for matrices and the 2-norm for vectors, unless the ord argument is overridden.
    • Recall from linear algebra that the norm (or magnitude) of an n-dimensional vector \(v\) is the square root of the sum of its elements squared:
    \[norm(\vec{v})=||\vec{v}||_{2}=\sqrt{\sum_{i=1}^{n} v_{i}^{2}}\]
    • Also, the Frobenius norm is the generalization of the vector norm for matrices, and is defined for a matrix \(A\) as:
    \[\|\mathrm{A}\|_{F} = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n}\left|a_{i j}\right|^{2}}\]
  • The following code snippet compares a manual implementation of the norm vs. the np.linalg.norm() function. Both yield the same result.
import numpy as np

a = np.array([[1, 2], [3, 4]]) # Define a 2x2 matrix

norm = np.sqrt(np.sum(np.square(a)))

# Both should yield the same result and print:
# 5.477225575051661 ==  5.477225575051661
print(norm, '== ', np.linalg.norm(a))

a = np.array([1, 2, 3, 4])     # Define an array

norm = np.sqrt(np.sum(np.square(a)))

# Both should yield the same result and print:
# 5.477225575051661 ==  5.477225575051661
print(norm, '== ', np.linalg.norm(a))
  • Note that if the axis argument to np.linalg.norm() is not explicitly specified, the function defaults to treating the matrix as a “flat” array of numbers implying that it takes every element of the matrix into account. However, it is possible to get the a row-wise or column-wise norm using the axis parameter:
    • axis=0 operates across all rows, i.e., gets the norm of each column.
    • axis=1 operates across all columns, i.e., gets the norm of each row.
import numpy as np

a = np.array([[1, 1], [2, 2], [3, 3]]) # Define a 3x2 matrix

normByCols = np.linalg.norm(a, axis=0) # Get the norm for each column; returns 2 elements
normByRows = np.linalg.norm(a, axis=1) # get the norm for each row; returns 3 elements

print(normByCols)                      # [3.74165739 3.74165739]
print(normByRows)                      # [1.41421356 2.82842712 4.24264069]

Dot product

  • Dot product is available both as a function in the NumPy module np.dot() and as an instance method of array objects <ndarray>.dot():
import numpy as np

x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])

v = np.array([9, 10])
w = np.array([11, 12])

# Dot/scalar/inner product of vectors; both produce a scalar: 219
print(v.dot(w))
print(np.dot(v, w))

# Matrix/vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))

# Matrix/matrix product; both produce the rank 2 array
# [[19 22]
#  [43 50]]
print(x.dot(y))
print(np.dot(x, y))
  • Some alternative ways to obtain the dot product:
import numpy as np

print(np.sum(v * w)) # Using the definition of dot product

print(v @ w)         # numpy>=1.10 overloads the new Pythonic operator "@" for dot product

# Inefficient, unrolled, non-vectorized implementation
dotProduct = 0
for a, b in zip(v, w):
    dotProduct += a * b 
    
print(dotProduct)
  • While a @ b and np.sum() accept only NumPy arrays, np.dot() accepts both NumPy arrays and Python lists:
import numpy as np

n1 = np.dot(np.array([1, 2]), np.array([3, 4])) # Dot product on NumPy arrays
n2 = np.dot([1, 2], [3, 4])                     # Dot product on python lists

# Both print 11
print(n1)
print(n2)

  • Note that while np.dot() accepts 2D arrays (and carries out matrix multiplication), using np.matmul() or a @ b for NumPy arrays is preferred. The section on Matrix Product talks about how np.matmul() differs from np.dot().

  • The following rules dictate the behavior of np.dot() depending on the arguments:

    • If both a and b are 1D arrays, it is the inner product of a and b.
    • If both a and b are 2D arrays, it is matrix multiplication, but using np.matmul(a, b) or a @ b is preferred.
    • If either argument is 0D (scalar), it is scalar multiplication and using np.multiply(a, b) or a * b is preferred.
    • If a is an N-dimensional array and b is a 1-dimensional array, it is a sum product over the last axis of a and b.

    • If a is an N-dimensional array and b is an M-dimensional array (where \(M \geq 2\)), it is a sum product over the last axis of a and the second-to-last axis of b:

        dot(a, b)[i, j, k, m] = sum(a[i, j, :] * b[k, :, m])
      • As an example,
        import numpy as np

  a = np.ones([9, 5, 7, 4])
  c = np.ones([9, 5, 4, 3])
  print(np.dot(a, c).shape) # Prints (9, 5, 7, 9, 5, 3)

Broadcasting

  • Broadcasting is a powerful mechanism that allows NumPy to work with arrays of different shapes when performing arithmetic operations. Frequently, we have a smaller array and a larger array, and we want to use the smaller array multiple times to perform some operation on the larger array.
  • Broadcasting typically makes your code more concise and faster, so you should strive to use it where possible.
  • The simplest broadcasting example occurs when an array and a scalar value are combined in an operation:
import numpy as np

a = np.array([1, 2, 3])
b = 2
print(a * b) # Prints [2 4 6]

# Note that the result is equivalent to the next example where b is an array!
a = np.array([1, 2, 3])
b = np.array([2, 2, 2])
print(a * b) # Prints [2 4 6]
  • Consider another example where we’d like to add a constant vector to each row of a matrix. We could do it like this:
import numpy as np

# We will add the vector v to each row of the matrix x, 
# storing the result in the matrix y
x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Define an empty matrix with the same shape as x

# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
    y[i, :] = x[i, :] + v

# Now y is the following
# [[ 2  2  4]
#  [ 5  5  7]
#  [ 8  8 10]
#  [11 11 13]]
print(y)
  • This works; however when the matrix x is very large, computing an explicit loop in Python could be slow.
  • Note that adding the vector v to each row of the matrix x is equivalent to forming a matrix vv by stacking multiple copies of v vertically, then performing element-wise summation of x and vv. We could implement this approach like this:
import numpy as np

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
v = np.array([1, 0, 1])
vv = np.tile(v, (4, 1)) # Stack 4 copies of v on top of each other
print(vv)               # Prints [[1 0 1]
                        #         [1 0 1]
                        #         [1 0 1]
                        #         [1 0 1]]
y = x + vv              # Add x and vv element-wise
print(y)                # Prints [[ 2  2  4
                        #         [ 5  5  7]
                        #         [ 8  8 10]
                        #         [11 11 13]]
  • NumPy broadcasting allows us to perform this computation without actually creating multiple copies of v. Consider this version, using broadcasting:
import numpy as np

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y)  # Prints [[ 2  2  4]
          #         [ 5  5  7]
          #         [ 8  8 10]
          #         [11 11 13]]
  • The line y = x + v works even though x has shape (4, 3) and v has shape (3,) due to broadcasting; this line works as if v actually had shape (4, 3), where each row was a copy of v, and the sum was performed element-wise.

Rules

  • Broadcasting two arrays together follows these rules:
    • If the arrays do not have the same rank, prepend the shape of the lower rank array with ones until both shapes have the same length.
      • This implies that the arrays do not need to have the same number of dimensions.
    • If the arrays have the same rank, NumPy compares their shapes element-wise. It starts with the trailing dimensions and works its way forward, checking if the arrays are compatible in every dimension, as follows:
      • The two arrays are said to be compatible in a dimension if:
        • They have the same size in the dimension or,
        • One of the arrays has size 1 in that dimension.
      • The arrays can only be broadcast together if they are compatible in all dimensions.
      • When either of the dimensions belonging to both arrays being compared is 1, the other is used. In other words, dimensions with size 1 are stretched or “copied” to match the other. This is the primary broadcasting step.
      • After broadcasting, each array behaves as if it its shape is now equal to the element-wise maximum of shapes of the two input arrays.
  • Functions that support broadcasting are known as universal functions. You can find an exhaustive list of universal functions in the NumPy documentation.

Examples

  • Examples from NumPy’s documentation on Broadcasting:

    1. Either array has axes with length 1: In the following example, array \(B\) has an axis with length 1.
      • To tackle an axis with length 1 during broadcasting, we simply expand that dimension to match the other array’s.
       A      (3d array):  15 x 3 x 5
 B      (3d array):  15 x 1 x 5
 Result (3d array):  15 x 3 x 5
    2. Both arrays have axes with length 1: In the following example, arrays \(A\) and \(B\) both have axes with length 1.
      • Extrapolating the case above, to tackle an axis with length 1 in either array during broadcasting, we simply expand that dimension to match the other array’s.
       A      (4d array):  8 x 1 x 6 x 1
 B      (3d array):      7 x 1 x 5
 Result (4d array):  8 x 7 x 6 x 5
    3. Rank mismatch: In the following example, arrays \(A\) and \(B\) do not have the same rank.
      • Recall that to tackle rank mismatch during broadcasting, we prepend the shape of the lower rank array with ones until both shapes have the same length.
       A      (2d array):  5 x 4
 B      (1d array):      4
 Result (2d array):  5 x 4

       A      (3d array):  15 x 3 x 5
 B      (2d array):       3 x 5
 Result (3d array):  15 x 3 x 5

       A      (3d array): 256 x 256 x 3
 B      (1d array):             3
 Result (3d array): 256 x 256 x 3
    4. Rank mismatch and axes with length 1: In the following example, arrays \(A\) and \(B\) do not have the same rank and \(B\) has an axis of length 1.
      • Tackling rank mismatch was discussed in example 3. Also, handling an axis with length 1 was discussed in example 1.
       A      (2d array):  5 x 4
 B      (1d array):      1
 Result (2d array):  5 x 4

       A      (3d array):  15 x 3 x 5
 B      (2d array):       3 x 1
 Result (3d array):  15 x 3 x 5

  • Some examples that do not broadcast:

    1. Dimension mismatch: In the following example, arrays \(A\) and \(B\) are not compatible in each dimension and thus, cannot be broadcasted.
      • Recall that the two arrays need to be compatible in each dimension (starting from the trailing dimension) for broadcasting to be defined.
       A      (1d array):  3
 B      (1d array):  4         # Trailing dimensions do not match

       A      (2d array):      2 x 1
 B      (3d array):  8 x 4 x 3 # Second from last dimensions mismatched

  • Broadcasting examples in code:

import numpy as np

# Compute outer product of vectors
v = np.array([1, 2, 3]) # v has shape (3,)
w = np.array([4, 5])    # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4  5]
#  [ 8 10]
#  [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Note that np.reshape() is described in detail in the section on "reshape" below.

# Add a vector to each row of a matrix
x = np.array([[1, 2, 3], [4, 5, 6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
#  [5 7 9]]
print(x + v)

# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,)
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5  6  7]
#  [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))

# Multiply a matrix by a constant:
# x has shape (2, 3). NumPy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2  4  6]
#  [ 8 10 12]]
print(x * 2)

Data centering

  • In some scenarios, centering the elements of a dataset is an important preprocessing step. Centering a dataset involves subtracting the mean from the data. The resultant data is called zero-centered, since the mean of the resultant dataset is 0.

Column-centering

  • Column-centering a matrix involves subtracting the column mean from each element within a particular column. Note that the sum by columns of a centered matrix is always 0.
import numpy as np

a = np.array([[1, 1], [2, 2], [3, 3]]) # Define a 3x2 matrix. 

centered = a - np.mean(a, axis=0)      # Remove the mean for each column

# Column-centered matrix
print(centered)                        # Prints [[-1. -1.]
                                       #         [ 0.  0.]
                                       #         [ 1.  1.]]

# New mean-by-column should be 0
print(centered.mean(axis=0))           # Prints [0. 0.]

Row-centering

  • For row centering, transpose the matrix, center by columns, and then transpose back the result.
import numpy as np

a = np.array([[1, 3], [2, 4], [3, 5]]) # Define a 3x2 matrix. 

centered = a.T - np.mean(a, axis=1)    # Remove the mean for each row
centered = centered.T                  # Transpose back the result

# Row-centered matrix
print(centered)                        # Prints [[-1.  1.]
                                       #         [-1.  1.]
                                       #         [-1.  1.]]

# New mean-by-rows should be 0
print(centered.mean(axis=1))           # Prints [0. 0. 0.]

Selected methods

  • NumPy provides a host of useful functions for performing computations on arrays. Below, we’ve touched upon some of the most useful ones that you’ll encounter regularly in projects.
  • You can find an exhaustive list of mathematical functions in the NumPy documentation.
  • As discussed in the section on norm, most of these functions accept an axis parameter which when specified, performs the operation on a per-column (axis=0) or per-row basis (axis=1) rather than on the entire array.

Asarray

  • np.asarray() converts the input to an array.
# Convert a list into an array
a = [1, 2]
print(np.asarray(a)) # array([1, 2])

# Existing NumPy arrays are not copied
a = np.array([1, 2])
np.asarray(a) is a # Prints True

# If dtype is set, array is copied only if dtype does not match:
a = np.array([1, 2], dtype=np.float32)
np.asarray(a, dtype=np.float32) is a # Prints True
np.asarray(a, dtype=np.float64) is a # Prints False
  • Note that the main difference between np.asarray() and np.array() is that np.array() will make a copy of the object by default, while np.asarray() will not unless the input and target are not compatible.

Initialization

Random seed

  • Provide a seed to the generator. Used to ensure reproducibility of random numbers.
import numpy as np

np.random.seed(0)        # Here, 0 is the seed.

a = np.random.rand()
print(a)                 # Print 0.5488135039273248

np.random.seed(0)        # Set seed again for next random number to match the prior one.

b = np.random.rand()
print(b)                 # Print 0.5488135039273248

c = np.random.rand(3, 2) # Initialize a 3x2 matrix of random values with seed 0
print(c)                 # Prints a 3x2 matrix of random values

Standard normal

  • Return samples from the standard normal (also called the standard Gaussian) distribution.
  • Note that np.random.randn() is a convenience function for users porting code from MATLAB, and wraps np.random.standard_normal(). As such, np.random.randn() takes dimensions as individual integers.
    • On the other hand, np.random.standard_normal() takes a shape argument as a tuple to specify the size of the output, which is consistent with other NumPy functions like np.zeros() and np.ones().
import numpy as np

a = np.random.randn(2, 2)             # Sample a 2x2 matrix from the standard normal distribution
print(a)                              # Print a 2x2 matrix of random values 

b = np.random.standard_normal((2, 2)) # Sample a 2x2 matrix from the standard normal distribution
print(b)                              # Print a 2x2 matrix of random values
  • To sample the normal distribution \(a \sim \mathcal{N}(\mu, \sigma^2)\), multiply the output of np.random.randn() by \(\sigma\) and add \(\mu\), i.e., stddev * np.random.randn(...) + mean}:
import numpy as np

a = 2.5 * np.random.randn(2, 2) + 3 # Sample a 2x2 matrix from N(mean=3, var=6.25)
                                    # General form: stddev * np.random.randn(...) + mean
print(a)                            # Print a 2x2 matrix of random values

Uniform

  • Samples random floats from a continuous uniform distribution – the half-open interval \([0.0, 1.0)\).
  • Note that np.random.rand() is a convenience function for users porting code from MATLAB, and wraps np.random.random(). As such, np.random.rand() takes dimensions as individual ints.
    • On the other hand, np.random.random() takes a shape argument as a tuple to specify the size of the output, which is consistent with other NumPy functions like np.zeros() and np.ones().
import numpy as np

a = np.random.rand(2, 2)     # Define a 2x2 matrix from the uniform distribution [0, 1)
print(a)                     # Print a 2x2 matrix of random values 

b = np.random.random((2, 2)) # Define a 2x2 matrix from the uniform distribution [0, 1)
print(b)                     # Print a 2x2 matrix of random values
  • To sample the uniform distribution \(a \sim Unif[x, y)\), given \(y > x\), Note that np.random.uniform() offers this functionality (drawing samples from a uniform distribution within an arbitrary range) much more directly by accepting three arguments: low=0.0, high=1.0, size=None. The following code snippet thus yields the same output as the one above.
import numpy as np

a = np.random.uniform(-5, 0, size=(2,2)) # Sample 2x2 matrix from Unif[-5, 0)

print(a)                                 # Print a 2x2 matrix of random values
  • Note that np.random.random() also offers this functionality (drawing samples from a uniform distribution within an arbitrary range) by multiplying its output by \((y-x)\) and adding \(x\), i.e., (y - x) * np.random.random(...) + x
import numpy as np

a = 5 * np.random.random((2, 2)) - 5 # Sample 2x2 matrix from Unif[-5, 0)
                                     # Sample from Unif[x, y), y > x: (y - x) * np.random.random() + x
print(a)                             # Print 2x2 matrix of random values
  • Without explicit arguments, the functions rand(), random(), uniform() and random_sample() are equivalent, producing a random float in the range \([0.0, 1.0)\).
import numpy as np

np.random.seed(0)

a = np.random.rand()
print(a)                      # Print 0.5488135039273248

b = np.random.random()
print(b)                      # Print 0.7151893663724195

c = np.random.uniform()
print(c)                      # Print 0.6027633760716439

d = np.random.random_sample() # numpy.random.random() is an alias for numpy.random.random_sample()
print(d)                      # Print 0.5448831829968969

ndarray.item(): Convert Single Value Tensor to Scalar

  • Returns the value of an ndarray as a Python int/float. This only works for arrays with one element. For other cases, see [tolist()](#ndarraytolist-convert-multi-value-tensor-to-scalar).
import numpy as np

a = np.asarray([1.0])
a.item()   # Prints 1.0

a.tolist() # Prints [1.0]

ndarray.tolist(): Convert Multi Value Tensor to Scalar

  • Returns the ndarray as a (nested) list. For scalars, a standard Python number is returned, just like with [item()](#ndarrayitem-convert-single-value-tensor-to-scalar).
import numpy as np

a = np.random.random((2, 2))
a.tolist()      # Prints [[0.012766935862600803, 0.5415473580360413],
                #         [-0.08909505605697632, 0.7729271650314331]]
a[0,0].tolist() # Prints 0.012766935862600803

Random choice

  • Generates a random sample from a given 1D array. The main arguments to np.random.choice() are a and size.
    • a can be an ndarray, in which case a random sample is returned from its elements. If it’s an int, the random sample is generated as if a were np.arange(a).
    • size is an optional argument that can hold an int or a tuple of ints. If it is not overriden, a single value is returned by default.
import numpy as np

# Generate a uniform random sample from np.arange(5) of size 3
# This is equivalent to np.random.randint(0, 5, 3) or np.random.randint(0, 5, size=3)
print(np.random.choice(5, 3))                          # Prints [0 3 4]

# Generate a non-uniform random sample from np.arange(5) of size 3
print(np.random.choice(5, 3, p=[0.1, 0, 0.3, 0.6, 0])) # Prints [3 3 0]

# Generate a uniform random sample from np.arange(5) of size 3 without replacement
print(np.random.choice(5, 3, replace=False))           # Prints [4 1 3]

Nonzero

  • Return the indices of the elements that are non-zero using a tuple of arrays, one for each dimension of the input array, containing the indices of the non-zero elements in that dimension. The values in the input array are always tested and returned in row-major, C-style order.
import numpy as np

a = np.array([[3, 0, 0], [0, 4, 0], [5, 6, 0]])
print(np.nonzero(a))               # Prints (array([0, 1, 2, 2]), array([0, 1, 0, 1]))
print(a[np.nonzero(a)])            # Prints [3 4 5 6]
print(np.transpose(np.nonzero(a))) # Prints [[0, 0],
                                   #         [1, 1],
                                   #         [2, 0],
                                   #         [2, 1]])
  • A common use for nonzero is to find the indices of an array, where a condition is true. Given an array a, the condition a > 3 is a boolean array and since False is interpreted as 0, np.nonzero(a > 3) yields the indices of the a where the condition is true.
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
a > 3             # Prints array([[False, False, False],
                  #               [ True,  True,  True],
                  #               [ True,  True,  True]])
np.nonzero(a > 3) # Prints (array([1, 1, 1, 2, 2, 2]), array([0, 1, 2, 0, 1, 2]))
  • Using this result to index the array is equivalent to using the mask directly:
a[np.nonzero(a > 3)]
array([4, 5, 6, 7, 8, 9])
a[a > 3]  # prefer this spelling
array([4, 5, 6, 7, 8, 9])
  • nonzero can also be called as a method of the array.
(a > 3).nonzero()
(array([1, 1, 1, 2, 2, 2]), array([0, 1, 2, 0, 1, 2]))

Arange

  • Return evenly spaced values within the half-open interval \([start, stop)\) (in other words, the interval including start but excluding stop).
  • For integer arguments the function is equivalent to the Python built-in range function, but returns an ndarray rather than a list.
import numpy as np

print(np.arange(8))             # Prints [0 1 2 3 4 5 6 7]
print(np.arange(3, 8))          # Prints [3 4 5 6 7]
print(np.arange(3, 8, 2))       # Prints [3 5 7]

# arange() works with floats too (but read the disclaimer below)
print(np.arange(0.1, 0.5, 0.1)) # Prints [0.1 0.2 0.3 0.4]
  • When using a non-integer step, such as \(0.1\), the results can often be inconsistent. It is better to use np.linspace() for those cases as below.

Linspace

  • Return evenly spaced numbers over a specified interval.
  • Returns 50 evenly spaced samples (which can be overriden by num), calculated over the interval \([start, stop]\).
import numpy as np

print(np.linspace(2.0, 3.0, num=5))                 # Prints [2.   2.25 2.5  2.75 3.  ]
print(np.linspace(2.0, 3.0, num=5, endpoint=False)) # Prints [2.   2.2  2.4  2.6  2.8]

Reshape

  • Gives a new shape to an array without changing its data.
  • Note that np.reshape() returns a view of the array when the elements are contiguous in memory (just like np.ravel()). So modifying the result of np.reshape() would also modify the original array. However, np.reshape() returns a copy if, for e.g., the input array were made from slicing another array using a non-unit step size (e.g. a = x[::2]).
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

print(np.reshape(a, (3, 2)) # Prints [[1 2]
                            #         [3 4]
                            #         [5 6]]

print(np.reshape(a, 6))     # Prints [1 2 3 4 5 6]

-1 in Reshape

  • NumPy allows us to assign one (and only one) value of the shape argument to a function as -1. NumPy figures out the unknown dimension by looking at the length of the array and the remaining dimensions, while making sure it satisfies the criterion that the new shape should be compatible with the original shape.
import numpy as np

a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(a.shape)   # Prints (3, 4)

# Reshaping with *just* (-1) leads to array flattening. 
# Yields new shape as (12,), a rank 1 array which is compatible with original shape (3, 4)
print(a.reshape(-1))    # Prints [ 1  2  3  4  5  6  7  8  9 10 11 12]
# Note that np.reshape(-1) returns the same result as np.flatten()
# with the exception that np.flatten() returns a copy while reshape() returns a view of the original array.
# For more on np.flatten(), refer the section on "flatten" below.

# Transform the input array to a row vector by reshaping with (1, -1), i.e., 1 row and 3*4 number of columns.
# Yields new shape as (1, 12), a rank 2 array which is compatible with original shape (3, 4)
print(a.reshape(1, -1)) # Prints [[ 1  2  3  4  5  6  7  8  9 10 11 12]]

# Transform the input array to a column vector by reshaping with (-1, 1), i.e., 3*4 number of rows and 1 column.
# Yields new shape as (12, 1), a rank 2 array which is compatible with original shape (3, 4)
print(a.reshape(-1, 1)) # Prints [[ 1]
                        #         [ 2]
                        #         [ 3]
                        #         [ 4]
                        #         [ 5]
                        #         [ 6]
                        #         [ 7]
                        #         [ 8]
                        #         [ 9]
                        #         [10]
                        #         [11]
                        #         [12]]

Transpose

  • To transpose a 2D array (matrix), i.e., swap rows and columns, simply use the T attribute of an array object. Note that np.transpose() and <ndarray>.transpose() also yield the same result.
import numpy as np

a = np.array([[1, 2], [3, 4]])
print(a)               # Prints [[1 2]
                       #         [3 4]]
print(a.T)             # Prints [[1 3]
                       #         [2 4]]
print(np.transpose(a)) # Prints [[1 3]
                       #         [2 4]]
  • Note that taking the transpose of a rank 1 (1D) array does nothing:
import numpy as np

a = np.array([1, 2, 3])
print(a)               # Prints [1 2 3]
print(a.T)             # Prints [1 2 3]
  • Instead, to “transpose” a rank 1 array, use [np.newaxis](#new-axis):
import numpy as np

a = np.array([1, 2, 3])

# Make "a" a row vector by inserting an axis along first dimension
print(a[np.newaxis, :]) # Prints [[1 2 3]]
                        
# Make "a" a column vector by inserting an axis along second dimension
print(a[:, np.newaxis]) # Prints [[1]
                        #         [2]
                        #         [3]]

import numpy as np

a = np.array([1, 2, 3])

# Here, "None" serves as a shortcut for np.newaxis and yields the same row vector 
print(a[None, :])       # Prints [[1 2 3]]
                        
# Here, "None" serves as a shortcut for np.newaxis and yields the same column vector
print(a[:, None])       # Prints [[1]
                        #         [2]
                        #         [3]]
  • With np.transpose(), you can not only transpose a matrix but also rearrange/permute the axes of a multidimensional array in any order. This functionality is similar to what PyTorch offers using torch.permute() (but note that torch.transpose() only swaps two dimensions).
import numpy as np

a = np.ones((1, 2, 3))
print(a.shape)                          # Prints (1, 2, 3)
print(np.transpose(a, (1, 0, 2)).shape) # Prints (2, 1, 3)

Internals

  • The way NumPy internally accomplishes a transpose is by swapping the shape and stride information for each axis. This section details what happens under-the-hood when NumPy performs a transpose.

  • Let’s start with a \(2 \times 2 \times 4\) matrix and see how it’s transpose looks:

      import numpy as np    
    
  a = np.arange(24).reshape((2, 3, 4))

  print(a) # Prints [[[ 0  1  2  3]
           #          [ 4  5  6  7]
           #          [ 8  9 10 11]]
           #        
           #         [[12 13 14 15]
           #          [16 17 18 19]
           #          [20 21 22 23]]]

  b = a.transpose((1, 0, 2))
  print(b) # Prints [[[ 0  1  2  3]
           #          [12 13 14 15]]
           #        
           #         [[ 4  5  6  7]
           #          [16 17 18 19]]
           #        
           #         [[ 8  9 10 11]
           #          [20 21 22 23]]]
    • Now, let’s check the strides for the array before the transpose:
      import numpy as np    

  a.shape   # Prints (2, 3, 4)
  a.strides # Prints (96, 32, 8)
    • Now, let’s check the strides for the array after the transpose:
      import numpy as np    

  b.shape   # Prints (3, 2, 4)
  b.strides # Prints (32, 96, 8)
  • Note that the transpose operation swapped the lengths and strides for axis 0 and axis 1. No data needs to be copied for this to happen; NumPy can simply change how it looks at the underlying memory to construct the new array. Here’s how:
    • The stride value represents the number of bytes that must be traversed in memory in order to reach the next value of an axis of an array.
    • Now, our 3D array looks this (with labelled axes):

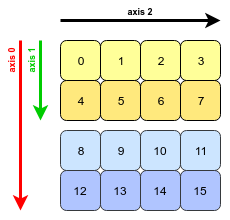
    • This array is stored in a contiguous block of memory (i.e., to access the next value in the array, we just move to the next memory address); essentially it is one-dimensional. To interpret it as a 3D object, NumPy must jump over a certain constant number of bytes in order to move along one of the three axes:

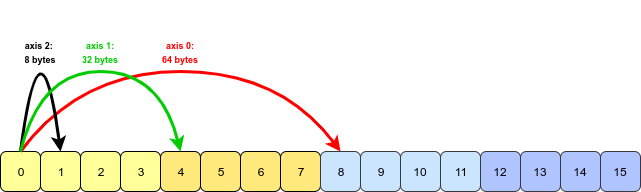
    • Since each integer takes up 8 bytes of memory (we’re using the int64 dtype), the stride value for each dimension is 8 times the number of values that we need to jump. For instance, to move along axis 1, four values (32 bytes) are jumped, and to move along axis 0, eight values (64 bytes) need to be jumped.
    • When we write a.transpose(1, 0, 2), we are swapping axes 0 and 1. The transposed array looks like this:

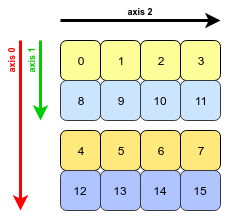
    • All that NumPy needs to do is to swap the stride information for axis 0 and axis 1 (axis 2 is unchanged). Now we must jump further to move along axis 1 than axis 0:

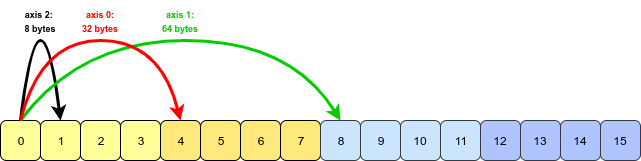
    • This basic concept works for any permutation of an array’s axes. The actual code that handles the transpose is written in C and can be found here.

Reverse

  • Reverse (or flip) the contents of an array along an axis.
  • If axis is not specified, it is assumed None, which flips over all of the axes of the input array.
  • If axis is a tuple of ints, flipping is performed on all of the axes specified in the tuple.
import numpy as np

a = np.arange(8).reshape((2, 2, 2))

print(a)                  # Prints [[[0 1]
                          #          [2 3]]
                          #     
                          #         [[4 5]
                          #          [6 7]]]

print(np.flip(a, 0))      # Prints [[[4 5]
                          #          [6 7]]
                          #
                          #         [[0 1]
                          #          [2 3]]]

print(np.flip(a, 1))      # Prints [[[2 3]
                          #          [0 1]]
                          #         
                          #         [[6 7]
                          #          [4 5]]]

print(np.flip(a))         # Prints [[[7 6]
                          #          [5 4]]
                          #
                          #         [[3 2]
                          #          [1 0]]]

print(np.flip(a, (0, 2))) # Prints [[[5 4]
                          #          [7 6]]
                          #
                          #         [[1 0]
                          #          [3 2]]]

Flatten

  • Return a copy of the array collapsed into one dimension.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
print(a.flatten()) # Prints [1 2 3 4 5 6]

Squeeze

  • Remove single-dimensional axes from an input array.
  • The “squeeze” nomenclature has been borrowed from MATLAB which removes axes of size one (singletons).
import numpy as np

a = np.array([[[0], [1], [2]]])

print(a.shape)             # Prints (1, 3, 1)
print(np.squeeze(a))       # Prints [0 1 2]
print(np.squeeze(a).shape) # Prints (3,)
print(a) # Prints [[[0]
         #          [1]
         #          [2]]]
  • Note that unlike PyTorch, NumPy does not have offer an unsqueeze function, but similar functionality can be achieved using np.newaxis.

Copy

  • Return an array copy of the given object.
import numpy as np

a = np.array([[1, 2], [3, 4]])
b = a
c = np.copy(a)

a[0] = 10

print(a)     # Prints [[10 10]
             #         [ 3  4]]

a[0] == b[0] # Prints True
a[0] == c[0] # Prints False
  • Note that np.copy() performs a shallow copy and will not copy object elements within arrays. This is mainly important for arrays containing Python objects.

Element-wise sign

  • Returns an element-wise sign of an array’s elements.
import numpy as np

a = np.array([[1, 2], [-3, -4]])

print(np.sign(a)) # Prints [[ 1  1]
                  #         [-1 -1]]

Sum

  • Sum of an array’s elements.
import numpy as np

a = np.array([[1, 2], [3, 4]])

# Compute sum of each column
print(np.sum(a, axis=0)) # Prints [4 6]

# Compute sum of each row
print(np.sum(a, axis=1)) # Prints [3 7]
  • The axis argument specifies the axis along which the sum is performed. If axis is a tuple of ints, a sum is performed on all of the axes specified in the tuple instead of a single axis or all the axes as before.
  • Note that np.sum() yields an array with the same shape as the original array with the specified axis removed (which implies that if you sum over the rows in a 2D matrix, you get as many entries in the output as the number of columns and vice versa).
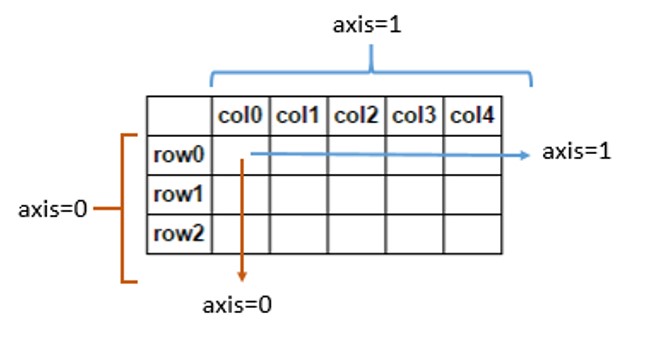
  • In the above example, since axis=0 refers to the rows of the input matrix, np.sum() sums over all rows and in other words, computes the sum of each column.
  • As a visual description here’s how np.sum() works under the hood (the arrows indicate the flow of summation for axis=0 or axis=1):

  • If axis isn’t specified, it defaults to None, in which case np.sum() sums over all of the elements of the input array:
import numpy as np

a = np.array([[1, 2], [3, 4]])

# Compute sum of all elements
print(np.sum(a)) # Prints 10
  • Some examples of np.sum():
a = np.array([[1, 0], [0, 1]])

# Count number of 1s in the input array
print(np.sum(a)) # Prints 2

b = np.array([[1, 2], [2, 1]])

# Count number of 1s in the input array
print(np.sum(b == 1)) # Prints 2

Average/Mean

  • Recall that the mean is the sum of the elements divided by the length of the vector.
import numpy as np

a = np.array([[1, -1], [2, -2], [3, -3]]) # Define a 3x2 matrix. Chosen to be a matrix with 0 mean.

# Get the mean for the whole matrix
print(np.mean(a)) # Prints 0.0

# Get the mean for each column. Returns 2 elements.
print(a, axis=0)  # Prints [ 2. -2.]

# Get the mean for each row. Returns 3 elements.
print(a, axis=1)  # Prints [0. 0. 0.]

Product

  • Return the product of array elements over a given axis.
import numpy as np

a = np.array([[1, 2], [3, 4]])

print(np.prod(a)) # Prints 24

Len

  • len() returns the size of the first dimension of the input tensor, similar to PyTorch.
import numpy as np

a = np.array([[1, 2], [3, 4]])
print(a) # Prints [[1, 2],
         #         [3, 4]]
len(a)   # 2

b = np.array([1, 2, 3, 4])
print(b) # Prints [1 2 3 4]
len(b)   # 4

Dot Product

  • Refer to the earlier section on dot product to learn the usage of np.dot(). Note that the dot product (also called the inner/scalar product) yields a scalar.

Outer Product

  • Return the outer product of two vectors. Note that the outer product yields a vector.
import numpy as np

a = np.ones((5,))
b = np.linspace(-2, 2, 5)

print(np.outer(a, b)) 
# Prints:
# [[-2. -1.  0.  1.  2.]
#  [-2. -1.  0.  1.  2.]
#  [-2. -1.  0.  1.  2.]
#  [-2. -1.  0.  1.  2.]
#  [-2. -1.  0.  1.  2.]]

Matrix Product

  • Return matrix product of two arrays.
  • The following rules dictate the behavior of np.matmul() depending on the arguments:
    • If both arguments are 2D, they are multiplied like conventional matrices.
    • If either argument is N-dimensional (with \(N > 2\)), it is treated as a stack of matrices residing in the last two indexes and broadcast accordingly.
    • If the first argument is 1D (while the second is N-dimensional, where \(N \geq 2\)), it is promoted to a matrix by prepending a 1 to its dimensions. After matrix multiplication, the prepended 1 is removed.
    • If the second argument is 1D (while the second is N-dimensional, where \(N \geq 2\)), it is promoted to a matrix by appending a 1 to its dimensions. After matrix multiplication, the appended 1 is removed.
import numpy as np

# For 2D arrays, np.matmul() is the conventional matrix product.
a = np.array([[1, 0], [0, 1]])
b = np.array([[4, 1], [2, 2]])

print(np.matmul(a, b)) # Prints [[4 1]
                       #         [2 2]]

# For 2D mixed with 1D, the result is the usual., np.matmul() is the conventional matrix product.
a = np.array([[1, 0], [0, 1]])
b = np.array([1, 2])

# The output matrices below are both 1D after the removal of the appended/prepended 1 dimension
print(np.matmul(a, b)) # Prints [1 2]
print(np.matmul(b, a)) # Prints [1 2]

np.matmul() vs. np.dot()

  • np.matmul() differs from np.dot() in two important ways:
    • Multiplication by scalars is not allowed, use * instead.
    • Stacks of matrices (i.e., tensors) are broadcast together as if the matrices were elements, respecting the signature \((n, k) \times (k, m) \rightarrow (n, m)\):
import numpy as np

a = np.ones([9, 5, 7, 4])
c = np.ones([9, 5, 4, 3])
print(np.dot(a, c).shape)    # Prints (9, 5, 7, 9, 5, 3)
print(np.matmul(a, c).shape) # Prints (9, 5, 7, 3) / n is 7, k is 4, m is 3 per the stacked-matrices rule

Max

  • Return the maximum element of an array or maximum along an axis.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

print(np.max(a)) # Prints 6

Element-wise max

  • Compare two compatible arrays and return their element-wise maximum. Here, ‘compatible’ means that one array can be broadcast to the other.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[7, 8, 9], [-2, -1, 0]])

print(np.maximum(a, b)) # Prints [[7 8 9]
                        #         [4 5 6]]

Argmax

  • Return the indices of the maximum values along an axis.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

print(np.argmax(a))         # Prints 5
print(np.argmax(a, axis=0)) # Prints [1 1 1]
print(np.argmax(a, axis=1)) # Prints [2 2]
  • Note that in case of multiple occurrences of the maximum values, only the index corresponding to the first occurrence is returned.

Argmin

  • Return the indices of the minimum values along an axis.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

print(np.argmin(a))         # Prints 0
print(np.argmin(a, axis=0)) # Prints [0 0 0]
print(np.argmin(a, axis=1)) # Prints [0 0]
  • Note that in case of multiple occurrences of the minimum values, only the index corresponding to the first occurrence is returned.

Where

  • np.where() accepts three arguments: (condition, x, y). If only the condition argument is supplied, np.where() simply returns the indicies of the elements in the input array which satisfy the condition:
a = np.array([[1, 0], [0, 1]])

print(np.where(c == 1)) # Print (array([0, 1]), array([0, 1]))
  • If all three arguments are supplied, it first evaluates the condition argument – if it returns True, it returns x, otherwise yields y.
import numpy as np

a = np.array([0, 1, 2, 3, 4, 5])

print(np.where(a < 3, a, 10*a)) # Prints [ 0  1  2 30 40 50]

Pad

  • Pad an array.
  • np.pad() accepts three arguments: array, pad_width, mode='constant'.
    • pad_width specifies the number of values padded to the edges of each axis. It accepts both an int and a tuple.
      • (pad,) or simply a pad (as an int) is a shortcut for before = after = pad width for all axes.
      • ((before_1, after_1), ... (before_N, after_N)) specifies the padding widths for each axis.
      • ((before, after),) yields same before and after padding width for each axis.
    • When mode is set to constant (which is the default), an optional parameter constant_values let’s you specify the padding values for each axis, which has a default of 0 (i.e., zero padding). Rather than just an int, constant_values accepts a tuple as well:
      • (constant,) or simply a constant (as an int) is a shortcut for before = after = constant for all axes. Default is 0.
      • ((before_1, after_1), ... (before_N, after_N)) specifies the unique pad constants for each axis.
      • ((before, after),) yields same before and after constants for each axis.
import numpy as np

a = np.array([1, 2, 3, 4, 5])
print(np.pad(a, 1, 'constant'))                              # Prints [0 1 2 3 4 5 0]
print(np.pad(a, (2, 3), 'constant', constant_values=(4, 6))) # Prints [4 4 1 2 3 4 5 6 6 6]

a = np.array([[1, 2], [3, 4]])
print(np.pad(a, 1, 'constant', constant_values=(4, 6)))      # Prints [[4 4 4 6]
                                                             #         [4 1 2 6]
                                                             #         [4 3 4 6]
                                                             #         [4 6 6 6]]

# With pad_width = [(0, 1), (0, 1)], each tuple item in the pad_width list 
# corresponds to a dimension and the item therein represents the padding 
# before (first element) and after (second element). Graphically,
# [(0, 1), (0, 1)]
#          ^^^^^^------ padding for second dimension
#  ^^^^^^-------------- padding for first dimension
# 
#   ^------------------ no padding at the beginning of the first axis
#      ^--------------- pad with one "value" at the end of the first axis.
a = np.ones(2, 2)
print(np.pad(a, [(0, 1), (0, 1)], mode='constant'))          # Prints [[1 2 0]
                                                             #         [3 4 0]
                                                             #         [0 0 0]]

# In this case the padding for the first and second axis are identical, 
# so one could also just pass in the 2-tuple.
print(np.pad(a, (0, 1), mode='constant'))                    # Prints [[1 2 0]
                                                             #         [3 4 0]
                                                             #         [0 0 0]]
                                                             
# In case the padding before and after is identical, one could even omit 
# the tuple (not applicable in this case though):
print(np.pad(a, 1, mode='constant'))                         # Prints [[0 0 0 0]
                                                             #         [0 1 2 0]
                                                             #         [0 3 4 0]
                                                             #         [0 0 0 0]]

# Or if the padding before and after is identical but different for the axis, you could also omit the second argument in the inner tuples:
print(np.pad(a, [(1, ), (2, )], mode='constant'))            # Prints [[0 0 0 0 0 0]
                                                             #         [0 0 1 2 0 0]
                                                             #         [0 0 3 4 0 0]
                                                             #         [0 0 0 0 0 0]]
  • However using the explicit pad_width specification should be preferred because it’s just to easy to make mistakes, as in the case below:
# Here NumPy thinks you wanted to pad all axis with 1 element before and 
# 2 elements after each axis! 
# Even if you intended it to pad with 1 element in axis 1 and 2 elements for axis 2.
print(np.pad(a, [1, 2], mode='constant')) # Prints [[0 0 0 0 0]
                                          #         [0 1 2 0 0]
                                          #         [0 3 4 0 0]
                                          #         [0 0 0 0 0]
                                          #         [0 0 0 0 0]]

Ravel

  • Return a contiguous flattened array.
  • Note that np.ravel() returns a view of the array when the elements are contiguous in memory (just like np.reshape()). So modifying the result of np.ravel() would also modify the original array. However, np.ravel() returns a copy if, say the input array were made from slicing another array using a non-unit step size (for e.g., a = x[::2]).
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
print(np.ravel(a)) # Prints [1 2 3 4 5 6]
  • Note that np.ravel() is equivalent to np.reshape(-1).
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
print(np.reshape(a, -1)) # Prints [1 2 3 4 5 6])

Unravel Index

  • Converts a “flat” index (i.e., an index into the flattened version of an array) into a tuple of coordinate arrays.
import numpy as np

# Passing an integer array whose elements are indices into the flattened version of an array
print(np.unravel_index([1, 2, 3], [4, 5])) # Prints (array([0, 0, 0]), array([1, 2, 3]))

# You're not limited to the 2-dimensional XY co-ordinate space
print(np.unravel_index(7, (1, 1, 7)))     # Prints (0, 0, 6)

Internals

  • Computer memory is addressed linearly. Each memory cell corresponds to a number. A block of memory can be addressed in terms of a base, which is the memory address of its first element, and the item index. For example, assuming the base address is 10,000:
item index      0       1       2       3
memory address  10,000  10,001  10,002  10,003
  • To store multi-dimensional blocks, their geometry must somehow be made to fit into linear memory. In C and NumPy, this is done row-by-row (which is known as the row-major order). A 2D example would be:
     | 0      1      2      3
   --+------------------------
   0 | 0      1      2      3
   1 | 4      5      6      7
   2 | 8      9     10     11
  • So, for example, in this 3-by-4 block the 2D index \((1, 2)\) would correspond to the linear index 6 which is \(1 \times 4 + 2\). In general, the linear index is given by: \(\text{row index }\times\text{row length }+\text{ column index}\).
  • np.unravel_index() does the inverse. Given a linear index, it computes the corresponding coordinates. Since this depends on the block dimensions, these also have to be passed. So, in our example, we can get the original 2D index \((1, 2)\) back from the linear index 6: np.unravel_index(6, (3, 4))) # Prints (1, 2)

Exponential

  • Calculate the exponential of all elements in the input array.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

print(np.exp(a)) # Prints [[   2.71828183    7.3890561    20.08553692]
                 #         [  54.59815003  148.4131591   403.42879349]]

Unique

  • Find the unique elements of an array.
import numpy as np

a = np.array([[1, 1, 1], [2, 2, 2]])

print(np.unique(a)) # Prints [1 2]
  • np.unique() supports an optional return_index argument which returns the indices with unique elements in addition to the unique elements.
import numpy as np

a = np.array([[1, 1, 1], [2, 2, 2]])

unique_els, indices = np.unique(a, return_index=True)
unique_els # Prints array([1, 2])
indices    # Prints array([0, 3])
  • np.unique() also supports an optional return_counts argument which returns the counts corresponding to the unique elements in addition to the unique elements.
import numpy as np

a = np.array([[1, 1, 1], [2, 2, 2]])

unique_els, counts = np.unique(a, return_counts=True)
unique_els # Prints array([1, 2])
counts     # Prints array([3, 3])

Bincount

  • Count number of occurrences of each value in a one-dimensional array of non-negative integers.
import numpy as np

a = np.array([1, 1, 1, 2, 2, 2])

print(np.bincount(a)) # Prints [0 3 3]

Element-wise square

  • Return the element-wise square of the input.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])

print(np.square(a)) # Prints [[ 1   4  9]
                    #         [[16 25 36]]

Element-wise square root

  • Return the element-wise non-negative square root of an array.
import numpy as np

a = np.array([[1, 4, 9], [16, 25, 36]])

print(np.sqrt(a)) # Prints [[1. 2. 3.]
                  #         [4. 5. 6.]]

Split

  • Split an array into multiple sub-arrays.
import numpy as np

a = np.arange(8)

print(np.split(a, 2)) # Prints [array([0, 1, 2, 3]), array([4, 5, 6, 7])]

Swapaxes

  • Interchange two axes of an array.
import numpy as np

a = np.zeros((2, 3, 5))
print(a.shape)                     # Prints (2, 3, 5)

print(np.swapaxes(a, 0, -1).shape) # Prints (5, 3, 2)

Moveaxis

  • Compared to np.transpose() for reordering axes which needs positions of all axes to be explicitly specified, moving one axis while keeping the relative positions of all others is a common enough use-case to warrant its own syntactic sugar. This is the functionality that is offered by np.moveaxis().
import numpy as np

a = np.zeros((2, 3, 5))
print(a.shape)                     # Prints (2, 3, 5)

print(np.moveaxis(a, 0, -1).shape) # Prints (3, 5, 2)

Horizontal split

  • Split an array into multiple sub-arrays horizontally (column-wise).
  • Note that np.hsplit() is equivalent to np.split with axis=1. Put simply, with np.hsplit(), the array is always split along the second axis regardless of the array dimension.
import numpy as np

a = np.arange(4).reshape(2, 2)

print(a)               # Prints [[0 1]
                       #         [2 3]]

print(np.hsplit(a, 2)) # Prints [array([[0],
                       #                [2]]),
                       #        [array([[1],
                       #                [3]])]

Vertical split

  • Split an array into multiple sub-arrays vertically (row-wise).
  • Note that np.vsplit() is equivalent to np.split with axis=0 (which is the default for np.split). Put simply, with np.vsplit(), the array is always split along the second axis regardless of the array dimension.
import numpy as np

a = np.arange(4).reshape(2, 2)

print(a)               # Prints [[0 1]
                       #         [2 3]]

print(np.vsplit(a, 2)) # Prints [array([[0, 1]]), array([[2, 3]])]

# np.split() with axis=0 (which is the defauly) yields the same output as np.vsplit()
print(np.split(a, 2))  # Prints [array([[0, 1]]), array([[2, 3]])]

Append

  • Append values to the end of an array. If the axis argument is not given, both the input array and values are flattened before use.
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[7, 8, 9]])

print(np.append(a, b))         # Prints [1 2 3 4 5 6 7 8 9]
print(np.append(a, b, axis=0)) # Prints [[1 2 3]
                               #         [4 5 6]
                               #         [7 8 9]]
  • As another example:
a = np.arange(4).reshape(2, 2) # Prints [[0 1]
                               #         [2 3]]
print(np.append(a, a))         # Prints [0 1 2 3 0 1 2 3]
print(np.append(a, a, axis=0)) # Prints [[0 1]
                               #         [2 3]
                               #         [0 1]
                               #         [2 3]]
  • With np.append(), it is important to note that both input arrays must have the same shape. However, if axis is not specified, the input arrays can be any shape (since they will be flattened before use).
import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([7, 8, 9])

print(np.append(a, b, axis=0)) # ValueError: all the input arrays must have same number of dimensions
print(np.append(a, b))         # Prints [1 2 3 4 5 6 7 8 9]

Stack

  • Join a sequence of arrays along a new axis.
  • The axis parameter specifies the index of the new axis in the dimensions of the result. For e.g., axis=0 denotes the first dimension and axis=-1 denotes the last dimension. Note that by default, axis is set to 0.
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

print((a, b))                   # Prints (array([1, 2, 3]), array([4, 5, 6]))

print(np.stack((a, b)))         # Prints [[1 2 3]
                                #         [4 5 6]]

# This is the same as above since axis is set to 0 by default
print(np.stack((a, b), axis=0)) # Prints [[1 2 3]
                                #         [4 5 6]]
  • For the given input arrays a and b, note that np.vstack() command yields the same output as np.stack(), since np.vstack() simply stacks them vertically (row-wise) thereby implicitly creating a new dimension (since the input arrays are 1D and cannot be stacked without adding a dimension), while np.stack() adds a new dimension at index 0 explicitly and stacks them along that dimension.
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# This is the same as above since axis is set to 0 by default
print(np.stack((a, b), axis=0)) # Prints [[1 2 3]
                                #         [4 5 6]]

# np.vstack() yields the same output as np.stack()
# Note that np.vstack() is discussed in more detail below
print(np.vstack((a, b)))        # Prints [[1 2 3]
                                #         [4 5 6]]
  • For the given input arrays a and b, note that np.vstack() yields an output dissimilar to np.stack(), since np.vstack() simply stacks them vertically (row-wise), while np.stack() adds a new dimension at index 0 explicitly and stacks them along that dimension.
import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

c = np.stack((a, b))
print(c)       # Prints [[[1 2]
               #          [3 4]]
               #        
               #         [[5 6]
               #          [7 8]]]
print(c.shape) # Prints (2, 2, 2)

d = np.vstack((a, b))
print(d)       # Prints [[1 2]
               #         [3 4]
               #         [5 6]
               #         [7 8]]
print(d.shape) # Prints (4, 2)
  • Joining arrays column-wise by doing horizontal stacking:
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

print(np.stack((a, b), axis=1)) # Prints [[1 4]
                                #         [2 5]
                                #         [3 6]]

# Note np.hstack() does *not* match the output of np.stack()
print(np.hstack((a, b)))        # Prints [1 2 3 4 5 6]
  • With np.stack(), it is important to note that all input arrays must have exactly the same shape. Specifically, not only do the input arrays need to have the same number of dimensions (i.e., equal ranks), but also all the dimensions themselves should be equal-length. This is an important point of differentiation compared to np.vstack() and np.hstack() (which require only the concatenation axis to be equal-length).
import numpy as np

a = np.array([[[1, 2]]])
b = np.array([[3, 4]])

print(np.stack((a, b)))  # ValueError: all input arrays must have the same shape

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])

print(np.stack((a, b)))  # ValueError: all input arrays must have the same shape
print(np.vstack((a, b))) # Prints [[1 2]
                         #         [3 4]
                         #         [5 6]]
  • For arrays of rank \(\geq 2\) (i.e., tensors), np.stack() works well too:
import numpy as np

arrays = [np.random.randn(3, 4) for _ in range(10)]
np.stack(arrays, axis=0).shape # Prints (10, 3, 4)
np.stack(arrays, axis=1).shape # Prints (3, 10, 4)
np.stack(arrays, axis=2).shape # Prints (3, 4, 10)

Vertical stack

  • Stack arrays in sequence vertically (row-wise for 2D arrays). In general, for arrays of rank \(\geq 2\) (i.e., tensors), stack arrays along the first dimension.
  • Note that np.vstack() does not accept an axis argument.
  • np.vstack() is equivalent to np.concatenate(<ndarray>, axis=0) along the first axis (after 1D arrays of shape (N,) have been reshaped to (1, N)).
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

print(np.vstack((a, b))) # Prints [[1 2 3]
                         #         [4 5 6]]
                         
a = np.array([[1], [2], [3]])
b = np.array([[4], [5], [6]])

print(np.vstack((a, b))) # Prints [[1]
                         #         [2]
                         #         [3]
                         #         [4]
                         #         [5]
                         #         [6]]
  • With np.vstack(), it is important to note that all input arrays must have:
    • The same number of dimensions (i.e., equal ranks), and
    • Equal-length concatenation axes (in the case of 2D arrays, their respective second dimensions must be equal-length, i.e., the same number of columns). This is an important point of differentiation compared to np.stack() and np.hstack().
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])

print(np.vstack((a, b))) # Prints [[1 2]
                         #         [3 4]
                         #         [5 6]]
                         
a = np.array([[[1, 2]]])
b = np.array([[3, 4]])

print(np.vstack((a, b))) # ValueError: all the input arrays must have same number of dimensions

a = np.array([1, 2, 3])
b = np.array([4, 5])

print(np.vstack((a, b))) # ValueError: all the input array dimensions for the concatenation axis must match exactly
  • For arrays of rank \(\geq 2\) (i.e., tensors), np.vstack() works well too:
a = np.array([[[1, 2]]])
b = np.array([[[3, 4]]])
print(a.shape) # Prints (1, 1, 2)

c = np.vstack((a, b))
print(c)       # Prints [[[1 2]]
               #         [[3 4]]]

print(c.shape) # Prints (2, 1, 2)

Horizontal stack

  • Stack arrays in sequence horizontally (column-wise for 2D arrays). In general, for arrays of rank \(\geq 2\) (i.e., tensors), stack arrays along the second dimension.
  • Note that np.hstack() does not accept an axis argument.
  • np.hstack() is equivalent to np.concatenate(<ndarray>, axis=1), except for 1D arrays where it concatenates along the first axis.
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

print(np.hstack((a, b))) # Prints [1 2 3 4 5 6]

a = np.array([[1], [2], [3]])
b = np.array([[4], [5], [6]])

print(np.hstack((a, b))) # Prints [[1 4]
                         #         [2 5]
                         #         [3 6]]
  • With np.hstack(), it is important to note that all input arrays must have:
    • The same number of dimensions (i.e., equal ranks), and
    • Equal-length concatenation axes (in the case of 2D arrays, their respective first dimensions must be equal-length, i.e., the same number of rows). This is an important point of differentiation compared to np.stack() and np.vstack().
a = np.array([1, 2, 3])
b = np.array([4, 5])

print(np.hstack((a, b))) # Prints [1 2 3 4 5]

a = np.array([[[1, 2]]])
b = np.array([[3, 4]])

print(np.hstack((a, b))) # ValueError: all the input arrays must have same number of dimensions

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])

print(np.hstack((a, b))) # ValueError: all the input array dimensions for the concatenation axis must match exactly
  • For arrays of rank \(\geq 2\) (i.e., tensors), np.hstack() works well too:
a = np.array([[[1, 2]]])
b = np.array([[[3, 4]]])
print(a.shape) # Prints (1, 1, 2)

c = np.hstack((a, b))
print(c)       # Prints [[[1 2]
               #          [3 4]]]

print(c.shape) # Prints (1, 2, 2)

Column Stack

  • Take a sequence of 1D arrays and stack them as columns to make a single 2D array. 2D arrays are stacked as-is, just like with np.hstack. 1D arrays are turned into 2D column vectors first.
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

print(np.column_stack((a, b)))                       # Prints [[1 4]
                                                     #         [2 5]
                                                     #         [3 6]]
                               
# The following np.stack() and np.hstack() commands 
# return the same output as well
print(np.stack((a, b), axis=1))                      # Prints [[1 4]
                                                     #         [2 5]
                                                     #         [3 6]]
print(np.hstack(([[1], [2], [3]], [[4], [5], [6]]))) # Prints [[1 4]
                                                     #         [2 5]
                                                     #         [3 6]]
  • Note that np.column_stack() is equivalent to np.vstack().T:
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# np.vstack().T returns the same output as np.column_stack()                               
print(np.vstack((a, b)).T) # Prints [[1 4]
                           #         [2 5]
                           #         [3 6]]

Concatenate

  • Join a sequence of arrays along an existing axis.
  • The axis argument specifies the axis along which the arrays will be joined. If axis is None, the arrays are flattened before use. The default is 0 (vertical/row-wise stacking).
  • Joining arrays row-wise by doing vertical stacking:
import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])

print(np.concatenate((a, b)))         # Prints [[1 2]
                                      #         [3 4]
                                      #         [5 6]]
                                      
# The following np.vstack() command returns the same output
print(np.vstack((a, b)))              # Prints [[1 2]
                                      #         [3 4]
                                      #         [5 6]]
  • Joining arrays column-wise by doing horizontal stacking:
print(np.concatenate((a, b.T), axis=1)) # Prints [[1 2 5]
                                        #         [3 4 6]]
                                         
# The following np.hstack() and np.column_stack() command 
# return the same output as well
print(np.hstack((a, b.T)))              # Prints [[1 2 5]
                                        #         [3 4 6]]
                                         
print(np.column_stack((a, b.T)))        # Prints [[1 2 5]
                                        #         [3 4 6]]
  • Joining arrays after flattening them:
print(np.concatenate((a, b), axis=None)) # Prints [1 2 3 4 5 6]

# The following np.append() command returns the same output as well
print(np.append(a, b))                   # Prints [1 2 3 4 5 6]

Concatenate vs. hstack/vstack vs. append vs. column_stack

  • All the aforementioned functions, except np.concatenate(), are written in Python and work by tweaking the dimensions of the input arrays, and then concatenating on the right axis. In other words, they are convenience functions since they’re just wrappers around np.concatenate(). Here’s a summary of their code:
vstack:
# Turn all inputs into 2D (or more) and concatenate on first dimension
concatenate([atleast_2d(_m) for _m in tup], axis=0) 
# Equivalent to np.concatenate(tup, axis=0) if input tuple contains arrays that are at least 2D

hstack:
concatenate([atleast_1d(_m) for _m in tup], axis=<0 or 1>)

column_stack:
if needed, transform arrays using array(arr, copy=False, subok=True, ndmin=2).T
concatenate([atleast_1d(_m) for _m in tup], axis=1)

append:
concatenate((asarray(arr), values), axis=axis)
  • As a side note, with an IPython shell you can use ?? to query the source code of a particular function.

Graphical treatment

  • If you have two matrices, np.hstack() stacks horizontally while np.vstack() stacks vertically:

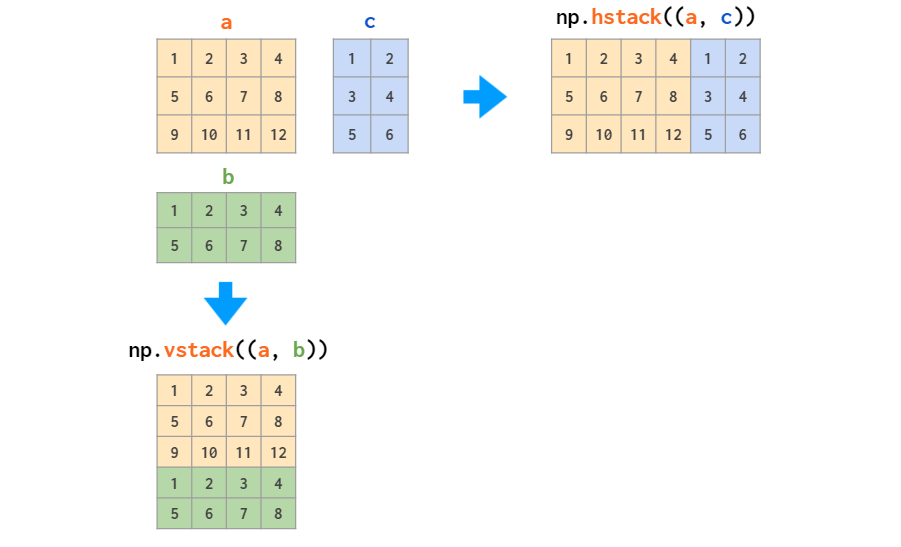
  • If you’re stacking a matrix and a vector, np.hstack() becomes tricky to use, so np.column_stack() is a better option. The problem with np.hstack() is that when you append a column, you need convert it from a 1D array to a 2D column vector first, because a 1D array is normally interpreted as a row vector in 2D context in NumPy:
a = np.ones(2)       # 2D, shape = (2, 2)
b = np.array([0, 0]) # 1D, shape = (2,)

np.hstack((a, b))    # Dimensions mismatch error

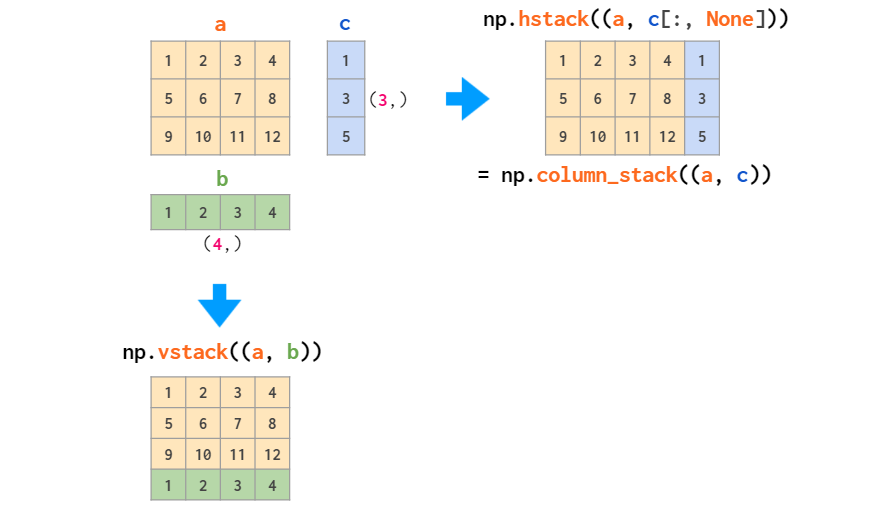
  • If you’re stacking two vectors, you’ve got three options:

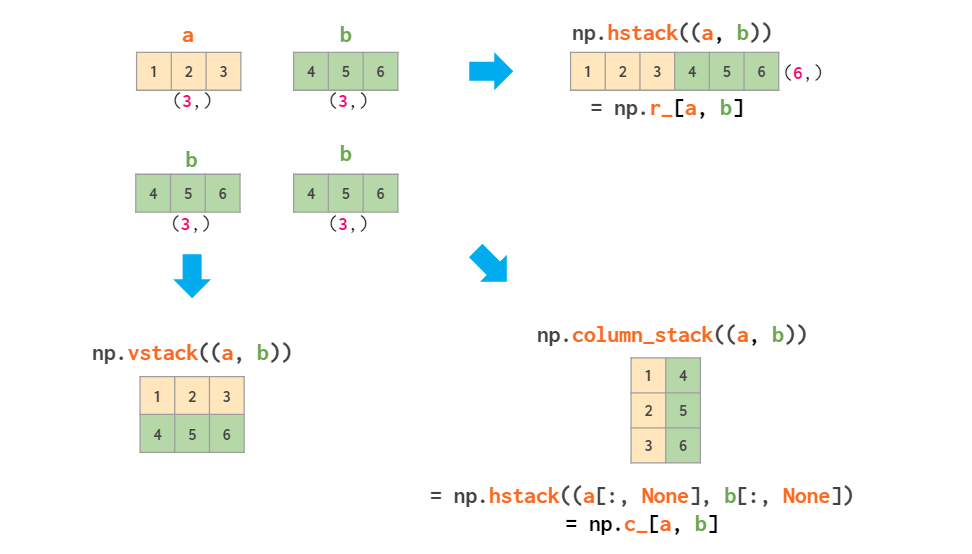
  • np.concatenate() in its raw form is useful for 3D arrays and above (i.e., tensors).

New axis

  • np.newaxis is used to increase the dimension of the existing array by an additional dimension, for e.g., a 1D array gets transformed to a 2D array, a 2D array gets transformed to a 3D array, and so on.
  • Essentially,np.newaxis is a pseudo-index that allows the temporary addition of an axis into a multiarray.
  • Here is a visual illustration which depicts the promotion of a 1D array to a 2D array (row/column vector):

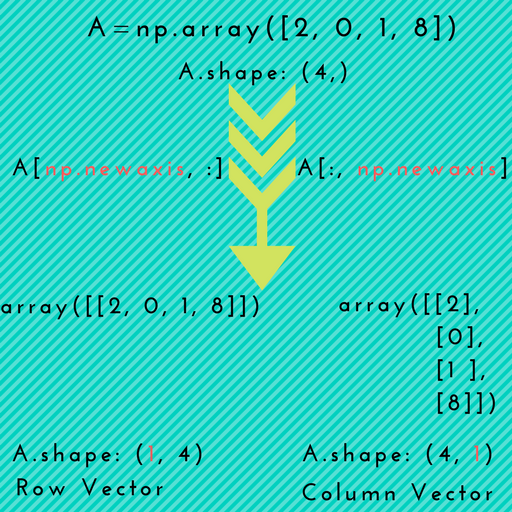
Usecase: 1D array -> 2D vector

  • np.newaxis might come in handy when you wish to explicitly convert a 1D array to either a 2D row or a column vector, as depicted in the above picture. The section on Transpose also describes this usecase. As an example:
# Define a 1D array
a = np.arange(4)
a.shape                    # Prints (4,)

# Make "a" a row vector by inserting an axis along the first dimension
row_vec = a[np.newaxis, :] # or a[None, :]
row_vec.shape              # Prints (1, 4)

# Make "a" a column vector by inserting an axis along the second dimension
col_vec = a[:, np.newaxis] # or arr[:, None]
col_vec.shape              # Prints (4, 1)

Usecase: During broadcasting

  • When making use of broadcasting as part of some operation, for instance while doing addition of some arrays, np.newaxis proves useful by inserting a new dimension with size 1 (which is one of the required conditions for broadcasting to work). As an example, let’s say you want to add the following two arrays:
import numpy as np

a = np.array([1, 2, 3, 4, 5])
b = np.array([5, 4, 3])
  • If you try to add these 1D arrays just like that, NumPy will raise the following ValueError:
# ValueError: operands could not be broadcast together with shapes (5,) (3,)
  • To remedy this, you can use np.newaxis to increase the dimension of one of the arrays so that NumPy can broadcast:
# Let's utilize np.newaxis with a
a_new = a[:, np.newaxis] # or a[:, None]
a_new.shape              # Prints (5, 1)
print(a_new)             # Prints [[1]
                         #         [2]
                         #         [3]
                         #         [4]
                         #         [5]]

# Now, add
print(a_new + b)         # Prints [[ 6  5  4]
                         #         [ 7  6  5]
                         #         [ 8  7  6]
                         #         [ 9  8  7]
                         #         [10  9  8]]

# Alternatively, you can also utilize np.newaxis with b
b_new = b[:, np.newaxis] # or b[:, None]
b_new.shape              # Prints (3, 1)
print(b_new)             # Prints [[5]
                         #         [4]
                         #         [3]]

# Now, add
print(a + b_new)         # Prints [[ 6  7  8  9 10]
                         #         [ 5  6  7  8  9]
                         #         [ 4  5  6  7  8]]

# Note that we get the same result in both cases (but one being the transpose of the other)
  • In the example below, we inserted a temporary axis using np.newaxis between the first and second axes of B to enable broadcasting.
import numpy as np

a = np.ones((3, 4, 5, 6))
b = np.ones((4, 6))

print((a + b[:, np.newaxis, :]).shape) # Prints (3, 4, 5, 6)
# or b[:, None, :]

Usecase: Promote to higher dimensions

  • This is similar to Usecase: 1D array -> 2D vector with the only exception being that this usecase involves repeated use of np.newaxis more than once to promote the input array to higher dimensions. Such an operation is sometimes needed for higher order arrays (i.e. Tensors).
import numpy as np

a = np.arange(5*5).reshape(5,5)
a.shape      # Prints (5, 5)

# Promoting 2D array to a 5D array
arr_5D = a[np.newaxis, ..., np.newaxis, np.newaxis] # or a[None, :, None, None]

arr_5D.shape # Prints (1, 5, 5, 1, 1)

np.newaxis vs. np.reshape()

  • np.newaxis uses the slicing operator to recreate the array while np.reshape() reshapes the array to the desired layout (assuming that the dimensions match; which is a must for a reshape to happen).
  • Using np.reshape(), we can achieve a similar end result as with np.newaxis:
import numpy as np

a = np.array([1, 2, 3])
print(a.shape)                              # Print (3,)
# Transform the 1D array to a row vector by reshaping with (1, -1), i.e., 1 row and 3 columns
print(a.reshape(1, -1).shape)               # Prints (1, 3)

a = np.array([1, 2, 3])
# Both of the np.newaxis commands yield the same output
print(a[np.newaxis, ...].shape)             # Prints (1, 3)
print(a[np.newaxis, :].shape)               # Prints (1, 3)

a = np.array([1, 2, 3])
# Transform the 1D array to a column vector by reshaping with (-1, 1), i.e., 3 rows and 1 column
print(a.reshape(-1, 1).shape)               # Prints (3, 1)

a = np.array([1, 2, 3])
# Both of the np.newaxis commands yield the same output
print(a[..., np.newaxis].shape)             # Prints (3, 1)
print(a[:, np.newaxis].shape)               # Prints (3, 1)

b = np.array([[1, 2, 3], [4, 5, 6]])
print(b.shape)                              # Print (2, 3)
# Transform the input array to dimensions (1, 2, 3, 1)
print(b.reshape(1, 2, 3, 1).shape)          # Prints (1, 2, 3, 1)

b = np.array([[1, 2, 3], [4, 5, 6]])
# Transform the input array to dimensions (1, 2, 3, 1)
print(b[np.newaxis, ..., np.newaxis].shape) # Prints (1, 2, 3, 1)

None as a shortcut for np.newaxis

  • You can also use None in place of np.newaxis; these are in fact the same objects.
np.newaxis is None # Prints True

Expand dims

  • As an alternative to np.newaxis, you can use np.expand_dims():
import numpy as np

a = np.arange(5*5).reshape(5,5)

# Use np.expand_dims to add an axis at index position 1
b = np.expand_dims(a, axis=1)
print(b.shape) # Prints (6, 1)

# Use np.expand_dims to add an axis at index position 0
c = np.expand_dims(a, axis=0)
print(c.shape) # Prints (1, 6)

# Using the intuitive `axis` argument to add new axes at the 
# 1st, 4th, and last (-1) dimension of the resulting array
arr_5D = np.expand_dims(a, axis=(0, 3, -1))
arr_5D.shape   # Prints (1, 5, 5, 1, 1)

Inverse

  • Compute the inverse of a matrix.
import numpy as np
from numpy.linalg import inv

a = np.array([[1., 2.], [3., 4.]])

print(inv(a)) # Prints [[-2.   1. ]
              #         [ 1.5 -0.5]]

Solve

  • Solve a linear matrix equation, or system of linear scalar equations.
import numpy as np
from numpy.linalg import solve

# Solve the system of equations:
# x0 + 2 * x1 = 1
# 3 * x0 + 5 * x1 = 2
a = np.array([[1, 2], [3, 5]])
b = np.array([1, 2])

print(np.linalg.solve(a, b)) # Prints [-1.  1.]

Test any

  • Test whether any array element along a given axis evaluates to True.
  • Returns a single boolean unless axis is not None (which is the default).
  • Note that not a number (NaN), \(\infty\) and \(-\infty\) all evaluate to True because these are not equal to 0.
import numpy as np

a = [[True, False], [True, True]]
print(np.any(a))                         # Prints True

a = [[True, False], [True, True]]
print(np.any(a, axis=0))                 # Prints [ True, True]

a = np.array([[1, 2], [3, 4]])
print(np.any(a))                         # Prints True

# A nifty use-case of np.any() is to select elements that satisfy 
# atleast one condition from multiple given conditions
a = np.array([[1, 2], [3, 4]])
print(np.any([a > 1, a < 5], axis=0))    # Prints [[ True  True]
                                         #         [ True  True]]
print(a[np.any([a > 1, a < 5], axis=0)]) # Prints [1 2 3 4]

# If axis is None (default), np.any() yields a single boolean by performing 
# a logical OR reduction over all the dimensions of the input array
print(np.any([a > 1, a < 5]))            # Prints True

Test all

  • Test whether all array elements along a given axis evaluate to True.
  • Similar to np.any(), np.all() returns a single boolean unless axis is not None (which is the default).
  • Again, similar to np.any(), note that not a number (NaN), \(\infty\) and \(-\infty\) all evaluate to True because these are not equal to 0.
import numpy as np

a = [[True, False], [True, True]]
print(np.all(a))                         # Prints True

a = [[True, False], [True, True]]
print(np.all(a, axis=0))                 # Prints [ True, False]

a = np.array([[1, 2], [3, 4]])
print(np.all(a))                         # Prints True

# A nifty use-case of np.all() is to select elements that satisfy 
# all given conditions
a = np.array([[1, 2], [3, 4]])
print(np.all([a > 1, a < 5], axis=0))    # Prints [[False  True]
                                         #         [ True  True]]
print(a[np.all([a > 1, a < 5], axis=0)]) # Prints [2 3 4]

# Note that if only one condition is specified, np.any() and np.all() 
# are equivalent, and have identical outputs
print(a[np.any([a > 1], axis=0)])        # Prints [2 3 4]
print(a[np.all([a > 1], axis=0)])        # Prints [2 3 4]

# If axis is None (default), np.all() yields a single boolean by performing 
# a logical AND reduction over all the dimensions of the input array
print(np.all([a > 1, a < 5]))            # Prints False

Convert NumPy Array to Python List

  • <ndarray>.tolist() returns the NumPy array as a nested list of Python scalars.
import numpy as np

a = np.arange(9).reshape(3, 3)

a.tolist() # Prints [[0, 1, 2], [3, 4, 5], [6, 7, 8]]

References

Further Reading

Here are some (optional) link(s) you may find interesting:

Citation

If you found our work useful, please cite it as:

@article{Chadha2020NumPyPrimer,
  title   = {NumPy Primer},
  author  = {Chadha, Aman},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}