Primers • Skip Connections
- Introduction
- The vanishing gradient problem
- Prelude: Backpropagation
- Backpropagation and partial derivatives
- Skip connections for the win
- ResNet: skip connections via addition
- DenseNet: skip connections via concatenation
- Short and Long skip connections in Deep Learning
- Case Study for long skip connections: U-Nets
- Conclusion
- Related Papers
- References
- Citation
Introduction
-
In order to understand the plethora of design choices involved in building deep neural nets (such as skip connections) that you see in so many works, it is critical to understand a little bit of the mechanisms of backpropagation.
-
If you were trying to train a neural network back in 2014, you would definitely observe the so-called vanishing gradient problem. In simple terms: you are behind the screen checking the training process of your network and all you see is that the training loss stopped decreasing but your performance metric is still far away from the desired value. You check all your code lines to see if something was wrong all night and you find no clue. Not the best experience in the world, believe me! Wonder why? Because the gradients that facilitate learning weren’t propagating through all the way to the initial layers of the network! Hence leading to “vanishing gradients”!
The vanishing gradient problem
-
So, let’s remind ourselves the update rule of gradient descent without momentum, given \(L\) to be the loss function and \(\lambda\) the learning rate:
\[w_{new} = w_{current} - \alpha \cdot \frac{\partial L}{\partial w_{current}}\] -
What is basically happening is that you try to update the parameters by changing them with a small amount \(\alpha \cdot \frac{\partial L}{\partial w_{current}}\) that was calculated based on the gradient, for instance, let’s suppose that for an early layer the average gradient \(\frac{\partial L}{\partial w_{current}} = 1e-15\). Given a learning rate \(\alpha\) of \(1e-4\), you basically change the layer parameters by the product of the referenced quantities \((\alpha \cdot \frac{\partial L}{\partial w_{current}})\), which is \(1e-19\), and as such, implies little to no change to the weights. As a result, you aren’t actually able to train your network. This is the vanishing gradient problem.
Prelude: Backpropagation
-
One can easily grasp the vanishing gradient problem from the backpropagation algorithm. We will briefly inspect the backpropagation algorithm from the prism of the chain rule, starting from basic calculus to gain an insight on skip connections. In short, backpropagation is the “optimization-magic” behind deep learning architectures. Given that a deep network consists of a finite number of parameters that we want to learn, our goal is to iteratively optimize these parameters using the gradient of the loss function \(L\) with respect to the network’s parameters.
-
As you have seen, each architecture has some input (say an image) and produces an output (prediction). The loss function is heavily based on the task we want to solve. For now, what you need to know is the loss function is a quantitative measure of the distance between two tensors, that can represent an image label, a bounding box in an image, a translated text in another language etc. You usually need some kind of supervision to compare the network’s prediction with the desired outcome (ground truth).
-
So, the beautiful idea of backpropagation is to gradually minimize this loss by updating the parameters of the network. But how can you propagate the scalar measured loss inside the network? That’s exactly where backpropagation comes into play.
Backpropagation and partial derivatives
- In simple terms, backpropagation is about understanding how changing the weights (parameters) in a network impacts the loss function by computing the partial derivatives. For the latter, we use the simple idea of the chain rule, to minimize the distance in the desired predictions. In other words, backpropagation is all about calculating the gradient of the loss function while considering the different weights within that neural network, which is nothing more than calculating the partial derivatives of the loss function with respect to model parameters. By repeating this step many times, we will continually minimize the loss function until it stops reducing, or some other predefined termination criteria are met.
Chain rule
- The chain rule basically describes the gradient (rate of change) of a function with respect to some input variable. Let the function be the loss function \(z\) of a neural network, while \(x\) and \(y\) be parameters of the neural network, which are in turn functions of a previous layer parameter \(t\). Further, let \(f, g, h\) be different layers on the network that perform a non-linear operation on the input vector. As such,
- Using the chain rule of multi-variate calculus to express the gradient of \(z\) with respect to the input \(t\):
-
Interestingly, the famous algorithm does exactly the same operation but in the opposite way: it starts from the output \(z\) and calculates the partial derivatives of each parameter, expressing it only based on the gradients of the later layers.
-
It’s really worth noticing that all these values are often less than 1, independent of the sign. In order to propagate the gradient to the earlier layer’s, backpropagation uses multiplication of the partial derivatives (as in the chain rule). For every layer that we go backwards in the network, the gradient of the network gets smaller and smaller owing to multiplication of the upstream gradient with absolute value less than 1 to compute the downstream gradient at every layer (since \(\text{downstream gradient = local gradient }\times\text{ upstream gradient}\)).
Skip connections for the win
-
Skip connections are standard in many convolutional architectures. By using a skip connection, we provide an alternative path for the gradient (with backpropagation). It is experimentally validated that this additional paths are often beneficial for model convergence during training. As the name suggests, skip connections in deep architectures, skip some layer in the neural network and feed the output of one layer as the input to the next layers (instead of only the next one).
-
As previously explained, using the chain rule, we must keep multiplying terms with the error gradient as we go backwards. However, in the long chain of multiplication, if we multiply many things together that are less than one, then the resulting gradient will be very small. Thus, the gradient becomes very small as we approach the earlier layers in a deep architecture. In some cases, the gradient becomes zero, meaning that we do not update the early layers at all.
-
In general, there are two fundamental ways that one could use skip connections through different non-sequential layers:
- Addition as in residual architectures,
- Concatenation as in densely connected architectures.
-
Let’s first do a walk-through of skip connections via addition, which are commonly referred as residual skip connections.
ResNet: skip connections via addition
- The core idea is to backpropagate through the identity function, by just using a vector addition. Then the gradient would simply be multiplied by one and its value will be maintained in the earlier layers. This is the main idea behind Residual Networks (ResNets): they stack these skip residual blocks together, as shown in the figure below (image taken from the ResNet paper). We use an identity function to preserve the gradient.
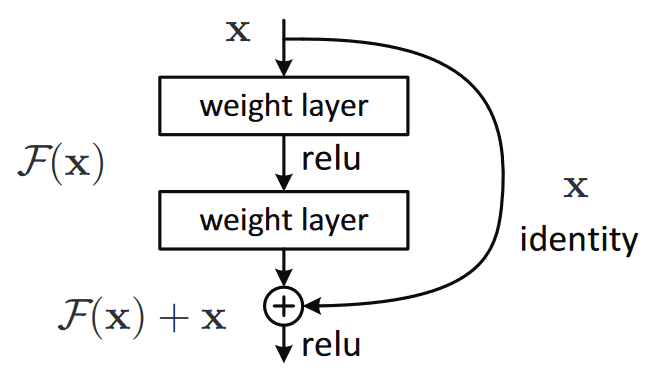
-
Mathematically, we can represent the residual block, and calculate its partial derivative (gradient), given the loss function like this:
\[\frac{\partial L}{\partial x } = \frac{\partial L}{\partial H} \frac{\partial H}{\partial x} = \frac{\partial L}{\partial H} \left( \frac{\partial F}{\partial x} + 1 \right) = \frac{\partial L}{\partial H} \frac{\partial F}{\partial x} + \frac{\partial L}{\partial H}\]- where \(H\) is the output of the network snippet above and is given by \(F(x) + x\)
-
Apart from the vanishing gradients, there is another reason that we commonly use them. For a plethora of tasks (such as semantic segmentation, optical flow estimation, etc.) information captured in the initial layers could be utilized by the later layers for learning. It has been observed that in earlier layers the learned features correspond to low-level semantic information that is extracted from the input. Without skip connections, that information would have turned too abstract.
DenseNet: skip connections via concatenation
- As stated, for many dense prediction problems, there is low-level information shared between the input and output, and it would be desirable to pass this information directly across the net. The alternative way that you can achieve skip connections is by concatenation of previous feature maps. The most famous deep learning architecture is DenseNet. Below you can see an example of feature reusability by concatenation with five convolutional layers (image taken from DenseNet):
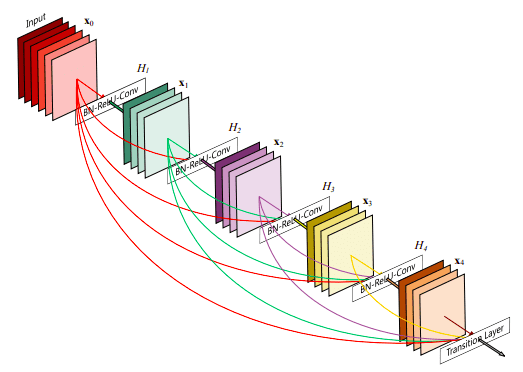
-
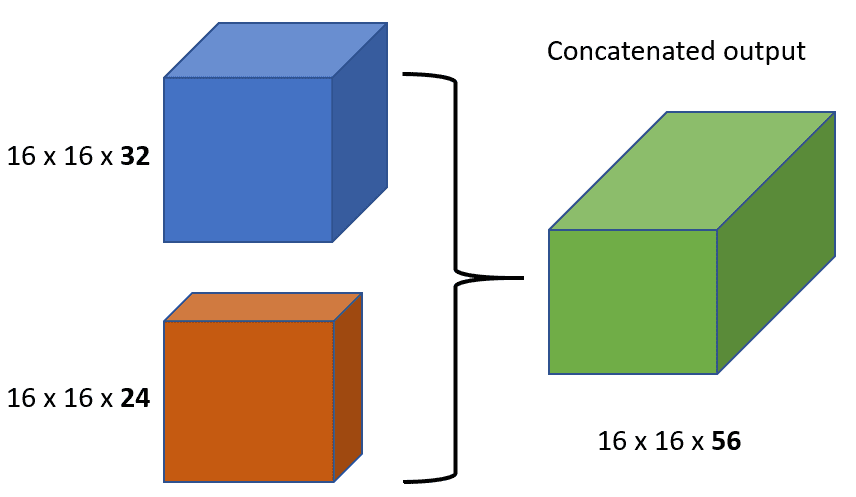
This architecture heavily uses feature concatenation so as to ensure maximum information flow between layers in the network. This is achieved by connecting via concatenation all layers directly with each other, as opposed to ResNets. Practically, what you basically do is to concatenate the feature channel dimension. This leads to:
-
An enormous amount of feature channels on the last layers of the network,
-
More compact models and,
-
Extreme feature re-usability.
-
Short and Long skip connections in Deep Learning
-
In more practical terms, you have to be careful when introducing additive skip connections in your deep learning model. The dimensionality has to be the same in addition and also in concatenation apart from the chosen channel dimension. That is the reason why you see that additive skip connections are used in two kinds of setups:
-
Short skip connections.
-
Long skip connections.
-
-
Short skip connections are used along with consecutive convolutional layers that do not change the input dimension (see ResNet), while long skip connections usually exist in encoder-decoder architectures. It is known that the global information (shape of the image and other statistics) resolves what, while local information resolves where (small details in an image patch).
-
Long skip connections often exist in architectures that are symmetrical, where the spatial dimension is gradually reduced in the encoder part and is gradually increased in the decoder part as illustrated below. In the decoder part, one can increase the dimensionality of a feature map via transpose convolutional (ConvT) layers. The transposed convolution operation forms the same connectivity as the normal convolution but in the backward direction.
Case Study for long skip connections: U-Nets
-
Mathematically, if we express convolution as a matrix multiplication, then transpose convolution is the reverse order multiplication (\(B \times A\) instead of \(A \times B\)). The aforementioned architecture of the encoder-decoder scheme along with long skip connections is often referred as U-shape (U-net). Long skip connections are utilized for tasks that the prediction has the same spatial dimension as the input such as image segmentation, optical flow estimation, video prediction, etc.
-
Long skip connections can be formed in a symmetrical manner, as shown in the diagram below:
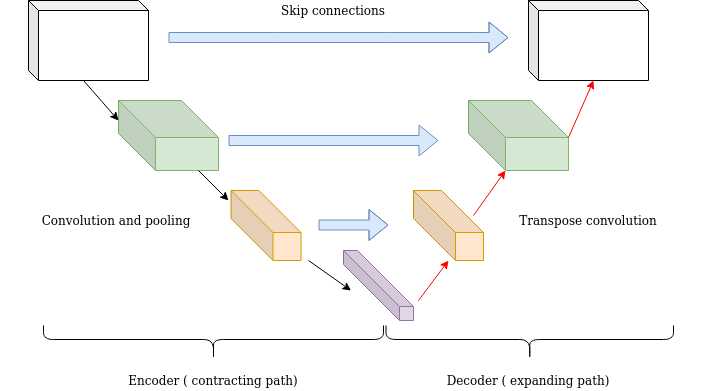
- By introducing skip connections in the encoder-decoded architecture, fine-grained details can be recovered in the prediction. Even though there is no theoretical justification, symmetrical long skip connections work incredibly effectively in dense prediction tasks (medical image segmentation).
Conclusion
-
To sum up, the motivation behind skip connections is that they enable an uninterrupted gradient flow during training, which helps tackle the vanishing gradient problem. Concatenative skip connections enable an alternative way to ensure feature reusability of the same dimensionality from the earlier layers and are widely used in symmetrical architectures.
-
On the other hand, long skip connections are used to pass features from the encoder path to the decoder path in order to recover spatial information lost during downsampling. Short skip connections appear to stabilize gradient updates in deep architectures. Overall, skip connections thus enable feature reusability and stabilize training and convergence.
-
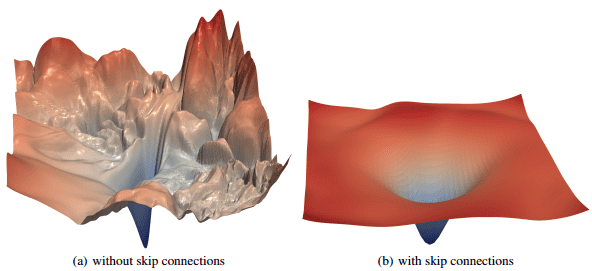
In “Visualizing the Loss Landscape of Neural Nets” by Li et al. (2017), it has been experimentally validated that the loss landscape changes significantly when introducing skip connections, as illustrated below:
Related Papers
Deep Residual Learning for Image Recognition
- ResNet paper by He et al. from Facebook AI in CVPR 2016. Most cited in several AI fields.
- The issue of vanishing gradients when training a deep neural network was addressed with two tricks:
- Batch normalization and,
- Short skip connections
- Instead of \(H(x) = F(x)\), the skip connection leads to \(H(x) = F(x) + x\), which implies that the model is learning the difference (i.e., residual), \(F(x) = H(x) - x\).
LAUREL: Learned Augmented Residual Layer
-
This paper by Gaurav Menghani, Ravi Kumar, and Sanjiv Kumar from Google Research introduces LAUREL (Learned Augmented Residual Layer), a generalization of the canonical residual connection used in deep learning architectures. LAUREL aims to improve model quality while keeping parameter, latency, and memory overhead minimal, making it suitable as a drop-in replacement in both vision and language models.
-
Core Concept:
- LAUREL extends the standard residual formulation: \(x_{i+1} = f(x_i) + x_i\) to a more expressive form: \(x_{i+1} = \alpha f(x_i) + g(x_i, x_{i-1}, ..., x_0)\) where $\alpha$ is a learnable scalar and $g(\cdot)$ is a learnable linear function over the current and previous layer outputs.
- The goal is to enhance the residual stream to support richer interactions and improved information propagation across layers.
-
Variants:
-
LAUREL-RW (Residual Weights): Introduces learnable weights $\alpha$ and $\beta$ for $f(x_i)$ and $x_i$ respectively: \(x_{i+1} = \alpha f(x_i) + \beta x_i\) Adds only two parameters per layer. Uses sigmoid or softmax to normalize $\alpha$, $\beta$.
-
LAUREL-LR (Low-Rank): Adds a low-rank linear transformation \(W = AB + I\) on \(x_i\): \(x_{i+1} = f(x_i) + B A x_i + x_i\) Reduces parameter growth using matrices $A, B \in \mathbb{R}^{D \times r}$ where $r \ll D$, leading to 2rD new parameters per layer.
-
LAUREL-PA (Previous Activations): Incorporates previous $k$ activations: \(x_{i+1} = f(x_i) + \left( \sum_{j=0}^{k-1} \gamma_{i,j} h_i(x_{i-j}) \right) + x_i\) Adds \(2rD + k\) parameters when using low-rank transforms for $h_i$. Supports richer temporal residual interactions.
-
These can be mixed into hybrid variants like LAUREL-RW+LR or LAUREL-RW+LR+PA, allowing flexibility in trade-offs between expressiveness and cost.
-
-
Implementation and Performance:
-
ResNet-50 on ImageNet-1K:
- Baseline: 74.95% top-1 accuracy.
- Adding one ResNet layer: 75.20% (+4.37% params).
- LAUREL-RW: 75.10% (+0.003% params).
- LAUREL-RW+LR (r=16): 75.20% (+1.68% params).
- LAUREL-RW+LR+PA: 75.25% (+2.40% params), outperforming naive scaling with fewer parameters.
-
1B LLM Pretraining (LLM-1):
- Baseline vs LAUREL-RW+LR (r=4): 0.012% param increase, no measurable latency increase.
- Notable improvements across tasks like GSM8K-CoT (+5.39%), BOOLQ (+13.08%), and BookQA (+20.05%).
-
4B LLM Pretraining (LLM-2):
- LAUREL-RW+LR (r=64): ~0.1% param increase, 1-2% latency increase.
- Improvements on MATH (+4.08%), MGSM (+6.07%), BELEBELE (+8.27%), and multimodal tasks like MMMU (+12.75%).
-
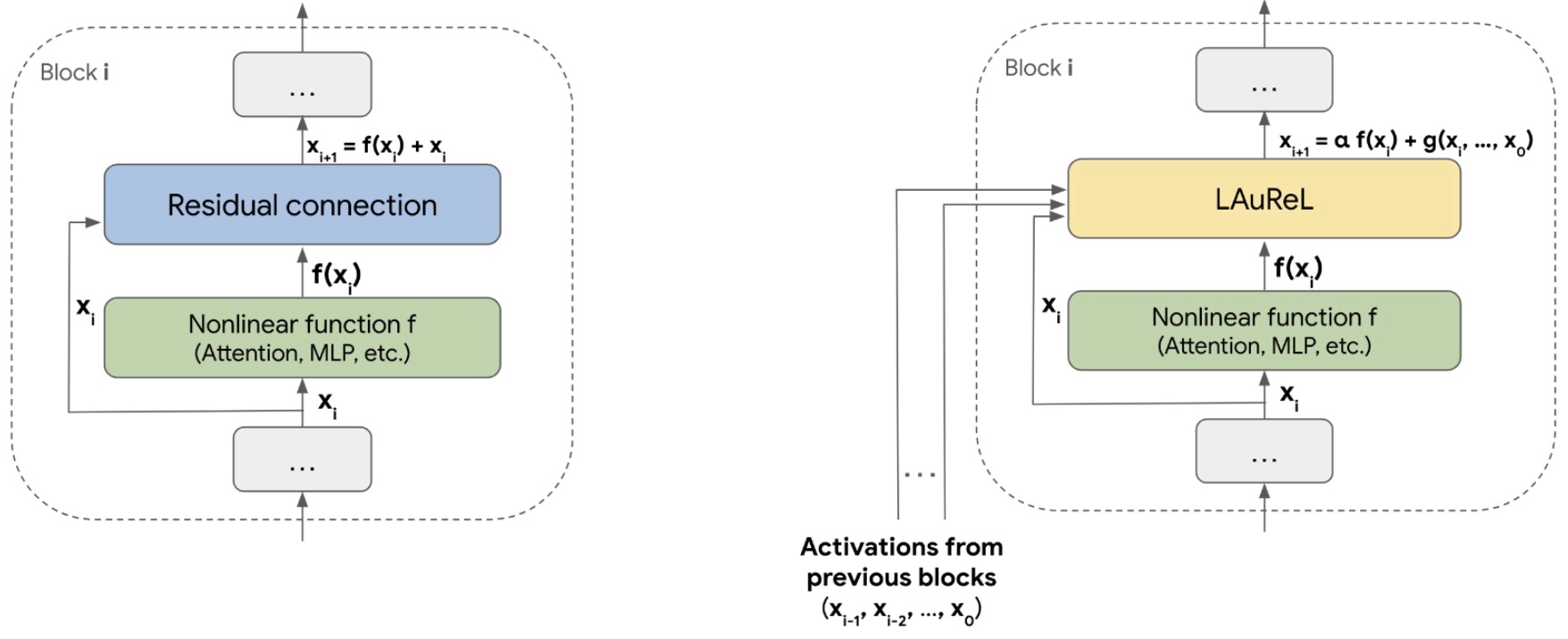
The following figure from the paper shows: (Left) A standard residual connection; the model is divided into logical ‘blocks’, and the residual connection combines the output of a non-linear function \(f\) and the input to this function. (Right) An illustration of the LAUREL framework; LAUREL can be used to replace the regular residual connection. Again, \(f\) can be any non-linear function such as attention, MLPs, and groups of multiple non-linear layers.
-
-
Efficiency and Scalability:
-
LAUREL is designed to be footprint-aware:
- LAUREL-RW: ~constant memory and latency.
- LAUREL-LR: \(\Theta(2rD)\) memory, \(O(rD^2)\) latency.
- LAUREL-PA: \(\Theta(kD)\) memory, \(O(kD)\) latency.
-
LAUREL outperforms naive model scaling both in accuracy and parameter efficiency. For instance, it achieved higher ResNet-50 performance using 2.6× fewer parameters than adding an extra layer.
-
References
-
3D U-Net: learning dense volumetric segmentation from sparse annotation by Çiçek et al. (2016)
-
U-net: Convolutional networks for biomedical image segmentation by Ronneberger et al. (2015)
-
Deep residual learning for image recognition by He et al. (2016).
-
Learning representations by back-propagating errors by Rumelhart et al. (1986)
-
Neural networks and deep learning by Nielsen et al. (2018)
-
Densely connected convolutional networks by Huang (2017)
-
The importance of skip connections in biomedical image segmentation by Drozdzal et al. (2016)
-
Visualizing the loss landscape of neural nets by Li et al. (2018)
Citation
If you found our work useful, please cite it as:
@article{Chadha2020DistilledSkipConnections,
title = {Skip Connections},
author = {Chadha, Aman},
journal = {Distilled AI},
year = {2020},
note = {\url{https://aman.ai}}
}