Primers • Partial Gradient of a Convolutional Layer
Introduction
- The goal of this page is to provide a simple and intuitive explanation of how backprop works for convolutions. Let’s dive in!
Forward Pass
- Let’s start with the forward pass for a single convolutional layer by taking a simple case where number of channels is 1 across all computations.
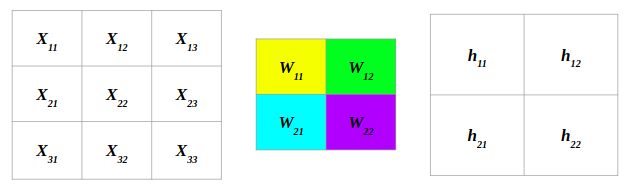
- The following convolution operation takes an input \(X\) of size \(3 \times 3\) using a single filter \(W\) of size \(2 \times 2\) without any padding and \(stride = 1\) generating an output \(H\) of size \(2 \times 2\). Also note that, while performing the forward pass, we will cache the variables \(X\) and filter \(W\). This will help us while performing the backward pass.
- The figure below illustrates the forward pass of the convolution operation:
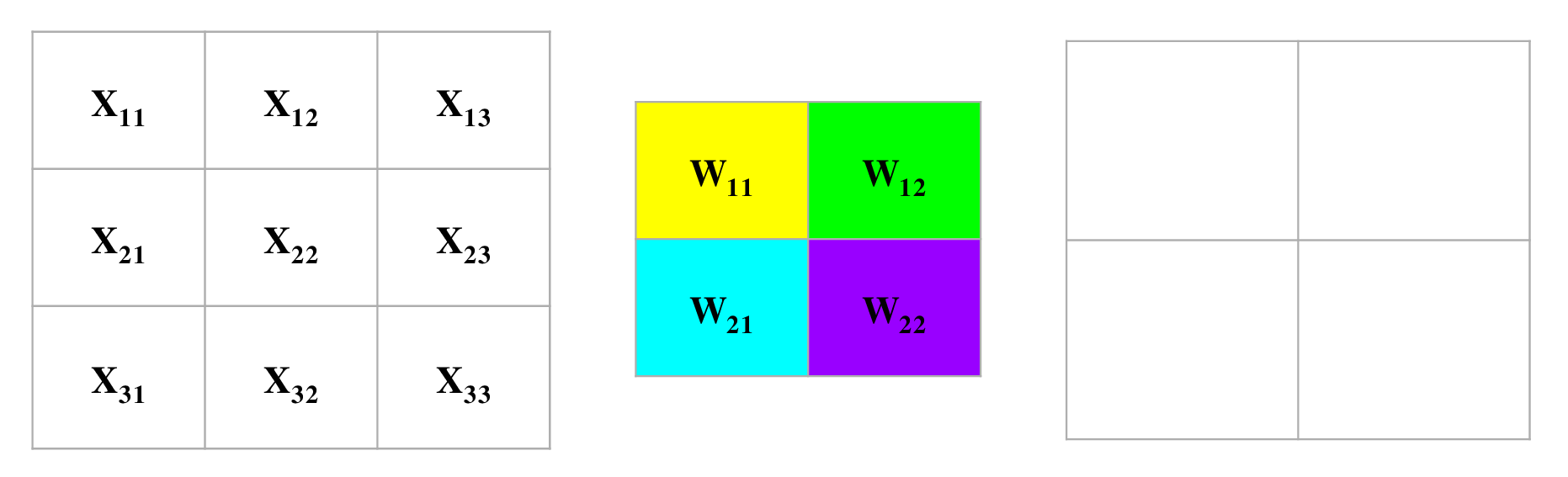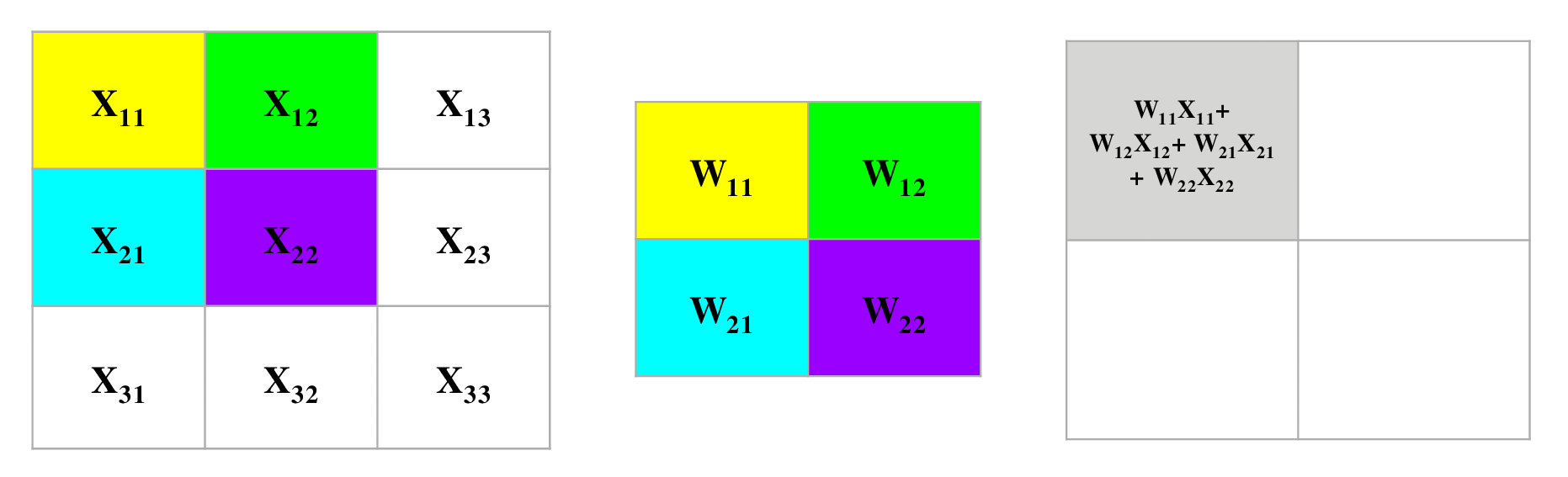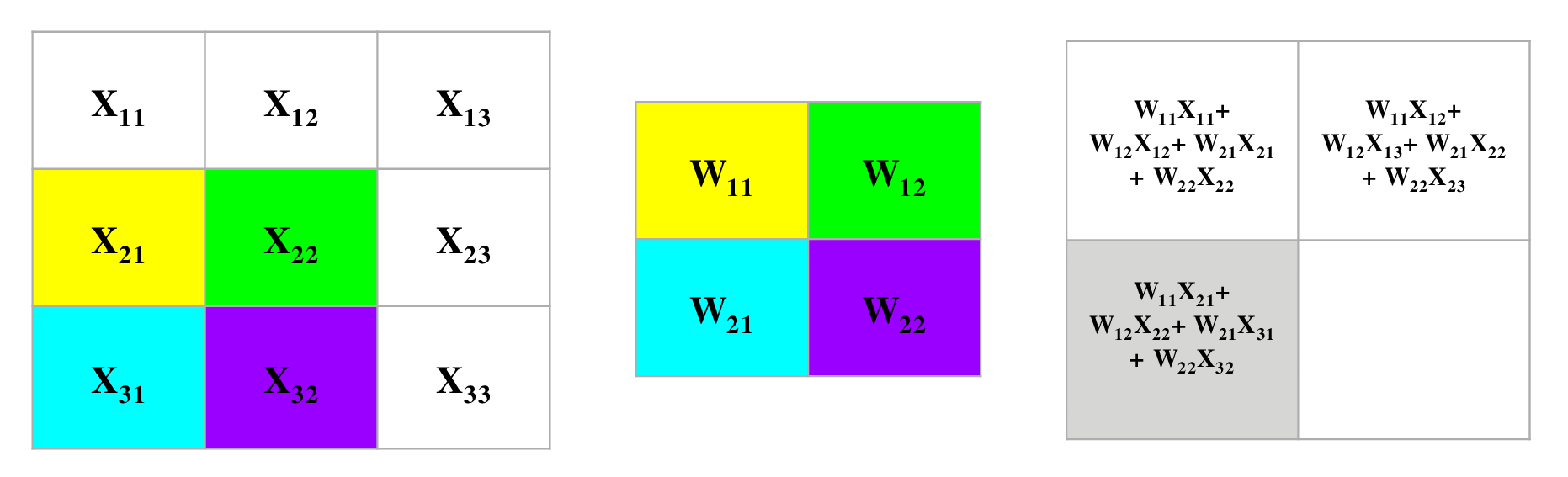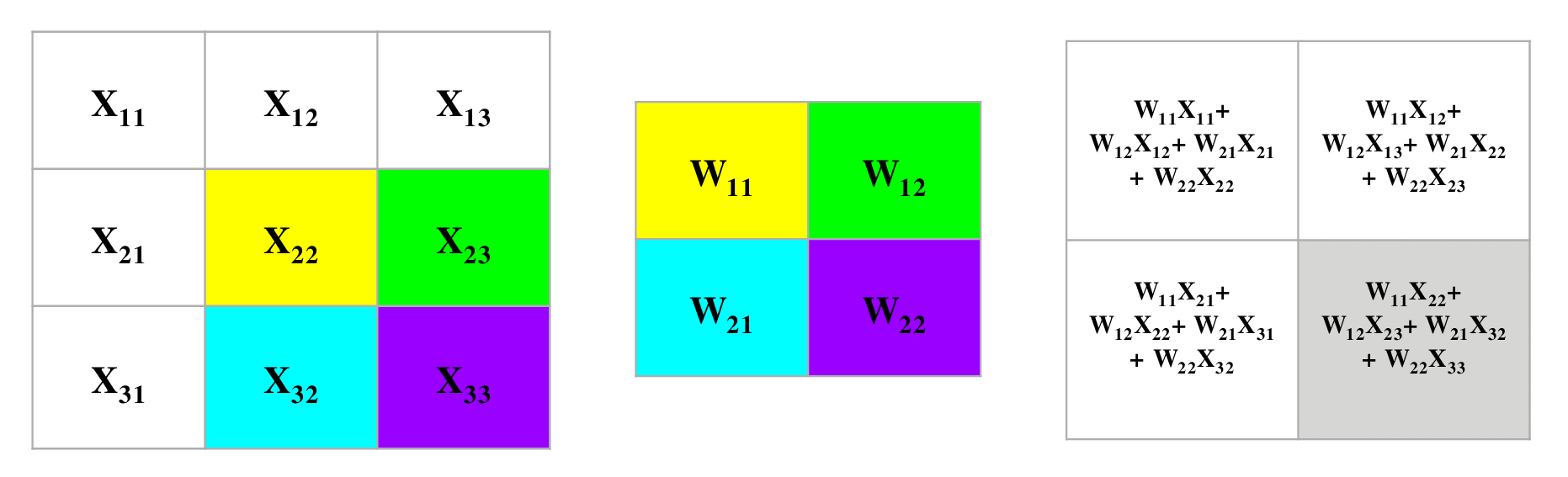
- Note that here we are performing the convolution operation without flipping the filter. This is also referred to as the cross-correlation operation in literature. The above animation is provided just for the sake of clarity. To read more, check out Backpropagation In Convolutional Neural Networks”.
- For an input size of \(3 \times 3\), filter size of \(2 \times 2\) and an output size of \(2 \times 2\):
Backward Pass
- Before moving further, make note of the following notations.
- To implement the back propagation step for the current layer, we can assume that we get \(\partial h\) as input (from the backward pass of the next layer) and our aim is to calculate \(\partial w\) and \(\partial x\). It is important to understand that \(\partial x\) (or \(\partial h\) for the previous layer) would be the input for the backward pass of the previous layer. This is the core principle behind the success of back propagation.
- Each weight in the filter contributes to each pixel in the output map. In other words, any change in a weight in the filter will affect all the output pixels and all these changes add up to contribute to the final loss. Thus, we can easily calculate the derivatives as follows:

- Similarly, we can derive \(\partial x\).
Putting it together with code
Forward and backward pass with a single channel
def conv_forward(X, W):
'''
The forward computation for a convolution function
Arguments:
X -- output activations of the previous layer, numpy array of shape (n_H_prev, n_W_prev) assuming input channels = 1
W -- Weights, numpy array of size (f, f) assuming number of filters = 1
Returns:
H -- conv output, numpy array of size (n_H, n_W)
cache -- cache of values needed for conv_backward() function
'''
# Retrieving dimensions from X's shape
(n_H_prev, n_W_prev) = X.shape
# Retrieving dimensions from W's shape
(f, _) = W.shape
# Compute the output dimensions assuming no padding and stride = 1
n_H = n_H_prev + 1 - f
n_W = n_W_prev + 1 - f
# Initialize the output H with zeros
H = np.zeros((n_H, n_W))
# Looping over vertical(h) and horizontal(w) axis of output volume
for h in range(n_H):
for w in range(n_W):
x_slice = X[h:h+f, w:w+f]
H[h,w] = np.sum(x_slice * W)
# Saving information in 'cache' for backprop
cache = (X, W)
return H, cache
def conv_backward(dH, cache):
'''
The backward computation for a convolution function
Arguments:
dH -- gradient of the cost with respect to output of the conv layer (H), numpy array of shape (n_H, n_W) assuming channels = 1
cache -- cache of values needed for the conv_backward(), output of conv_forward()
Returns:
dX -- gradient of the cost with respect to input of the conv layer (X), numpy array of shape (n_H_prev, n_W_prev) assuming channels = 1
dW -- gradient of the cost with respect to the weights of the conv layer (W), numpy array of shape (f,f) assuming single filter
'''
# Retrieving information from the "cache"
(X, W) = cache
# Retrieving dimensions from X's shape
(n_H_prev, n_W_prev) = X.shape
# Retrieving dimensions from W's shape
(f, _) = W.shape
# Retrieving dimensions from dH's shape
(n_H, n_W) = dH.shape
# Initializing dX, dW with the correct shapes
dX = np.zeros(X.shape)
dW = np.zeros(W.shape)
# Looping over vertical(h) and horizontal(w) axis of the output
for h in range(n_H):
for w in range(n_W):
dX[h:h+f, w:w+f] += W * dH(h,w)
dW += X[h:h+f, w:w+f] * dH(h,w)
return dX, dW
Forward and backward pass with three channels
def conv_forward_naive(x, w, b, conv_param):
"""
A naive implementation of the forward pass for a convolutional layer.
The input consists of N data points, each with C channels, height H and
width W. We convolve each input with F different filters, where each filter
spans all C channels and has height HH and width WW.
Input:
- x: Input data of shape (N, C, H, W)
- w: Filter weights of shape (F, C, HH, WW)
- b: Biases, of shape (F,)
- conv_param: A dictionary with the following keys:
- 'stride': The number of pixels between adjacent receptive fields in the
horizontal and vertical directions.
- 'pad': The number of pixels that will be used to zero-pad the input.
During padding, 'pad' zeros should be placed symmetrically (i.e equally on both sides)
along the height and width axes of the input. Be careful not to modfiy the original
input x directly.
Returns a tuple of:
- out: Output data, of shape (N, F, H', W') where H' and W' are given by
H' = 1 + (H + 2 * pad - HH) / stride
W' = 1 + (W + 2 * pad - WW) / stride
- cache: (x, w, b, conv_param)
"""
# extract params
pad = conv_param['pad']
stride = conv_param['stride']
N, C, H, W = x.shape
F, C, HH, WW = w.shape
# if "(N + 2 * pad - F)/s" does not yield an int, that means our pad/stride
# setting is wrong
assert (H + 2 * pad - HH) % stride == 0, '[Sanity Check] [FAIL]: Conv Layer Failed in Height'
assert (W + 2 * pad - WW) % stride == 0, '[Sanity Check] [FAIL]: Conv Layer Failed in Width'
# output volume size
# note that the // division yields an int (while / yields a float)
Hout = (H + 2 * pad - HH) // stride + 1
Wout = (W + 2 * pad - WW) // stride + 1
# create output volume tensor after convolution
out = np.zeros((N, F, Hout, Wout))
# pad H and W axes of the input data, 0 is the default constant for np.pad
x_pad = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant')
# naive Loops
for n in range(N): # for each neuron
for f in range(F): # for each filter per kernel
for i in range(0, Hout): # for each y activation
for j in range(0, Wout): # for each x activation
# each neuron in a particular depth slide in the output volume
# shares weights over the same HH x WW x C region they're
# looking at in the image; also one bias per filter
out[n, f, i, j] = (x_pad[n, :, i*stride:i*stride+HH, j*stride:j*stride+WW] * w[f, :, :, :]).sum() + b[f]
cache = (x, w, b, conv_param)
return out, cache
def conv_backward_naive(dout, cache):
"""
A naive implementation of the backward pass for a convolutional layer.
Inputs:
- dout: Upstream derivatives.
- cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive
Returns a tuple of:
- dx: Gradient with respect to x
- dw: Gradient with respect to w
- db: Gradient with respect to b
"""
# extract params
x, w, b, conv_param = cache
N, C, H, W = x.shape
F, C, HH, WW = w.shape
stride = conv_param.get('stride', 1)
pad = conv_param.get('pad', 0)
# pad H and W axes of the input data, 0 is the default constant for np.pad
x_pad = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant')
# output volume size
# note that the // division yields an int (while / yields a float)
Hout = (H + 2 * pad - HH) // stride + 1
Wout = (W + 2 * pad - WW) // stride + 1
# construct output
dx_pad = np.zeros_like(x_pad)
dx = np.zeros_like(x)
dw = np.zeros_like(w)
db = np.zeros_like(b)
# naive loops
for n in range(N): # for each neuron
for f in range(F): # for each filter per kernel
db[f] += dout[n, f].sum() # one bias per filter
for i in range(0, Hout): # for each y activation
for j in range(0, Wout): # for each x activation
dw[f] += x_pad[n, :, i * stride:i * stride + HH, j * stride:j * stride + WW] * dout[n, f, i, j]
dx_pad[n, :, i * stride:i * stride + HH, j * stride:j * stride + WW] += w[f] * dout[n, f, i, j]
# extract dx from dx_pad since dx.shape needs to match x.shape
dx = dx_pad[:, :, pad:pad+H, pad:pad+W]
return dx, dw, db
References
- Back Propagation in Convolutional Neural Networks — Intuition and Code
- Derivation of Backpropagation in Convolutional Neural Network (CNN) to delve deeper into mathematics behind gradient calculation for a Conv layer.
- Convolutional Neural Networks backpropagation: from intuition to derivation.
- Backpropagation in Convolutional Neural Networks.
- Convolutional Neural Networks course by deeplearning.ai taught by Andrew Ng on Coursera.
- Back propagation in Convnets lecture by Dhruv Batra at Virginia Tech (now at Georgia Tech) to understand the core concepts behind backprop and how it applies to Conv layers.
- Backpropagation In Convolutional Neural Networks” to learn more about how convolution and cross-correlation relate to each other.
- Stanford’s CS231n lecture on backprop to get an idea of how backpropagation operates on a computational graph.