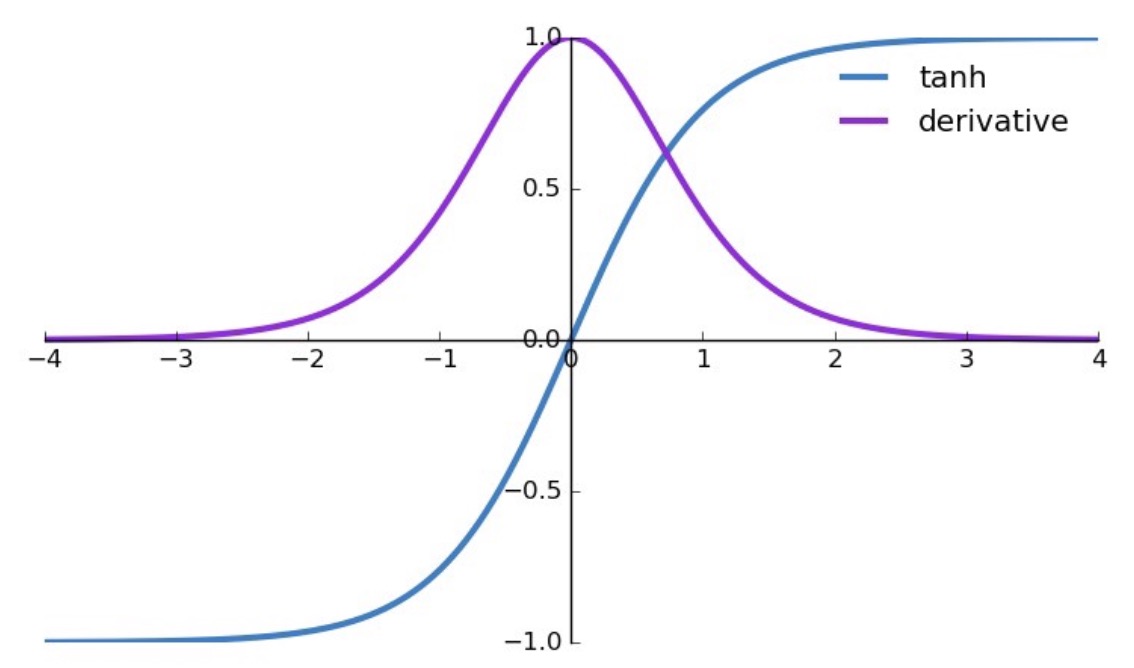
• Prove that the derivative of the tanh function with respect to the input \(z\) is:
\[\frac{d \tanh(z) }{d z}=1-\tanh^{2}(z) =\frac{1}{\cosh^{2}(z) }\]

  • Recall that the tanh function is given by:
\[\tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}\] \[\frac{d(f / g)}{d z}=\frac{g f^{\prime}-f g^{\prime}}{g^{2}}\]
  • Set \(f=\sinh(z) , g=\cosh(z)\) to get:
\[\frac{d \tanh(z) }{d z}=\frac{\cosh(z) \cdot \sinh(z) ^{\prime}-\sinh(z) \cdot \cosh(z) ^{\prime}}{\cosh^{2}(z) }\]
  • Now,
\[\begin{array}{l} \sinh(z) ^{\prime}=\frac{1}{2}\left(e^{z}+e^{-z}\right)=\cosh(z) \\ \cosh(z) ^{\prime}=\frac{1}{2}\left(e^{z}-e^{-z}\right)=\sinh(z) \end{array}\]
  • Thus,
\[\frac{d \tanh(z) }{d z}=\frac{\cosh^{2}(z) -\sinh(z) ^{2}}{\cosh^{2}(z) }=1-\left(\frac{\sinh(z) }{\cosh(z) }\right)^{2}=1-\tanh^{2}(z)\]
  • Now,
\[\frac{1}{\cosh^{2}(z) }=1-\tanh^{2}(z)\]

Proof:

\[1-\frac{\sinh^{2}(z) }{\cosh^{2}(z) }=\frac{\cosh^{2}(z) -\sinh^{2}(z) }{\cosh^{2}(z) }\] \[\operatorname{since}\left(\cosh^{2}(z) \right)-\left(\sinh^{2}(z) \right)=1\] \[\frac{1}{\cosh^{2}(z) }=\operatorname{sech}^{2} z\]

Thus,

\[\boxed{\frac{d \tanh(z) }{d z}=1-\tanh^{2}(z) =\frac{1}{\cosh^{2}(z) }}\]

References