• Prove that the derivative of the Rectified Linear Unit (ReLU) with respect to the input \(z\) is:
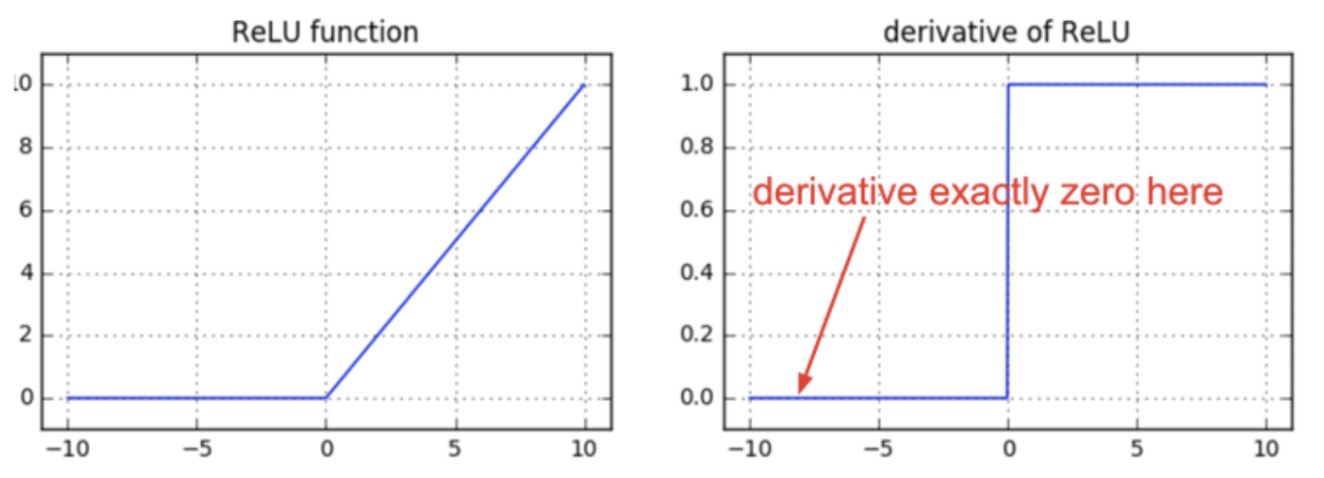
\[\frac{dReLU(z)}{dx}=\left\{\begin{array}{ll} 0 & \text { if z < 0} \\ 1 & \text { if z > 0} \end{array}\right.\]

  • Recall that the RelU performs zero-thresholding of the input, i.e., the input cannot be lower than 0. In other words, it acts as a “gate-keeper” (or a switch) and only propagates forward non-negative inputs, while zeroing out other inputs.
\[ReLU(z)=\left\{\begin{array}{ll} 0 & \text { if z < 0} \\ z & \text { if z > 0} \end{array}\right.\]
  • Put simply,
\[ReLU(z) = max(0,z)\]

  • So the output of a ReLU is either \(z\) or 0, depending on whether the input is non-negative or negative respectively. Note that the ReLU is not defined at 0, so there must be a convention to set it either at 0 or 1 in this case.

  • As such, the derivative of ReLU with respect to the input \(z\) is:

\[\boxed{\frac{dReLU(z)}{dz}=\left\{\begin{array}{ll} 0 & \text { if z < 0} \\ 1 & \text { if z > 0} \end{array}\right.}\]
  • Intuitively, the derivative of the ReLU indicates that the error either fully propagates to the previous layer (owing to the 1) in case if the input to the ReLU is non-negative, or is completely stopped (owing to the 0) if the input to ReLU is negative.