Natural Language Processing • xLSTM
Overview
-
The exploration of Long Short-Term Memory (LSTM) networks has led to significant advancements in our understanding of sequence learning and memory mechanisms in neural models. Originating in the early 1990s, LSTMs were designed to combat the vanishing gradient problem prevalent in traditional recurrent neural networks, enabling models to remember information over longer periods. This was achieved through the introduction of a gating mechanism that regulates the flow of information, consisting of three gates: the input, forget, and output gates. These structures allow the network to selectively remember and forget information, a crucial ability for tasks involving long or complex temporal sequences.
-
Despite their success, LSTMs have faced challenges, particularly when compared to newer architectures like the Transformer. Introduced in 2017, Transformers utilize self-attention mechanisms that allow for more parallelizable operations and have shown greater efficacy at scale, particularly in tasks like machine translation and large-scale language models. This shift has raised questions about the potential and scalability of LSTMs in the era dominated by Transformer models.
-
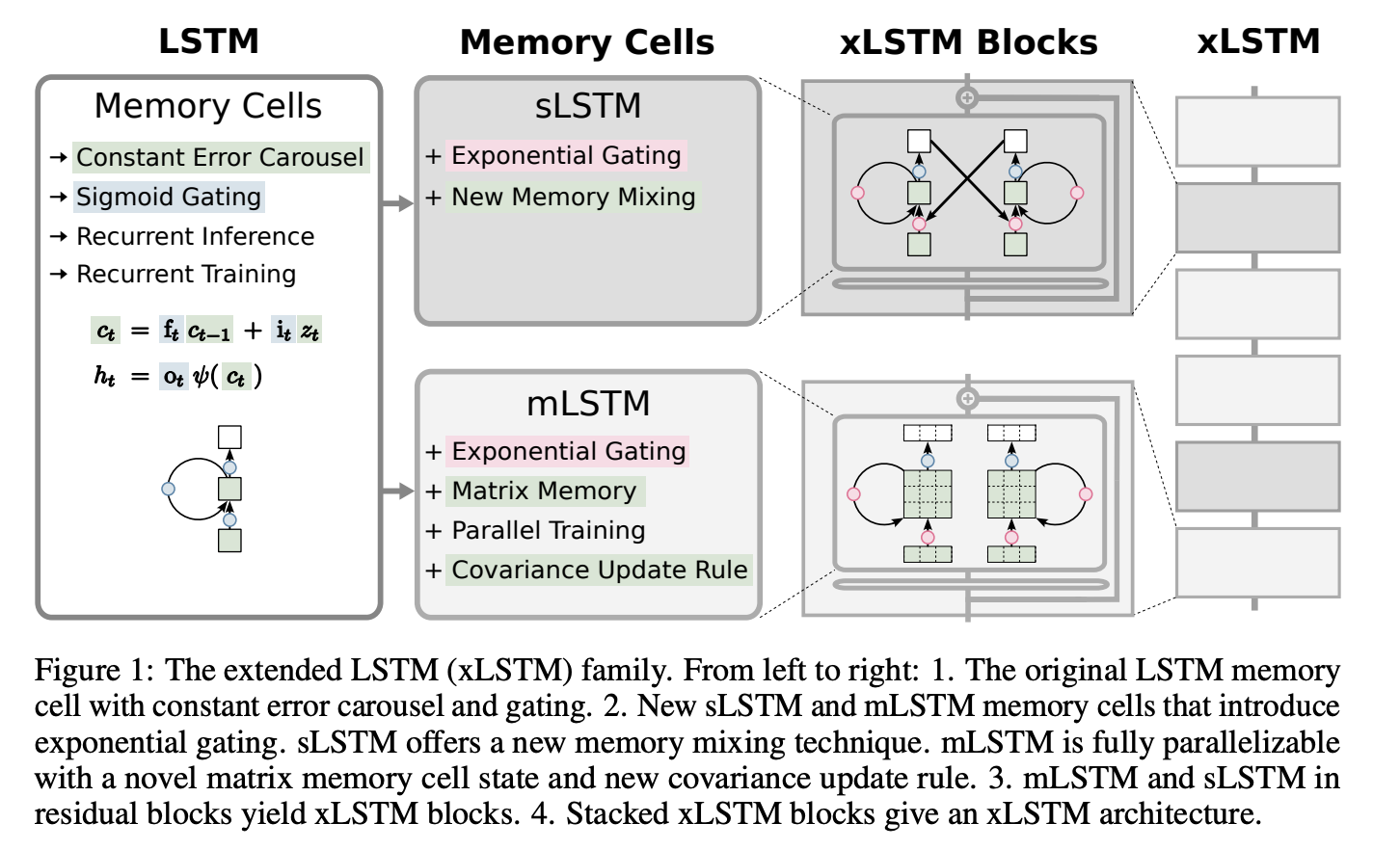
The development of Extended Long Short-Term Memory (xLSTM) represents an innovative leap to revitalize LSTM architectures by addressing their limitations. By integrating advancements such as exponential gating and novel memory structures—scalar and matrix memories—xLSTMs aim to enhance the traditional LSTM’s capability to handle larger and more complex datasets effectively. This evolution not only maintains the LSTM’s ability to manage sequential data with high temporal resolution but also promises to improve performance and scalability, potentially rivaling that of Transformer-based models.
The Extended Long Short-Term Memory (xLSTM) architecture enhances the traditional LSTM framework to address its inherent limitations, particularly in scalability and memory efficiency. The key innovations in xLSTM include exponential gating and advanced memory structures, which are designed to refine how the model processes and retains information over time.
In the xLSTM model described in the paper you mentioned, two significant enhancements to the traditional Long Short-Term Memory (LSTM) architecture are introduced: Exponential Gating and Parallelizable Matrix Memory. Here’s an explanation of each:
Exponential Gating
- Exponential gating is a modification to the traditional gating mechanisms found in standard LSTMs, which typically use sigmoid functions to control the flow of information through the network. These sigmoid gates help the model decide how much of the past information to forget and how much of the new information to incorporate into the cell state.
- In contrast, exponential gating uses exponential functions to manage these decisions. The primary advantage of using exponential functions over sigmoid functions is that they can offer a more dynamic range of update values, potentially responding more sensitively to different input conditions. This can be particularly useful in tasks where the importance of information varies dramatically over time, allowing the model to adapt its memory content more aggressively or conservatively depending on the context.
- This change aims to help the network better capture long-term dependencies and nuances in data by providing a richer and more flexible mechanism to update its internal state, which is crucial for complex sequence modeling tasks.
- Traditional LSTMs utilize sigmoid functions for their gates, which control the flow of information by selectively adding or removing content from the cell state. In xLSTM, exponential gating replaces the traditional sigmoid functions, allowing the gates to control the flow of information more dynamically. This is crucial for tasks where the importance of information varies significantly over different parts of the sequence. Exponential gating helps in adjusting the network’s sensitivity and responsiveness, potentially leading to better handling of long-range dependencies within data.
Parallelizable Matrix Memory
- Parallelizable Matrix Memory extends the concept of the LSTM’s memory cell to support matrix-based, rather than vector-based, representations. This innovation is significant because it allows the LSTM to handle more information simultaneously and supports more complex data interactions within the memory cell itself.
- In traditional LSTMs, the memory cell is updated using vector operations, which inherently limits the complexity and richness of the relationships the model can learn. By extending this to matrices, the xLSTM can encode a richer set of features and interactions at each time step. This matrix memory is updated through a covariance update rule, which effectively captures the outer product of vectors, thus allowing the model to learn higher-order interactions between features.
- Moreover, this matrix-based approach can be fully parallelized. In standard LSTMs, the recurrent nature of the computation—where each step depends on the previous step—makes true parallelization challenging. However, with matrix memory, many of the operations can be computed in parallel, significantly speeding up the processing time. This is particularly advantageous when deploying models in environments where execution speed is critical, such as real-time applications or when processing exceptionally large datasets.
Advanced Memory Structures
-
xLSTM introduces two significant modifications in memory structures: scalar and matrix memories. The scalar memory (sLSTM) and matrix memory (mLSTM) enhancements allow for different methods of data retention:
-
Scalar Memory (sLSTM): This modification simplifies the memory cell to operate with scalar values but introduces a novel way of mixing memories, which enhances the model’s ability to update and manipulate its internal state based on incoming information.
-
Matrix Memory (mLSTM): This approach expands the memory cell to store information in a matrix form, allowing the network to capture not just the sequence but also the relationships between different features within the data. This is particularly useful for complex tasks such as image captioning or multi-faceted decision-making processes where relationships between inputs significantly influence the output.
Integration into Residual Networks
-
Both sLSTM and mLSTM can be integrated into residual network architectures. This integration allows for the stacking of multiple xLSTM blocks, enhancing the model’s depth and complexity without the risk of vanishing gradients, a common problem in deep neural networks. The use of residual connections helps in stabilizing the learning process and enables the model to learn from both recent and long-past inputs effectively.
-
The combination of these enhancements aims to position xLSTM as a robust alternative to Transformer models, especially in scenarios where temporal dynamics are critical. By improving the gating mechanisms and memory structures, xLSTM is designed to handle larger datasets more efficiently, potentially leading to better performance in a wide range of sequence learning tasks.
Overall impact
- Together, exponential gating and parallelizable matrix memory make xLSTM a powerful architecture, especially for applications involving complex, long-term sequential data. By enhancing the gating mechanisms and memory structure, xLSTM not only improves on the foundational strengths of traditional LSTMs but also addresses some of their well-known limitations, such as difficulty with very long sequences and parallelizability. These advancements position xLSTM as a robust alternative to other state-of-the-art models like Transformers, particularly in scenarios where efficient processing of long sequences is crucial.
Results
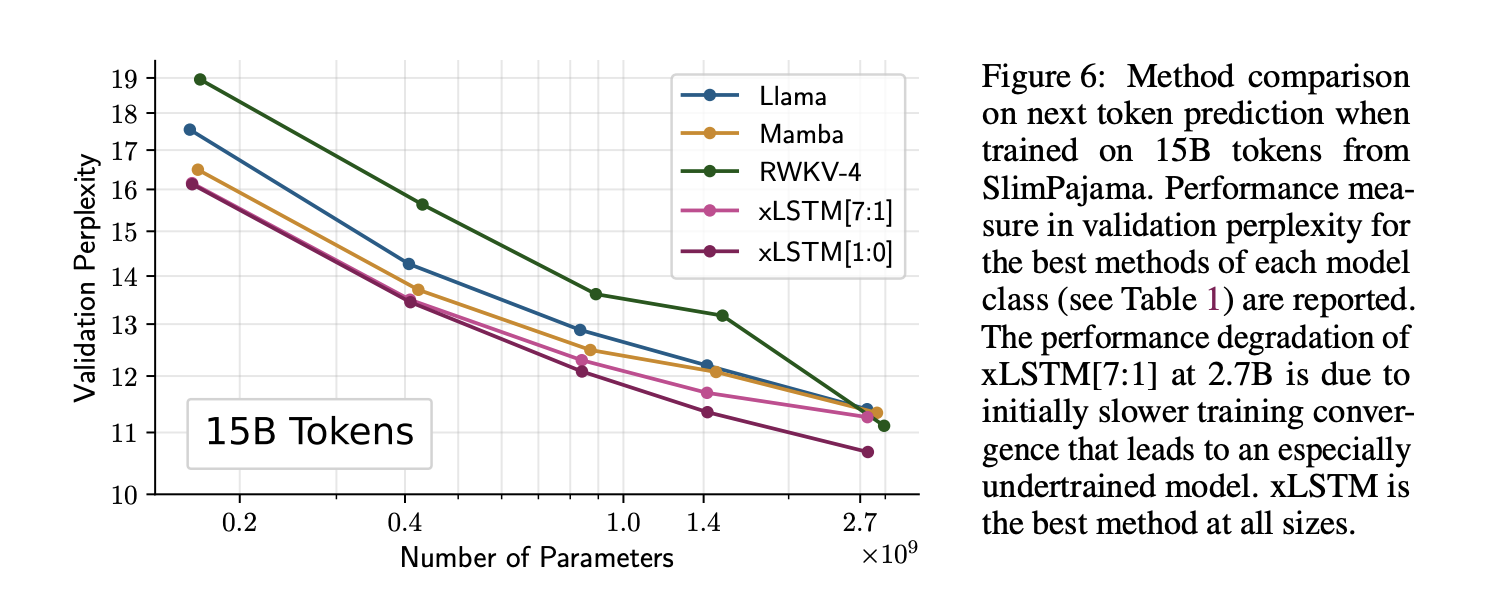
- This graph displays a comparison of different machine learning models based on their performance in next token prediction tasks. The models have been trained on a dataset comprising 15 billion tokens from SlimPajama. The key metric used to measure performance is validation perplexity, which quantifies how well a probabilistic model predicts a sample. A lower perplexity indicates better predictive performance.
- xLSTM models, especially the xLSTM[1:0], generally outperform the other models across the board in terms of validation perplexity, making it the most effective model in this comparison.
- The performance of xLSTM[7:1] highlights a potential issue with scaling at very high parameter counts (2.7 billion), suggesting that while xLSTM models are effective, their training dynamics might vary significantly with size and require careful tuning to avoid performance degradation.
-
The general trend shows that increasing the number of parameters tends to improve the performance of all models, highlighting the importance of model capacity in handling large-scale language modeling tasks.
- xLSTM is O(N) time complexity and O(1) memory complexity as the length of sequence increases. Transformer time AND memory complexity is quadratic O(N^2), so comparatively xLSTM is much better.