Primers • SVM Kernel/Polynomial Trick
Kernel/Polynomial Trick
-
In classic mathematical induction, the goal of a classification task is to learn a function \(y = f(x; \theta)\) aka fit a model (or a curve) to the data with a decision boundary that separates the classes (say, approve/reject loan applications).
-
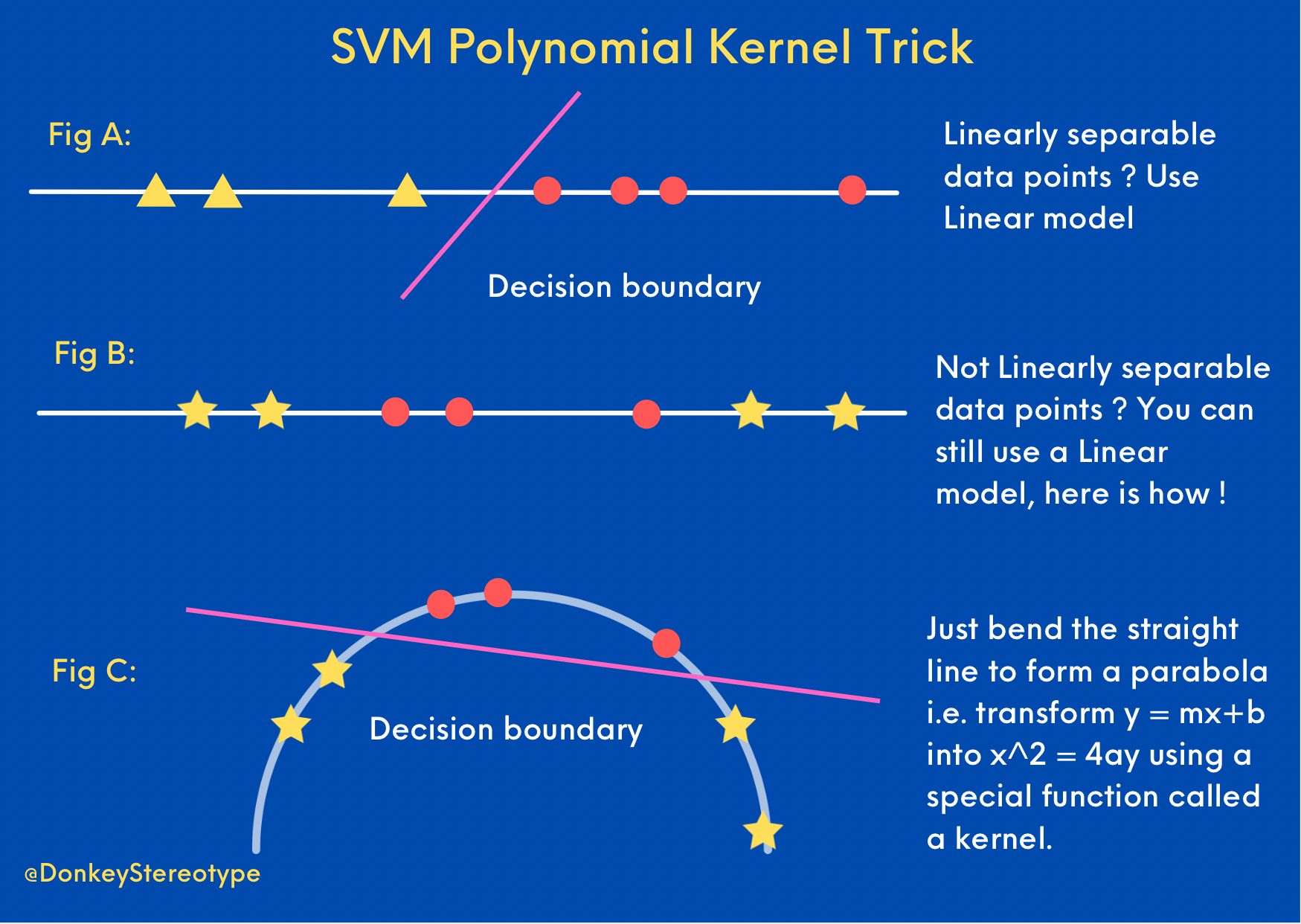
The diagram below from Prithvi Da summarizes the approaches.
-
Fig A: If the data points are linearly separable, it’s simple you can fit a linear model using algorithms like Logistic regression or SVM.
-
Fig B: What do you do if the data points are NOT linearly separable? of course we can fit a Neural network which in theory can learn any Borel measurable function under the sky. But we have a simple solution especially if you have a smaller tabular dataset.
-
Fig C: Shows you can simply magically transform a line to a parabola and then learn a function that linearly separates the data points. This idea of applying a non-linear transformation using a special function called a “kernel” to convert linear input space (\(y= mx+c\), 1st-degree polynomial) to a high degree polynomial (\(x^2 = 4ay\), 2nd-degree polynomial) is the gist of the kernel trick. The bottom-line is that learning a linear model in the higher-dimensional space is equivalent to learning a non-linear model in the original lower-dimensional input space.
-
TL;DR - It pays in spades to bend the problem, literally sometimes.
References
Citation
If you found our work useful, please cite it as:
@article{Chadha2020DistilledKernelTrick,
title = {Kernel Trick},
author = {Chadha, Aman},
journal = {Distilled AI},
year = {2020},
note = {\url{https://aman.ai}}
}