Background

  • State Space Models (SSMs) are a class of mathematical models used in various fields for describing systems that evolve over time. These models are characterized by their ability to represent dynamic systems through state variables and equations that capture the relationships between these variables.
  • This primer offers an overview of State Space Models and their application in deep learning.

Motivation

  • Some of the common themes in the search for new architectures that do not have the drawbacks that the Transformer architectures suffers from (quadratic time and space complexity, large parameter count, etc.) are based on designing a mathematical framework/system for mapping the input sequence to an output sequence, such that:
    1. Allows for processing sequences in parallel during training.
    2. Being able to express the output as a recurrence equation during inference time. Constant state size further boosts inference time speed and memory requirements thanks to the fact that we no longer need a linearly growing KV cache.
    3. Framing the input sequence to output sequence mapping through mathematical models such as State Space Models allows for 1 and 2.
    4. Leveraging Fast Fourier Transformations to perform convolutional operations. Convolutional operations in the frequency domain can be implemented as pointwise multiplications. Hyena Hierarchy and StripedHyena are two examples that leverage this observation.

State Space Models: Overview

  1. Definition: A State Space Model typically consists of two sets of equations:
    • State Equations: These describe how the state of the system evolves over time.
    • Observation Equations: These link the state of the system to the measurements or observations that are made.
  2. Components:
    • State Variables: Represent the system’s internal state at a given time.
    • Inputs/Controls: External inputs that affect the state.
    • Outputs/Observations: What is measured or observed from the system.
  3. Usage: SSMs are widely used in control theory, econometrics, signal processing, and other areas where it’s crucial to model dynamic behavior over time.

SSMs in Deep Learning

  1. Combination with Neural Networks:
    • SSMs can be combined with neural networks to create powerful hybrid models. The neural network component can learn complex, nonlinear relationships in the data, which are then modeled dynamically through the state space framework.
    • This is particularly useful in scenarios where you have time-series data or need to model sequential dependencies.
  2. Time Series Analysis and Forecasting:
    • In deep learning, SSMs are often applied to time series analysis and forecasting. They can effectively capture temporal dynamics and dependencies, which are crucial in predicting future values based on past and present data.
    • Recurrent neural networks (RNNs) and Long Short-Term Memory (LSTM) networks are examples of deep learning models that can be viewed as a form of state space model.
  3. Reinforcement Learning:
    • In reinforcement learning, SSMs can be used to model the environment in which an agent operates. The state space represents the state of the environment, and the agent’s actions influence the transition between states.
    • This is particularly relevant in scenarios where the environment is partially observable or the dynamics are complex.
  4. Data Imputation and Anomaly Detection:
    • SSMs in deep learning can be applied to tasks like data imputation (filling in missing data) and anomaly detection in time-series data. They are capable of understanding normal patterns and detecting deviations.
  5. Customization and Flexibility:
    • Deep learning allows for the customization of the standard state space model structure, enabling the handling of more complex and high-dimensional data, which is common in modern applications.

Theory of SSMs

Conclusion

  • The integration of State Space Models with deep learning represents a powerful approach to modeling dynamic systems, especially in scenarios involving time-series data or environments with temporal dependencies. The flexibility and adaptability of these models make them suitable for a wide range of applications, from forecasting and anomaly detection to complex reinforcement learning environments.

FAQ

How do SSMs compare with Transformers in terms of time complexity?

  • Transformers and state-space models (SSMs) differ significantly in their computational complexity, particularly in how they handle sequence lengths during inference.

Transformers

  • Quadratic Time Inference: Transformers offer quadratic time inference due to the self-attention mechanism. In the self-attention layer, every token in the input sequence attends to every other token. This operation requires computing a similarity score (dot product) between each pair of tokens, resulting in a \(O(n^2)\) complexity, where \(n\) is the sequence length. Specifically:

    1. Attention Mechanism: For an input sequence of length \(n\), the self-attention mechanism involves calculating attention scores for each pair of tokens, which is an \(n \times n\) operation.
    2. Softmax and Weighted Sum: After computing the attention scores, applying the softmax function and then performing a weighted sum to obtain the final attention outputs also maintains \(O(n^2)\) complexity.

  • Thus, the self-attention component of Transformers results in quadratic time complexity with respect to the sequence length.

State-Space Models (SSMs)

  • Linear Time Inference: State-space models (SSMs) achieve linear time inference through a fundamentally different approach. SSMs model the sequence data using a state-space representation, which allows them to process sequences in a more efficient manner.

    1. State-Space Representation: SSMs use state variables to represent the underlying system. These state variables evolve over time according to a state transition equation. For a sequence of length \(n\), the state transitions can be computed in \(O(n)\) time.
    2. Convolutional Operations: Many implementations of SSMs use convolutional operations to handle the sequence data. Convolutions can be computed efficiently using Fast Fourier Transform (FFT) techniques, which can reduce the complexity of applying the convolution to \(O(n \log n)\), but for many practical purposes, the complexity is often approximated to be closer to \(O(n)\).

  • In summary:

    • Transformers have quadratic time complexity \(O(n^2)\) due to the self-attention mechanism, where \(n\) is the sequence length.
    • SSMs achieve linear time complexity \(O(n)\) by leveraging state-space representations and efficient convolutional operations, allowing them to handle long sequences more efficiently than Transformers.

  • These differences make SSMs particularly attractive for tasks requiring efficient processing of long sequences, while Transformers remain popular for their flexibility and effectiveness across a wide range of tasks despite their higher computational complexity for long sequences.

Models

Jamba

  • Jamba is AI21’s Groundbreaking SSM-Transformer Model, which represents a novel leap in language model architecture by integrating Mamba Structured State Space (SSM) technology with the traditional Transformer model, creating the world’s first production-grade Mamba based model. This hybrid approach notably addresses the scalability and performance limitations of pure SSM or Transformer models, providing a substantial increase in efficiency and throughput. Key advancements include a 256K context window and the capacity to fit up to 140K context on a single GPU, marking it as a leader in its class.
  • To capture the best that both Mamba and Transformer architectures have to offer, we developed the corresponding Joint Attention and Mamba (Jamba) architecture. Composed of Transformer, Mamba, and mixture-of-experts (MoE) layers, Jamba optimizes for memory, throughput, and performance – all at once – as depicted in the table below.

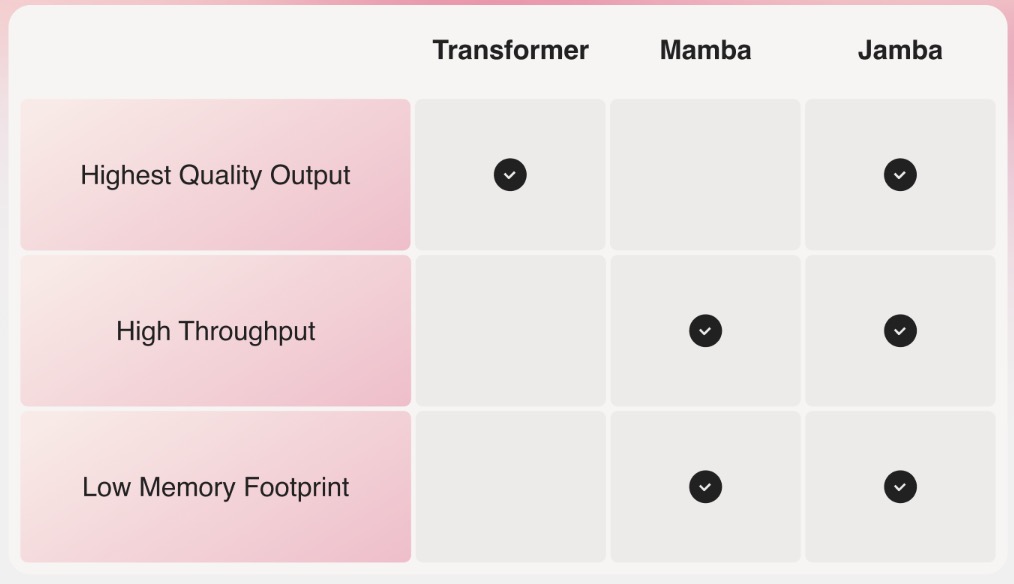
  • The architecture of Jamba combines Transformer layers, Mamba layers, and mixture-of-experts (MoE) layers to optimize memory usage, computational throughput, and overall performance. One of the critical innovations is the use of MoE layers, allowing Jamba to selectively utilize just 12B out of its available 52B parameters during inference, making it significantly more efficient than a Transformer model of equivalent size.
  • As depicted in the diagram below, AI21’s Jamba architecture features a blocks-and-layers approach that allows Jamba to successfully integrate the two architectures. Each Jamba block contains either an attention or a Mamba layer, followed by a multi-layer perceptron (MLP), producing an overall ratio of one Transformer layer out of every eight total layers.

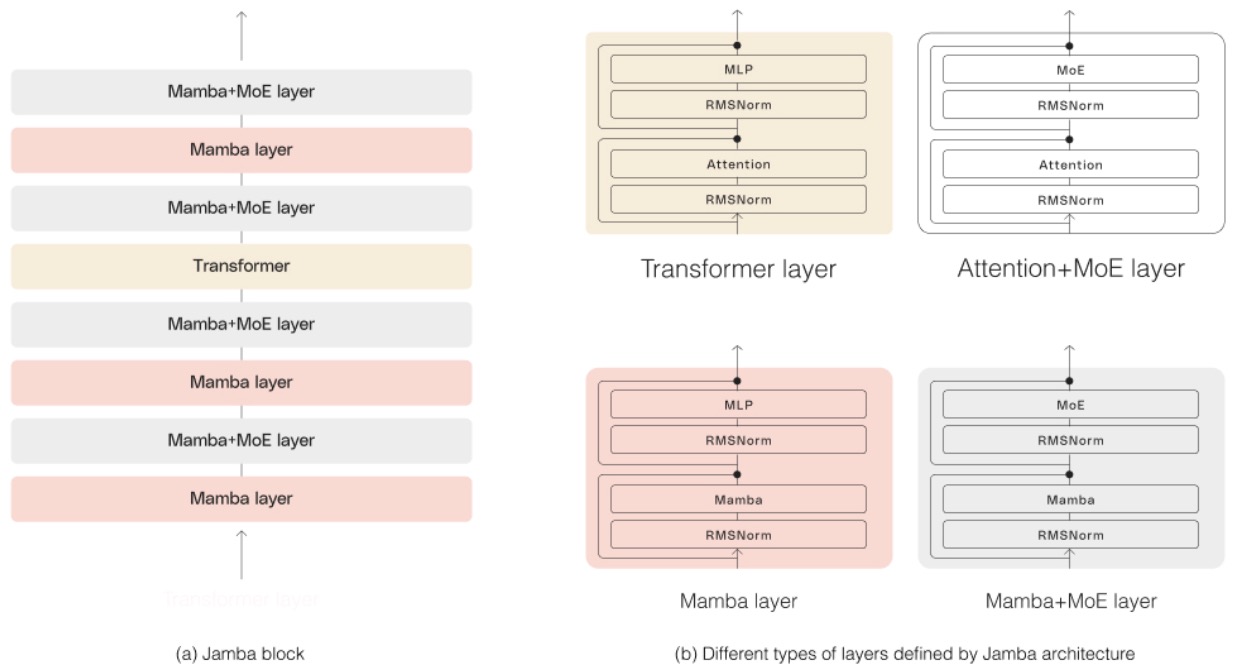
  • Jamba has been scaled to a production-grade level, a feat previously unachieved by Mamba models beyond 3B parameters. Its architecture employs a blocks-and-layers design that alternates between attention or Mamba layers and multi-layer perceptrons (MLP), with a Transformer layer included for every eight total layers. This design is instrumental in optimizing the model for high-quality output and throughput on common hardware, such as a single 80GB GPU.
  • Significant results have been observed in Jamba’s performance, with a 3x improvement in throughput on long contexts compared to similar models like Mixtral 8x7B, without compromising on efficiency. These achievements have been made possible by innovative engineering choices, including the strategic use of MoE layers to manage computational demands and the integration of Mamba with Transformer architectures for superior model capacity and efficiency.
  • Jamba is released with open weights under Apache 2.0, encouraging further exploration and development within the AI community. Additionally, it’s made accessible via Hugging Face and is slated for inclusion in the NVIDIA API catalog, facilitating its adoption in enterprise applications through the NVIDIA AI Enterprise software platform.

Efficiently Modeling Long Sequences with Structured State Spaces

  • The paper, authored by Gu et al. from Stanford University, introduces a new sequence model named Structured State Space Sequence model (S4), designed to efficiently handle long-range dependencies (LRDs) in data sequences extending over 10,000 steps or more.
  • S4 leverages a novel parameterization of the state space model (SSM), enabling it to efficiently compute tasks while maintaining high performance traditionally achieved by models like RNNs, CNNs, and Transformers. Specifically, it uses a reparameterization of the structured state matrices in SSMs by combining a low-rank correction with a normal term, allowing for efficient computations via the Cauchy kernel, reducing the operational complexity to \(O(N+L)\) for state size \(N\) and sequence length \(L\).
  • The model significantly outperforms existing models on the Long Range Arena benchmark, addressing tasks previously infeasible due to computational constraints. For example, it achieves 91% accuracy on sequential CIFAR-10 and solves the challenging Path-X task (16k length) with 88% accuracy, a task where other models performed no better than random.
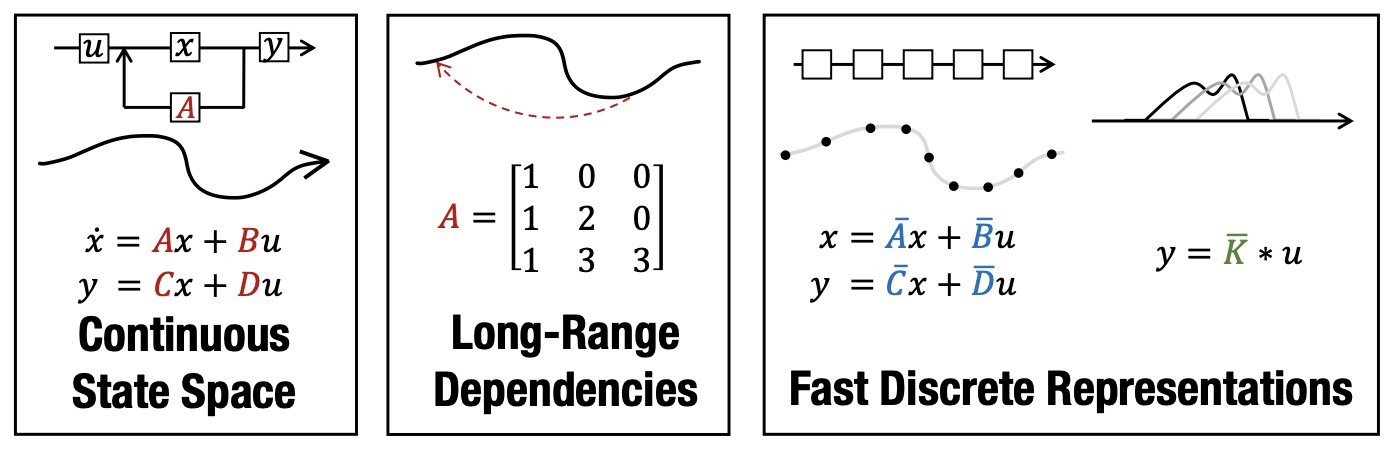
  • The figure below from the paper shows: (Left) State Space Models (SSM) parameterized by matrices \(A\), \(B\), \(C\), \(D\) map an input signal \(u(t)\) to output \(y(t)\) through a latent state \(x(t)\). (Center) Recent theory on continuous-time memorization derives special A matrices that allow SSMs to capture LRDs mathematically and empirically. (Right) SSMs can be computed either as a recurrence (left) or convolution (right). However, materializing these conceptual views requires utilizing different representations of its parameters (red, blue, green) which are very expensive to compute. S4 introduces a novel parameterization that efficiently swaps between these representations, allowing it to handle a wide range of tasks, be efficient at both training and inference, and excel at long sequences.

  • Implementation details include the use of the HiPPO framework to derive specific matrices that help capture long-range dependencies more effectively. S4 transitions between continuous-time, recurrent, and convolutional representations of the SSM, which accommodates various data modalities and sequence lengths efficiently.
  • Additionally, the paper discusses the architecture of the S4 layer in depth, detailing how it uses the state space to model sequences across different domains, such as images, audio, and text, with minimal domain-specific tailoring. It also explains how S4 handles changes in time-series sampling frequency without retraining, an important feature for real-world applications.

Mamba: Linear-Time Sequence Modeling with Selective State Spaces

  • This paper by Gu and Dao from presents ‘Mamba’, a neural network architecture for sequence modeling. Mamba addresses the computational inefficiencies of Transformers in processing long sequences, a significant issue in modern deep learning, particularly with foundation models.
  • They propose selective state space models (SSMs) that enable linear scaling with sequence length and demonstrate superior performance across different modalities including language, audio, and genomics.
  • The authors highlight that traditional SSMs struggle with discrete and information-dense data like text due to their inability for content-based reasoning. By making SSM parameters input-dependent, Mamba can selectively process information, improving its adaptability and performance. This innovative approach allows selective information retention across sequences, crucial for coherent text generation and understanding.
  • To maintain computational efficiency despite the loss of efficient convolution operations due to input-dependent parameters, the authors develop a hardware-aware parallel algorithm for SSM computation. This innovation avoids extensive memory access and leverages GPU memory hierarchy effectively, leading to significant speedups. The architecture integrates these selective SSMs into a single block, eliminating the need for attention or MLP blocks, resulting in a homogeneous and efficient design.
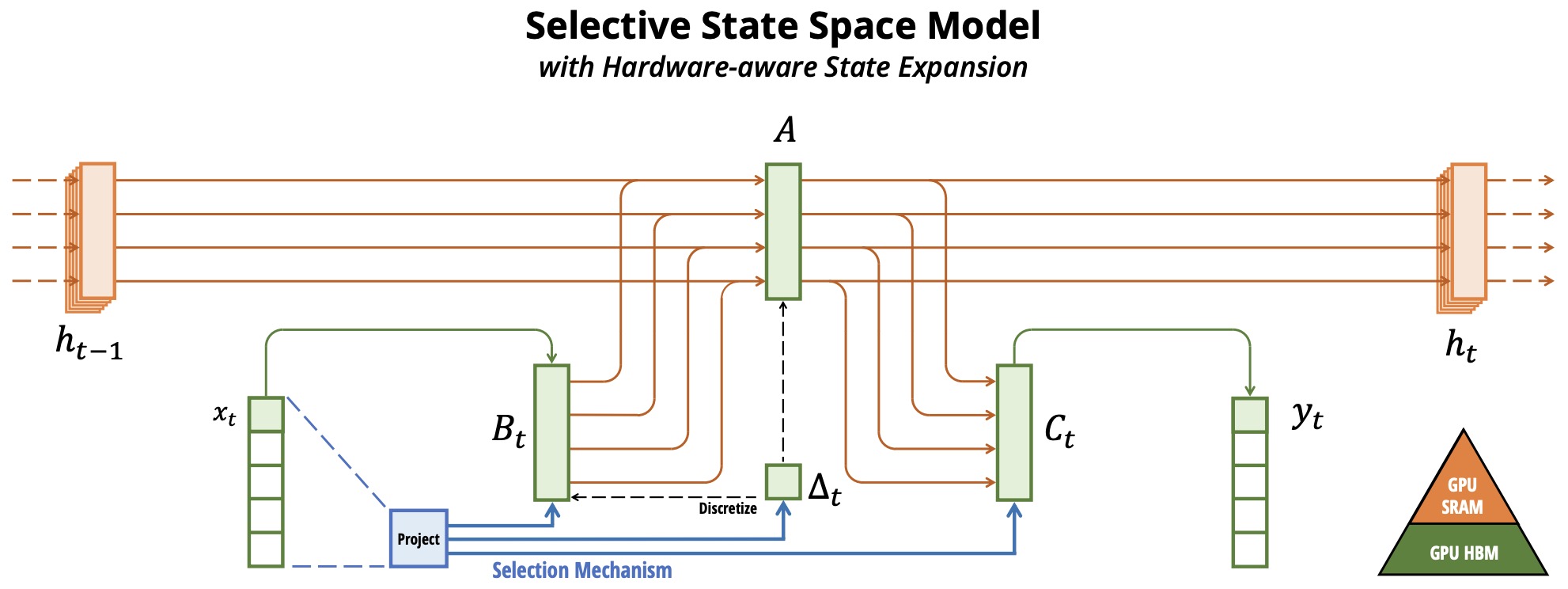
  • Mamba’s architecture simplifies previous deep sequence models by integrating selective SSMs without the need for attention or MLP blocks, achieving a homogeneous and simplified design. This results in a model that not only performs well on tasks requiring long-range dependencies but also offers rapid inference. The following figure from the paper shows: (Overview.) Structured SSMs independently map each channel (e.g., \(D\) = 5) of an input \(x\) to output \(y\) through a higher dimensional latent state \(h\) (e.g., \(N\) = 4). Prior SSMs avoid materializing this large effective state (\(DN\), times batch size \(B\) and sequence length \(L\)) through clever alternate computation paths requiring time-invariance: the \((\Delta, A, B, C)\) parameters are constant across time. Mamba’s selection mechanism adds back input-dependent dynamics, which also requires a careful hardware-aware algorithm to only materialize the expanded states in more efficient levels of the GPU memory hierarchy.

  • In empirical evaluations, Mamba sets new performance benchmarks in tasks such as selective copying and induction heads, showcasing its ability to solve problems that challenge other models. In language modeling, Mamba outperforms Transformers of similar or even larger sizes, offering better scaling laws and downstream task performance. Additionally, in DNA modeling and audio generation, Mamba achieves state-of-the-art results, benefiting from its ability to process long sequences efficiently.
  • Mamba demonstrates superior performance in various tasks like language, audio, and genomics. It outperforms Transformers of the same size in language modeling and achieves five times higher throughput, scaling linearly in sequence length. Its versatility is showcased through empirical validation on tasks such as synthetic copying, induction heads, language modeling, DNA modeling, and audio modeling and generation. The model’s significant speed improvements and scalability could redefine efficiency standards in foundation models across different modalities.
  • The paper also discusses the significance of the selection mechanism in SSMs, connecting it to gating mechanisms in recurrent neural networks and highlighting its role in modeling variable spacing and context in sequences. This mechanism allows Mamba to focus on relevant information and ignore noise, which is crucial for handling long sequences in various domains.
  • Model ablations and comparisons demonstrate the critical components contributing to Mamba’s performance, including the impact of selective parameters and the architecture’s simplified design. The authors release the model code and pre-trained checkpoints, facilitating further research and application in the field.

MambaByte: Token-free Selective State Space Model

  • This paper by Wang et al. from Cornell introduced MambaByte, a novel adaptation of the Mamba state space model designed for efficient language modeling directly from raw byte sequences. Addressing the challenges posed by the significantly longer sequences of bytes compared to traditional subword units, MambaByte leverages the computational efficiency of state space models (SSMs) to outperform existing byte-level models and rival state-of-the-art subword Transformers.
  • MambaByte’s architecture is distinguished by its selective mechanism tailored for discrete data like text, enabling linear scaling in length and promising faster inference speeds compared to conventional Transformers. This breakthrough is attributed to the model’s ability to efficiently process the extended sequences inherent to byte-level processing, eliminating the need for subword tokenization and its associated biases.
  • The figure below from the paper shows a Mamba block. \(\sigma\) indicates Swish activation.

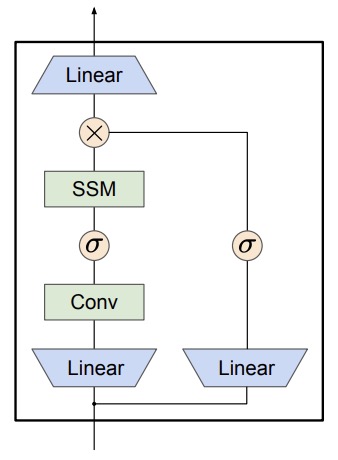
  • Experimental results highlight MambaByte’s superior performance and computational efficiency. Benchmarks on the PG19 dataset and comparisons with other byte-level models, including the MegaByte Transformer and gated diagonalized S4, demonstrated MambaByte’s reduced computational demands and enhanced effectiveness in language modeling tasks. Its capability to maintain competitive performance with significantly longer sequences without relying on tokenization marks a substantial advancement in language model training.
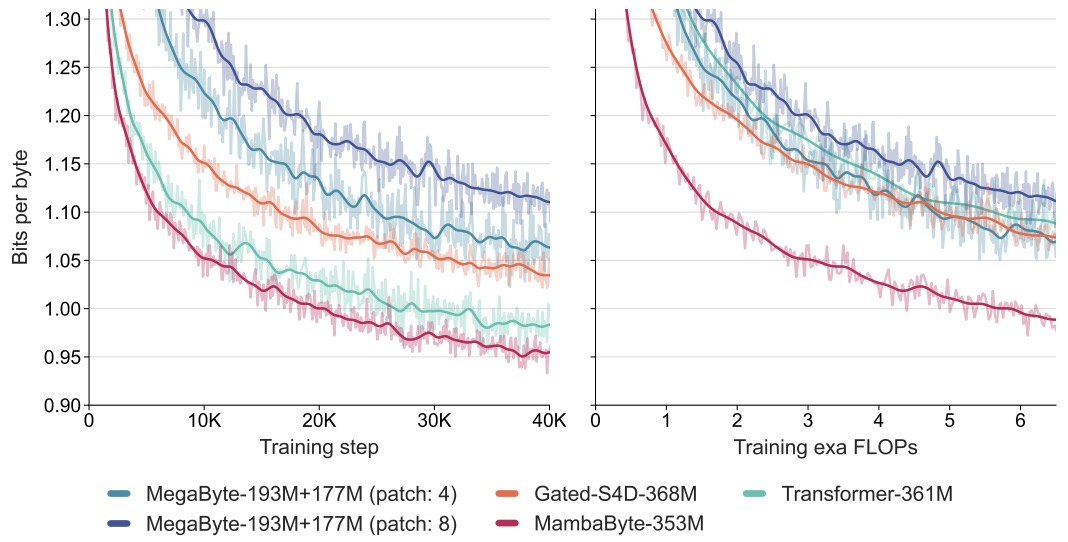
  • The figure below from the paper shows the benchmarking byte-level models with a fixed parameter budget. Language modeling results on PG19 (8, 192 consecutive bytes), comparing the standard Transformer, MegaByte Transformer, gated diagonalized S4, and MambaByte. (Left) Model loss over training step. (Right) FLOP-normalized training cost. MambaByte reaches Transformer loss in less than one-third of the compute budget.

  • The paper provides a comprehensive analysis of the MambaByte model, including its experimental setup, dataset specifics, and detailed implementation techniques. The study meticulously outlines the comparative evaluation of MambaByte against other models under fixed parameter and compute settings across several long-form text datasets. Furthermore, it delves into the selective state space sequence modeling background that underpins MambaByte’s design, offering insights into the model’s operational efficiency and practicality for large-scale language processing tasks.
  • MambaByte’s introduction as a token-free model that effectively addresses the inefficiencies of byte-level processing while rivaling the performance of subword models is a significant contribution to the field of natural language processing. Its development paves the way for future explorations into token-free language modeling, potentially influencing large-scale model training methodologies and applications.
  • Code

Scalable Diffusion Models with State Space Backbone

  • This paper by Fei et al. from Kunlun Inc. introduces a novel approach to scaling diffusion models using a state space architecture.
  • They focus on replacing the traditional U-Net backbone with a state space model (SSM) framework to enhance image generation performance and computational efficiency.
  • The authors present Diffusion State Space Models (DiS) that treat all inputs—time, condition, and noisy image patches—as discrete tokens, enhancing the model’s ability to handle long-range dependencies effectively. The DiS architecture is characterized by its scalability, leveraging state space techniques that offer superior performance compared to conventional CNN-based or Transformer-based architectures, especially in handling larger image resolutions and reducing computational costs.
  • Key Technical Details and Implementation:
    • Architecture: DiS utilizes a state space model backbone which processes inputs as tokens, incorporating forward and backward processing with skip connections that enhance both shallow and deep layers’ integration.
    • Noise Prediction Network: The noise prediction network in DiS, represented as \(\epsilon_\theta(x_t, t, c)\), predicts the injected noise at various timesteps and conditions, thereby optimizing the reverse diffusion process from noisy to clean images.
    • Model Configurations: Different configurations of DiS are explored, with parameters adjusted for varying depths and widths, showing a clear correlation between increased model complexity and improved image quality metrics.
    • Patchify and Linear Decoder: Initial layers transform input images into a sequence of tokens which are then processed by SSM blocks. The output is decoded back to image space using a linear decoder after the final SSM block, predicting noise and covariance matrices.
  • The following figure from the paper shows the proposed state space-based diffusion models. It treats all inputs including the time, condition and noisy image patches as tokens and employs skip connections between shallow and deep layers. Different from original Mamba for text sequence modeling, our SSM block process the hidden states sequence with both forward and backward directions.

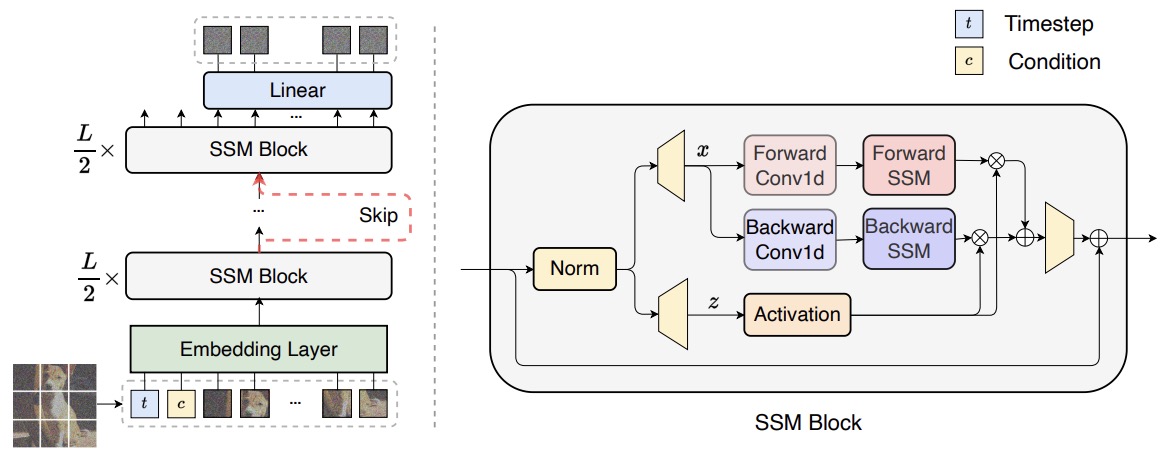
  • DiS models were tested under unconditional and class-conditional image generation tasks. In scenarios like ImageNet at resolutions of 256 \(\times\) 256 and 512 \(\times\) 512 pixels, DiS models demonstrated competitive or superior performance to prior models, achieving impressive Frechet Inception Distance (FID) scores.
  • Various configurations from small to huge models were benchmarked to demonstrate scalability, showing that larger models continue to provide substantial improvements in image quality.
  • The paper concludes that DiS models not only perform comparably or better than existing architectures but do so with less computational overhead, showcasing their potential in scalable and efficient large-scale image generation. This approach paves the way for future explorations into more effective generative modeling techniques that can handle complex, high-resolution datasets across different modalities. The authors also make their code and models publicly available, encouraging further experimentation and development in the community.

Cobra: Extending Mamba to Multi-Modal Large Language Model for Efficient Inference

  • This paper by Zhao et al. from Westlake University and Zhejiang University introduces Cobra, in response to the growing need for efficient multi-modal large language models (MLLMs). This model enhances the efficiency of MLLMs by incorporating a linear computational complexity approach through the use of the state space model (SSM) framework, distinct from the common quadratic complexity of traditional Transformer networks.
  • Cobra extends the Mamba model by integrating visual information processing capabilities. This integration is achieved through a combination of an image encoder and a novel training methodology. The Mamba model, known for its efficient processing relative to Transformer-based models, is enhanced with visual modality by incorporating an image encoder that allows for the efficient handling of visual data.
  • A significant feature of Cobra is its modal fusion approach, which optimizes the interaction between visual and linguistic data. Various fusion schemes were explored, with experiments showing that specific strategies significantly enhance the model’s multi-modal capabilities.
  • The model demonstrates its effectiveness across multiple benchmarks, particularly in tasks like Visual Question Answering (VQA), where it competes robustly against other state-of-the-art models like LLaVA and TinyLLaVA, despite having fewer parameters. For instance, Cobra achieved performance comparable to LLaVA while utilizing only about 43% of LLaVA’s parameters.
  • The architectural design of Cobra includes a combination of DINOv2 and SigLIP as vision encoders, projecting visual information into the language model’s embedding space. This setup not only preserves but enhances the model’s ability to process and understand complex visual inputs alongside textual data.
  • Training adjustments and implementation details reveal a departure from traditional pre-alignment phases used in other models. Instead, Cobra’s approach involves direct fine-tuning of the entire LLM backbone along with the projector over two epochs, which optimizes both efficiency and model performance.
  • The figure below from the paper shows a detailed architecture of Cobra (right) that takes Mamba as the backbone consisting of identical Mamba blocks (left). The parameters of vision encoders are frozen during training.

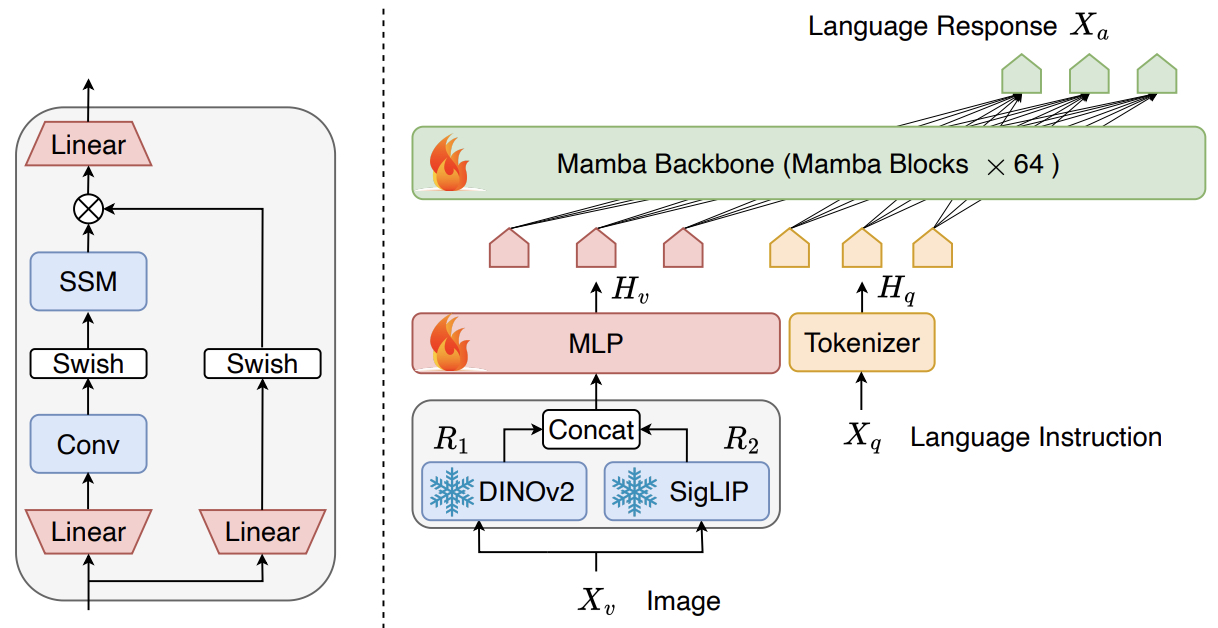
  • Performance metrics from the paper indicate that Cobra is not only faster but also retains high accuracy in interpreting and responding to multi-modal inputs, showing particularly strong capabilities in handling visual illusions and spatial relationships, a testament to its robust visual processing capabilities.
  • Overall, Cobra’s design significantly reduces the computational cost and model complexity while maintaining competitive accuracy and speed, making it a promising solution for applications requiring efficient and effective multi-modal processing.
  • Code

SAMBA: Simple Hybrid State Space Models for Efficient Unlimited Context Language Modeling

  • This paper introduces SAMBA, a novel hybrid architecture that combines Mamba, a selective State Space Model (SSM), with Sliding Window Attention (SWA) to efficiently model sequences with infinite context length. The authors address the challenge of balancing computation complexity and the ability to generalize to longer sequences than seen during training. SAMBA leverages the strengths of both SSMs and attention mechanisms to achieve linear-time complexity while maintaining precise memory recall.
  • SAMBA architecture consists of three main components: Mamba layers, SWA layers, and Multi-Layer Perceptrons (MLPs). Mamba layers capture time-dependent semantics and compress sequences into recurrent hidden states. SWA layers, operating on a window size of 2048, provide precise retrieval of non-Markovian dependencies within the sequence. MLP layers handle nonlinear transformations and recall of factual knowledge, enhancing the model’s overall capability.
  • The SAMBA model was scaled to 3.8B parameters and trained on 3.2T tokens. It demonstrated superior performance compared to state-of-the-art models based on pure attention or SSMs across various benchmarks, including commonsense reasoning, language understanding, truthfulness, and math and coding tasks. Notably, SAMBA showed improved token predictions up to 1M context length and achieved a 3.73× higher throughput than Transformers with grouped-query attention when processing 128K length user prompts.
  • The figure below from the paper illustrates from left to right: Samba, Mamba-SWA-MLP, Mamba-MLP, and Mamba. The illustrations depict the layer-wise integration of Mamba with various configurations of Multi-Layer Perceptrons (MLPs) and Sliding Window Attention (SWA). They assume the total number of intermediate layers to be \(N\), and omit the embedding layers and output projections for simplicity. Pre-Norm and skip connections are applied for each of the intermediate layers.

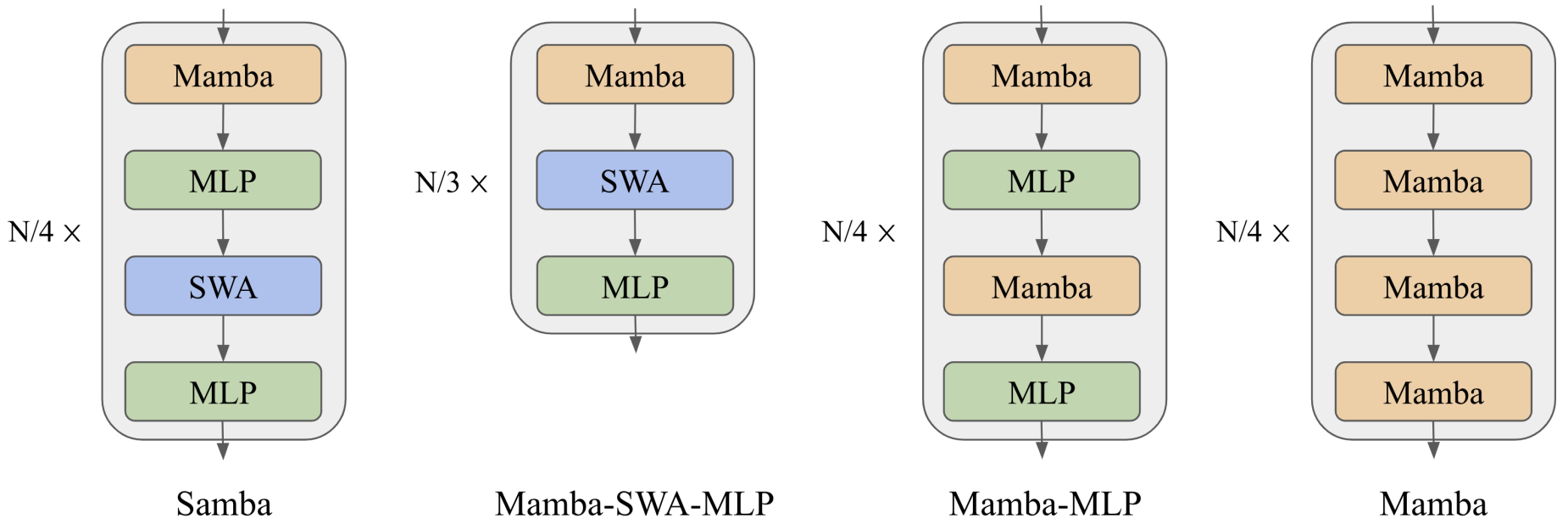
  • The implementation of SAMBA involved meticulous exploration of hybridization strategies, including different layer-wise combinations of Mamba, SWA, and MLP. The final configuration was optimized for performance, with a total of 48 layers for Samba and Mamba-MLP models, and 54 layers for the Mamba-SWA-MLP model. The models were pre-trained on the Phi-2 dataset with 4K sequence lengths, and downstream evaluations were conducted on a range of benchmarks to validate the architectural design.
  • SAMBA’s ability to extrapolate context length was tested extensively. It maintained linear decoding time complexity with unlimited token streaming, achieving perfect memory recall and improved perplexity on long sequences. The model’s performance on long-context summarization tasks further demonstrated its efficiency and effectiveness in handling extensive contexts.
  • In conclusion, SAMBA presents a significant advancement in language modeling, offering a simple yet powerful solution for efficient modeling of sequences with unlimited context length. The hybrid architecture effectively combines the benefits of SSMs and attention mechanisms, making it a promising approach for real-world applications requiring extensive context understanding.
  • Code

Further Reading

SSMs

RWKV

  • Related resources to understand RWKV, another architecture that converts self-attention to a linear operation:
    • Intro to RWKV presents an overview of the RWKV language model, an RNN that combines the benefits of transformers, offering efficient training, reduced memory use during inference, and excellent scaling up to 14 billion parameters, while being an open-source project open for community contribution.
    • Annotated RWKV offers 100 lines of code to implement a basic version of RWKV.

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledStateSpaceModels,
  title   = {State Space Models},
  author  = {Chadha, Aman and Jain, Vinija},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://vinija.ai}}
}