Overview

  • Pre-processing is one of the fundamental steps in the model development lifecycle. The pre-processing step (also known as the data processing step), feature scaling using standardization, normalization, etc. is carried out.
  • Let’s explore feature scaling next.

Feature Scaling

  • In practice, we often encounter different types of variables in the same dataset. A significant issue is that the range of the variables may differ a lot. Using the original scale may put more weights on the variables with a large range.
  • In order to deal with this problem, we need to apply the technique of features rescaling to independent variables or features of data in the step of data pre-processing. The terms normalization and standardization are sometimes used interchangeably, but they usually refer to different things.
  • The goal of feature scaling is to make sure features are on almost the same scale so that each feature is equally important and make the learning process most effective for ML algorithms.

Example

  • The figure below shows a dataset that contains an independent variable (purchased) and 3 dependent variables (Country, Age, and Salary). We can easily notice that the variables are not on the same scale because the range of Age is from 27 to 50, while the range of Salary going from 48K to 83K. The range of Salary is much wider than the range of Age. This will cause some issues in our models since a lot of machine learning models such as k-means clustering and nearest neighbor classification are based on the Euclidean Distance.

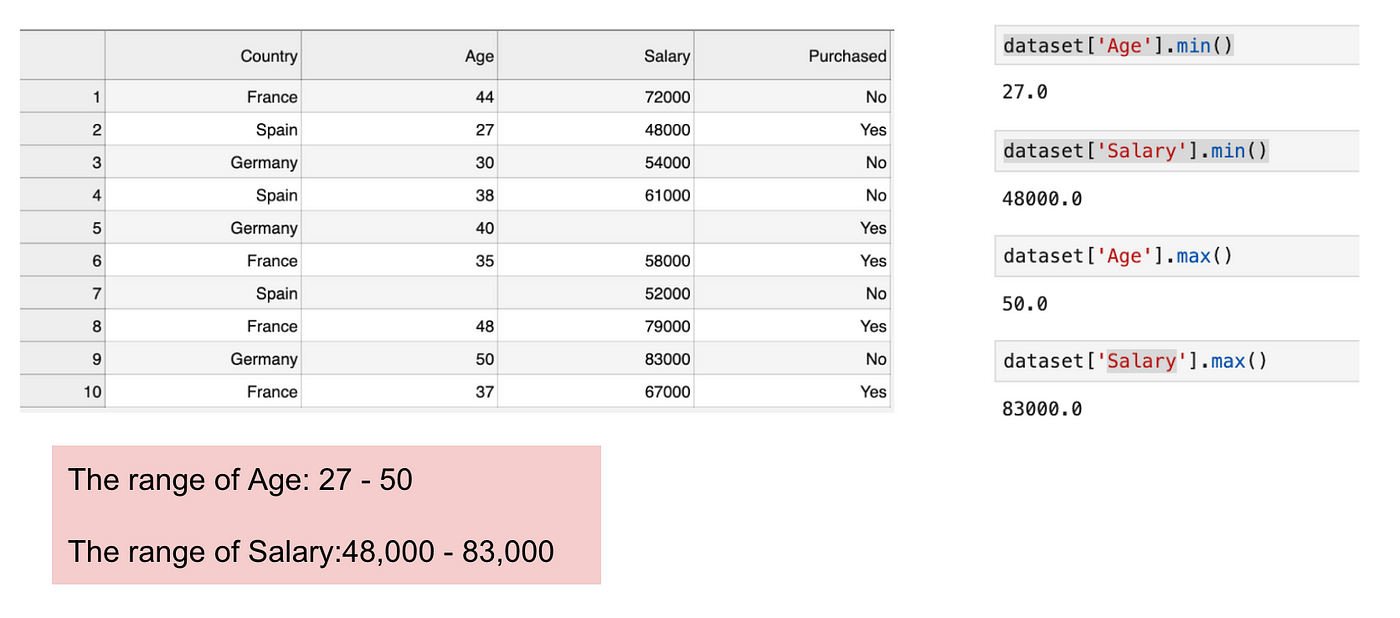
  • When we calculate the equation of Euclidean distance, the number of \((x^2-x^1)^2\) is much bigger than the number of \((y^2-y^1)^2\) which means the Euclidean distance will be dominated by the salary if we do not apply feature scaling. The difference in Age contributes less to the overall difference. Therefore, we should use Feature Scaling to bring all values to the same magnitudes and, thus, solve this issue. To do this, there are primarily two methods called standardization and normalization.

Standardization

  • The result of standardization (or Z-score normalization) is that the features will be rescaled to ensure the mean and the standard deviation to be 0 and 1, respectively. The equation is shown below:
\[x_{\text {stand }}=\frac{x-\operatorname{mean}(x)}{\text { standard deviation }(x)}\]
  • This technique is to re-scale features value with the distribution value between 0 and 1 is useful for the optimization algorithms, such as gradient descent, that are used within machine learning algorithms that weight inputs (e.g., regression and neural networks). Rescaling is also used for algorithms that use distance measurements, for example, K-Nearest-Neighbours (KNN).
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
sc_X = sc_X.fit_transform(df)

# convert to table format - StandardScaler 
sc_X = pd.DataFrame(data=sc_X, columns=["Age", "Salary","Purchased","Country_France","Country_Germany", "Country_spain"])
sc_X

Max-Min Normalization

  • Another common approach is the so-called max-min normalization (min-max scaling). This technique is to re-scales features with a distribution value between 0 and 1. For every feature, the minimum value of that feature gets transformed into 0, and the maximum value gets transformed into 1. The general equation is shown below:
\[x_{\text {norm }}=\frac{x-\min (x)}{\max (x)-\min (x)}\] 
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(df)
scaled_features = scaler.transform(df)

# convert to table format - MinMaxScaler
df_MinMax = pd.DataFrame(data=scaled_features, columns=["Age", "Salary","Purchased","Country_France","Country_Germany", "Country_spain"])

Standardization vs. Max-Min Normalization

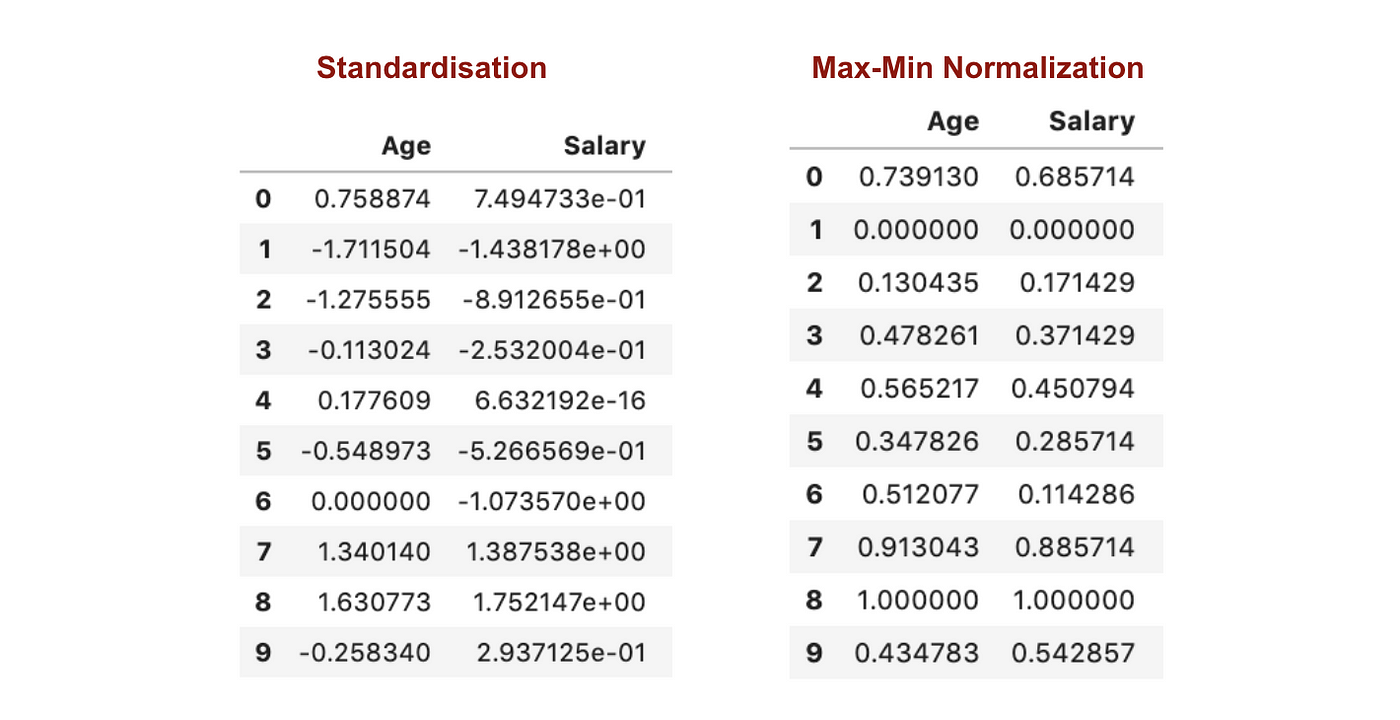
  • In contrast to standardization, we will obtain smaller standard deviations through the process of max-min normalization. Let’s illustrate this using the above dataset post feature scaling:

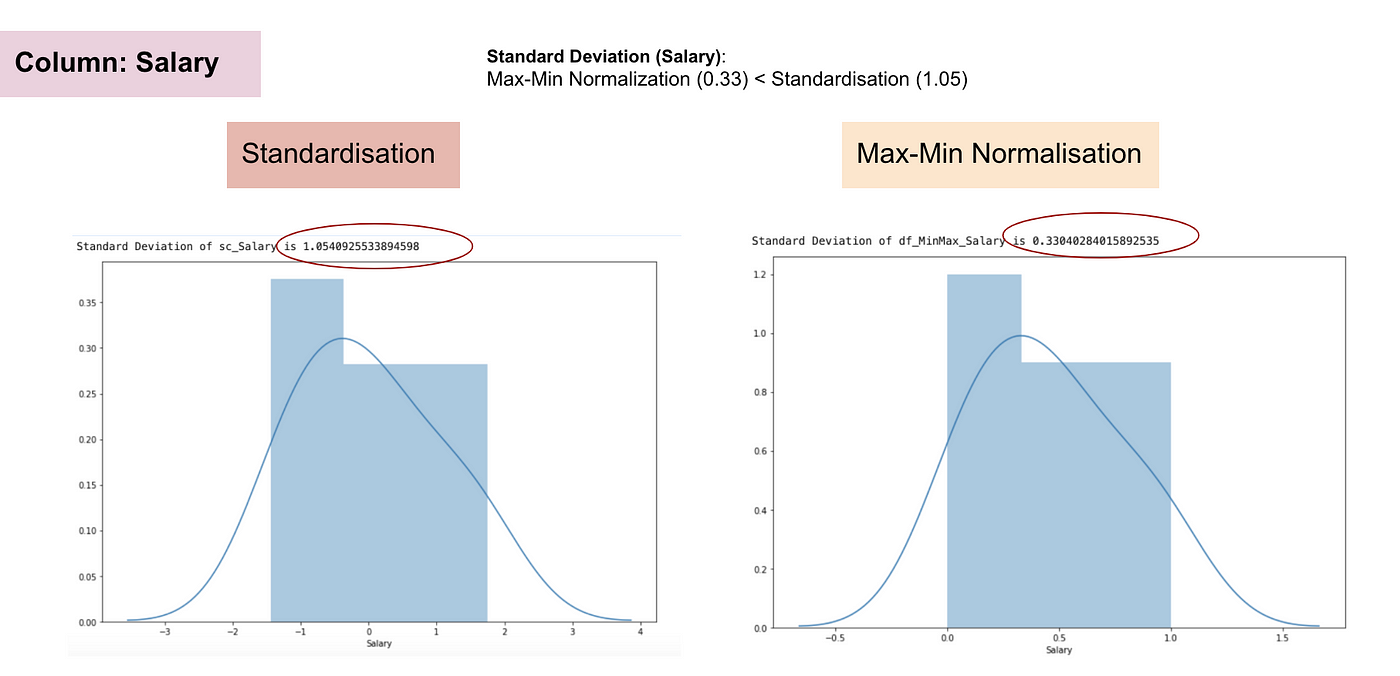
  • The following plots show the normal distribution and standard deviation of salary:

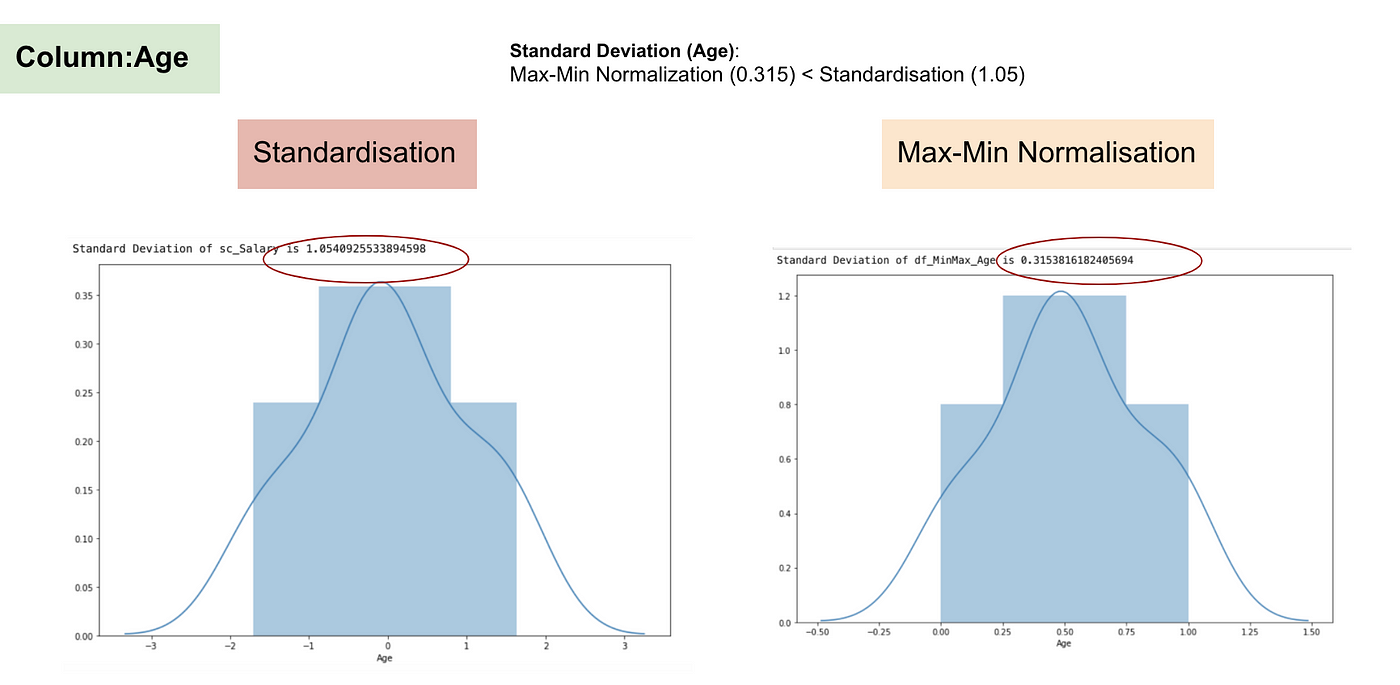
  • The following plots show the normal distribution and standard deviation of age:

  • From the above graphs, we can clearly notice that applying max-min normalization in our dataset has generated smaller standard deviations (Salary and Age) than using standardization method. It implies the data are more concentrated around the mean if we scale data using max-min normalization.

  • As a result, if you have outliers in your feature (column), normalizing your data will scale most of the data to a small interval, which means all features will have the same scale but does not handle outliers well. Standardization is more robust to outliers, and in many cases, it is preferable over max-min normalization.

When Feature Scaling Matters

  • Some machine learning models are fundamentally based on distance matrix, also known as the distance-based classifier, for example, k nearest neighbors, SVM, and Neural Network. Feature scaling is extremely essential to those models, especially when the range of the features is very different. Otherwise, features with a large range will have a large influence in computing the distance.

  • Max-min normalization typically allows us to transform the data with varying scales so that no specific dimension will dominate the statistics, and it does not require making a very strong assumption about the distribution of the data, such as k-nearest neighbors and artificial neural networks. However, normalization does not treat outliners very well. On the contrary, standardization allows users to better handle the outliers and facilitate convergence for some computational algorithms like gradient descent. Therefore, we usually prefer standardization over Min-Max normalization.

Algorithms the benefit the most from feature scaling

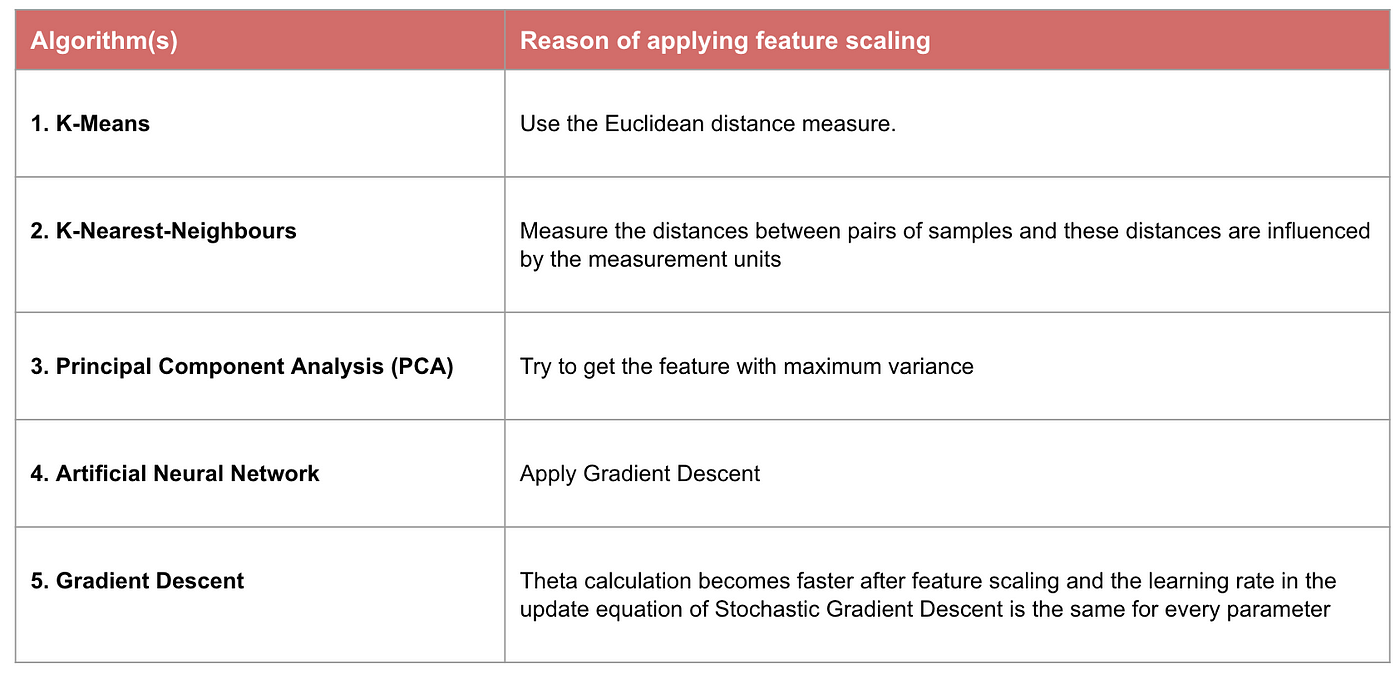
  • Note: If an algorithm is not distance-based, feature scaling is unimportant, including Naive Bayes, linear discriminant analysis, and tree-based models (gradient boosting, random forest, etc.).

References

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledKernelTrick,
  title   = {Kernel Trick},
  author  = {Chadha, Aman},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}