Overview

  • Reinforcement Learning (RL) is a type of machine learning where an agent learns to make sequential decisions by interacting with an environment. The goal of the agent is to maximize cumulative rewards over time by learning which actions yield the best outcomes in different states of the environment. Unlike supervised learning, where models are trained on labeled data, RL focuses on exploration and exploitation: the agent must explore various actions to discover high-reward strategies while exploiting what it has learned to achieve long-term success.

  • In RL, the agent, environment, actions, states, and rewards are fundamental components. At each step, the agent observes the state of the environment, chooses an action based on its policy (its strategy for selecting actions), and receives a reward that guides future decision-making. The agent’s objective is to learn a policy that maximizes the expected cumulative reward, typically by using techniques such as dynamic programming, Monte Carlo methods, or temporal-difference learning.

  • Deep RL extends traditional RL by leveraging deep neural networks to handle complex environments with high-dimensional state spaces. This allows agents to learn directly from raw, unstructured data, such as pixels in video games or sensors in robotic control. Deep RL algorithms, like Deep Q-Networks (DQN) and policy gradient methods (e.g., Proximal Policy Optimization, PPO), have achieved breakthroughs in domains like playing video games at superhuman levels, robotics, and autonomous driving.

  • This primer provides an introduction to the foundational concepts of RL, explores key algorithms, and outlines how deep learning techniques enhance the power of RL to tackle real-world, high-dimensional problems.

Basics of Reinforcement Learning

  • RL is a type of machine learning where an agent learns to make decisions by interacting with an environment. Unlike supervised learning, where a model learns from a fixed dataset of labeled examples, RL focuses on learning from the consequences of actions rather than from predefined correct behavior. The interaction between the agent and the environment is guided by the concepts of states, actions, rewards, and policies, which form the foundation of RL. The agent seeks to maximize cumulative rewards by exploring different actions and learning which ones yield the best outcomes over time.

  • Deep RL extends this framework by incorporating neural networks to handle high-dimensional, complex problems that traditional RL methods struggle with. By using deep learning techniques, Deep RL can tackle challenges like visual input or other high-dimensional data, allowing it to solve problems that are intractable for classical RL approaches. This combination of RL and neural networks enables agents to perform well in more complex environments with minimal manual intervention.

Key Components of Reinforcement Learning

  • At the core of RL is the interaction between an agent and an environment, as shown in the diagram below (source):

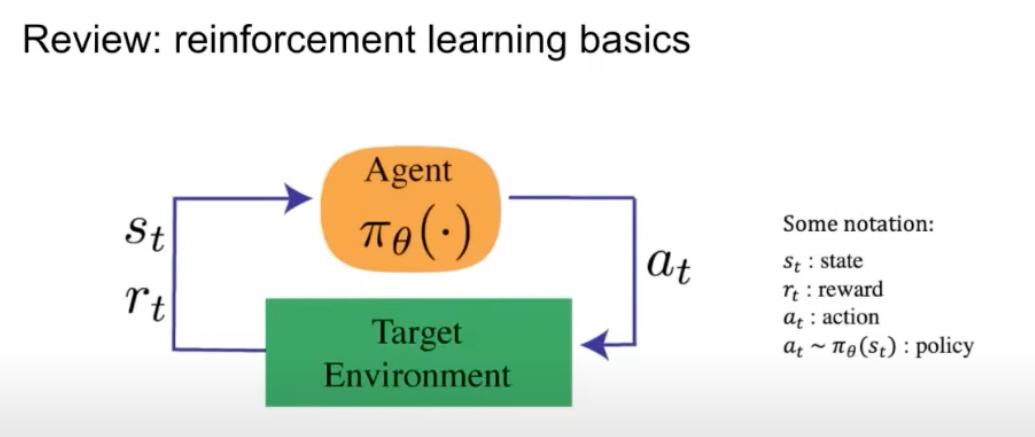
  • In this interaction, the agent takes actions in the environment and receives feedback in the form of states and rewards. The goal is for the agent to learn a strategy, or policy, that maximizes the cumulative reward over time.

  • Here are the critical components of RL:

    1. Agent/Learner: The agent is the learner or decision-maker. It is responsible for selecting actions based on the current state of the environment.

    2. Environment: Everything the agent interacts with. The environment defines the rules of the game, transitioning from one state to another based on the agent’s actions.

    3. State (s): A representation of the environment at a particular point in time. States encapsulate all the information that the agent needs to know to make a decision. For example, in a video game, a state might be the current configuration of the game board.

    4. Action (a): A decision taken by the agent in response to the current state. In each state, the agent must choose an action from a set of possible actions, which will affect the future state of the environment.

    5. Reward (r): A scalar value that the agent receives from the environment after taking an action. The reward provides feedback on how good or bad an action was in that particular state. The agent’s objective is to maximize the cumulative reward over time, often referred to as the return.

    6. Policy (π): A policy is the strategy the agent uses to determine the actions to take based on the current state. It can be a simple lookup table mapping states to actions, or it can be more complex, such as a neural network in the case of deep RL. The policy can be deterministic (always taking the same action for a given state) or stochastic (taking different actions with some probability).

    7. Value Function: This function estimates how good it is to be in a particular state (or to take a specific action in that state). The value function helps the agent understand long-term reward potential rather than focusing only on immediate rewards.

The Bellman Equation

  • The Bellman Equation is a fundamental concept in RL, used to describe the relationship between the value of a state and the value of its successor states. It breaks down the value function into immediate rewards and the expected value of future states.

  • For a given policy \(\pi\), the state-value function \(V^\pi(s)\) can be written as:

    \[V^\pi(s) = \mathbb{E}_\pi \left[ r_t + \gamma V^\pi(s_{t+1}) \mid s_t = s \right]\]

    where:

    • \(V^\pi(s)\) is the value of state \(s\) under policy \(\pi\),
    • \(r_t\) is the reward received after taking an action at time \(t\),
    • \(\gamma\) is the discount factor (0 ≤ \(\gamma\) ≤ 1) that determines the importance of future rewards,
    • \(s_{t+1}\) is the next state after taking an action from state \(s\).

  • This equation expresses that the value of a state \(s\) is the immediate reward \(r_t\) plus the discounted value of the next state \(V^\pi(s_{t+1})\). The Bellman equation is central to many RL algorithms, as it provides the basis for recursively solving the optimal value function.

The RL Process: Trial and Error Learning

  • The agent interacts with the environment in a loop:
    1. At each time step, the agent observes the current state of the environment.
    2. Based on this state, it selects an action according to its policy.
    3. The environment transitions to a new state, and the agent receives a reward.
    4. The agent uses this feedback to update its policy, gradually improving its decision-making over time.
  • This process of learning from trial and error allows the agent to explore different actions and outcomes, eventually finding the optimal policy that maximizes the long-term reward.

Mathematical Formulation: Markov Decision Process (MDP)

  • RL problems are typically framed as Markov Decision Processes (MDP), which provide a mathematical framework for modeling decision-making where outcomes are partly random and partly under the control of the agent. An MDP is defined by:
    • States (S): The set of all possible states in the environment.
    • Actions (A): The set of all possible actions the agent can take.
    • Transition function (P): The probability distribution of moving from one state to another, given an action.
    • Reward function (R): The immediate reward received after transitioning from one state to another.
    • Discount factor (γ): A factor between 0 and 1 that determines the importance of future rewards. A discount factor close to 0 prioritizes immediate rewards, while a value close to 1 encourages the agent to consider long-term rewards.

  • The agent’s goal is to learn a policy \(\pi(s)\) that maximizes the expected cumulative reward or return, often expressed as:

    \[G_t = \sum_{k=0}^{\infty} \gamma^k r_{t+k+1}\]
    • where:
      • \(G_t\) is the total return starting from time step \(t\),
      • \(\gamma\) is the discount factor,
      • \(r_{t+k+1}\) is the reward received at time \(t+k+1\).

Deep Reinforcement Learning

  • As environments grow in complexity, traditional RL methods face challenges in scalability and handling high-dimensional state and action spaces. This is where Deep RL becomes essential. Deep RL leverages deep neural networks to approximate complex policies and value functions, enabling RL to be applied to problems with large and continuous state spaces, such as video games, robotics, and autonomous driving. By combining the representational power of deep learning with the decision-making framework of RL, Deep RL algorithms have achieved significant breakthroughs across various domains.

Key Algorithms in Deep RL

  1. Deep Q-Network (DQN): DQN was a pioneering algorithm in the Deep RL space, combining Q-learning with deep neural networks to approximate the Q-value function, which estimates the expected future rewards for taking specific actions in a given state. DQN has been successfully applied to various Atari games, such as Pong, where the state space is too large to represent explicitly (e.g., raw pixel inputs). DQN also incorporates techniques like experience replay and target networks to stabilize learning, making it a strong starting point for many Deep RL tasks.

  2. Policy Gradient Methods: While DQN is a value-based method, policy gradient (PG) methods directly optimize the policy function, which maps states to actions. PG methods are particularly useful in environments with continuous action spaces, where the agent must choose actions from a range of values rather than a discrete set. Algorithms like REINFORCE, Proximal Policy Optimization (PPO), and Trust Region Policy Optimization (TRPO) are popular examples. These methods provide a stable way to optimize policies for long-term reward maximization.

  3. Actor-Critic Methods (A2C, A3C, PPO): Actor-Critic methods combine the strengths of both policy-based and value-based approaches. In these algorithms, an actor network selects actions, while a critic network estimates the value function to evaluate how good the chosen actions are. This dual structure can improve sample efficiency and performance. Popular algorithms such as Advantage Actor-Critic (A2C), Asynchronous Advantage Actor-Critic (A3C), and Proximal Policy Optimization (PPO) have been widely adopted for their stability and efficiency, with PPO being particularly popular for its balance of ease of use and strong performance across various tasks.

  4. Evolutionary Strategies (ES): Evolutionary Strategies are a family of black-box optimization algorithms that can be used for RL. Unlike gradient-based methods, ES doesn’t require careful tuning of learning rates and is robust in handling sparse or delayed rewards. OpenAI has successfully used ES to train agents to play games like Pong, offering a different perspective on how optimization can be approached in RL tasks.

  5. Monte Carlo Tree Search (MCTS): Monte Carlo Tree Search is a planning algorithm that has been highly successful in games with large action spaces, such as Go and chess. It builds a search tree by simulating different actions and their outcomes. DeepMind’s AlphaZero famously used MCTS in combination with deep learning to master games like Go, Chess, and Shogi, showcasing the power of combining search algorithms with neural networks.

Practical Considerations

  • The performance of these algorithms can vary based on the complexity of the environment, the nature of the state and action spaces, and available computational resources. For beginners, it’s recommended to start with algorithms like DQN or PPO due to their stability and ease of use. Experimentation and tuning are often necessary to find the best algorithm for a specific task, and tools like OpenAI Gym for simulation environments and RLlib for production-level distributed RL workloads can be invaluable for streamlining development.
  • By integrating deep learning with RL, Deep RL has opened up new possibilities for solving complex decision-making problems, pushing the boundaries of AI in fields such as gaming, robotics, and autonomous systems.

Policy Evaluation

  • Evaluating RL policies is a critical step in ensuring that the learned policies perform effectively when deployed in real-world applications. Unlike supervised learning, where models are evaluated on static test sets, RL presents unique challenges due to its interactive nature and the stochasticity of the environment. This makes policy evaluation both crucial and non-trivial.

  • Offline Policy Evaluation (OPE) methods, such as the Direct Method, Importance Sampling, and Doubly Robust approaches, are essential tools for safely evaluating RL policies without direct interaction with the environment. Each method comes with trade-offs between bias, variance, and data efficiency, with hybrid approaches like Doubly Robust often providing the best balance. Accurate policy evaluation is fundamental for deploying RL in real-world systems where safety, reliability, and efficiency are of utmost importance.

  • Policy evaluation in RL can be broken into two main categories:

    1. Online Policy Evaluation: This involves evaluating a policy while interacting with the environment in real time. It provides direct feedback on how the policy performs under real conditions, but it can be risky and expensive, especially in sensitive or costly domains like healthcare, robotics, or finance.

    2. Offline Policy Evaluation (OPE): This is the evaluation of RL policies using logged data, without further interactions with the environment. OPE is crucial in situations where deploying a poorly performing policy would be dangerous, expensive, or unethical.

Online Policy Evaluation

  • In online policy evaluation, the policy is tested in the environment to observe its real-time performance. Common metrics include:

    • Expected Return: The most common measure in RL, defined as the expected cumulative reward (discounted or undiscounted) obtained by following the policy over time. This is expressed as:

      \[J(\pi) = \mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, a_t)\right]\]

      where:

      • \(\pi\) is the policy,
      • \(R(s_t, a_t)\) is the reward obtained at time step \(t\),
      • \(\gamma\) is the discount factor (0 ≤ γ ≤ 1),
      • and the expectation is taken over all possible trajectories the policy might follow.

    • Sample Efficiency: RL methods often require many interactions with the environment to train, and sample efficiency measures how well a policy performs given a limited number of interactions.

    • Stability and Robustness: Evaluating if the policy consistently achieves good performance under different conditions or in the presence of uncertainties, such as noise in the environment or policy execution errors.

  • However, real-world deployment of RL agents might come with risks. For instance, in healthcare, trying an untested policy could harm patients. Hence, the need for offline policy evaluation (OPE) arises.

Offline Policy Evaluation (OPE)

  • Offline Policy Evaluation aims to estimate the performance of a new or learned policy using data collected by some behavior policy (i.e., an earlier or different policy used for gathering data). OPE methods allow us to estimate the performance without executing the policy in the real environment.

Key Challenges in OPE

  • Distribution Mismatch: The behavior policy that generated the data might be very different from the target policy we are evaluating. This can cause inaccuracies because the data may not cover the state-action space sufficiently for the new policy.
  • Confounding Bias: Logged data can introduce bias when certain actions or states are under-sampled or never seen in the dataset, which leads to poor estimation of the target policy.

Common OPE Methods

Direct Method (DM)

  • The direct method uses a supervised learning model (such as a regression model) to estimate the expected rewards for state-action pairs based on the data from the behavior policy. Once the model is trained, it is used to predict the rewards the target policy would obtain.
  • Steps:
    • Train a model \(\hat{R}(s,a)\) using logged data to predict the reward for any state-action pair.
    • Simulate the expected return of the target policy by averaging over the predicted rewards for actions it would take under different states in the dataset.
  • Advantages:
    • Simple and easy to implement.
    • Can generalize to new state-action pairs not observed in the logged data.
  • Disadvantages:
    • Sensitive to model accuracy, and any modeling error can lead to incorrect estimates.
    • Can suffer from extrapolation errors if the target policy takes actions that are very different from the logged data.

Importance Sampling (IS)

  • Importance sampling is one of the most widely used methods in OPE. It reweights the rewards in the logged data by the likelihood ratio between the target policy and the behavior policy. The intuition is that the rewards observed from the behavior policy are “corrected” to reflect what would have happened if the target policy had been followed.

    \[\hat{J}(\pi) = \sum_{i=1}^{N} \frac{\pi(a_i|s_i)}{\mu(a_i|s_i)} R(s_i, a_i)\]
    • where \(\mu(a_i\|s_i)\) is the probability of the action \(a_i\) being taken under the behavior policy, and \(\pi(a_i\|s_i)\) is the probability under the target policy.
  • Advantages:
    • Does not require a model of the reward or transition dynamics, only knowledge of the behavior policy.
    • Corrects for the distribution mismatch between the behavior policy and the target policy.
  • Disadvantages:
    • High variance when the behavior and target policies differ significantly.
    • Prone to large importance weights that dominate the estimation, making it unstable for long horizons.

Doubly Robust (DR)

  • The doubly robust method combines the direct method (DM) and importance sampling (IS) to leverage the strengths of both. It reduces the variance compared to IS and the bias compared to DM. The DR estimator uses a model to estimate the reward (as in DM), but it also uses importance sampling to adjust for any inaccuracies in the model.

  • The DR estimator can be expressed as:

    \[\hat{J}(\pi) = \sum_{i=1}^{N} \left( \frac{\pi(a_i|s_i)}{\mu(a_i|s_i)}(R(s_i, a_i) - \hat{R}(s_i, a_i)) + \hat{R}(s_i, a_i)\right)\]
  • Advantages:
    • More robust than either DM or IS alone.
    • Can handle both distribution mismatch and modeling errors better than individual methods.
  • Disadvantages:
    • Requires both a well-calibrated model and a reasonable importance weighting scheme.
    • Still sensitive to extreme weights in cases where the behavior policy is very different from the target policy.

Fitted Q-Evaluation (FQE)

  • FQE is a model-based OPE approach that estimates the expected return of the target policy by first learning the Q-values (state-action values) for the policy. It involves solving the Bellman equations iteratively over the logged data to approximate the value function of the policy. Once the Q-function is learned, the value of the target policy can be computed by evaluating the actions it would take at each state.

  • Advantages:
    • Can work well when the Q-function is learned accurately from the data.
  • Disadvantages:
    • Requires solving a complex optimization problem.
    • May suffer from overfitting or underfitting depending on the quality of the data and the model.

Model-based Evaluation

  • This involves constructing a model of the environment (i.e., transition dynamics and reward function) based on the logged data. The performance of a policy is then simulated within this learned model. A model-based evaluation can give insights into how the policy performs over a wide range of scenarios. However, it can be highly sensitive to inaccuracies in the model.

Challenges of Reinforcement Learning

While Reinforcement Learning (RL) has shown remarkable successes, particularly when combined with deep learning, it also faces several challenges that limit its widespread application in real-world settings. These challenges include issues related to exploration, sample efficiency, stability, scalability, and safety.

Challenges of Reinforcement Learning

  • While RL has shown remarkable successes, particularly when combined with deep learning, it faces several challenges that limit its widespread application in real-world settings. These challenges include exploration, sample efficiency, stability, scalability, safety, and generalization. Research into improving these aspects is critical to unlocking the full potential of RL.
  • While solutions such as model-based approaches, distributed RL, and safe RL are actively being explored, significant progress is still needed to overcome these hurdles and enable more reliable, scalable, and safe deployment of RL systems in real-world scenarios.

Exploration vs. Exploitation Dilemma

  • One of the most fundamental challenges in RL is the balance between exploration and exploitation. The agent must explore new actions and strategies to discover potentially higher rewards, but it must also exploit known strategies that provide good rewards. Striking the right balance between exploring the environment and exploiting accumulated knowledge is a non-trivial problem, especially in environments where exploration may be costly, dangerous, or inefficient.
  • Potential issues:
    • Over-exploration: Wasting time on actions that do not yield significant rewards.
    • Under-exploration: Missing better strategies because the agent sticks to known, sub-optimal actions.
  • Solutions like ε-greedy policies, upper-confidence-bound (UCB) algorithms, and Thompson sampling attempt to address this dilemma, but optimal balancing remains an open problem.

Sample Inefficiency

  • RL algorithms often require vast amounts of data to learn effective policies. This is particularly problematic in environments where data collection is expensive, slow, or impractical (e.g., robotics, healthcare, or autonomous driving). For instance, training an RL agent to control a physical robot requires many iterations, and any missteps can damage hardware or cause safety risks.
  • Deep RL algorithms, such as DQN and PPO, have somewhat mitigated this by utilizing techniques like experience replay, but achieving sample efficiency remains a major challenge. Even state-of-the-art methods can require millions of interactions with the environment to converge on effective policies.

Sparse and Delayed Rewards

  • Many real-world RL problems involve sparse or delayed rewards, where the agent does not receive immediate feedback for its actions. For example, in a game or task where success is only achieved after many steps, the agent may struggle to learn the relationship between early actions and eventual rewards.
  • Potential issues:
    • Difficulty in credit assignment: Identifying which actions were responsible for receiving a reward when the reward signal is delayed over many time steps.
    • Inefficient learning: The agent may require many trials to stumble upon the sequence of actions that lead to reward, prolonging the learning process.
  • Techniques like reward shaping, where intermediate rewards are designed to guide the agent, and temporal credit assignment mechanisms, like eligibility traces, aim to alleviate this issue, but general solutions are still lacking.

High-Dimensional State and Action Spaces

  • Real-world environments often have high-dimensional state and action spaces, making it difficult for traditional RL algorithms to scale effectively. For example, controlling a humanoid robot involves learning in a vast continuous action space with many degrees of freedom.
  • Challenges:
    • Computational Complexity: Searching through high-dimensional spaces exponentially increases the difficulty of finding optimal policies.
    • Generalization: Policies learned in one high-dimensional environment often fail to generalize to similar tasks, necessitating retraining for even minor changes in the task or environment.
  • Deep RL approaches using neural networks have been instrumental in tackling high-dimensional problems, but scalability and generalization across different tasks remain challenging.

Long-Term Dependencies and Credit Assignment

  • Many RL tasks involve long-term dependencies, where actions taken early in an episode affect outcomes far into the future. Identifying which actions were beneficial or detrimental over extended time horizons is difficult due to the complexity of the temporal credit assignment.
  • Potential issues:
    • Vanishing gradients in policy gradient methods can make it hard to propagate the influence of early actions on long-term rewards.
    • In many practical applications, this can lead to sub-optimal policies that favor immediate rewards over delayed but more substantial rewards.
  • Solutions like temporal difference (TD) learning, which bootstraps from future rewards, help address this issue, but they still struggle in environments with long-term dependencies.

Stability and Convergence

  • RL algorithms can be unstable during training, particularly when combining them with neural networks in Deep RL. This instability often arises from non-stationary data distributions, overestimation of Q-values, or large updates to the policy.
  • Potential issues:
    • Divergence: In some cases, the algorithm may fail to converge at all, especially in more complex environments with high variability.
    • Sensitivity to Hyperparameters: Many RL algorithms are highly sensitive to hyperparameter settings like learning rate, discount factor, and exploration-exploitation trade-offs. Tuning these parameters requires extensive experimentation, which may be impractical in many domains.
  • Techniques like target networks (in DQN) and trust region methods (in PPO and TRPO) have been developed to address instability, but robustness across different tasks and environments is still not fully guaranteed.

Safety and Ethical Concerns

  • In certain applications, the exploration required for RL may introduce safety risks. For example, in autonomous vehicles, allowing the agent to explore dangerous or unknown actions could result in harmful accidents. Similarly, in healthcare, deploying untested policies can have severe consequences.
  • Ethical challenges:
    • Balancing exploration without causing harm or incurring excessive cost.
    • Ensuring fairness and avoiding biased decisions when RL algorithms interact with people or sensitive systems.
  • Safe RL, which aims to ensure that agents operate within predefined safety constraints, is an active area of research. However, designing algorithms that guarantee safe behavior while still learning effectively is a difficult challenge.

Generalization and Transfer Learning

  • One of the significant hurdles in RL is that agents trained in one environment often struggle to generalize to new or slightly different environments. For example, an agent trained to play one level of a video game may perform poorly when confronted with a new level with a similar structure.
  • Challenges:
    • Domain adaptation: Policies learned in one domain often fail to generalize to related domains without extensive retraining.
    • Transfer learning: While transfer learning has shown promise in supervised learning, applying it effectively in RL is still challenging due to the unique structure of RL tasks.
  • Research into transfer RL and meta-RL aims to develop agents that can quickly adapt to new environments or learn general policies that apply across multiple tasks, but this remains an evolving area.

Computational Resources and Scalability

  • Training RL models, especially deep RL models, can be computationally expensive. The training process often requires significant computational power, including the use of GPUs or TPUs for large-scale simulations and experiments.
  • Challenges:
    • Hardware Requirements: Training sophisticated RL agents in complex environments, such as 3D simulations or high-resolution video games, demands substantial computational resources.
    • Parallelization: While parallelizing environment interactions can speed up learning, many RL algorithms do not naturally parallelize well, limiting their scalability.
  • Tools like OpenAI’s Distributed Proximal Policy Optimization (DPPO) and Ray RLlib aim to address these issues by enabling scalable, distributed RL, but efficient use of resources remains a challenge.

Reward Function Design

  • Designing the reward function is a crucial and challenging part of RL. An improperly designed reward function can lead to unintended behavior, where the agent optimizes for a reward that doesn’t align with the true objective.
  • Challenges:
    • Reward Hacking: Agents may exploit loopholes in the reward function to achieve high rewards without performing the intended task correctly.
    • Misaligned Objectives: In complex tasks, defining a reward that accurately captures the desired behavior can be extremely difficult.
  • Approaches such as inverse reinforcement learning (IRL), where the agent learns the reward function from expert demonstrations, and reward shaping are used to mitigate these issues, but finding robust solutions remains difficult.

References

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledRL,
  title   = {Reinforcement Learning},
  author  = {Chadha, Aman},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}