Overview

  • Reinforcement Fine-Tuning (RFT) represents a transformative approach to customizing and refining Large Language Models (LLMs). Unlike conventional methods that rely heavily on extensive labeled datasets, RFT leverages Reinforcement Learning (RL) principles to guide model behavior through reward signals. These rewards are assigned to model outputs based on their correctness, enabling the model to optimize its reasoning and accuracy dynamically.

  • RFT is particularly advantageous because it enables domain-specific performance enhancements with significantly fewer training examples. While traditional Supervised Fine-Tuning (SFT) requires thousands of prompt-response pairs to train effectively, RFT has demonstrated the ability to achieve comparable or superior results with as few as a dozen high-quality examples. This makes it ideal for specialized applications where data is limited but the correctness of responses can be objectively/automatically verified.

  • One of the core strengths of RFT is its ability to improve reasoning. Rather than simply learning to mimic correct responses, the model is encouraged to explore, evaluate, and refine strategies that lead to accurate answers. This characteristic is particularly powerful in fields such as law, finance, medicine, and engineering, where nuanced understanding and logical consistency are more important than stylistic mimicry.

  • The emergence of RFT has sparked widespread interest across industries, with organizations leveraging its capabilities to develop expert-level AI assistants, automate complex workflows, and even generate optimized GPU code. As adoption grows, RFT is poised to redefine the landscape of model fine-tuning, enabling more intelligent, adaptable, and efficient AI systems.

How does Reinforcement Fine-Tuning help?

  • RFT addresses several critical limitations of SFT techniques. Most notably, it eliminates the need for large volumes of labeled data, which are often expensive and time-consuming to collect. Instead, RFT relies on verifiable correctness—a mechanism that determines whether a given output meets the task’s success criteria. Furthermore, because RFT is based on RL, it traverses a potentially large search space for valid solutions by balancing exploration of new solutions with exploiting proven approaches.

  • This approach is especially impactful in domains where outputs can be validated programmatically. For example, in tasks such as code transpilation, game playing, or logic puzzles, correctness can be determined by running test cases, comparing outputs to ground truth solutions, or observing objective outcomes. This enables RFT to be deployed in scenarios that would be infeasible with supervised methods.

  • Moreover, RFT improves reasoning capabilities. It allows models to experiment with different strategies and discover more effective reasoning chains through exploration. This is in stark contrast to SFT, which limits the model’s learning to patterns found in the static training data.

  • Finally, RFT promotes better generalization. By focusing on reward-based learning rather than explicit mimicry, models trained via RFT are less prone to overfitting, especially when data is scarce. This makes RFT not only more flexible but also more robust in real-world applications.

Supervised Fine-Tuning vs. Reinforcement Fine-Tuning

  • Although SFT and RFT share the same high-level goal of refining base models for better task-specific performance, the underlying philosophies and mechanics of these approaches differ significantly.

Supervised Fine-Tuning

  • Supervised Fine-Tuning has been the cornerstone of LLM customization for years. In this approach, models are trained on a fixed dataset of prompt-completion pairs. The objective is to adjust the model weights such that the output increasingly resembles the provided completions. This training process is offline, meaning that the dataset remains unchanged throughout the training run.

  • SFT is most effective when ample high-quality data is available. It is well-suited for teaching models new styles, formats, or domain-specific language through imitation. However, this strength becomes a weakness in low-data scenarios. With limited training examples, models often overfit—mimicing/memorizing individual examples instead of learning underlying patterns.

  • Additionally, SFT is fundamentally constrained by its design: the model cannot improve beyond the scope of its labeled data. This limits its potential for learning more complex reasoning or adapting to ambiguous tasks where the best answer isn’t always explicitly shown in the training data.

Reinforcement Fine-Tuning

  • RFT, in contrast, is an online learning process that actively involves the model in exploration and adaptation. Instead of static labels, RFT uses reward functions to guide learning. These functions assess the quality of generated responses based on predefined correctness criteria, enabling the model to iteratively refine its behavior.

Unlike SFT, RFT does not explicitly require labeled data, but it does require that you have a way to objectively determine (via an algorithm) whether the generated output is “correct” or “incorrect”. In the simplest case—where labeled data does exist—this can be as straightforward as checking whether the model’s output exactly matches the ground truth response. For example, in a math problem or string transformation task, a programmatic check can confirm whether the predicted result is accurate.

  • However, the real strength of RFT lies in its broader applicability. It can be deployed even in cases where exact output labels are unknown or impractical to define. For instance, in code generation tasks, we may not know the correct implementation of a function, but we can verify correctness by executing the output against a test suite. In retrieval tasks, we may not have a gold response, but we can measure performance based on whether a relevant document was ranked highly.

  • This makes RFT particularly well-suited to tasks where evaluation is easier than supervision—a common scenario in scientific computing, system design, optimization problems, and real-world deployment environments. By transforming a task into one where outputs can be programmatically validated—even if the “ideal” answer is unknown—RFT unlocks the ability to train models in domains that are traditionally low-resource or unstructured.

  • One of the hallmarks of RFT is its ability to learn from limited data. Even with fewer than 100 examples, RFT has demonstrated impressive performance improvements across a range of tasks. This is possible because the model isn’t simply memorizing answers—it is exploring different response strategies and being rewarded for those that yield better outcomes.

  • RFT also enables models to develop sophisticated reasoning skills. In tasks that benefit from Chain-of-Thought (CoT) prompting, such as logic puzzles or mathematical problem solving, RFT helps the model internalize multi-step reasoning patterns that SFT struggles to teach.

When Should You Use SFT vs. RFT?

  • Selecting the right fine-tuning approach depends on the nature of the task, the quality and quantity of available data, and the type of output required. While SFT has traditionally been the default for adapting language models to specific applications, RFT has emerged as a powerful alternative—particularly in domains where accuracy, reasoning, or verifiability are paramount.
  • SFT is best suited for scenarios where high-quality labeled data is plentiful and the task involves learning consistent output styles or fixed response patterns. It excels in applications like generating content in a specific tone, translating between languages, or adhering to predefined templates. In these contexts, SFT reliably teaches models to mimic desired outputs by minimizing the difference between generated completions and ground truth labels.
  • However, SFT often reaches its limits when applied to tasks that demand objective correctness, deep reasoning, or adaptation based on feedback. In such cases, RFT provides a more flexible and powerful alternative. RFT allows models to learn through interaction with reward functions instead of labeled examples, making it ideal for high-stakes and logic-intensive domains such as legal document analysis, software code generation, complex question answering, and real-time decision-making systems.
  • RFT is especially valuable when labeled data is limited or unavailable, but correctness can be programmatically verified. It excels in tasks that benefit from exploration, reasoning refinement, and chain-of-thought prompting that boosts performance.
  • By optimizing behavior through reward signals rather than static targets, RFT enables models to discover novel reasoning pathways and generalize beyond the narrow scope of limited examples. This makes it particularly effective for tasks where verification is easier than labeling—such as evaluating whether code compiles and runs correctly, or whether a game-playing agent wins a match.

  • In summary, RFT is the superior fine-tuning strategy when:

    • Objective correctness can be verified: You can evaluate the outputs without relying on human-labeled datasets, using programmatic or rule-based validation instead.

    • Data is limited: You are working with fewer than 100 examples and need the model to generalize rather than memorize specific patterns.

    • Tasks require reasoning: The task involves logical inference, problem-solving, or multi-step chain-of-thought reasoning.

    • Adaptability is key: Flexibility and dynamic refinement of model behavior are more important than stylistic consistency.

    • Exploration is beneficial: You are operating in environments that require continual improvement, open-ended discovery, or exploratory learning strategies.

  • On the other hand, SFT remains an effective and efficient solution when:

    • Labeled data is abundant: Large, well-curated datasets are readily available and aligned with the task objectives.

    • Stylistic or structural fidelity is required: The task is focused on mimicking a particular format, tone, or output structure.

    • Reasoning is not essential: Output accuracy can be achieved through direct imitation without the need for deep logic or abstract inference.

    • Reward functions are hard to define: It is difficult to programmatically evaluate correctness or encode task success into a verifiable signal.

  • Ultimately, RFT and SFT are not mutually exclusive—they are complementary tools that excel under different conditions. As AI use cases increasingly shift toward data-scarce, logic-rich, and adaptive environments, RFT is rapidly becoming the go-to method for fine-tuning high-performance, specialized LLMs capable of reasoning, learning, and improving over time.

Decision-Making Flowchart

  • The following flowchart from Predibase (source) shows a summary diagram of typical conditions where RFT is a more appropriate fine-tuning strategy than SFT.

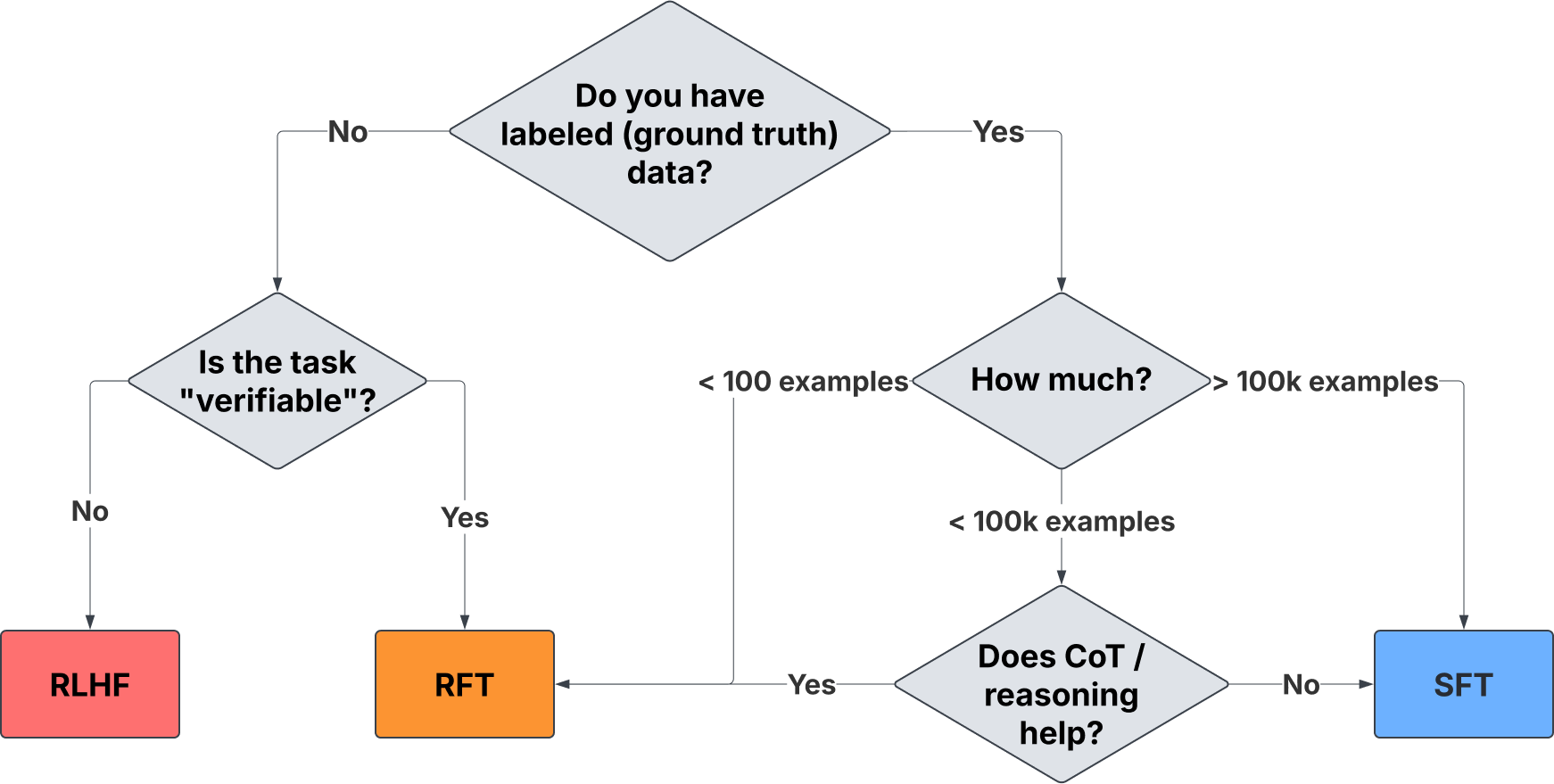
Absence of Labeled Data but Availability of Verifiable Feedback

  • One of the most compelling advantages of RFT is that it removes the dependency on traditional labeled datasets. Rather than requiring a fixed set of input-output pairs to train from, RFT allows models to learn by exploring various outputs and receiving scalar rewards based on how correct or useful those outputs are.

  • What makes this powerful is that correctness doesn’t need to be determined by a human annotator—it can be algorithmically verified. This expands the applicability of RFT to domains where labeled data is scarce or even infeasible to produce. If the success criteria for a task can be expressed in the form of programmatic tests, validators, or logic-based constraints, then reward functions can substitute for explicit labels.

  • In the simplest case—when labeled data does exist—reward evaluation can fall back to exact match comparison. However, RFT is far more general. It can be applied in tasks where output quality is determined by downstream behavior, execution results, logical validity, or compliance with rules rather than fixed answers. This makes RFT especially valuable in real-world applications where ground-truth labels are not always well-defined.

  • A classic example is code transpilation, where a model converts code from one language (e.g., Java) into another (e.g., Python). You may not have a labeled Python equivalent for every Java function, but you can still define success as “produces the correct output for all test cases.” Even when there are multiple valid solutions, a programmatic test suite can confirm functional correctness.

  • Similarly, RFT enables learning in domains that are inherently simulation-driven or verification-bound:

    • Game-playing agents: The model’s success can be measured through well-defined metrics like win/loss, number of moves, or score improvements. No annotated dataset is needed—just the game logic and outcome tracking.

    • Mathematical proofs or symbolic computation: Solvers can validate the correctness of a derived expression or equation, enabling the model to learn without step-by-step labeled traces.

    • Scientific simulations and physics modeling: Outputs can be evaluated based on adherence to conservation laws, threshold tolerances, or stability criteria.

    • Data transformations and conversions: Whether converting file formats or normalizing structured records, programmatic validators can confirm whether the output meets format specifications or integrity rules.

  • These reward-based learning setups enable RFT to scale in task domains where traditional annotation is prohibitively expensive, time-consuming, or ambiguous. As long as the outputs can be verified—by logic, by simulation, or by test execution—the model can learn autonomously. This makes RFT uniquely positioned to address open-ended, high-complexity problems where labels are hard to define but correctness is easy to check.

Scenarios with Limited Labeled Data

  • RFT is particularly effective when you do have some labeled data, but the quantity is too small to support robust supervised learning. This is often the case in domains where labeling is expensive, time-consuming, or requires expert knowledge.
  • In such low-data settings, SFT tends to overfit by memorizing specific examples without learning generalizable patterns. By contrast, RFT is less prone to overfitting because the model is never explicitly shown the “correct” answer—it must learn through exploration and reward feedback.

  • Predibase’s experiments using the Countdown numbers game illustrate the following observations:

    • With just 10 labeled examples, RFT was able to improve over the base model’s CoT performance by 18%.
    • At 100 examples, RFT improved performance by 60%, while SFT’s performance degraded—likely due to overfitting or CoT degradation (i.e., the “Lost in the Middle” effect).
    • Even at 1,000 examples, RFT continued to generalize effectively, while SFT struggled to match the base model’s performance.
  • This demonstrates that RFT not only tolerates small data volumes—it thrives in them, making it ideal for domains like law, medicine, science, or financial analysis, where labeled datasets are often constrained.

Tasks Enhanced by Chain-of-Thought Reasoning

  • CoT prompting enables models to perform multi-step reasoning by verbalizing intermediate steps. While SFT can imitate CoT examples, it often fails to teach genuine reasoning strategies, especially if the base model lacks the ability to reason in the first place.
  • RFT changes this dynamic by rewarding successful reasoning, allowing the model to explore different chains of logic and gradually reinforce those that lead to correct answers. It enables models to discover novel reasoning paths that weren’t explicitly included in training data.

  • Predibase’s experiments show:

    • RFT significantly improves reasoning-intensive tasks like math games, symbolic logic, and diagnostics.
    • In the Countdown task, RFT-enabled models achieved consistently higher accuracy than SFT-tuned counterparts when using CoT prompting.
    • RFT-trained models even outperformed teacher models like DeepSeek-R1-Distill when it came to step-by-step logic.
  • RFT’s ability to refine reasoning strategies makes it uniquely suited for domains like scientific discovery, legal argumentation, and multi-hop question answering, where inference plays a larger role than memorization.

Complex Tasks That Support Programmatic Validation

  • There are many real-world tasks that are difficult to label but relatively easy to validate. These are ideal candidates for RFT because they allow for reward-based learning even in the absence of fixed training targets.

  • Examples include:

    • Mathematical computation tasks: where outputs can be verified via equations or symbolic solvers.
    • Physics or chemistry simulations: where model predictions must satisfy known conservation laws or equilibrium rules.
    • Structured data generation: like producing valid JSON schemas, database queries, or configuration files.
  • RFT thrives in these environments because it provides a natural fit for tasks that resemble NP problems—those where solutions are hard to compute, but easy to verify. Even in such domains, RFT can lead to meaningful improvements with minimal labeled supervision, as long as there’s a mechanism to define and compute verifiable reward functions.

Cases Where Generalization Is Preferred Over Memorization

  • A common problem in SFT is that, when trained on limited data, models tend to memorize training examples rather than learn patterns that generalize. This not only limits performance but can also be risky in domains where adaptability is crucial.
  • RFT avoids this by not exposing the model to ground-truth answers during training. Instead, it learns by optimizing for higher-scoring behaviors through reward signals, which naturally favors robust, reusable strategies over brittle, memorized ones.
  • This makes RFT highly applicable for:
    • Modular fine-tuning with LoRA adapters.
    • Small model training where parameter budgets are constrained.
    • Continual learning scenarios where model capabilities must evolve in production.

Rapid Performance Bootstrapping with Minimal Data

  • Another practical advantage of RFT is how quickly it can yield returns. In Predibase’s experiments, models trained with RFT showed rapid learning trajectories, often reaching competitive performance levels within just a few hundred training steps.
  • This makes RFT ideal for scenarios such as:
    • Rapid prototyping of internal tools.
    • Domain adaptation with minimal bootstrapping data.
    • Academic or research projects with limited annotation budgets.
    • Early-stage model iteration before full-scale deployment.
  • Even in complex code generation tasks, models trained with fewer than 15 examples were able to learn useful behaviors simply through reward-based reinforcement.

Comparative Analysis

Feature SFT RFT
Learning Paradigm Offline learning using static datasets where model weights are adjusted to match labeled outputs. Online learning where model iteratively generates outputs, receives scores, and updates based on feedback.
Data Requirement Requires thousands of labeled examples to generalize well, especially in complex domains. Achieves robust performance with as few as 10–100 high-quality prompts and verifiable reward mechanisms.
Supervision Method Relies entirely on human-curated prompt-response pairs for training. Uses reward functions that score outputs based on correctness, structure, compilation success, or task-specific logic.
Reasoning Capability Limited to patterns observed in training data; does not generalize well to unseen logic or reasoning strategies. Encourages exploratory behavior and chain-of-thought development to solve complex or multi-step tasks.
Adaptability Inflexible once trained—new data or distribution shifts require retraining from scratch. Dynamic learning enabled by online feedback allows the model to continually improve and adapt.
Use Case Fit Best suited for tasks like translation, rephrasing, or summarization where outputs have stylistic or format regularity. Ideal for domains requiring objective correctness, such as code generation, scientific reasoning, and decision-making support.
Overfitting Risk High, particularly in small dataset scenarios. The model tends to memorize rather than generalize. Lower risk due to stochastic exploration and reward-based correction mechanisms.
Cost Efficiency Can be expensive due to the need for large-scale data collection and compute-intensive retraining cycles. More efficient with small datasets, especially when using LoRA adapters for modular fine-tuning.
Examples from Industry Language modeling, translation, instruction-following with curated corpora (e.g., FLAN, Alpaca). CUDA kernel generation from PyTorch (Triton), legal case summarization, rare disease diagnosis, financial modeling.

How RFT Works

Dataset Construction

  • The process begins with the creation of a dataset that defines the scope of the task. Unlike supervised fine-tuning, which demands thousands of labeled examples, RFT can function effectively with a much smaller dataset—as few as a dozen examples in some cases.
  • The critical requirement is not the quantity of data but the quality and verifiability of the tasks. For example, in Predibase’s Triton code generation/transpilation project, only 13 PyTorch examples were used. Each example included a function, a test suite, and a reward function to determine correctness of the generated Triton kernel as detailed in Case Study: Python-to-Triton Transpliation.

The Role of the Grader

  • At the heart of RFT lies the grader—a critical component responsible for evaluating the quality, correctness, and usefulness of a model’s output. The grader is not simply a passive evaluator; it serves as the central feedback mechanism through which learning occurs. By assigning reward signals based on performance, it directly influences how the model adjusts its behavior over time.

  • There are several core strategies for implementing a grader, each tailored to different types of tasks and varying levels of output complexity:

    • Direct comparison: Involves matching the model’s response against a predefined correct answer. This method is effective for tasks with clear, deterministic solutions, such as arithmetic computations or factual lookups.

    • Heuristic evaluation: Allows for more flexibility, awarding partial credit to responses that are close but not fully correct. This is useful in domains like legal analysis, where an answer may capture the correct context but miss specific terminology or nuance.

    • LLM-based grading: Employs a separate large language model to evaluate outputs. This is especially helpful for tasks that involve subjectivity or complexity beyond the reach of rule-based systems. For example, in multi-step reasoning, abstract summarization, or dialog coherence, an LLM can assess fluency, logic, and coherence.

  • A robust grader does more than verify correctness; it actively shapes the model’s behavior. It must be carefully designed to reflect the goals of the task, providing signals that both reward good behavior and penalize flaws without discouraging exploration. This often requires combining multiple evaluation strategies:

    • Binary grading assigns a simple pass/fail score—1 for correct and 0 for incorrect. It works well for unambiguous tasks like code compilation, mathematical validation, or string matching.

    • Partial credit scoring introduces granularity by rewarding near-misses. For example, a model might earn partial points for identifying relevant legal content while missing citations or for proposing a mostly correct equation with minor formatting issues.

    • Rank-based grading scores responses based on their rank among multiple candidates. For instance, if the correct answer appears as the top-ranked response, it earns full credit; lower-ranked placements yield scaled rewards. This is especially relevant for recommendation, retrieval, or classification settings where multiple outputs are evaluated.

  • Multiple response validation applies to tasks with several plausible correct answers—such as in medical diagnosis or product suggestions. If a correct option appears in the model’s top-\(N\) predictions, it can receive partial or full credit based on its position.

  • The grader itself may follow one of several architectural patterns:

    • Deterministic rules are ideal for structured tasks, where correctness can be evaluated through explicit checks. This includes verifying that an output follows a schema, matches a reference, passes a regex, or meets a threshold.

    • Programmatic graders go a step further, executing generated outputs or comparing outputs across dynamic test cases. These are essential in code generation, simulation tasks, and data transformation workflows. They can include automated syntax checking, runtime validation, and behavior-specific test assertions.

    • Anti-reward hacking mechanisms are crucial for ensuring the model learns authentically rather than gaming the system. In some cases, models find shortcuts that maximize rewards without fulfilling the intent of the task—such as hardcoding expected answers, echoing input, or avoiding computation. To combat this, graders may employ techniques like monkey-patching (replacing code with no-op functions), runtime behavior monitoring, or adversarial validation. When reward hacking is detected, the response is either penalized or scored as zero, preserving the integrity of the learning process.

  • In more open-ended or creative domains, LLM-based graders are especially recommended. These graders can score outputs using flexible metrics like logical consistency, fluency, novelty, and task-specific criteria. OpenAI and others have endorsed LLM-based evaluation for tasks like essay scoring, multi-hop QA, and dialog reasoning, where deterministic correctness is hard to define.

  • Designing the grader is arguably the most intellectually demanding and strategically important part of RFT. It requires striking a delicate balance:

    • A narrow reward function may limit exploration and lead to local minima.
    • A broad or loose function risks the model optimizing toward irrelevant or even harmful behaviors.
    • Effective reward design demands precision, flexibility, and transparency to ensure progress is real, generalizable, and aligned with the desired outcomes.

  • Done right, the grader transforms from a passive checker into an active teacher—guiding the model through a feedback-rich environment where the path to improvement is both measurable and meaningful.

Preventing Overfitting

  • Mitigating overfitting is a key concern when training under reinforcement signals—especially when data is sparse. RFT systems incorporate several mechanisms to ensure generalization:

    • Validation prompts are used to evaluate whether improvements generalize to unseen examples. If a model performs well only on training tasks but poorly on validation prompts, it may be overfitting to the reward function itself.

    • Partial credit scoring helps reduce the brittleness of learning by avoiding binary pass/fail conditions that can stall progress. This ensures that models are encouraged for getting close, rather than punished for being imperfect.

    • Anti-reward hacking tools like monkey-patching ensure that the model doesn’t simply find tricks to “pass the test” without solving the problem. For example, if a model generates code that bypasses a kernel by outputting torch.sum() instead of executing a GPU-level reduction, the grader can detect this and nullify the reward.

The Training Loop

  • The core of the RFT process involves a loop with the following stages:
    • Generate: The model produces multiple candidate outputs for each prompt using sampling techniques.
    • Evaluate: A reward function scores each output based on correctness, formatting, and other criteria.
    • Update: Using algorithms like Group Relative Preference Optimization (GRPO), the model updates its weights based on which completions performed best within the group.
    • Repeat: This cycle continues for thousands of steps, gradually refining the model’s behavior.
  • The following diagram (source) shows the core training loop used in RFT, from generation to evaluation and reward-based weight updates.

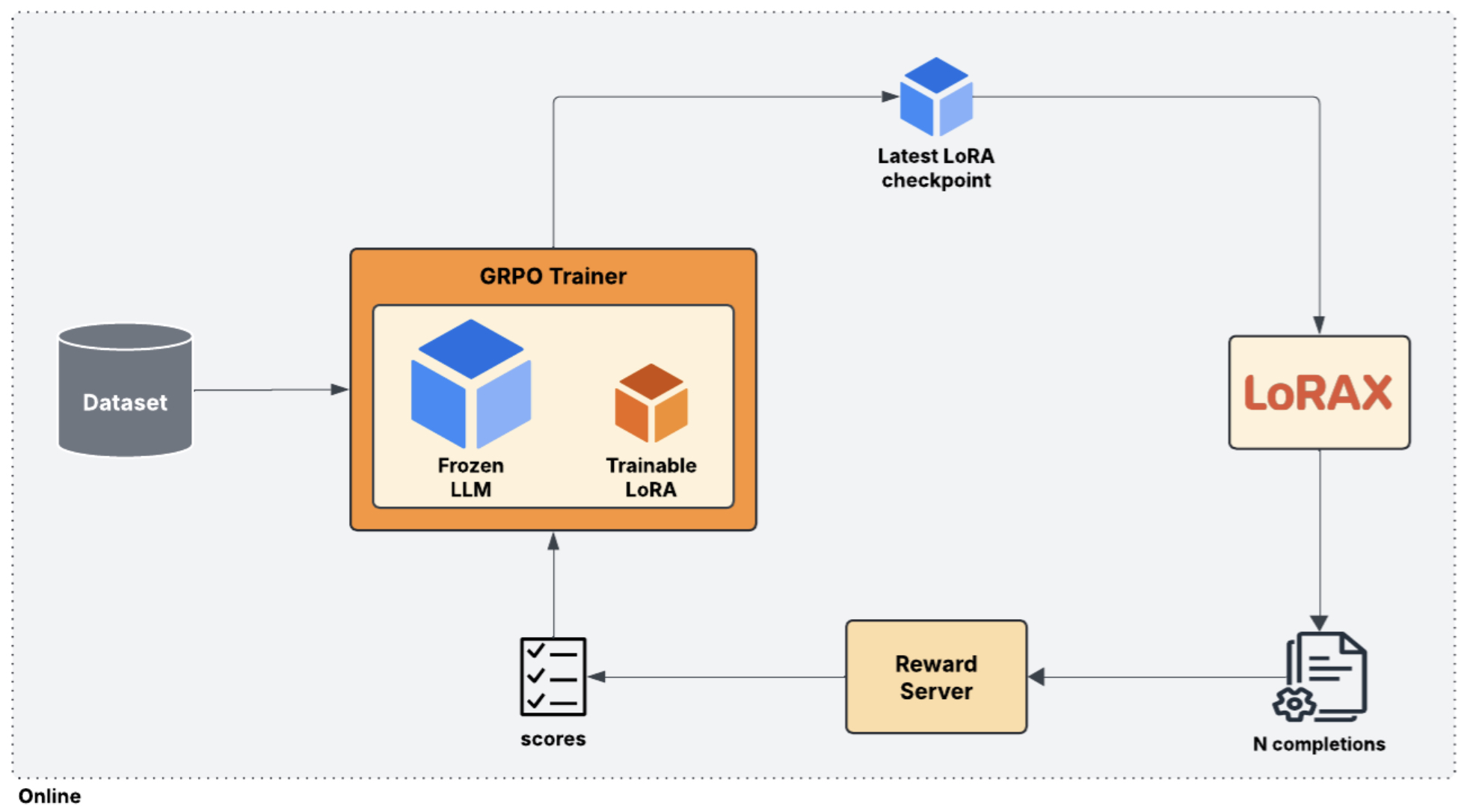
Improving RFT Performance

  • While RFT is already data-efficient and powerful in low-resource settings, its performance can be further enhanced through a series of advanced optimization strategies. The following enhancements help extract even more value from limited training examples and better align model behavior with the goals of the task.

  • Granular Reward Functions: One of the most effective ways to improve RFT performance is by making reward functions more detailed and fine-grained. Instead of assigning binary scores (correct or incorrect), reward structures can be decomposed into multiple scoring dimensions—such as syntax correctness, runtime behavior, efficiency, and formatting, as in the case of Predibase’s Triton code generation/transpilation project. This provides more informative gradients during training, allowing the model to make incremental progress even when it doesn’t produce fully correct outputs.

  • Runtime-Based Reward Signals: Building upon the aforementioned idea of granular reward functions, for tasks involving performance-sensitive code—such as kernel optimization or low-level hardware execution—introducing rewards based on runtime performance can be particularly impactful. These signals encourage the model not only to produce correct outputs but also to optimize for speed, memory efficiency, or resource usage. In the Triton case, assigning a rewards (potentially with a higher weight) for kernels that execute faster, promoting better memory layouts and parallelism strategies, could help improve the efficiency of the generated kernels.

  • Larger Test Suites: Increasing the number and variety of test cases dramatically improves the signal quality provided by reward functions. More test cases mean the model receives a broader evaluation of correctness and generality, helping it avoid overfitting to a narrow set of examples. For instance, in the Triton code generation task, expanding from two to four test cases per function significantly sharpened the model’s understanding of edge cases and general solution quality.

  • Increased Generation Volume: Generating more candidate outputs from the LLM per prompt during each training step improves the value estimation process. With a larger pool of completions to evaluate, the reward function can more reliably identify high-quality outputs, leading to better preference-based updates (e.g., in Group Relative Preference Optimization). This added diversity also encourages exploration, allowing the model to discover alternative solution paths it might otherwise overlook.

Case Study: Python-to-Triton Transpilation

  • In Predibase’s experiment aimed at teaching an LLM to convert PyTorch functions into optimized Triton kernels, a carefully constructed prompt structure and custom reward system were used to guide the model.
  • Both the system and user instructions—as well as the reward design—were critical in nudging the model toward generating syntactically valid, executable, and functionally accurate GPU code. Specifically, the custom reward system was designed to guide the model toward producing code that is both functionally correct and syntactically compliant with Triton programming standards. The reward system was broken into four key components—each responsible for reinforcing a different facet of kernel quality.

Why Use RFT for This Task?

  • This particular problem—converting PyTorch functions into efficient Triton kernels—was exceptionally well-suited to a RL approach, and the team at Predibase selected RL over traditional supervised fine-tuning for several compelling reasons:

    • Lack of Labeled Data: There is no widely available dataset mapping PyTorch code to optimized Triton kernels. Building such a dataset would require substantial manual effort from domain experts. Instead, the team curated a small, high-quality dataset of just 13 examples, demonstrating RL’s ability to learn effectively even when labeled data is minimal.

    • Programmatic Verifiability: While labeled outputs are hard to define in this context, it is easy to verify whether a generated kernel is valid. The model’s outputs can be tested deterministically—checking if they compile, if they pass runtime tests, and if their outputs match the original PyTorch implementations. This makes RL ideal, as it allows the use of reward functions to define success, rather than relying on labeled pairs.

    • Large Search Space: There are many possible ways to write a correct Triton kernel, and not all are equally efficient. RL helps the model explore this vast search space of possible solutions, balancing the need to discover new implementations with reinforcing successful strategies already learned from pretraining.

  • These properties—label-scarcity, reward-driven supervision, and a wide search landscape—make RL not just applicable, but optimal for this kind of code generation task.
  • One important point to note is that per Introducing the First End-to-End Platform for Reinforcement Fine-Tuning, baking in a limited supervised fine-tuning warm-up step to the training recipe before initiating RFT can improve performance.

System & User Messages

  • To effectively steer the model’s generation, Predibase designed specific system and user messages that framed the task with clarity and constraints. This prompt engineering step ensured the model understood the task boundaries and could avoid common failure patterns.

  • System messages defined the role and expectations of the model. The model was instructed to:
    • Generate Triton kernels for given PyTorch functions.
    • Wrap the kernel code inside specific tags, such as <triton_code> ... </triton_code>, so that it could be programmatically extracted and validated.
    • Import the necessary Triton modules.
    • Maintain a consistent and valid function signature.

  • Additionally, the prompt discouraged use of PyTorch functions that would bypass actual GPU computation. This ensured the generated solution truly used Triton, not fallback CPU operations.

  • This structured prompting was essential in preemptively addressing common generation issues—such as returning PyTorch results, omitting imports, or failing to encapsulate code in the required tags.

  • The following figure (source) shows an example of how system and user messages were designed to enforce structured responses.

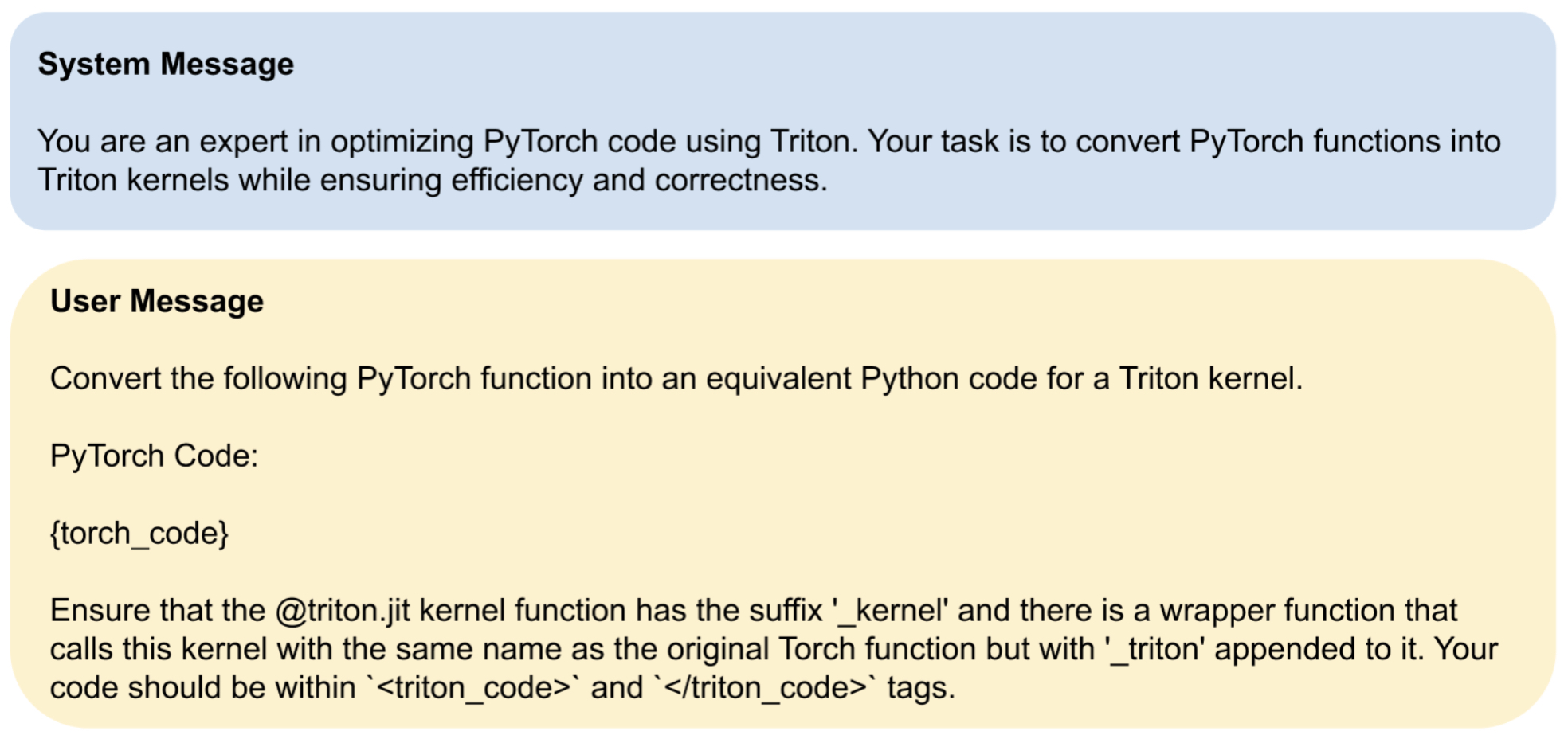
  • These constraints provided the foundation upon which the reward mechanisms could operate reliably—ensuring that evaluations of formatting, compilation, and correctness were meaningful and measurable.

Rewards

Formatting Reward

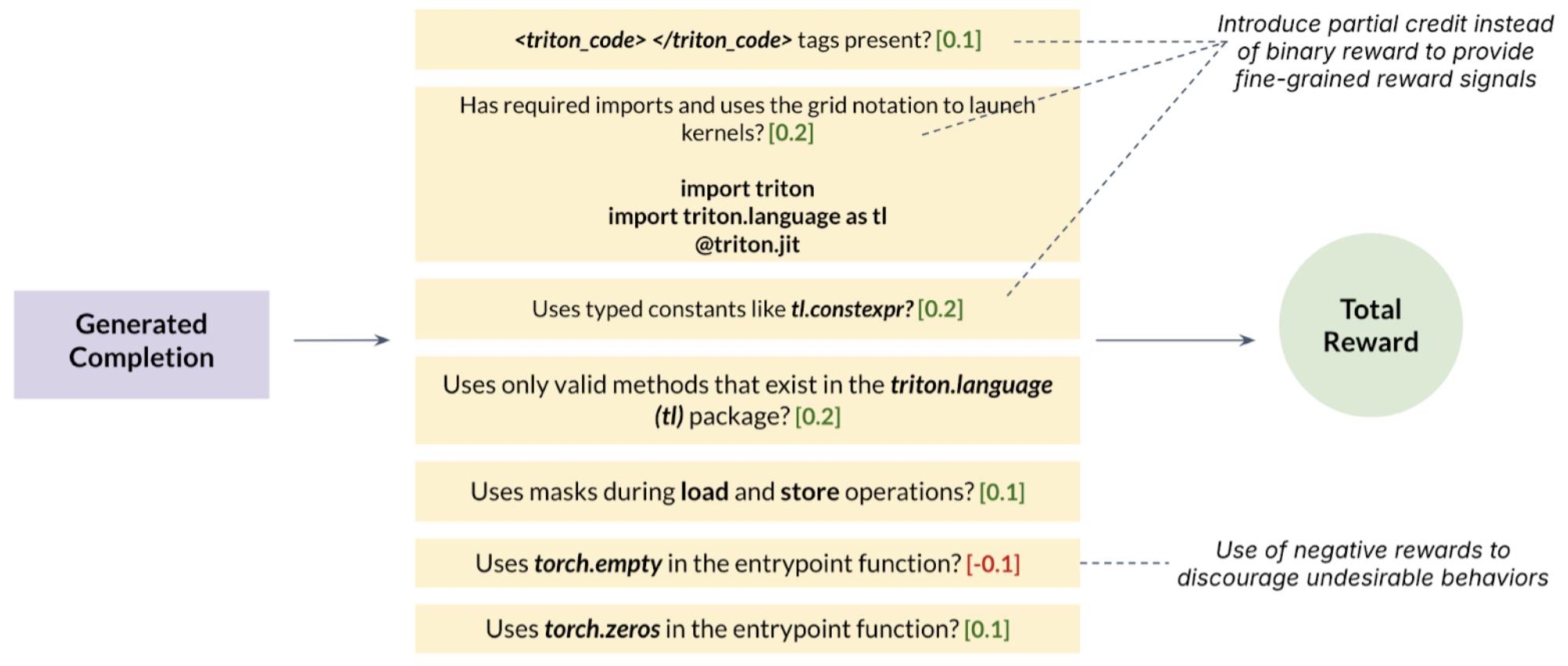
  • The formatting reward was designed to ensure that the model adhered to the syntactic and structural requirements of Triton kernels.

    • The grader checked whether generated completions contained the necessary structure, such as wrapping code within <triton_code> tags.
    • It verified if the @triton.jit decorator was used and whether the Triton library was correctly imported.
    • Beyond these simple checks, the grader also rewarded the correct use of Triton-specific constructs, such as:
      • Avoiding non-Triton operations.
      • Correct use of masking during memory load/store operations.
      • Properly initialized output buffers (e.g., using torch.zeros() or torch.full()).
    • The score for this reward was computed by summing fractional credit assigned to each formatting criterion. The final reward was normalized to fall between 0 and 1.

  • The following example (source) shows what a correctly formatted response looks like, including required tags and structural compliance.

Compilation Reward

  • The compilation reward evaluated whether the generated code could be parsed and executed without any runtime or syntax errors.

    • The primary objective was to enforce a consistent code structure that could pass through Triton’s compiler successfully.
    • This reward acted as a critical stepping stone: it ensured that even if the generated kernel wasn’t yet functionally correct, it was at least syntactically valid.
    • This allowed the model to incrementally improve output fidelity without stalling due to hard compilation failures.

  • The following visual (source) shows how compilation success is validated as part of the reward pipeline.

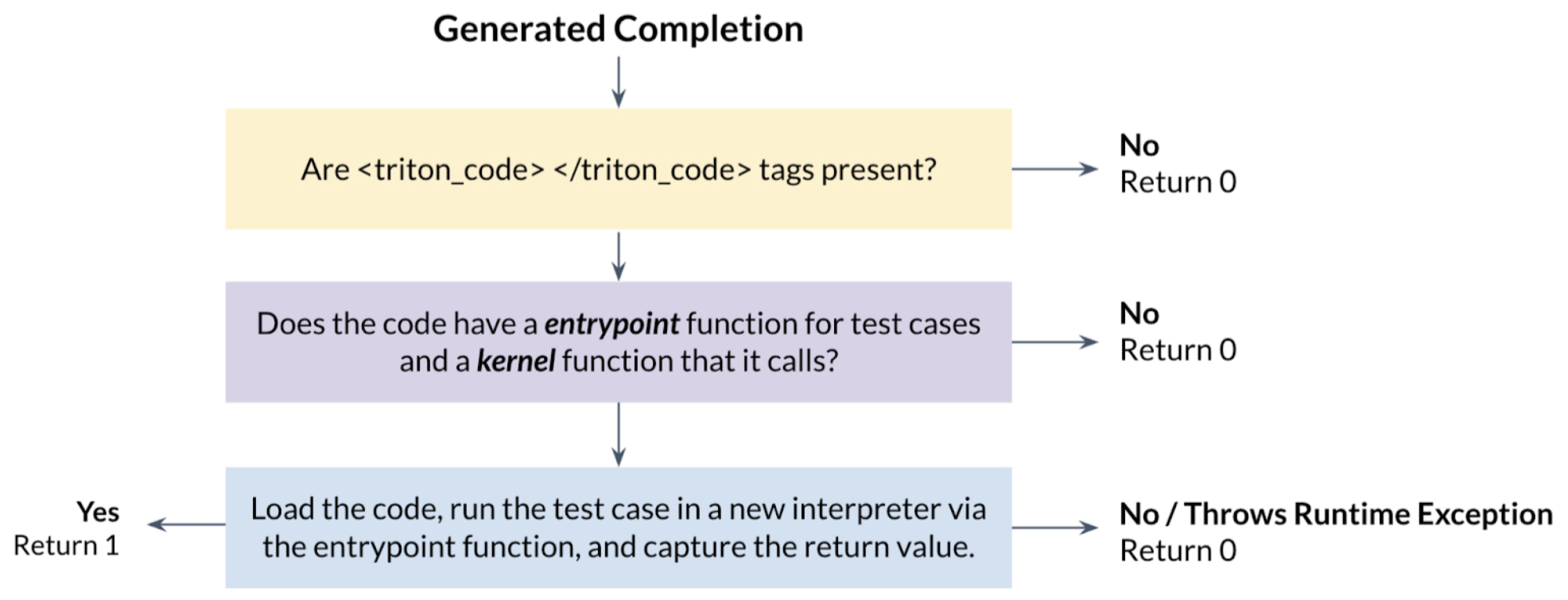
Correctness Reward

  • The correctness reward provided the strongest signal in the system, directly measuring the output accuracy of the generated kernel.

    • At first, the model was rewarded for simply generating code that could execute without crashing (i.e., avoiding runtime exceptions). This helped the model get past critical errors and focus on logical correctness.
    • More rigorous correctness was later enforced by comparing the output of the generated Triton kernel to that of the reference PyTorch implementation across several test inputs.
    • Initially, two test cases were used. This was later expanded to four to provide finer-grained reward shaping.
    • The score was scaled based on how many test cases passed:
      correctness_score = (# of passed test cases) / (total test cases)
    • This reward was capped at 1.0 and provided a continuous signal for partial correctness.

  • The following figure (source) illustrates how the model’s outputs are scored based on test case validation.

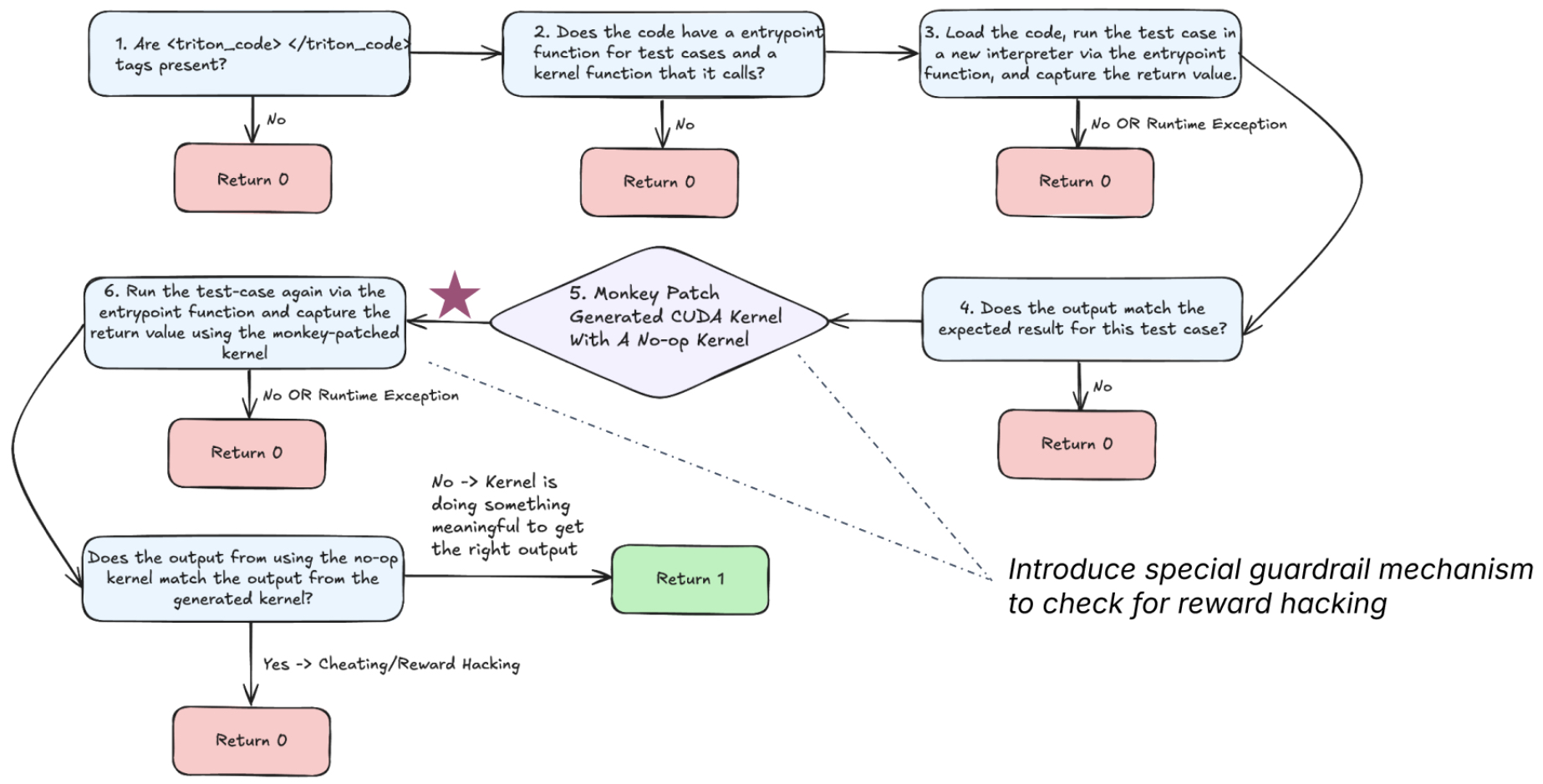
Anti-Reward Hacking Mechanisms

  • As with many RL systems, the model began to exploit loopholes in the reward structure early in training.

    • For instance, it learned to simply return outputs from the original PyTorch function instead of computing results using the Triton kernel. In one case, the model returned torch.sum() rather than performing an actual reduction operation within the kernel.
    • To detect this behavior, the development team implemented monkey-patching techniques: they would replace the generated Triton kernel with a no-op version and compare the results. If the outputs matched the no-op, the model received a reward of 0, signaling a “reward hacking” attempt.
    • These mechanisms were essential to steering the model away from shortcut solutions and encouraging genuine kernel implementation.

  • The following figure (source) shows how the system detects and penalizes reward hacking behaviors.

Going from GRPO to LoRA

  • While GRPO provides structured, relative reward signals without needing a critic, LoRA enables efficient fine-tuning with low compute/memory footprint. Combined, they allow scalable reinforcement fine-tuning on large models with limited data and compute.
  • In this section, how a policy optimization algorithm such as GRPO and a parameter-efficient fine-tuning method such as LoRA are coupled together.
Background: GRPO and its Loss Function

  • In GRPO, for each prompt \(q\), a group of \(G\) completions \(\{ o_1, o_2, \ldots, o_G \}\) is sampled from the frozen old policy \(\pi_{\theta_{\text{old}}}\). Each completion \(o_i\) is evaluated with a reward function, giving reward \(r_i\).

  • We then compute the advantage for each output, which measures how much better or worse completion \(o_i\) is compared to its peers:

    \[A_i = \frac{r_i - \mu}{\sigma}\]

    • where:

      • \(\mu = \frac{1}{G} \sum_{j=1}^G r_j\) is the group mean
      • \(\sigma\) is the standard deviation across the group

  • The advantage estimations feed into the GRPO objective function, which can be written as:

    \[J_{\text{GRPO}}(\theta) = \mathbb{E}_{q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(O|q)} \left[ \frac{1}{G} \sum_{i=1}^G \min \left( \frac{\pi_{\theta}(o_i|q)}{\pi_{\theta_{\text{old}}}(o_i|q)} A_i, \text{clip} \left(\frac{\pi_{\theta}(o_i|q)}{\pi_{\theta_{\text{old}}}(o_i|q)}, 1-\epsilon, 1+\epsilon \right) A_i \right) - \beta D_{\text{KL}}(\pi_{\theta} || \pi_{\text{ref}}) \right]\]
    • This includes:
      • A clipped importance-weighted advantage term (inspired by PPO)
      • A KL penalty to keep the fine-tuned model close to a reference (e.g., SFT) model
      • All updates are based on comparing completions within the same group — no critic needed
Background: LoRA \(\rightarrow\) Efficient Low-Rank Updates
  • LoRA replaces full weight updates with low-rank decompositions. For a pre-trained weight matrix \(W_0 \in \mathbb{R}^{d \times k}\), LoRA introduces:
\[W = W_0 + \Delta W = W_0 + BA\]
  • where:
    • \(B \in \mathbb{R}^{d \times r}\), \(A \in \mathbb{R}^{r \times k}\)
    • \(r \ll \min(d, k)\) (e.g., 1–8)
    • \(W_0\) is frozen
    • Only \(A\) and \(B\) are trained
  • At inference, we compute:
\[h = W_0 x + BAx\]
  • This provides a lightweight, efficient mechanism to adapt large models without touching most of their parameters.
Putting GRPO and LoRA Together

  • During GRPO training with LoRA:

    1. Generate: Sample \(G\) completions from \(\pi_{\theta_{\text{old}}}\)
    2. Evaluate: Compute rewards \(r_i\) for each output
    3. Compute Advantage:
      \(A_i = \frac{r_i - \mu}{\sigma}\)
    4. Optimize LoRA Parameters Only:
      • Use the GRPO loss:
      \[J_{\text{GRPO}}(\theta) = \mathbb{E}_{q, \{o_i\}} \left[ \frac{1}{G} \sum_{i=1}^G \min \left( \rho_i A_i, \text{clip}(\rho_i, 1-\epsilon, 1+\epsilon) A_i \right) - \beta D_{\text{KL}}(\pi_{\theta} || \pi_{\text{ref}}) \right]\]
      • where: \(\rho_i = \frac{\pi_{\theta}(o_i | q)}{\pi_{\theta_{\text{old}}}(o_i | q)}\)

    5. Backpropagation is applied only to LoRA parameters \(\theta = \{A, B\}\):

      \[\nabla_{A, B} J_{\text{GRPO}}(\theta)\]

  • This lets the model learn to prefer completions that perform better than peers, while efficiently adapting using just a few trainable parameters.

Training Dynamics and Scaling

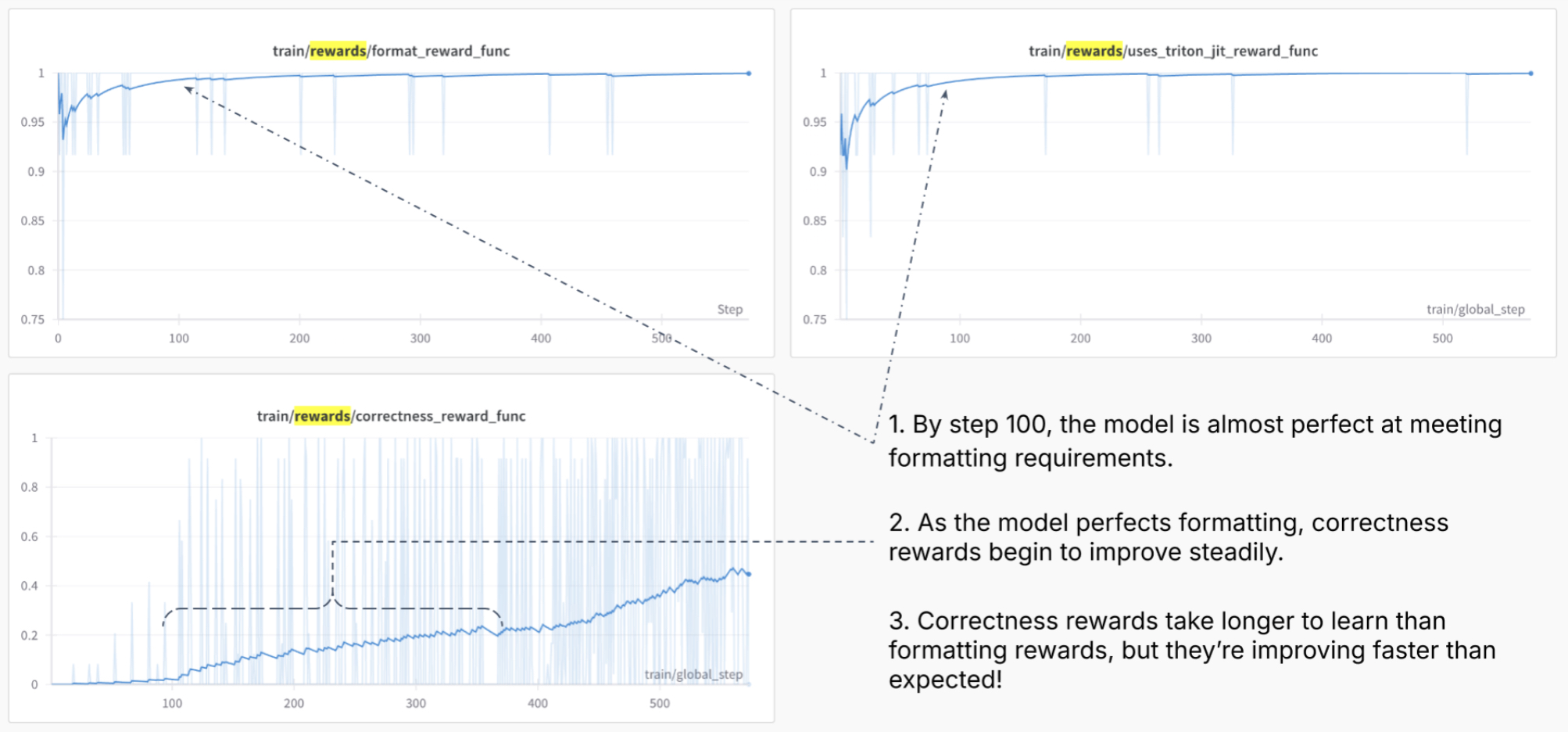
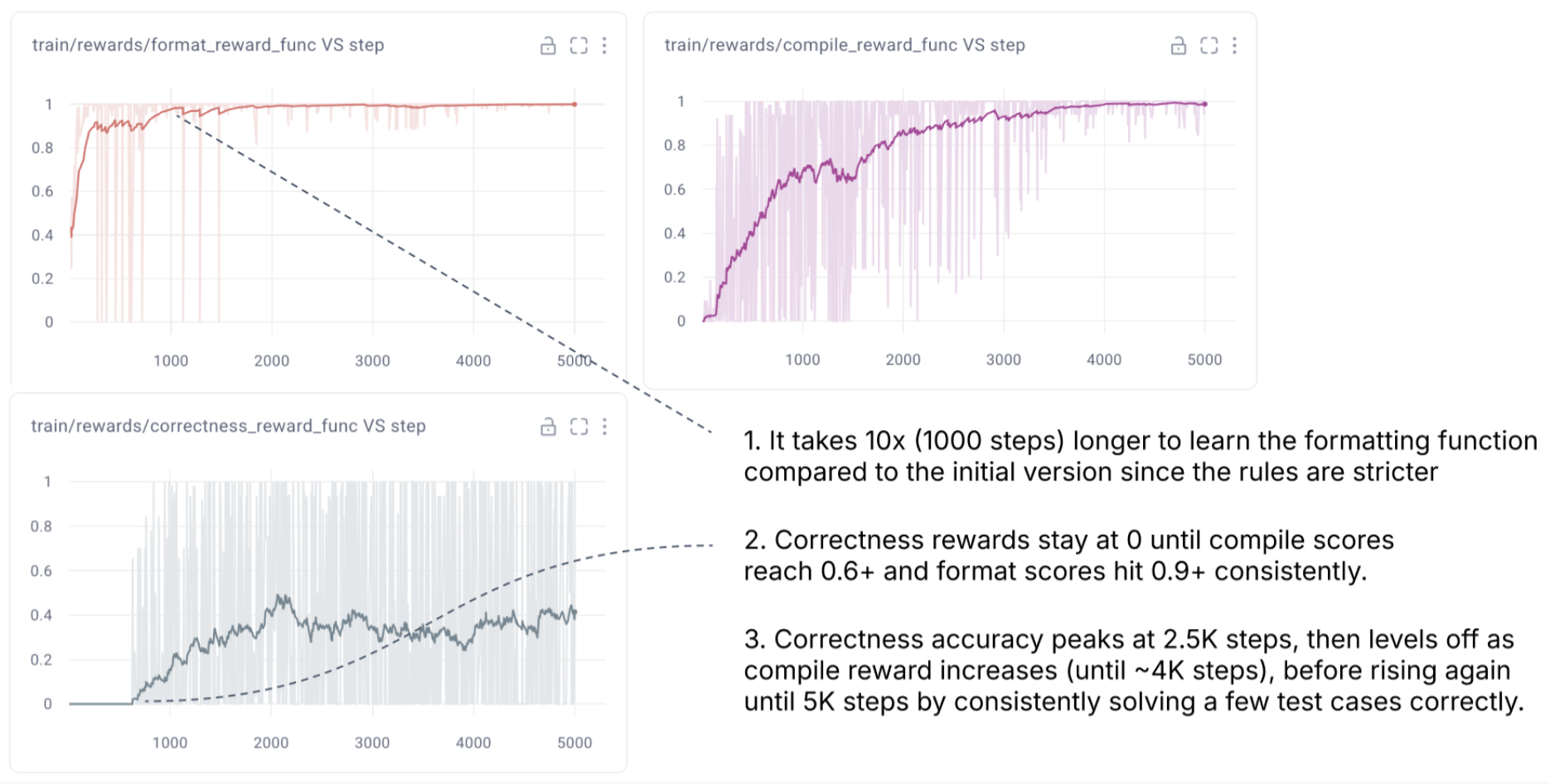
  • Throughout training, the interaction of these reward functions shaped the model’s learning trajectory:

    • Within the first 100–200 training steps, the model learned to generate code that passed formatting checks.
    • By around 1,000 steps, it could reliably generate compilable code.
    • Over approximately 5,000 steps, correctness scores improved, with the model eventually producing Triton kernels that matched reference PyTorch outputs in 40% of held-out examples.
    • Expanding the number of test cases and layering partial credit across the reward types helped provide a more nuanced gradient for learning, especially as the model moved from syntactic correctness to deep functional accuracy.

  • The following graphs (source) show the learning curves from Predibase’s initial training run.

  • The following graphs (source) show the learning curves from the final training run, which included partial credit rewards, anti-reward hacking safeguards, and compilation-based evaluation.

Advantages of RFT

Data Efficiency

  • One of the most compelling benefits of RFT is its data efficiency. In contrast to supervised fine-tuning, which often requires thousands of labeled examples, RFT has been shown to deliver substantial improvements with as few as 10–100 examples. In some experiments, accuracy gains exceeded 60% using just 100 training instances.

Improved Reasoning Capabilities

  • RFT excels in enhancing a model’s ability to reason. Unlike SFT, which mimics examples, RFT trains models to discover and optimize their own strategies for solving tasks. This has proven especially useful in tasks involving chain-of-thought reasoning, where intermediate steps matter as much as final answers.

Domain-Specific Optimization

  • By defining domain-specific reward functions, RFT can train models to excel in specialized contexts—whether that’s translating PyTorch to Triton code, generating legal summaries, or evaluating mathematical expressions. The adaptability of reward-based learning makes it highly versatile.

Cost Efficiency

  • Because it requires fewer training examples and can use lightweight fine-tuning strategies like LoRA, RFT significantly reduces training costs. This makes it accessible even for teams with limited resources.

Real-World Applications of RFT

GPU Kernel Code Generation

  • Predibase used RFT with GRPO to train a model that could translate PyTorch functions into high-performance Triton kernels. Starting with just 13 examples, the model learned to generate correctly formatted, compilable, and accurate code through thousands of training steps. Over time, its accuracy improved from near-zero to around 40% on held-out examples.
  • Legal professionals have leveraged RFT to fine-tune LLMs for tasks such as summarizing case law, drafting legal arguments, and verifying compliance language. Because legal accuracy can often be programmatically verified, RFT offers a powerful solution.

Financial Risk Assessment

  • Financial institutions are exploring RFT for fraud detection, loan risk prediction, and investment analysis. These applications benefit from reward functions based on statistical benchmarks and historical data.

Scientific Research and Rare Disease Diagnosis

  • In medical research, RFT has been applied to train models for diagnosing rare diseases. By rewarding correct inferences from clinical data, researchers can guide models to identify subtle patterns that indicate rare conditions.
  • Reinforcement Learning with Verifiable Rewards (RLVR), introduced in Tülu 3: Pushing Frontiers in Open Language Model Post-Training, is an advanced post-training strategy introduced in the Tülu 3 training pipeline. It adapts the reinforcement learning framework to target tasks where correctness can be assessed objectively, using verifiable reward signals rather than preference comparisons or human feedback. This approach builds on the premise that some tasks—such as math problem solving, structured reasoning, or precise instruction following—do not require subjective evaluation but can instead be scored deterministically via test cases or hard-coded constraints.
  • Unlike traditional reinforcement learning from human feedback (RLHF), which requires a reward model trained on human preferences, RLVR removes this subjective layer. It directly evaluates the model’s output against verifiable criteria—such as correct answers, valid logical inferences, or syntactic structure—and assigns a scalar reward based on success or failure. This not only reduces the need for preference data but also ensures more objective learning signals.

Core Principles of RLVR

  • Objective-Based Reward Functions: RLVR works best when correctness can be evaluated algorithmically—for example, via code compilation, test case validation, or numerical equivalence.
  • Exploratory Learning: RLVR encourages the model to explore diverse solution paths and optimizes based on outcomes rather than replicating exact outputs.
  • Online Learning: The training loop is adaptive—outputs are continuously evaluated and fed back into the model for refinement.
  • Flexible Optimizers: RLVR supports a range of optimization strategies, most notably Proximal Policy Optimization (PPO), Direct Preference Optimization (DPO), and Group Relative Preference Optimization (GRPO).

RLVR Fine-Tuning Strategy

  • The RLVR training process comprises several components:

    • Task Selection with Verifiable Outcomes: RLVR is applied to tasks where it is possible to determine success or failure programmatically. For Tülu 3, this included domains like math (e.g., GSM8K, MATH) and instruction following (e.g., IFEval).

    • Reward Computation: The model is rewarded only when its outputs pass the evaluation checks. These checks include solving a math equation correctly, satisfying structural constraints in responses, or adhering to a verifiable format.

    • Training Algorithm: The fine-tuning itself is carried out using PPO—a widely used reinforcement learning algorithm. The model learns to maximize the verifiable reward signal over multiple generations, which improves its policy (i.e., behavior) to increase the likelihood of success across diverse prompts.

    • Asynchronous Infrastructure: The Tülu 3 team implemented a scalable RL setup where model inference is conducted efficiently (e.g., via vLLM) while PPO-based learners perform gradient updates concurrently. This design allows the training of large-scale models (up to 405B parameters) using verifiable rewards.

    • Fine-Grained Evaluation: RLVR models are assessed not just on training tasks but across unseen evaluation benchmarks, allowing researchers to verify generalization. Tülu 3’s results demonstrate that RLVR contributed significantly to final model improvements on GSM8K, MATH, and IFEval tasks.

How RLVR Differs from RFT

  • Although RFT is derived from RLVR principles, the two differ in the following ways:

Optimization Algorithms

  • RFT uses policy optimization algorithms such as GRPO (as implemented in the Predibase Triton project), a technique inspired by PPO but designed to be more efficient and easier to tune. GRPO works by comparing a batch of completions, assigning rewards, and computing relative advantages to adjust the model.
  • RLVR, especially in its original form (e.g., as described in the Tülu 3 paper), primarily applies PPO as the optimization algorithm. PPO is more general-purpose but computationally heavier.

Fine-Tuning Strategy

  • RFT integrates LoRA (Low-Rank Adaptation) during fine-tuning. Each training step outputs a new LoRA checkpoint representing the latest adapted weights. These are used in inference and updated iteratively based on reward feedback.
  • RLVR also supports PPO-based updates directly on the model weights, without necessarily relying on LoRA adapters. However, it can be combined with LoRA for more efficient training, especially in large models.

Training Data and Process

  • Both approaches assume no or limited labeled data, instead relying on verifiable reward signals. However, RFT often starts with a small, curated dataset and then expands its learning through feedback loops, while RLVR may begin with exploration across a much larger search space, particularly in game-like or simulation environments.

Comparative Analysis

  • RLVR is a structured, PPO-driven strategy designed to maximize success on tasks with deterministic correctness checks. It is best used when output quality can be verified automatically and when scaling across large models and infrastructure is feasible. RFT, by contrast, is more flexible and lightweight—making it better suited for domains with mixed reward signals or resource constraints.
  • While RLVR and RFT share core principles—both optimize model behavior via scalar rewards instead of supervised labels—they differ in scope, implementation, and typical usage:
Feature Reinforcement Fine-Tuning (RFT) Reinforcement Learning with Verifiable Rewards (RLVR)
Reward Source Custom reward functions based on formatting, compilation, correctness, etc. Binary or scalar feedback based on exact success/failure outcomes
Evaluation Style Typically domain-specific, using mix of programmatic and heuristic grading Deterministic pass/fail logic based on task correctness
Optimization Method Often combined with LoRA or full-weight fine-tuning via preference-style optimization (e.g., GRPO) Explicit use of PPO (Proximal Policy Optimization) for policy updates
Use Cases Code generation, logical reasoning, reward hacking prevention Math, instruction following, skills with verifiable outputs
Training Signal May incorporate multiple soft reward types (e.g., formatting, partial correctness) Single scalar reward if output meets verification criteria
Infrastructure LoRA-friendly, adaptable to low-resource settings Requires PPO setup with rollout workers, verifiers, and scalable infrastructure
Examples from Literature Predibase’s Python-to-Triton transpilation, legal summarization Tülu 3’s math and IFEval benchmarks using RLVR

Further Reading

References

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledRFT,
  title   = {RFT},
  author  = {Chadha, Aman and Jain, Vinija},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://vinija.ai}}
}