Background

  • This article covers model inference/training optimization or compression concepts using topics such as model quantization/binarization, pruning, knowledge distillation, mixed precision training, and quantization aware training.
  • Each year, larger and larger models are able to find methods for extracting signal from the noise in machine learning. With the exponential increase in the parameter count of models, the computational requirements have also been blowing up exponentially (in both runtime and memory), which can be both costly when served out to customers or too slow or large to function in edge environments like a phone.
  • Researchers and practitioners have come up with many methods for optimizing neural networks to run faster or with less memory usage, enabling models to run efficiently on device (also called edge AI). This article covers some of the state-of-the-art methods to edge AI.

Quantization

Background: Precision

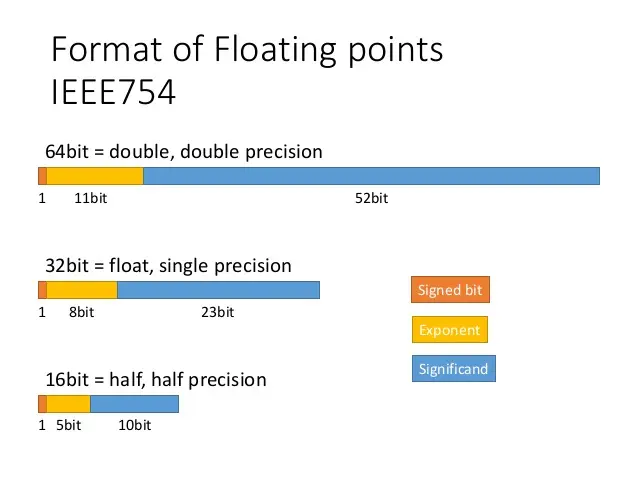
Definition

  • Quantization generally refers to taking a model with parameters (weights, in all cases and activations, in most cases) trained at high precision (32 or 64 bits) and reducing the number of bits that each weight takes (for example down to 16, 8, or even fewer). In practice, this usually leads to a speedup of 2-4x (highest for nets with convolutions, based on experience).

  • Model quantization reduces the precision of parameters, usually converting from 32-bit float to 8-bit integer representations. This achieves around 4x model compression. However, lower precision can cause the model to diverge from its original converged state. To address this, “quantization aware training” fine-tunes the model after quantization on additional data to regain performance. “Post training quantization” skips this fine-tuning step and instead applies heuristics to alter the quantized weights directly to try preserving model accuracy. In both cases, the goal of quantization is to dramatically shrink model size with minimal impact on model predictions. The fine-tuning counteracts the performance drops typical of reduced precision, making quantization a valuable model optimization.

  • Why does this work? It turns out that for deep networks to work, we don’t need highly precise values for the network’s weights. With proper hardware support, processing deep learning kernels (a fancy term for mathematical operations) using fewer bits can be faster and more memory efficient simply because there’s fewer bits to compute (torch.qint8 is 8 bits, and torch.float32 is 32 bits, so 4x smaller).

Downsides: Depending on the level of quantization attempted, you might find that an operation you want (for example, a particular convolutional op or even something as simple as transpose) might not be implemented. Of course, as with all methods, you might also find that accuracy drops off too much to be useful.

  • From the TensorFlow docs:

We generally recommend 16-bit floats for GPU acceleration and 8-bit integer for CPU execution.

Quantization with PyTorch

  • PyTorch has support for special quantized tensors, which in their case corresponds to storing data in 8 or 16 bits. It’s important to understand one specific detail about how this works. If your network has a special structure that means that at some point all of the outputs are between 0 and 1 (e.g., from a sigmoid), then you might be able to choose a better, more specific quantization. This means that quantization needs to collect some data about how your network runs on representative inputs. In particular, most quantization happens via a method like round(x * scalar), where scalar is a learned parameter (akin to BatchNorm).

Support for some of these operations are in libraries that are “external” to PyTorch (but loaded as required). Think of this like BLAS or MKL for quantized operations. FBGEMM is an implementation for servers, and QNNPACK is an implementation for mobile devices (now inside PyTorch proper).

  • Quantization occasionally has gotchas - accumulating in higher precision data types is often more stable than using lower precision values, especially if the input data has deep levels of an exponent. Picking the right precision for each operation can be nonobvious, so PyTorch has a torch.cuda.amp package to help you automatically cast different parts of your network to half precision (torch.float16) where it’s possible. If you want to do this manually, there’s some helpful tips on PyTorch: Automated Mixed Precision page.

One of the very first things you can try is to take your existing model that’s all torch.float32, and run it using torch.cuda.amp and see if it still runs with accuracy. Half precision support is still relatively sparse in consumer GPUs, but it works on the very common V100/P100/A100.

  • If you want more control or want to deploy to a non-CUDA environment, there are three levels of manual quantization (under the label “eager mode quantization”) that you can try, depending on why you’re trying to quantize and how much you’re willing to sweat:

    • Dynamic quantization: weights quantized with activations read/stored in floating point and quantized for compute
    • Static quantization: weights quantized, activations quantized, calibration required post training
    • Static quantization-aware training: weights quantized, activations quantized, quantization numerics modeled during training

  • Please see PyTorch: Introduction to Quantization on Pytorch blog post for a more comprehensive overview of the tradeoffs between these quantization types.

Note that layer/operator coverage (Linear/Conv/RNN/LSTM/GRU/Attention) varies between dynamic and static quantization and is captured in the table below. Note that for FX quantization, the corresponding functionals are also supported.

Dynamic/Runtime Quantization

  • The easiest method of quantization PyTorch supports is called dynamic quantization. This involves not just converting the weights to int8 - as happens in all quantization variants - but also converting the activations to int8 on the fly, just before doing the computation (hence “dynamic”). The computations will thus be performed using efficient int8 matrix multiplication and convolution implementations, resulting in faster compute. However, the activations are read and written to memory in floating point format.
  • In other words, we store the weights of the network in the specified quantization, and then at runtime, activations are dynamically converted to the quantized format, combined with the (quantized) weights, then written in memory at full precision. Then the next layer quantizes those, combines with the next quantized weights, and so on. Why does this happen? My understanding is that scalar can be dynamically determined from the data, which means this is a data-free method.
  • How do we do this in PyTorch? PyTorch offers have a simple API for dynamic quantization in PyTorch. torch.quantization.quantize_dynamic takes in a model, as well as a couple other arguments, and produces a quantized model! Check out this end-to-end tutorial illustrates this for a BERT model. As an example:
# quantize the LSTM and Linear parts of our network
# and use the torch.qint8 type to quantize
quantized_model = torch.quantization.quantize_dynamic(
    model, {nn.LSTM, nn.Linear}, dtype=torch.qint8
)
  • There are many more knobs you can turn to make this better for your model. See more details in this blog post.
  • See the documentation for the function here an end-to-end example in our tutorials here and here.

Post-Training Static Quantization

  • Runtime conversion to a full precision type and back is expensive. We can avoid that if we know what the distribution of activations will be, by say, recording real data flowing through the network.
  • One can further improve the performance (latency) by converting networks to use both integer arithmetic and int8 memory accesses. Static quantization performs the additional step of first feeding batches of data through the network and computing the resulting distributions of the different activations (specifically, this is done by inserting “observer” modules at different points that record these distributions). This information is used to determine how specifically the different activations should be quantized at inference time (a simple technique would be to simply divide the entire range of activations into 256 levels, but we support more sophisticated methods as well).
  • Importantly, this additional step allows us to pass quantized values between operations instead of converting these values to floats - and then back to ints - between every operation, resulting in a significant speed-up.

  • The following features are supported that allow users to optimize their static quantization:

    • Observers: you can customize observer modules which specify how statistics are collected prior to quantization to try out more advanced methods to quantize your data.
      • Observers are inserted using torch.quantization.prepare.
    • Operator fusion: When you have access to data flowing through your network, PyTorch can also inspect your model and implement extra optimizations such as quantized operator fusion. You can fuse multiple operations into a single operation, saving on memory access while also improving the operation’s numerical accuracy.
      • To fuse modules, use torch.quantization.fuse_modules.
    • Per-channel quantization: we can independently quantize weights for each output channel in a convolution/linear layer, which can lead to higher accuracy with almost the same speed.
      • Quantization itself is done using torch.quantization.convert.
  • Here’s an example of setting up the observers, running it with some data, and then exporting to a new statically quantized model:
# this is a default quantization config for mobile-based inference (ARM)
model.qconfig = torch.quantization.get_default_qconfig('qnnpack')
# or set quantization config for server (x86)
# model.qconfig = torch.quantization.get_default_config('fbgemm')

# this chain (conv + batchnorm + relu) is one of a few sequences 
# that are supported by the model fuser 
model_fused = torch.quantization.fuse_modules(model, [['conv', 'bn', 'relu']])

# insert observers
model_with_observers = torch.quantization.prepare(model_fused)

# calibrate the model and collect statistics
model_with_observers(example_batch)

# convert to quantized version
quantized_model = torch.quantization.convert(model_with_observers)

Static Quantization-aware Training (QAT)

  • Quantization-aware training (QAT) is the third method, and the one that typically results in highest accuracy of these three. With QAT, all weights and activations are “fake quantized” during both the forward and backward passes of training: that is, float values are rounded to mimic int8 values, but all computations are still done with floating point numbers. Thus, all the weight adjustments during training are made while “aware” of the fact that the model will ultimately be quantized; after quantizing, therefore, this method usually yields higher accuracy than the other two methods.
  • Put simply, if you tell the training method some fact about how the network is used, the network will adapt to this information. How does this work? During the forward and backward passes, the model’s activations are rounded to the picked quantization. This means the model gets gradients based on rounded values, which means it “adjusts” to its limited capacity.

Very importantly, however, the actual backprop (i.e., the gradient descent of the weights) happens in full precision.

  • torch.quantization.prepare_qat inserts fake quantization modules to model quantization. Mimicking the static quantization API, torch.quantization.convert actually quantizes the model once training is complete.

  • For example, in the end-to-end example, we load in a pre-trained model as qat_model, then we simply perform quantization-aware training using:

# specify quantization config for QAT
qat_model.qconfig=torch.quantization.get_default_qat_qconfig('fbgemm')

# prepare QAT
torch.quantization.prepare_qat(qat_model, inplace=True)

# convert to quantized version, removing dropout, to check for accuracy on each
epochquantized_model=torch.quantization.convert(qat_model.eval(), inplace=False)
  • Note: see the helpful tips under “Model Preparation for Quantization” here before using PyTorch quantization.

Device and Operator Support

  • Quantization support is restricted to a subset of available operators, depending on the method being used, for a list of supported operators, please see the documentation at here.

  • The set of available operators and the quantization numerics also depend on the backend being used to run quantized models. Currently quantized operators are supported only for CPU inference in the following backends: x86 and ARM. Both the quantization configuration (how tensors should be quantized and the quantized kernels (arithmetic with quantized tensors) are backend dependent. One can specify the backend by doing:

import torchbackend='fbgemm'

# 'fbgemm' for server, 'qnnpack' for mobile
my_model.qconfig = torch.quantization.get_default_qconfig(backend)

# prepare and convert model
# Set the backend on which the quantized kernels need to be run
torch.backends.quantized.engine=backend
  • However, quantization aware training occurs in full floating point and can run on either GPU or CPU. Quantization aware training is typically only used in CNN models when post training static or dynamic quantization doesn’t yield sufficient accuracy. This can occur with models that are highly optimized to achieve small size (such as Mobilenet).

Integration in torchvision

  • PyTorch has also enabled quantization for some of the most popular models in torchvision: Googlenet, Inception, Resnet, ResNeXt, Mobilenet and Shufflenet. We have upstreamed these changes to torchvision in three forms:

    1. Pre-trained quantized weights so that you can use them right away.
    2. Quantization ready model definitions so that you can do post-training quantization or quantization aware training.
    3. A script for doing quantization aware training — which is available for any of these model though, as you will learn below, we only found it necessary for achieving accuracy with Mobilenet.
    4. We also have a tutorial showing how you can do transfer learning with quantization using one of the torchvision models.

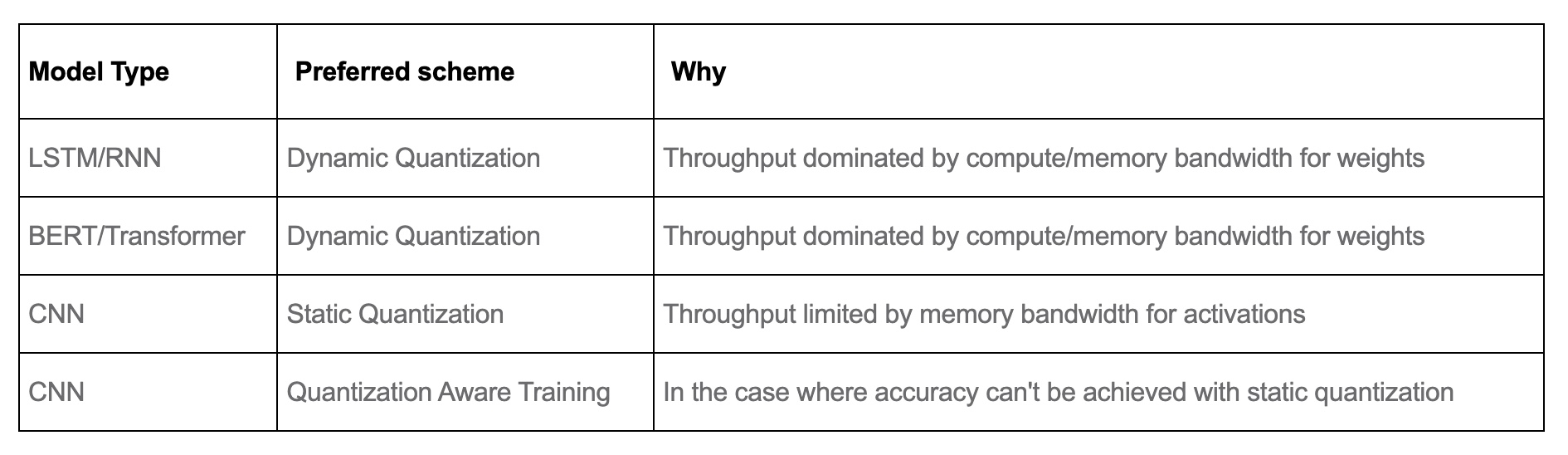
Choosing an approach

  • The choice of which scheme to use depends on multiple factors:

    • Model/Target requirements: Some models might be sensitive to quantization, requiring quantization aware training.
    • Operator/Backend support: Some backends require fully quantized operators.

  • Currently, operator coverage in PyTorch is limited and may restrict the choices listed in the table below. The table below from PyTorch: Introduction to Quantization on PyTorch provides a guideline.

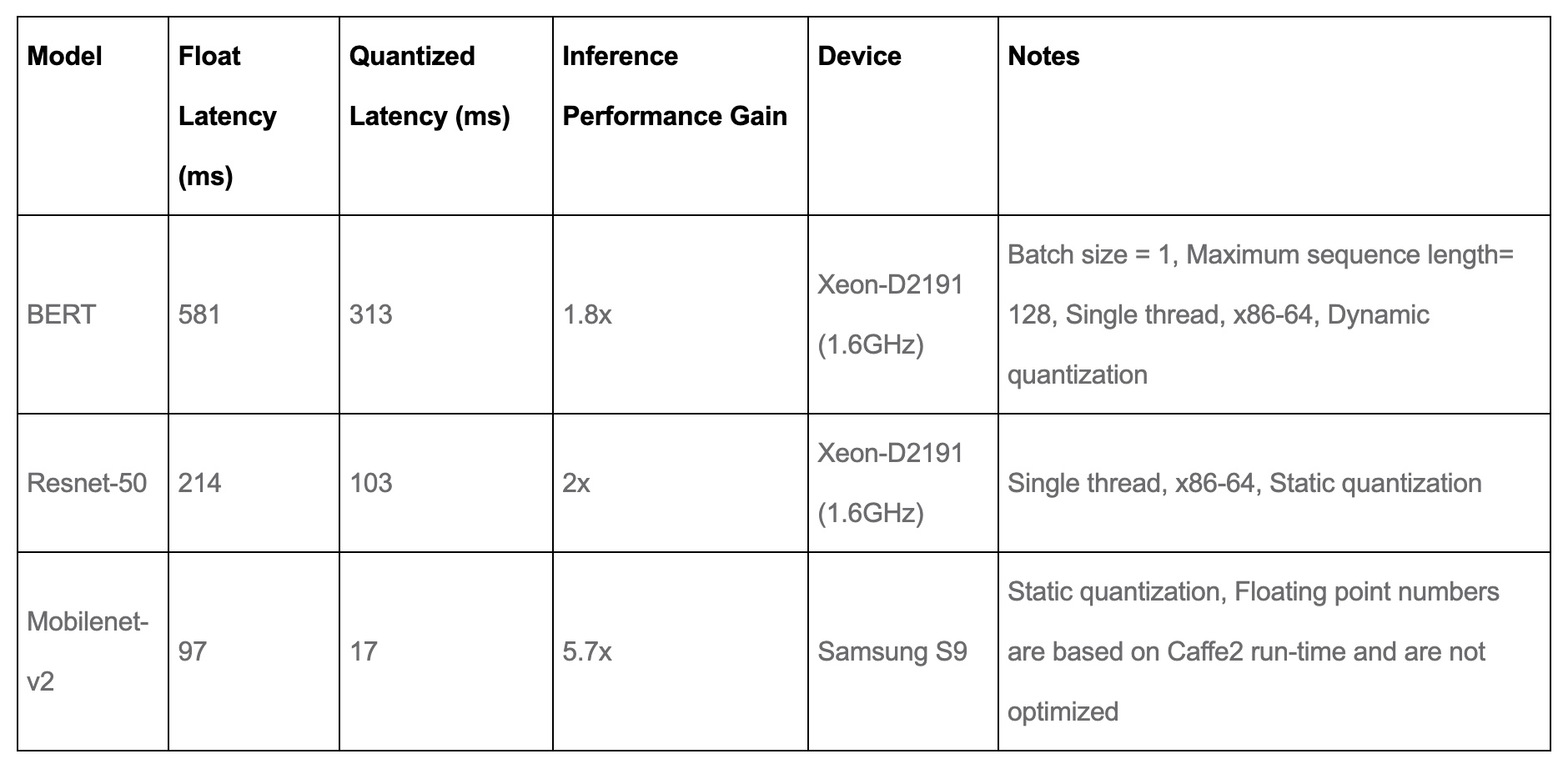
Performance Results

  • Quantization provides a 4x reduction in the model size and a speedup of 2x to 3x compared to floating point implementations depending on the hardware platform and the model being benchmarked. The table below from PyTorch: Introduction to Quantization on PyTorch offers some sample results:

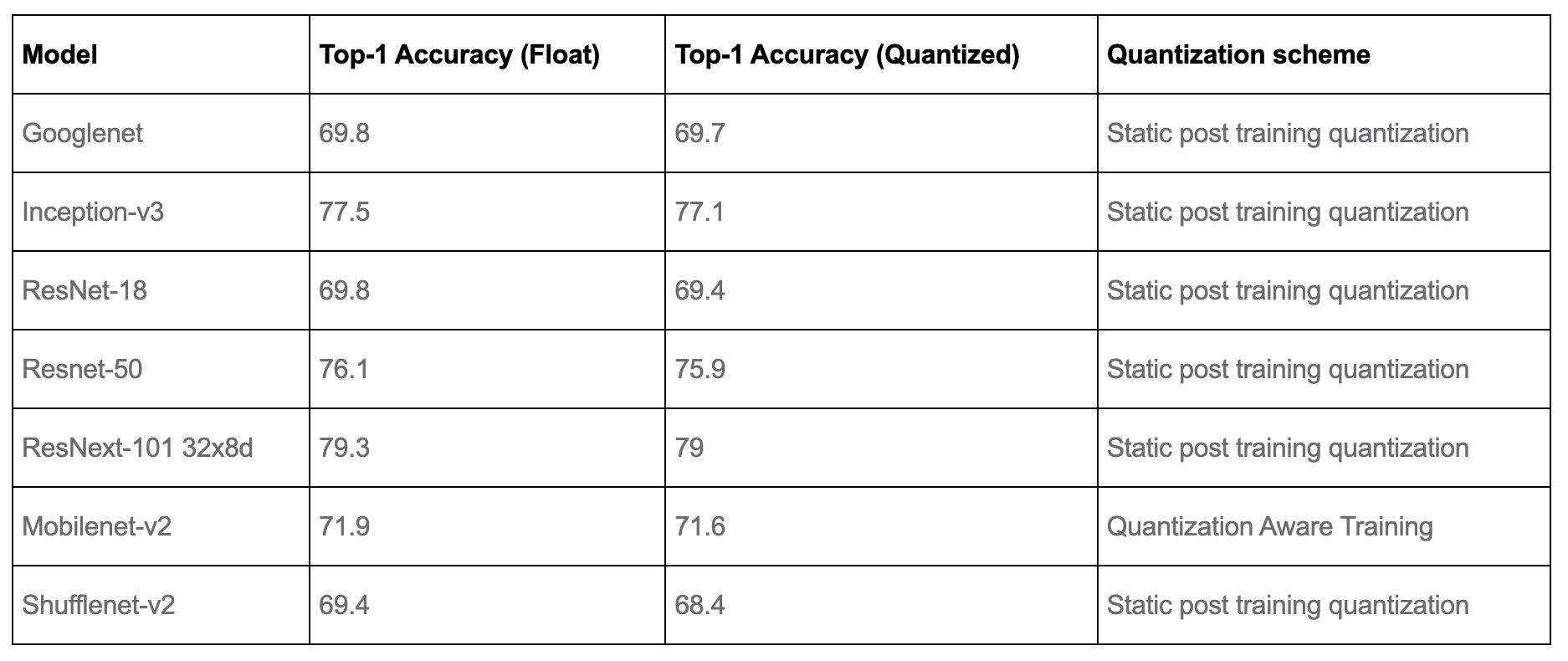
Accuracy results

  • The tables below from PyTorch: Introduction to Quantization on PyTorch compares the accuracy of static quantized models with the floating point models on Imagenet. For dynamic quantization, we compared the F1 score of BERT on the GLUE benchmark for MRPC.

Computer Vision Model accuracy

Speech and NLP Model accuracy

Conclusion

Quantization in other frameworks: TensorFlow and CoreML

  • PyTorch-based quantization might not necessarily work in other production environments. In particular, when converting to Apple’s CoreML format, you need to just use their quantization (which might be limited to just 16-bit quantization). When using edge devices, be careful to check that quantization is possible (in Apple’s case the hardware is already computing everything in fp16 on GPU, so you only save possibly the memory of the network’s weights).

  • TensorFlow has a similar set of steps as above, though the examples are focused on TFLite. Essentially, static and dynamic quantization are explained in the Post-training quantization page, and there’s a QAT page. The tradeoffs appear to be very similar, though there’s always some feature mismatch between PyTorch and TF.

How far can we go?

  • Apparently down to 1 bit! There have been several attempts over the years to create binary neural networks if you want the most extreme version of the accuracy vs speed tradeoff. For the most part, these are still research projects rather than usable ideas, though XNOR-Net++ seems to have been implemented in PyTorch.

Use-case

  • Quantization’s goal is to increase inference speed. (In contrast, as we’ll see in the section on Mixed Precision Training, Automatic Mixed Precision (AMP)’s main goal is to reduce training time.)

Further Reading

Knowledge distillation

  • Knowledge distillation is a method for creating smaller and more efficient models from large models, in which the large model (teacher) trains the smaller model (student). The reference work in this area is Hinton et al., 2015.

  • “Knowledge distillation is about transferring knowledge from one model to another. Typically from a large model to a smaller one. When the student model learns to produce similar output responses, that is response-based distillation. When the student model learns to reproduce similar intermediate layers, it is called feature-based distillation. When the student model learns to reproduce the interaction between layers, it is called relation-based distillation.” source: AiEdge.io

  • The image below (source: AiEdge.io), does a great job at illustrating this concept.

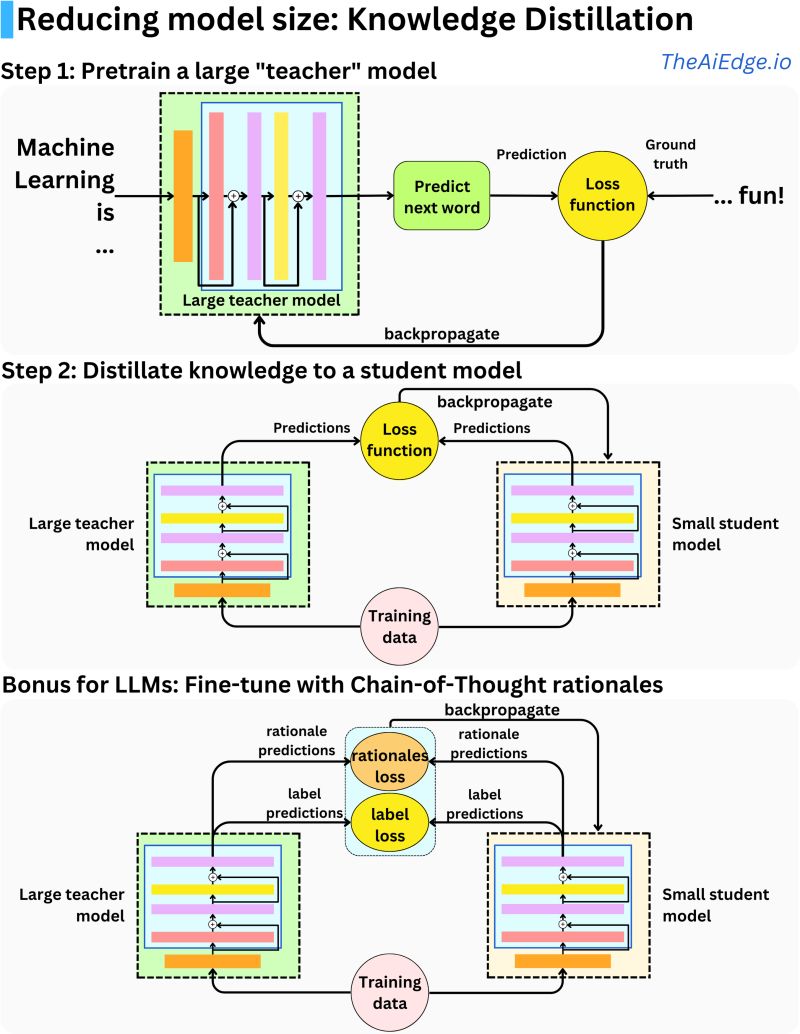
  • Knowledge distillation is a mechanism that lets us deploy a relatively large deep learning model in production. Specifically, knowledge distillation trains a smaller model, the student, to mimic the generalization power of a larger model, the teacher.

The key idea is that, instead of training the student with the same labeled data as the teacher, we use the output probability distribution of the teacher as a soft target to train the small model.

  • Put simply, knowledge distillation is a technique where a smaller model (the student) is trained to imitate the behavior of a larger, typically pre-trained model (the teacher). The goal is to have the student model, which is more compact and computationally efficient, retain as much of the teacher model’s performance as possible.
  • The main idea behind knowledge distillation is to transfer the “knowledge” encoded in the teacher’s soft output probabilities (logits) to the student, rather than just the hard label assignments. Soft probabilities carry more information about the data distribution and the teacher’s internal representations.
  • In a standard training process, the teacher learns to discriminate between many classes and maximizes the probability of the correct label. However, a side-effect is that the model assigns smaller probabilities to other classes, which can give us a lot of knowledge about how the model generalizes. For example, an image of a cat can have a low probability of being mistaken for a tiger, but that mistake is still many times more probable than mistaking it for a chair. We can take advantage of this knowledge to improve the student.
  • The student is a network with fewer parameters than the teacher. However, it is recommended to use the same structure, for example, if we want BERT as a teacher, we can use DistillBERT, which has 40% fewer parameters.
  • The student training loss is a combination of the original training loss of the teacher and a distillation loss. The distillation loss simply softens the probability distribution of the correct classes by scaling it with a temperature parameter.
  • The effect is this temperature is effectively reducing the higher probabilities and increasing the smaller ones, to make a softer distribution that has more knowledge.
  • Knowledge distillation can cut the latency of a machine learning model by half at the cost of reducing the model’s accuracy minimally.

  • In practice, suppose we have a classification task. Suppose our smaller student model is \(f_{\theta}\), where $\theta$ is the set of parameters. We take either a large model or an ensemble of models (possibly even the same model trained with different initializations), and call it $F$ (we won’t worry about its parameters). Then we train the student network with the following loss:

    \[\mathcal{L}=\sum_{i=1}^{n} \mathrm{KL}\left(F\left(x_{i}\right), f_{\theta}\left(x_{i}\right)\right)\]
    • where \(F\left(x_{i}\right)\) is the probability distribution over the labels created by passing example \(x_{i}\) through the network.
  • If you want, you can add in the regular cross entropy loss using the proper labels (by passing in the one-hot ground truth distribution to the student as well):
\[\mathcal{L}=\sum_{i=1}^{n}\left(\mathrm{KL}\left(F\left(x_{i}\right), f_{\theta}\left(x_{i}\right)\right)-\beta \cdot \sum_{k=1}^{K} y_{i}[k] \log f_{\theta}\left(x_{i}\right)[k]\right)\]
  • Note that this second term is just the KL divergence (can also be cross entropy loss) from the “true” distribution (i.e., the one-hot distribution from the labels) to the student model, since is one-hot.
  • In summary, the loss function in knowledge distillation is a combination of two terms:
    1. Distillation Loss (Soft Loss): This is the main component of the distillation process. It computes the difference between the teacher’s soft output probabilities and the student’s soft output probabilities. The soft probabilities are typically obtained using a softmax function with a temperature parameter \(T\): \(\text{Softmax}(z_i) = \frac{\exp(z_i/T)}{\sum_j \exp(z_j/T)}\) - where \(z_i\) are the logits (pre-softmax outputs) of the model. The temperature \(T\) is used to control the softness of the probabilities. A higher value of \(T\) produces softer probabilities, which are more informative for the distillation process.
      • The distillation loss can be computed using the Kullback-Leibler divergence between the soft probabilities of the teacher and the student: \(L_{\text{distill}} = \text{KL} \left( \text{Softmax}(z_{\text{teacher}}/T) || \text{Softmax}(z_{\text{student}}/T) \right)\)
    2. Ground Truth Loss (Hard Loss): This is a traditional supervised learning loss computed between the student’s outputs and the true labels of the data. Common choices for this loss include cross-entropy for classification tasks.
      • The overall loss function for knowledge distillation is a weighted combination of the distillation loss and the ground truth loss: \(L = \alpha L_{\text{hard}} + (1 - \alpha) L_{\text{distill}}\)
        • where \(\alpha\) is a hyperparameter to balance the two losses.
      • This combined loss function helps the student model to generalize better by leveraging both the ground truth labels and the rich knowledge embedded in the teacher’s soft outputs.
  • Why does this work? There’s no consensus in the field. The most compelling explanation is that distillation is a form of rough data augmentation. This paper is recommended to understand why: Towards Understanding Ensemble, Knowledge Distillation and Self-Distillation in Deep Learning, which is focused on the idea of multiple views. Here’s some thought experiments that might help explain what’s happening under-the-hood.

Distillation thought experiment

  • Let’s say that we have a large teacher model that is trained to classify images (e.g., CIFAR-100). This model implicitly has a bunch of “feature-detectors” built-in, e.g., a set of convolutional filters that fire when pointy ears are seen, which increase the probability of a label like “cat”. Let’s say that there’s a training image of a Batman mask, labeled “mask”. The teacher model’s pointy ears filters might still fire, telling us that the model thinks that this looks 10% like a cat.

  • When the student model is trained to match the probability distribution of the teacher, because the distribution is 0.1 cat, it will still get a small signal that this image is catlike, which might help the student model recognize cats better than it could otherwise. If the student model was trained on just the true labels, it would have no idea that this Batman mask looks a bit like a cat. This logic also supports why the student can out-perform the teacher in some cases.

Ensembling thought experiment

  • A similar, but slightly different idea explains why ensembles of models (even the same architecture) might work well. Let’s say there’s 3 pictures of a cat in a dataset we’re using for image classification. Let’s say that image 1 has a cat with feature A (e.g., pointed ears), image 2 has feature B (e.g., whiskers), and image 3 has both A and B.

  • Then, let’s say the neural network learns feature A (e.g., by seeing image 1). When it sees image 3, that set of convolution filters will fire, and so the image will be correctly classified. So, there’ll be no gradient that tunes the net to recognize feature B, even though a good net would learn that.

  • Once a neural network has become good enough, its signal from some data points decreases.

Distillation in practice

  • Knowledge distillation is a very deep and wide research area, touching adversarial attacks, knowledge transfer, and privacy.

  • In practice, the method described above is called response-based distillation. There are also other forms of distillation, including feature-based and relation-based knowledge distillation, which are entire subfields based on what parts (or computations from) the student and teacher model we should tie together.

  • Furthermore, there’s a division between offline distillation (i.e., train the student after the teacher), online distillation (train the student and teacher together), and self-distillation (where the teacher model has the same architecture as the student). Together this makes it difficult to track distillation in practice; a set of adhoc model-specific techniques might be the best general recommendation.

  • In fact, Cho & Hariharan, 2019 found that when the student model’s capacity is too low, using knowledge distillation will actually adversely affect training. They found that knowledge distillation papers rarely use ImageNet and so often don’t work well on difficult problems. Perplexingly, that paper and Mirzadeh et al., 2019 found that better teacher models don’t always mean better distillation, and the farther the student and teacher model’s capacities are, the less effective distillation was. You can find a recent investigation in Tang et al., 2021.

  • All in all, distillation is relatively difficult compared to quantization and pruning. You might be able to get some free performance points by training a student with a slightly smaller capacity and then using vanilla response-based offline distillation.

Weak supervision: Distillation as semi-supervised learning

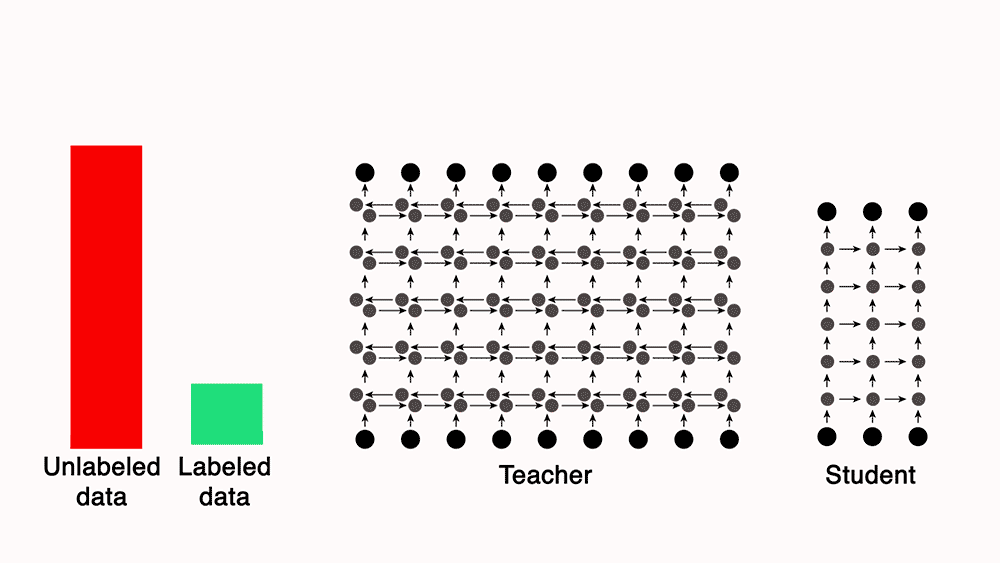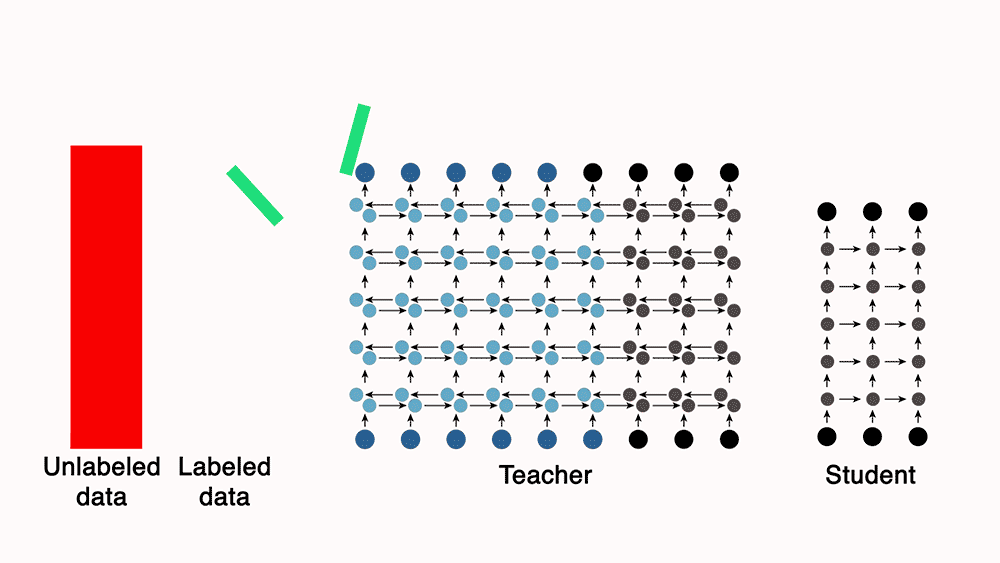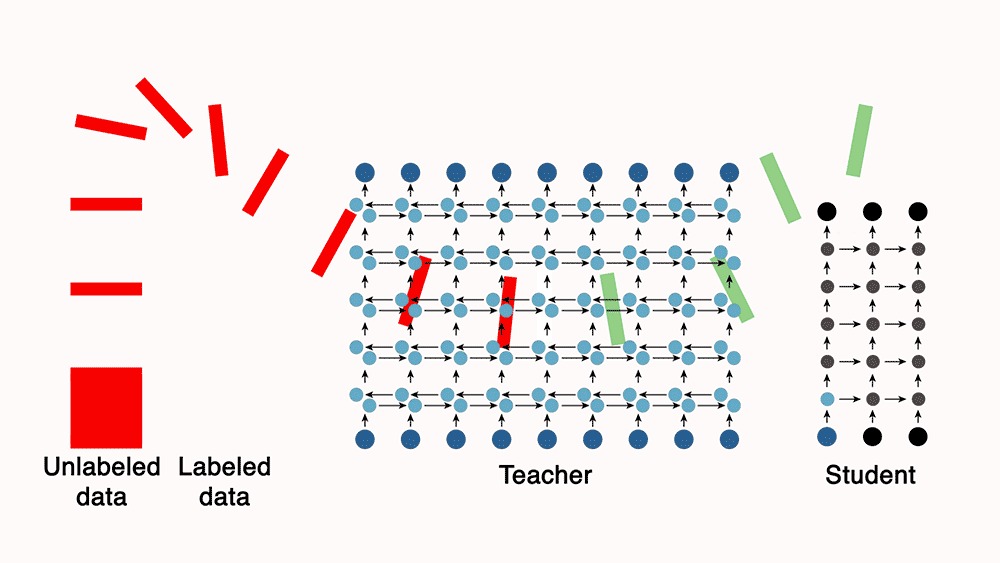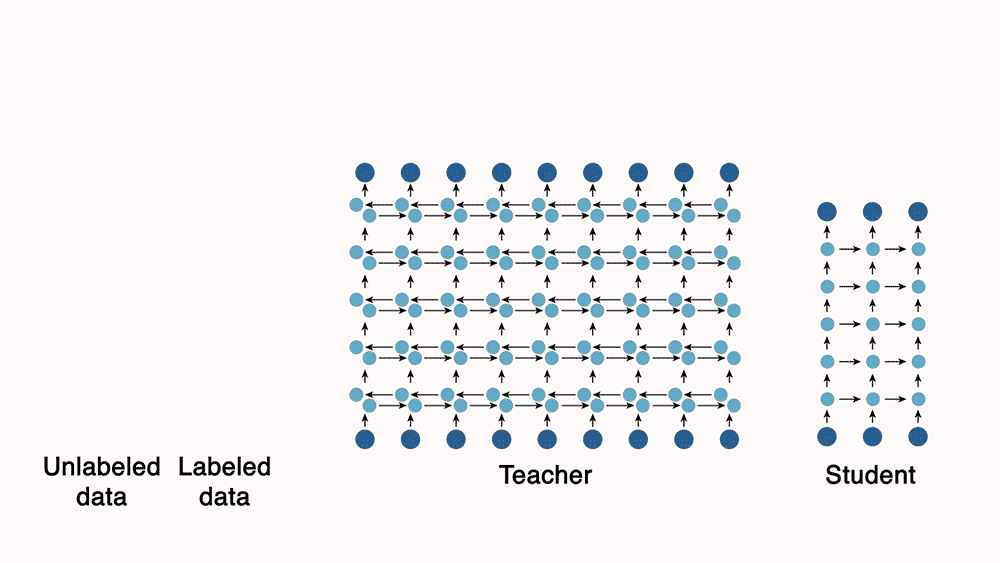
  • You can train a teacher model, which is a much more powerful model than the student, with a small set of labeled data. Next, use the teacher to automatically label unannotated data, which can be used to train a leaner, more efficient “student” network.
  • For e.g., Lessons from building acoustic models with a million hours of speech by Parthasarathi and Strom (2019), used a small set of annotated data (green) to train a powerful but impractically slow “teacher” network to convert frequency-level descriptions of audio data into sequences of phones. The teacher, in turn, labeled a much larger set of unannotated data (red). They then used both datasets to train a leaner, more efficient “student” model.

Reverse distillation

  • Based on Investigating the Impact of Model Width and Density on Generalization in Presence of Label Noise, we see that large models are more susceptible to overfitting on noise in the dataset due to over-parameterization and this can hurt the performance as we scale. This is especially true for datasets with high label noise (e.g., CTR data collected through user-interactions in a weak supervision manner).
  • In order to overcome this and help the larger models learn better on inherently noisy datasets, a potential method could be training large models by leveraging knowledge from smaller models using a process called reverse distillation. Put simply, (we transfer knowledge from smaller models to larger models as part of reverse distillation.
  • In this method, we first train a smaller model and then use this smaller model as a teacher to guide the training of much larger models.
  • The hypothesis is that the soft labels help the large model generalize much better on noisy datasets and also improve the stability of training larger models.

Pruning

  • Pruning is removing some weights (i.e., connections) or entire neurons from a neural network after or during training. In practice, we can often remove 90% of the parameters in large deep neural networks without significantly affecting model performance.

  • Model pruning ultimately looks to remove unimportant weights from the network by learning which weights are actually important. Common techniques for neural network pruning involve analyzing the effect each weight has on the overall loss function. The gradient and second derivative of the loss with respect to each weight gives a sense of impact. Regularization methods like L1 and L2 that drive small magnitude weights to zero are also useful. More advanced “structured pruning” removes entire neurons, layers, or filters based on their cumulative impact, giving better optimization for inference speed. The goal of all these pruning approaches is to reduce redundant or non-essential parts of the model without significantly hurting loss function performance. This results in a slimmer, more efficient model.

  • Why does this work? Let’s imagine that your model is a fully connected neural network with just one hidden layer, such that the input is size 1024, the hidden size is 100, and the output is 20 dimensions. Then the number of parameters (without bias) is 104400. If there’s a neuron in the hidden layer that never fires (or is ignored downstream) then removing it from the network saves 1044 parameters. Why not just train the smaller network right away? The most compelling explanation is something called the lottery ticket hypothesis:

Any large network that trains successfully contains a subnetwork that is initialized such that - when trained in isolation - it can match the accuracy of the original network in at most the same number of training iterations.

Structured vs. Unstructured pruning

  • Removing neurons or choosing a subnetwork is what people consider structured pruning. However, a lot of methods (including TensorFlow’s tensorflow_model_optimization toolkit at this time and PyTorch’s torch.nn.utils.prune) are focused on sparsifying model weights so that they are more compressible (usually called unstructured pruning). This means the matrices are the same size, but some values are set to 0. This can save disk space using compression algorithms (such as run-length encoding or byte-pair encoding). When sparse model support fully lands in the various frameworks (i.e., you can multiply a sparse vector and a sparse matrix faster than the dense ones) you might be able to speed up inference as well.

  • For that reason, unstructured pruning (currently) doesn’t seem that useful, but essentially you can prune during or after training, and you pick a certain target sparsity (e.g., 80% of the weights of your network will be zeroed out). However, there’s a lot of confusion in this area which makes it hard to recommend anything. TensorFlow has a a few guides on pruning both during and after training and PyTorch has a tutorial on pruning using some set of heuristics after training.

  • In the space of structured pruning, there’s still active research and no clear API. We can pick a metric to compute a relevance score for each neuron, and then remove the ones that have the least information content. Metrics that might be useful here are the Shapley value, a Taylor approximation of the loss functions sensitivity to a neuron’s activation, or even a random neuron. Before you begin, check out PyTorch: Pruning Tutorial. The TorchPruner library implements some of these automatically for nn.Linear and convolutions (nn.Conv1D, nn.Conv2D, etc) modules. Another library Torch-Pruning has support for a few more operations. One of the most well-known older works in this area prunes filters from a convnet using the L1 norm of the filter’s weights. However, this is still an active area of research.

Fine tuning

  • In both cases, it’s standard to retrain the network after applying the pruning. Currently, the best method is basically to reset the learning rate (learning rate rewinding) and start retraining the network. If you’d like, you can use weight rewinding, which is resetting the weights for the unpruned parts of the network to their value earlier in training (e.g., 1/3 trained weights). My intuition on this is that it’s essentially training the lottery ticket subnetwork now that we’ve identified it.

Overall, a practitioner who is really interested in trying this should start with TorchPruner or Torch-Pruning and then try fine tuning the resulting network with learning rate rewinding. However, for most architectures (including ResNets because of skip connections) it’ll be pretty non-obvious how to trim the rest of the network around this.

DeepSpeed and ZeRO-Offload

  • Essentially, DeepSpeed is a library that helps train large to extremely large models (e.g., 1bn+ parameters) faster and using less GPU memory. This works by exploiting smart parallelism and better caching. It comes in the form of an extension to PyTorch.

Conclusion

  • Deep learning researchers have spent a lot of time distilling large models using model-specific methods, and if you need to gain some performance, you might be able to find a pre-trained distilled version of the large model you’re currently using. For example, in NLP, HuggingFace makes it easy to access both DistilBert and TinyBert. In computer vision, Facebook Research’s d2go has a bunch of pretrained mobile-ready models, and they’ve specialized some distillation methods in DeiT.

  • Well-Read Students Learn Better: On the Importance of Pre-training Compact Models makes a recommendation (with high quality ablation experiments) that for training BERT architectures, the best approach is:

    1. Pre-train a compact model architecture on the masked language model (MLM) objective developed by the original BERT papers (Devlin et al., 2018).
    2. Take a large task-specific teacher model (e.g., if the task is NLI, the output is a distribution over the 3 classes (entailment, contradiction, neutral)), and perform basic response-based offline distillation on the pre-trained compact model from step 1.
    3. Finally, if required, fine-tune the compact model from step 2 on the task-specific data (e.g., if the task is NER, train over the CoNLL 2003 dataset).

  • One of the best advantages of this method (which they call Pre-trained Distillation (PD)) is that it’s architecture-agnostic. If you are going to use a compact NLP model in practice, it’s worth skimming the paper, especially section 6.

Mixed Precision Training

Overview

  • Mixed precision is a technique for substantially reducing neural net training time by performing as many operations as possible in half-precision floating point, float16, instead of the (PyTorch default) single-precision floating point, float32 – it thus involves the use of both 16-bit and 32-bit floating-point types during training to make it run faster and use less memory. By keeping certain parts of the model in the 32-bit types for numeric stability, the model will have a lower step time and train equally as well in terms of the evaluation metrics such as accuracy.
    • The term “numeric stability” refers to how a model’s quality is affected by the use of a lower-precision dtype instead of a higher precision dtype. An operation is “numerically unstable” in float16 or bfloat16 if running it in one of those dtypes causes the model to have worse evaluation accuracy or other metrics compared to running the operation in float32.
  • Today, most models use the float32 dtype, which takes 32 bits of memory. However, there are two lower-precision dtypes, float16 and bfloat16, each which take 16 bits of memory instead. Modern accelerators can run operations faster in the 16-bit dtypes, as they have specialized hardware to run 16-bit computations and 16-bit dtypes can be read from memory faster.
  • Put simply, the idea behind Automatic Mixed Precision (AMP) is that not all layers and operations require the precision of float32, hence it’s better to use lower precision. AMP takes care of what precision to use for what operation. It eventually helps speed up the training.
  • Mixed precision tries to match each op to its appropriate datatype, which as a by-product, can reduce your network’s runtime and memory footprint.

Under-the-hood

  • NVIDIA GPUs can run operations in float16 faster than in float32, and TPUs can run operations in bfloat16 faster than float32. Therefore, these lower-precision dtypes should be used whenever possible on those devices. However, variables and a few computations should still be in float32 for numeric reasons so that the model trains to the same quality (cf. numerical stability in the section on Mixed Precision Overview).
  • Recent generations of NVIDIA GPUs come loaded with special-purpose tensor cores specially designed for fast fp16 matrix operations. Thus, max performance gains are observed on Tensor Core-enabled GPU architectures as we’ll see below in the section on How Tensor Cores Work.
  • However, up until now these tensor cores have remained difficult to use, as it has required writing reduced precision operations into your model by hand. This is where the automatic in automatic mixed-precision training comes in. The [torch.cuda.amp]() API allows you to implement mixed precision training into your training scripts in just five lines of code!

How mixed precision works

  • Before we understand how mixed precision training works, let’s review a little bit about floating point numbers.
  • In computer engineering, decimal numbers like 1.0151 or 566132.8 are traditionally represented as floating point numbers. Since we can have infinitely precise numbers (think \(\pi\)), but limited space in which to store them, we have to make a compromise between precision (the number of decimals we can include in a number before we have to start rounding it) and size (how many bits we use to store the number).
  • Building upon what we discussed in the Background: Precision, the technical standard for floating point numbers, IEEE 754 (for a deep dive please refer to the PyCon 2019 talk “Floats are Friends: making the most of IEEE754.00000000000000002”), sets the following standards:
    • fp64, aka double-precision or “double”, max rounding error of ~\(2^-{52}\).
    • fp32, aka single-precision or “single”, max rounding error of ~\(2^-{23}\).
    • fp16, aka half-precision or “half”, max rounding error of ~\(2^-{10}\).
  • Python uses fp64 for the float type. PyTorch, which is much more memory-sensitive, uses fp32 as its default dtype instead.

The basic idea behind mixed precision training is simple: halve the precision (fp32 \(\rightarrow\) fp16), halve the training time.

  • The hard part is doing so safely.
  • Notice that the smaller the floating point, the larger the rounding errors it incurs. Any operation performed on a “small enough” floating point number will round the value to zero! This is known as underflowing, and it’s a problem because many to most gradient update values created during backpropogation are extremely small but nevertheless non-zero. Rounding error accumulation during backpropogation can turn these numbers into zeroes or nans; this creates inaccurate gradient updates and prevents your network from converging.
  • The 2018 ICLR paper Mixed Precision Training found that naively using fp16 everywhere “swallows” gradient updates smaller than \(2^{-24}\) in value — around 5% of all gradient updates made by their example network:

  • Mixed precision training is a set of techniques which allows you to use fp16 without causing your model training to diverge. It’s a combination of three different techniques.
    1. Maintain two copies of the weights matrix, a “master copy” in fp32, and a half-precision copy of it in fp16. Gradient updates are calculated using the fp16 matrix but applied to the fp32 matrix. This makes applying the gradient update much safer.
    2. Different vector operations accumulate errors at different rates, so treat them differently. Some operations are always safe in fp16, but others are only reliable in fp32. Instead of running the entire neural network in fp16, run some parts in halves and others in singles. This mixture of dtypes is why this technique is called “mixed precision”.
    3. Use loss/gradient scaling. Loss scaling means multiplying the output of the loss function by some scalar number (the paper suggests starting with 8) before performing back-propagation. Multiplicative increases in the loss values create multiplicative increases in gradient update values, “lifting” many gradient update values above the \(2^{-24}\) threshold for fp16 safety. Just make sure to undo the loss scaling before applying the gradient update, and don’t pick a loss scaling so large that it produces inf weight updates (overflowing), causing the network to diverge in the other direction.
  • Combining these three techniques in tandem allowed the authors to train a variety of networks to convergence in significantly expedited time. For benchmarks, please refer the paper.

How tensor cores work

  • While mixed precision training saves memory everywhere (an fp16 matrix is half the size of a fp32 one), it doesn’t provide a model training speedup without special GPU support. There needs to be something on the chip that accelerates half-precision operations. In recent generations of NVIDIA GPUs, there is: tensor cores.
  • Tensor cores are a new type of processing unit that’s optimized for a single very specific operation: multiplying two \(4 \times 4\) fp16 matrices together and adding the result to a third \(4 \times 4\) fp16 or fp32 matrix (a “fused multiply add”).

  • Larger fp16 matrix multiplication operations can be implemented using this operation as their basic building block. And since most of backpropagation boils down to matrix multiplication, tensor cores are applicable to almost any computationally intensive layer in the network.

The catch: the input matrices must be in fp16. If you’re training on a GPU with tensor cores and not using mixed precision training, you’re not getting 100% out of your GPU! A standard PyTorch model defined in fp32 will never land any fp16 math onto the chip, so all of those fp16 cores will remain idle.

  • Tensor cores were introduced in late 2017 in the last-gen Volta architecture, saw improvement in current-gen Turing, and will see further refinements in the still-forthcoming Ampere. The two GPUs generally available on the cloud that support are the V100 (5120 CUDA cores, 600 tensor cores) and the T4 (2560 CUDA cores, 320 tensor cores).
  • One other piece of the puzzle worth keeping in mind is firmware. Although all versions of CUDA 7.0 or higher supports tensor core operations, early implementations are reputedly very buggy, so it’s important to be on CUDA 10.0 or higher.

How PyTorch automatic mixed precision works

  • With that important background out of the way, we’re finally ready to dig into the new PyTorch amp API.

  • Mixed precision training has technically been possible forever: run sections of your network in fp16 manually and implement loss scaling yourself. The exciting thing in automatic mixed-precision training is the “automatic” part. There’s just a couple of new API primitives to learn: torch.cuda.amp.GradScalar and torch.cuda.amp.autocast. Enabling mixed precision training is as simple as slotting these into the right places in your training script!

  • To demonstrate, here’s an excerpt of the training loop for a network using mixed-precision training. # NEW marks spots where new code got added.

self.train()
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.float32)

optimizer = torch.optim.Adam(self.parameters(), lr=self.max_lr)
scheduler = torch.optim.lr_scheduler.OneCycleLR(
    optimizer, self.max_lr,
    cycle_momentum=False,
    epochs=self.n_epochs,
    steps_per_epoch=int(np.ceil(len(X) / self.batch_size)),
)
batches = torch.utils.data.DataLoader(
    torch.utils.data.TensorDataset(X, y),
    batch_size=self.batch_size, shuffle=True
)

# NEW
scaler = torch.cuda.amp.GradScaler()

for epoch in range(self.n_epochs):
    for i, (X_batch, y_batch) in enumerate(batches):
        X_batch = X_batch.cuda()
        y_batch = y_batch.cuda()
        optimizer.zero_grad()

        # NEW
        with torch.cuda.amp.autocast():
            y_pred = model(X_batch).squeeze()
            loss = self.loss_fn(y_pred, y_batch)

        # NEW
        scaler.scale(loss).backward()
        lv = loss.detach().cpu().numpy()
        if i % 100 == 0:
            print(f"Epoch {epoch + 1}/{self.n_epochs}; Batch {i}; Loss {lv}")

        # NEW
        scaler.step(optimizer)
        scaler.update()
        
        scheduler.step()

Loss/Gradient Scaling

  • If the forward pass for a particular op has float16 inputs, the backward pass for that op will produce float16 gradients. Gradient values with small magnitudes may not be representable in float16. These values will flush to zero (“underflow”), so the update for the corresponding parameters will be lost.
  • To prevent underflow, “gradient scaling” multiplies the network’s loss(es) by a scale factor and invokes a backward pass on the scaled loss(es). Gradients flowing backward through the network are then scaled by the same factor. In other words, gradient values have a larger magnitude, so they don’t flush to zero.

  • The new PyTorch GradScaler object is PyTorch’s implementation of loss scaling. Recall from the section “How mixed precision works” that some form of loss scaling is necessary to keep gradients from rounding down to 0 during training. The optimal loss multiplier is one sufficiently high to retain very small gradients, but not so high that it causes very large gradients to round up to inf, creating the opposite problem.

  • However, there is no one loss multiplier that will work for every network. The optimal multiplier is also very likely to change over time, as gradients are typically much larger at the start of training than at the end. How do you find the optimal loss multiplier without giving the user another hyperparameter that they have to tune?

  • PyTorch uses exponential backoff to solve this problem. GradScalar starts with a small loss multiplier, which every so often it doubles. This gradual doubling behavior continues until GradScalar encounters a gradient update containing inf values. GradScalar discards this batch (e.g. the gradient update is skipped), halves the loss multiplier, and resets its doubling cooldown.

  • Stepping the loss multiplier up and down in this way allows PyTorch to approximate the appropriate loss multiplier over time. Readers familiar with TCP congestion control should find the core ideas here very familiar! The exact numbers used by the algorithm are configurable, and you can read the defaults right out of the docstring:
torch.cuda.amp.GradScaler(
    init_scale=65536.0, growth_factor=2.0, backoff_factor=0.5,
    growth_interval=2000, enabled=True
)

  • GradScalar needs to exert control over the gradient update calculations (to check for overflow) and over the optimizer (to turn discarded batches into a no-op) to implement its behavior. This is why loss.backwards() is replaced with scaler.scale(loss).backwards() and optimizer.step() is replaced with scaler.step(optimizer).

  • It’s notable that GradScalar will detect and stop overflows (because inf is always bad), but it has no way to detect and stop underflows (because 0 is often a legitimate value). If you pick an init_scale that’s too low and a growth_interval that’s too high, your network may underflow and diverge before GradScalar can intervene. For this reason it’s probably a good idea to pick a very large starting value, and with default init_scale=65536 (\(2^{16}\)) that does seem to be the approach that PyTorch is following.

  • Finally, note that GradScalar is a stateful object. Checkpointing a model using this feature will require writing it to and reading it from disk in alongside your model weights. This is easy to do using the state_dict and load_state_dict object methods (covered here in the PyTorch docs).
  • As an implementation detail, note that in PyTorch, each parameter’s gradient (.grad attribute) should be unscaled before the optimizer updates the parameters, so the scale factor does not interfere with the learning rate.

autocast context manager

  • The other half of the automatic mixed-precision training puzzle is the torch.cuda.amp.autocast context manager. Autocast implements fp32 -> fp16 behavior. Recall from “How mixed precision works” that, because different operations accumulate errors at different rates, not all operations are safe to run in fp16. The following screenshots taken from the amp module documentation covers how autocast treats the various operations available in PyTorch:

  • This list predominantly consists of two things, matrix multiplication and convolutions. The simple linear function is also present.

  • These operations are safe in fp16, but have up-casting rules to ensure that they don’t break when given a mixture of fp16 and fp32 input. Note that this list includes two other fundamental linear algebraic operations: matrix/vector dot products and vector cross products.

  • Logarithms, exponents, trigonometric functions, normal functions, discrete functions, and (large) sums are unsafe in fp16 and must be performed in fp32.

  • Looking through the list, it seems to me that most layers would benefit from autocasting, thanks to their internal reliance on fundamental linear algebra operations, but most activation functions would not. Convolutional layers stand out as potentially the biggest winner.

  • Enabling autocasting is pretty simple. All you need to do is wrap the forward pass of your model using the autocast context manager:

with torch.cuda.amp.autocast():
    y_pred = model(X_batch).squeeze()
    loss = self.loss_fn(y_pred, y_batch)
  • Wrapping the forward pass in this way automatically enables autocasting on the backwards pass (e.g. loss.backwards()) as well, so you don’t need to call autocast twice.
  • So long as you follow best practices for using PyTorch (avoiding in-place operations, for example), autocasting basically “just works”.

Multiple GPUs

Mixed Precision with TensorFlow

Performance benchmarks

  • Let’s look at some real-world performance benchmarks over three very different neural networks with and without automatic mixed precision. The training setup involved V100s (last-gen tensor cores) and T4s (current-gen tensor cores), using the Spell API on AWS EC2 instances, p3.2xlarge and g4dn.xlarge respectively, and a recent PyTorch build with CUDA 10.0.
  • All of the models converged equally, e.g. none of the models saw any difference in training loss between the mixed precision and vanilla network. The networks trained were:
  • The results:

  • Observations from the results:
  • Because the feedforward network is very small, it gets no benefit from mixed precision training.
  • UNet, a medium-sized convolutional model with 7,703,497 total parameters, sees significant benefits from enabling mixed precision training. Interestingly, though the V100 and T4 both benefit from mixed precision training, the benefit to the T4 is much greater: a 5% time save versus a whopping 30% time save.
  • BERT is a large model, and it’s where the time savings of using mixed precision training go from “nice” to “must-have”. Automatic mixed precision will cut training time for large models trained on Volta or Turing GPU by 50 to 60 percent! 🔥
  • This is a huge, huge benefit, especially when you take into account the minimal complexity required — just four or five LOC to your model training script.

Based on the aforementioned training time uplifts, ,ixed precision should be one of the first performance optimization you make to your model training scripts.

What about memory?

  • As explained in the section above on How mixed precision works, a fp16 matrix is half the size of a fp32 matrix in memory, so another purported advantage of mixed precision training is memory usage. GPU memory is much less of a bottleneck than GPU compute, but it’s still pretty valuable to optimize. The more efficient your memory usage, the larger the batch sizes you can fit on the GPU.

  • PyTorch reserves a certain amount of GPU memory at the beginning of the model training process and holds onto that memory for the duration of the training job. This keeps other processes from reserving too much GPU memory mid-training, forcing the PyTorch training script to crash with an OOM error.

  • Here is the impact that enabling mixed precision training has on the PyTorch memory reservation behavior:

  • Interestingly enough, while both of the larger models saw benefit from the swap to mixed precision, UNet benefited from the swap a lot more than BERT did. PyTorch memory allocation behavior is pretty opaque to me, so I have no insight into why this might be the case.

Conclusion

  • Automatic mixed precision training is an easy-to-use and powerful new feature which promises to speed up larger-scale model training jobs running on recent NVIDIA GPUs by up to 60%.
  • While this technique has been around for a while (see e.g. Chip Huyen’s notes on scaling) it’s not been very accessible to the average user because it’s never had a native PyTorch API — until now.
  • To learn more about mixed precision training directly from the source, see the automatic mixed precision package and automatic mixed precision examples pages in the PyTorch master docs.

Key takeways

  • The torch.cuda.amp mixed-precision training module delivers on its promise, delivering speed-ups of 50-60% in large model training jobs with just a handful of new lines of code.

Use-case

  • Automatic Mixed Precision (AMP)’s main goal is to reduce training time. (In contrast, as we saw in the section on Quantization, quantization’s main goal is to reduce inference time.)
  • Refer PyTorch Automatic Mixed Precision Recipe to learn hands-on usage.

Visual Summary

  • Credits for this section go to Damien Benveniste.
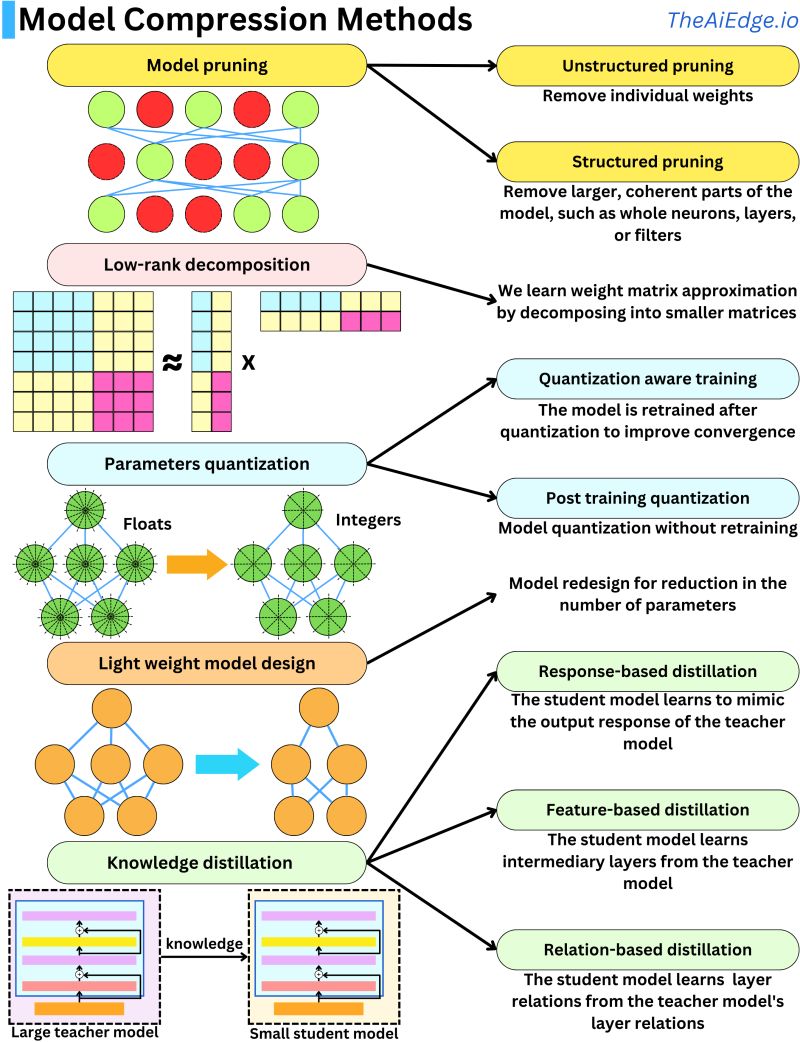
  • Not too long ago, the biggest Machine Learning models most people would deal with, merely reached a few GB in memory size. Now, every new generative model coming out is between 100B and 1T parameters! To get a sense of the scale, one float parameter that’s 32 bits or 4 bytes, so those new models scale between 400 GB to 4 TB in memory, each running on expensive hardware. Because of the massive scale increase, there has been quite a bit of research to reduce the model size while keeping performance up. There are 5 main techniques to compress the model size.
  • Model pruning is about removing unimportant weights from the network. The game is to understand what “important” means in that context. A typical approach is to measure the impact to the loss function of each weight. This can be done easily by looking at the gradient and second order derivative of the loss. Another way to do it is to use L1 or L2 regularization and get rid of the low magnitude weights. Removing whole neurons, layers or filters is called “structured pruning” and is more efficient when it comes to inference speed.
  • Model quantization is about decreasing parameter precision, typically by moving from float (32 bits) to integer (8 bits). That’s 4X model compression. Quantizing parameters tends to cause the model to deviate from its convergence point so it is typical to fine-tune it with additional training data to keep model performance high. We call this “Quantization aware training”. When we avoid this last step, it is called “Post training quantization”, and additional heuristic modifications to the weights can be performed to help performance.
  • Low-rank decomposition comes from the fact that neural network weight matrices can be approximated by products of low-dimension matrices. A \(N \times N\) matrix can be approximately decomposed into a product of \(2N \times 1\) matrices. That’s a \(O(N^2) -> O(N)\) space complexity gain!

  • Knowledge distillation is about transferring knowledge from one model to another. Typically from a large model to a smaller one. When the student model learns to produce similar output responses, that is response-based distillation. When the student model learns to reproduce similar intermediate layers, it is called feature-based distillation. When the student model learns to reproduce the interaction between layers, it is called relation-based distillation.

  • Lightweight model design is about using knowledge from empirical results to design more efficient architectures. That is probably one of the most used methods in LLM research.
  • The image below (source) does a great job illustrating some of the methods we will see further in the article.

Aside: Inference optimizations

  • A list of five techniques to optimize deep neural network model performance during inference.
    • Parallelization
    • Vectorization
    • Loop tiling
    • Operator fusion
    • Quantization
  • Note that these techniques don’t change the model architecture.
  • Credits to Sebastian Raschka for the infographic below.

On-Device Privacy

  • On-device privacy, also known as edge computing, involves processing data directly on a user’s device, such as a smartphone or tablet, instead of transferring it to a central server. This method offers a significant increase in privacy and security since user data never leaves the device, thus reducing the risk of exposure during transit or from a compromised server.
  • For NLP and LLM systems, on-device processing means all interactions, including the analysis and generation of responses, happen locally. It is especially important in conversational AI applications where private, personal conversations are common. On-device processing also reduces latency since data doesn’t need to travel over the network, thereby providing a smoother user experience.
  • However, the challenge lies in deploying these typically resource-intensive models to run efficiently on devices with limited computational capacity. Advances in model compression techniques, such as pruning and quantization, have made it increasingly possible to deploy smaller, yet effective models on device.

Differential Privacy

  • Differential privacy is a mathematical framework for quantifying the privacy of an individual in a dataset. The main idea is to add a certain amount of random noise to the data, making it statistically challenging to identify specific individuals while preserving the overall distribution and patterns in the dataset.
  • In the context of NLP and LLM, differential privacy ensures that the output of a model does not reveal sensitive information about the training data. For instance, if a language model is trained on a set of medical records, differential privacy will prevent the model from inadvertently generating text that could be traced back to a specific patient.
  • While the principle is robust, implementing differential privacy in complex models like LLMs is not straightforward. Striking the right balance between the level of noise (privacy) and the utility of the model is crucial.

Federated Learning

  • Federated learning is a machine learning approach that trains a model across multiple devices or servers while keeping data localized. Each device learns a local model that is periodically updated to a global model, but the raw data never leaves the original device.
  • In the world of NLP and conversational AI, federated learning allows models to learn from a diverse range of data sources without compromising privacy. For example, a conversational AI can learn from interactions on millions of devices, gaining the ability to understand a broad array of contexts, dialects, and colloquialisms, but it never sees the raw data of any specific conversation.
  • The challenge with federated learning lies in coordinating and aggregating the local model updates in an efficient and secure way. Also, issues like device availability, differing computational capacities, and network connectivity can affect the process.

Low-rank decomposition

  • Low-rank decomposition is based on the principle that the weight matrices within a neural network can be approximated by the multiplication of matrices with smaller dimensions.
  • In simpler terms, a matrix of size \(N \times N\) can be essentially broken down into the product of two matrices, each of size \(N \times 1\). This translates to a significant reduction in space complexity, specifically from quadratic (\(O(N^2)\)) to linear (\(O(N)\)), thereby enhancing computational efficiency significantly!

Further Reading

References

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledModelCompression,
  title   = {Model Compression},
  author  = {Chadha, Aman},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}