Background

  • Graph Neural Networks (GNNs) are rapidly advancing progress in ML for complex graph data applications. This primer presents a recipe for learning the fundamentals and staying up-to-date with GNNs.

  • GNNs are advanced neural network architectures designed to process graph-structured data, which are highly effective in various applications such as node classification, link prediction, and recommendation systems. GNNs can aggregate information from neighboring nodes and capture both local and global graph structures. They are particularly useful in recommender systems where they can process both explicit and implicit feedback from users, as well as contextual information. GNNs extend traditional neural networks to operate directly on graphs, a data structure capable of representing complex relationships.
  • A graph consists of sets of nodes or vertices connected by edges or links. In GNNs, nodes represent entities (like users or items), and edges signify their relationships or interactions.
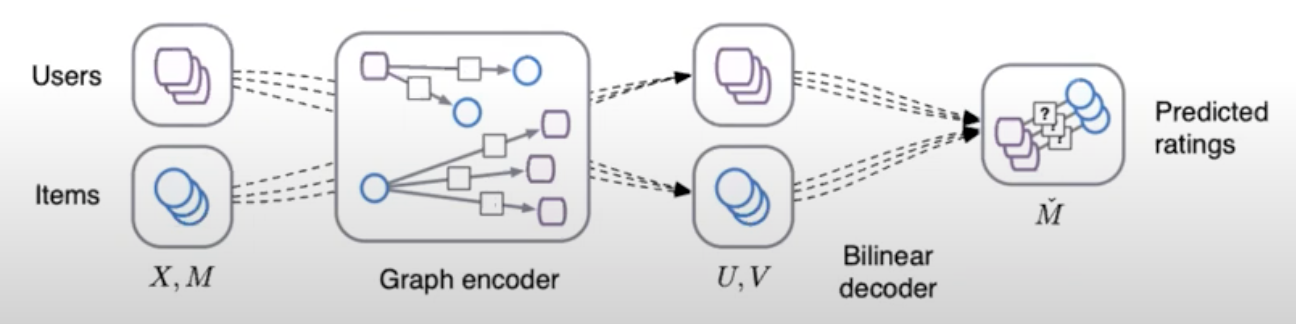
  • GNNs follow an encoder-decoder architecture. In the encoder phase, the graph is fed into the GNN, which computes a representation or embedding for each node, capturing both its features and context within the graph.
  • The decoder phase involves making predictions or recommendations based on the learned node embeddings, such as computing similarity measures between node pairs or using embeddings in downstream models.
  • GNNs can model complex relationships in recommender systems, including multimodal interactions or hierarchical structures, and can incorporate diverse data like time or location.
  • Generating embeddings in GNN-based recommender systems means representing user and item nodes as low-dimensional vectors, generally achieved through neural message passing.
  • Preference prediction is often done using measures like cosine similarity.
  • Popular GNN architectures include Graph Convolutional Networks (GCNs), Graph Attention Networks (GATs), GraphSAGE, and GGNNs. GNNs find use in several industry applications, notably in maps (Google/Uber) and social networks (LinkedIn, Instagram, Facebook). They leverage both content information (semantic) and the relationships between entities (structural), offering an advantage over traditional models that usually rely on just one type of information.
  • The image below (source) shows a high-level overview of how GNNs work for recommendation.

  • The image below (source) illustrates the different types of graphs, highlighting that recommender systems often follow a bipartite graph structure.

Key terms

  • Let’s start with learning the nomenclature associated with GNNs:
    • Homogeneous Graphs: This graph type has all the nodes and edges be of the same type. An example is a social network, where all the users are nodes and the edges are their friendships.
    • Heterogeneous Graphs: In contrast, this graph type has all the nodes and edges of different types with different representation of entities and relationships. An example is a recommendation system where users, movies, and genres are the entities, the graph would be considered heterogeneous because the nodes represent different types of objects (users, movies, genres) and the edges represent different types of relationships (user-movie interactions, movie-genre associations).
    • Node Embeddings: Node embeddings are low-dimensional vector representations that capture the structural and relational information of nodes in a graph. GNNs are designed to learn these embeddings by iteratively aggregating information from neighboring nodes.
    • Message Passing: Message passing is a fundamental operation in GNNs where nodes exchange information with their neighbors. During message passing, each node aggregates the information from its neighbors to update its own representation.
    • Aggregation Functions: Aggregation functions are used in GNNs to combine information from neighboring nodes. Common aggregation functions include summation, averaging, and max-pooling, among others. These functions determine how information is aggregated and propagated through the graph.
    • Graph Convolutional Networks (GCNs): GCNs are a popular type of GNN architecture that perform convolutional operations on graph-structured data. They adapt the concept of convolutions from traditional neural networks to the graph domain, enabling information propagation and feature extraction across the graph.
    • GraphSAGE: GraphSAGE (Graph Sample and Aggregation) is a GNN m odel that uses sampling techniques to efficiently learn node embeddings. It aggregates information from sampled neighborhood nodes to update a node’s representation. GraphSAGE is commonly used in large-scale graph applications.
    • Graph Attention Networks (GATs): GATs are GNN models that incorporate attention mechanisms. They assign attention weights to the neighboring nodes during message passing, allowing the model to focus on more relevant nodes and relationships.
    • Link Prediction: Link prediction is a task in GNNs that aims to predict the presence or absence of edges between nodes in a graph. GNNs can learn to model the likelihood of missing or future connections based on the graph’s structure and node features.
    • Graph Pooling: Graph pooling refers to the process of aggregating or downsampling nodes and edges in a graph to create a coarser representation. Pooling is often used in GNNs to handle graphs of varying sizes and reduce computational complexity.
    • Graph Classification: Graph classification involves assigning a label or category to an entire graph. GNNs can be trained to perform graph-level predictions by aggregating information from the nodes and edges in the graph.
    • Semi-Supervised Learning: GNNs often operate in a semi-supervised learning setting, where only a subset of nodes have labeled data. GNNs can leverage both labeled and unlabeled data to propagate information and make predictions on unlabeled nodes or graphs.
  • This section offers an overview of popular GNN architectures. For more details of their training process and their unique characteristics, please refer the GNNs for RecSys primer.

Graph Convolutional Networks

  • Graph Convolutional Networks (GCNs) are a type of neural network designed to work directly with graph-structured data. GCNs are particularly useful for several reasons:

    • Handling Sparse Data: Recommender systems often deal with sparse user-item interaction data. GCNs are adept at handling such sparse data by leveraging the graph structure.

    • Capturing Complex Relationships: GCNs can capture complex and non-linear relationships between users and items. In a typical recommender system graph, nodes represent users and items, and edges represent interactions (like ratings or purchases). GCNs can effectively learn these relationships.

    • Incorporating Side Information: GCNs can easily incorporate additional information (like user demographics or item descriptions) into the graph structure, providing a more holistic view of the user-item interactions.

Graph Attention Networks

  • Graph Attention Networks (GATs) are a type of neural network designed to operate on graph-structured data. They are particularly noteworthy for how they incorporate the attention mechanism, a concept widely used in fields like natural language processing, into graph neural networks.
  • Graph-based Framework: GATs are built for data represented in graph form. In a graph, data points (nodes) are connected by edges, which may represent various kinds of relationships or interactions.
  • Attention Mechanism: The key feature of GATs is the use of the attention mechanism to weigh the importance of nodes in a graph. This mechanism allows the model to focus more on certain nodes than others when processing the information, which is crucial for capturing the complexities of graph-structured data.

GraphSAGE

  • GraphSAGE (Graph Sample and Aggregated) is a GNN model introduced by Hamilton et al. in Inductive Representation Learning on Large Graphs. It aims to address the challenge of incorporating information from the entire neighborhood of a node in a scalable manner. The key idea behind GraphSAGE is to sample and aggregate features from a node’s local neighborhood to generate node representations.
  • In GraphSAGE, each node aggregates feature information from its immediate neighbors. This aggregation is performed in a message-passing manner, where each node gathers features from its neighbors, performs a pooling operation (e.g., mean or max pooling) to aggregate the features, and then updates its own representation using the aggregated information. This process is repeated iteratively for multiple layers, allowing nodes to incorporate information from increasing distances in the graph.
  • GraphSAGE utilizes the sampled and aggregated representations to learn node embeddings that capture both local and global graph information. These embeddings can then be used for various downstream tasks such as node classification or link prediction.

Edge GNN

  • Originally proposed in Exploiting Edge Features for Graph Neural Networks by Gong and Cheng from the University of Kentucky in CVPR 2019, Enhanced Graph Neural Network (EGNN) (or Edge GNN or Edge GraphSAGE) refers to an extension of the GraphSAGE model that incorporates information from both nodes and edges in the graph. While the original GraphSAGE focuses on aggregating information from neighboring nodes, Edge GNN takes into account the structural relationships between nodes provided by the edges.
  • In Edge GNN, the message-passing process considers both the features of neighboring nodes and the features of connecting edges. This allows the model to capture more fine-grained information about the relationships between nodes, such as the type or strength of the edge connection. By incorporating edge features in addition to node features, Edge GNN can learn more expressive representations that capture both node-level and edge-level information.
  • The Edge GNN model follows a similar iterative message-passing framework as GraphSAGE, where nodes gather and aggregate information from neighboring nodes and edges, update their representations, and propagate information across the graph. This enables the model to capture both semantic and structural information from both the local and global neighborhood of the graph and learn more comprehensive representations for nodes and edges.

Embedding Generation: Neural Message Passing

  • Generating embeddings in GNN is typically achieved through information propagation, also known as neural message passing, which involves passing information between neighboring nodes in the graph in a recursive manner, and updating the node representations based on the aggregated information.
  • The propagation process allows the embeddings to capture both local and global information about the nodes, and to incorporate the contextual information from their neighbors.
  • By generating informative and expressive embeddings, GNN-based recommenders can effectively capture the complex user-item interactions and item-item relations, and make accurate and relevant recommendations.
  • Neural message passing is a key technique for generating embeddings in GNN-based recommender systems. It allows the nodes in the graph to communicate with each other by passing messages along the edges, and updates their embeddings based on the aggregated information.
  • At a high level, the message passing process consists of two steps:
    1. Message computation: In this step, each node sends a message to its neighboring nodes, which is typically computed as a function of the node’s own embedding and the embeddings of its neighbors. The message function can be a simple linear transformation, or a more complex non-linear function such as a neural network.
    2. Message aggregation: In this step, each node collects the messages from its neighbors and aggregates them to obtain a new representation of itself. The aggregation function can also be a simple sum or mean, or a more complex function such as a max-pooling or attention mechanism.
  • The message passing process is usually performed recursively for a fixed number of iterations, allowing the nodes to exchange information with their neighbors and update their embeddings accordingly. The resulting embeddings capture the local and global information about the nodes, as well as the contextual information from their neighbors, which is useful for making accurate and relevant recommendations.
  • Some common algorithms and techniques used for neural message passing in GNNs are:
    • Graph Convolutional Networks (GCNs): GCNs apply a localized convolution operation to each node in the graph, taking into account the features of its neighboring nodes. This allows for the aggregation of information from neighboring nodes to update the node’s feature representation.
    • Graph Attention Networks (GATs): GATs use a learnable attention mechanism to weigh the importance of neighboring nodes when updating a node’s feature representation. This allows the model to selectively focus on the most relevant neighbors.
    • GraphSAGE: GraphSAGE uses a hierarchical sampling scheme to aggregate information from the neighborhood of each node. This allows for efficient computation of node embeddings for large graphs.
    • Message Passing Neural Networks (MPNNs): MPNNs use a general framework for message passing between nodes in a graph, allowing for flexibility in modeling different types of interactions.
  • In the context of GNNs for recommender systems, the goal is to generate embeddings for the user and item nodes in the graph. The embeddings can then be used for tasks such as candidate generation, scoring, and ranking.
  • The process of generating embeddings involves multiple GNN layers, each of which performs an exchange of information between the immediate neighbors in the graph. At each layer, the information exchanged is aggregated and processed to generate new embeddings for each node. This process can be repeated for as many layers as desired, and the number of layers determines how far information is propagated in the graph.
  • For example, in a 2-layer GNN model, each node will receive information from its immediate neighbors (i.e., nodes connected by an edge) and its immediate neighbors’ neighbors. This allows information to be propagated beyond a node’s direct neighbors, potentially capturing higher-level structural relationships in the graph.
  • From Building a Recommender System Using Graph Neural Networks, here is the pseudo-code for generating embeddings for a given node:
    1. Fetch incoming messages from all neighbors.
    2. Reduce all those messages into 1 message by doing mean aggregation.
    3. Matrix multiplication of the neighborhood message with a learnable weight matrix.
    4. Matrix multiplication of the initial node message with a learnable weight matrix.
    5. Sum up the results from steps 3 and 4.
    6. Pass the sum through a ReLU activation function to model non-linearity relationships in the data.
    7. Repeat for as many layers as desired. The result is the output of the last layer.
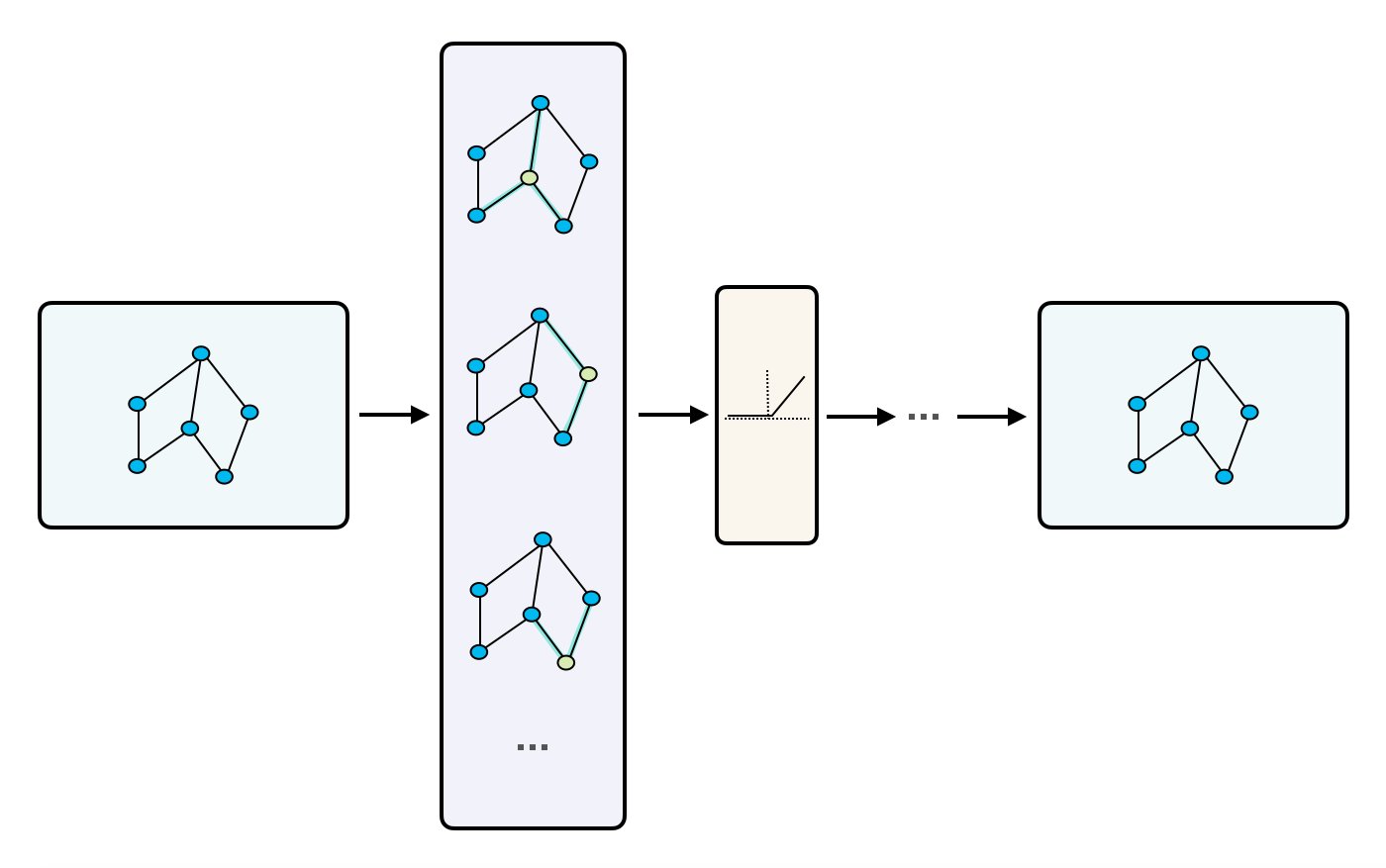
  • The image below (source) visually represents this pseudo code.

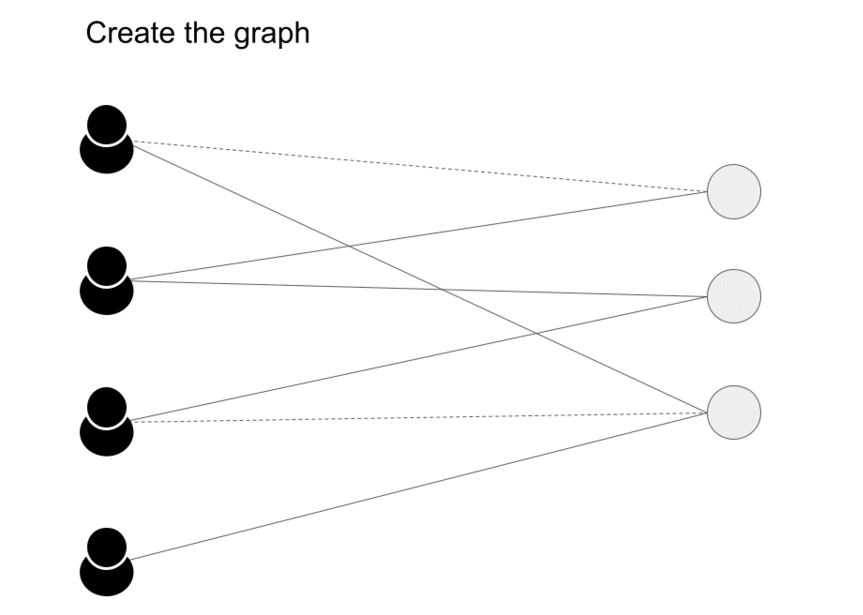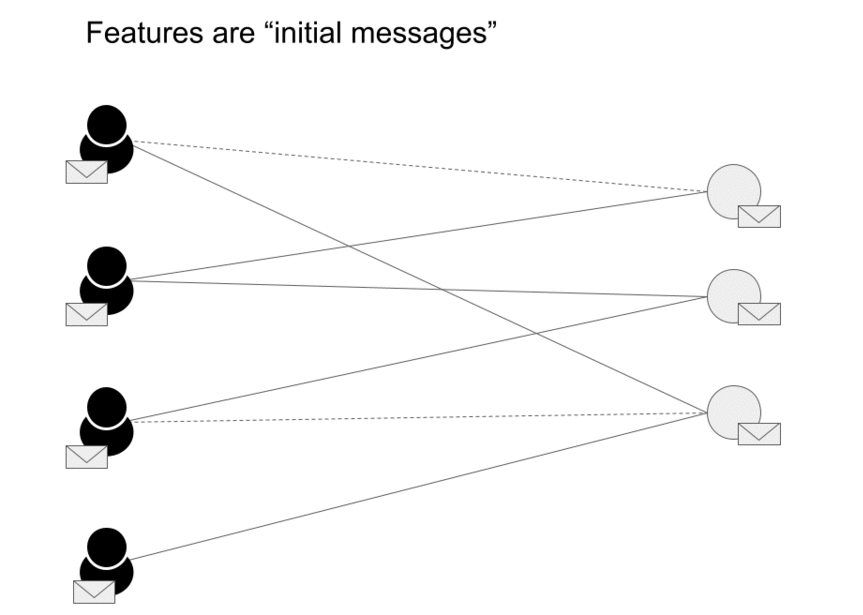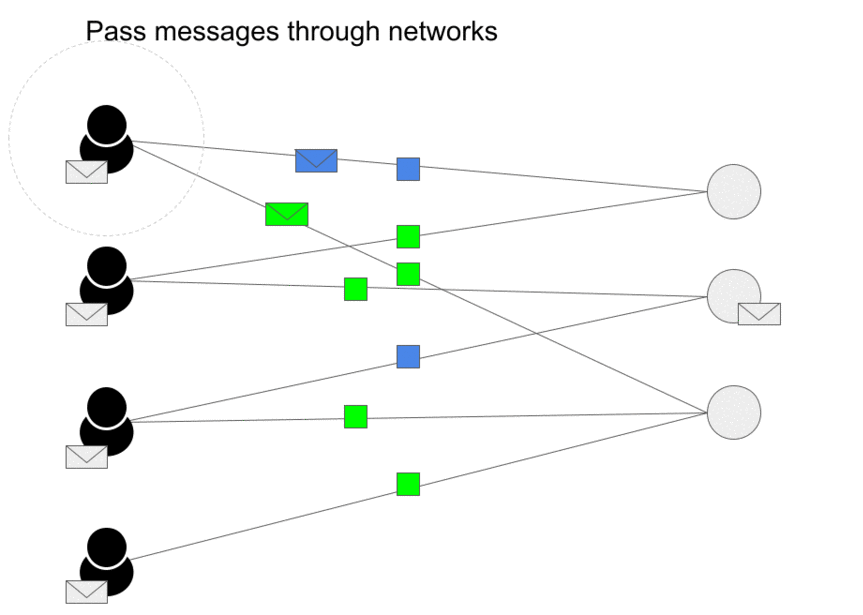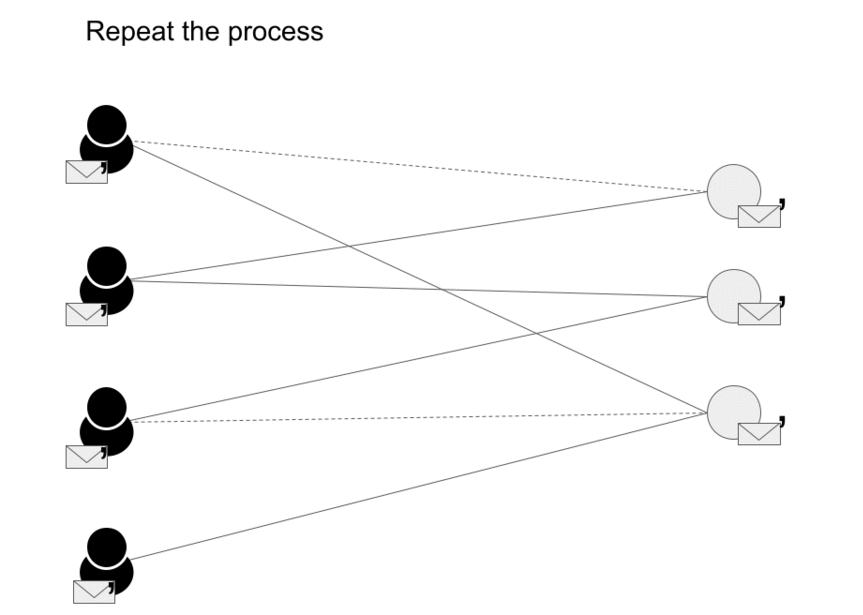
  • Message passing has two steps, Aggregation and Update as we can see in the image (source) below.

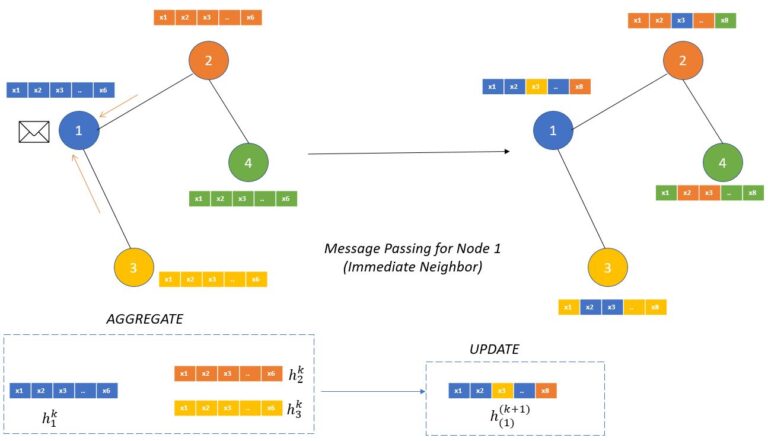
  • The aggregation function works on defining how the messages from the neighboring nodes are combined to compute new representations of the node.
  • “This aggregate function should be a permutation invariant function like sum or average. The update function itself can be a neural network (with attention or without attention mechanism) which will generate the updated node embeddings.” (source)

Benefits of GNNs

  • Incorporating Graph Structure: GNNs are designed to process data with inherent graph structure, which is particularly useful in recommender systems. Recommender systems often involve modeling relationships between users, items, and their interactions. GNNs can effectively capture these complex relationships and dependencies by leveraging the graph structure, leading to more accurate and personalized recommendations.
  • Implicit Collaborative Filtering: Collaborative filtering is a popular recommendation technique that relies on user-item interactions. GNNs can handle implicit feedback data, such as user clicks, views, or purchase history, without the need for explicit ratings. GNNs can learn from the graph connections and propagate information across users and items, enabling collaborative filtering in a more efficient and scalable manner.
  • Modeling User and Item Features: GNNs can handle heterogeneous data by incorporating user and item features alongside the graph structure. In recommender systems, users and items often have associated attributes or contextual information that can influence the recommendations. GNNs can effectively integrate these features into the learning process, allowing for more personalized recommendations that consider both user preferences and item characteristics.
  • Capturing Higher-Order Dependencies: GNNs can capture higher-order dependencies by aggregating information from neighboring nodes in multiple hops. This allows GNNs to capture complex patterns and relationships that may not be easily captured by traditional recommendation algorithms. GNNs can discover latent factors and capture long-range dependencies, resulting in improved recommendation quality.
  • Cold Start Problem: GNNs can help address the cold start problem, which occurs when there is limited or no historical data for new users or items. By leveraging the graph structure and user/item features, GNNs can generalize from existing data and make reasonable recommendations even for users or items with limited interactions.
  • Interpretability: GNNs provide interpretability by allowing inspection of the learned representations and the influence of different nodes or edges in the graph. This can help understand the reasoning behind recommendations and provide transparency to users, increasing their trust in the system.

Loss functions

  • Binary Cross-Entropy Loss: Binary cross-entropy loss is often used for binary classification tasks in GNNs. It is suitable when the task involves predicting a binary label or making a binary decision based on the graph structure and node features.
  • Categorical Cross-Entropy Loss: Categorical cross-entropy loss is used for multi-class classification tasks in GNNs. If the GNN is trained to predict the class label of nodes or edges in a graph, this loss function is commonly employed.
  • Mean Squared Error (MSE) Loss: MSE loss is frequently used for regression tasks in GNNs. If the goal is to predict a continuous or numerical value associated with nodes or edges in the graph, MSE loss can measure the difference between predicted and true values.
  • Pairwise Ranking Loss: Pairwise ranking loss is suitable for recommendation or ranking tasks in GNNs. It is used when the goal is to learn to rank items or nodes based on their relevance or preference to users. Examples of pairwise ranking loss functions include the hinge loss and the pairwise logistic loss.
  • Triplet Ranking Loss: Triplet ranking loss is another type of loss function used for ranking tasks in GNNs. It aims to learn representations that satisfy certain constraints among a triplet of samples. The loss encourages the model to assign higher rankings to relevant items compared to irrelevant items.
  • Graph Reconstruction Loss: Graph reconstruction loss is employed when the goal is to reconstruct the input graph or its properties using the GNN. This loss compares the reconstructed graph with the original graph to measure the similarity or reconstruction error.

GNNs in NLP

  • GNNs are a type of Neural Network that operate on data structured as graphs. They can capture the complex relationships between nodes in a graph, which can often provide more nuanced representations of the data than traditional neural networks.
  • While GNNs are often used in areas like social network analysis, citation networks, and molecular chemistry, they’re also finding increasing use in the field of Natural Language Processing (NLP).
  • One of the main ways GNNs are used in NLP is in capturing the dependencies and relations between words in a sentence or phrases in a text. For example, a text can be represented as a graph where each word is a node and the dependencies between them are edges. GNNs can then learn representations for the words in a way that takes into account both the words’ individual properties and their relations to other words.
  • One specific use case is in the field of Information Extraction, where GNNs can help determine relations between entities in a text. They can also be used in semantic role labeling, where the aim is to understand the semantic relationships between the words in a sentence.
  • The fundamental principle behind GNNs is the neighborhood aggregation or message-passing framework. The representation of a node in a graph is computed by aggregating the features of its neighboring nodes. The most basic form of GNN - Graph Convolutional Network (GCN) operates in the following way:
    1. Node-level Feature Aggregation:
      • For each node \(v\) in the graph, we aggregate the feature vectors of its neighboring nodes. This can be a simple average: \(h_{v}^{(1)} = \frac{1}{|\mathcal{N}(v)|} \sum_{u \in \mathcal{N}(v)} x_u\)
        • where \(h_{v}^{(1)}\) is the first-level feature of node \(v\), \(x_u\) is the input feature of node \(u\), and \(\|\mathcal{N}(v)\|\) denotes the number of neighbors of \(v\).
    2. Feature Transformation:
      • Then, a linear transformation followed by a non-linear activation function is applied to these aggregated features: \(h_{v}^{(2)} = \sigma(W h_{v}^{(1)})\)
        • where \(h_{v}^{(2)}\) is the second-level feature of node \(v\), \(W\) is a learnable weight matrix, and \(\sigma\) denotes a non-linear activation function such as ReLU.

Loss Functions

  • The choice of loss function in training GNNs depends on the specific task at hand.
  • For example, in a classification task (like sentiment analysis), you might use a cross-entropy loss, which measures the dissimilarity between the predicted probability distribution and the true distribution.
  • In a sequence labeling task (like named entity recognition or part-of-speech tagging), you might use a sequence loss like the conditional random field (CRF) loss.
  • In a regression task (like predicting the semantic similarity between two sentences), you might use a mean squared error loss.
  • It’s also common to use a combination of different loss functions. For example, you might use a combination of cross-entropy loss for classification and a regularization term to prevent overfitting.
  • In all cases, the goal of the loss function is to provide a measure of how well the network’s predictions align with the true labels in the training data, and to guide the adjustment of the network’s weights during training.

  • The choice of loss function for GNNs in NLP tasks greatly depends on the specific problem being addressed.

  • Classification Task: For a multi-class classification task, Cross-Entropy loss is commonly used. The cross-entropy loss for a single data point can be calculated as:

    \[L = -\sum_{c=1}^{M} y_{o,c} \log(p_{o,c})\]
    • where \(y\) is a binary indicator (0 or 1) if class label \(c\) is the correct classification for observation \(o\), and \(p\) is the predicted probability observation \(o\) is of class \(c\).

  • Sequence Labeling Task: For tasks like named entity recognition or part-of-speech tagging, Conditional Random Field (CRF) loss can be used. This loss is more complicated and beyond the scope of this brief explanation, but essentially it learns to predict sequences of labels that take into account not just individual label scores, but also their relationships to each other.

  • Regression Task: For predicting continuous values, Mean Squared Error (MSE) loss is commonly used. The MSE loss can be calculated as:

    \[L = \frac{1}{n}\sum_{i=1}^{n}(Y_i - \hat{Y_i})^2\]
    • where \(Y\) is the ground truth value, \(Ŷ\) is the predicted value, and \(n\) is the total number of data points.
  • It’s important to note that these are just typical examples. The choice of loss function should always be tailored to the specific task and the data at hand.

Walkthrough

  • Now, let’s do a quick walkthrough on creating our own system from scratch and see all the steps that it would take.
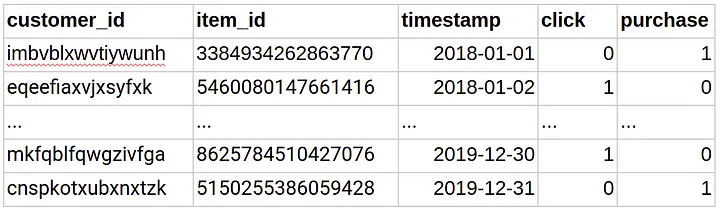
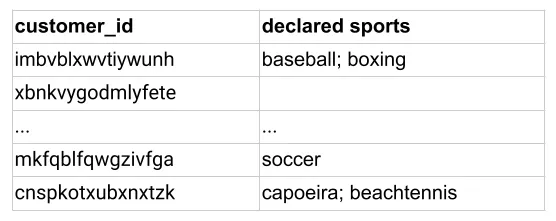
  • First is the dataset, say we have user-item interaction, item features and user features available as shown below (source) starting with user-item interaction.

  • The item features are as below.

  • The user features are as below.

  • The next step is to create a graph as shown below (source).

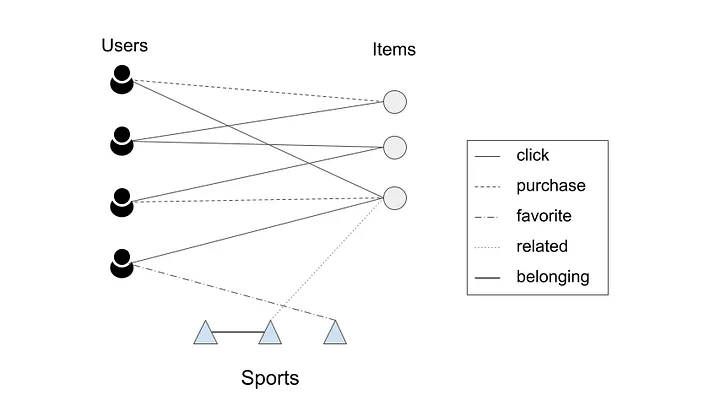
  • The embeddings are created using the procedure elaborated in Embedding Generation: Neural Message Passing. The embeddings generated by GNNs are utilized to estimate the likelihood of a connection between two nodes. To calculate the probability of interaction between a user \(u\) and an item \(v\), we use the cosine similarity function. After computing scores for all items that a user did not interact with, the system recommends the items with the highest scores.
  • The main goal during training of the model is to optimize the trainable matrices (\(W\)) used for generating the embeddings. To achieve this, a max-margin loss function is used, which involves negative sampling. The training data set only includes edges representing click and purchase events.
  • The model is trained in such a way that it learns to predict a higher score for a positive edge (an edge between a user and an item that they actually interacted with) compared to randomly sampled negative edges. These negative edges are connections between a user and random items that they did not interact with. The idea is to teach the model to distinguish between actual positive interactions and randomly generated negative interactions.

FAQs

What is the degree of a node?

  • The degree of a node in a graph is the number of edges connected to that node. It indicates how many direct connections (or neighbors) the node has within the graph. Depending on the type of graph, the degree can be defined differently:

Undirected Graphs

  • In an undirected graph, where edges do not have a direction, the degree of a node is simply the total number of edges incident to that node.
  • For example, if a node has 3 edges connected to it, the degree of the node is 3.

Directed Graphs

  • In a directed graph, where edges have a direction (from one node to another), the degree of a node can be divided into two types:
    • In-degree: The number of edges directed toward the node (i.e., how many edges end at the node).
    • Out-degree: The number of edges directed away from the node (i.e., how many edges start from the node).
  • The total degree of a node in a directed graph can be considered as the sum of its in-degree and out-degree.

Examples

  1. Undirected Graph: 
    A -- B -- C
     |
     D
    • Node A has 1 edge, so its degree is 1.
    • Node B has 3 edges, so its degree is 3.
    • Node C has 1 edge, so its degree is 1.
    • Node D has 1 edge, so its degree is 1.
  2. Directed Graph: 
    A → B ← C
     ↓
     D
    • Node A has an out-degree of 1 (edge from A to B) and in-degree of 0, so its total degree is 1.
    • Node B has an in-degree of 2 (edges from A and C) and out-degree of 1 (edge to D), so its total degree is 3.
    • Node C has an out-degree of 1 (edge to B) and in-degree of 0, so its total degree is 1.
    • Node D has an in-degree of 1 (edge from B) and out-degree of 0, so its total degree is 1.

In summary

  • Degree of a node (in undirected graphs) = Number of edges connected to it.
  • In-degree (in directed graphs) = Number of edges coming into the node.
  • Out-degree (in directed graphs) = Number of edges going out from the node.

How does a GNN produces node embeddings?

  • GNNs generate node embeddings by leveraging both the features of individual nodes and the structural information of the graph. The basic idea is to learn representations (embeddings) for nodes by aggregating information from their neighbors iteratively. Here’s an overview of how GNNs produce node embeddings.

Input: Graph Structure and Node Features

  • A graph is represented by a set of nodes \(V\) and edges \(E\), typically denoted as \(G = (V, E)\).
  • Each node \(v \in V\) may have associated feature vectors \(h_v^{(0)}\), which represent the initial node features. These could be properties like a node’s degree, label, or any domain-specific attributes.

Neighborhood Aggregation: Message Passing Framework

  • The core process of GNNs relies on the message-passing or neighborhood aggregation mechanism. In each layer, every node gathers and aggregates information from its neighbors to update its representation. This is done iteratively, layer by layer.

  • Message Passing: At each layer \(l\), the GNN computes a new representation (embedding) for node \(v\) based on its current representation \(h_v^{(l)}\) and the representations of its neighbors. The message-passing step can be written as: \(m_v^{(l+1)} = \text{AGGREGATE} \left( \{ h_u^{(l)} : u \in \mathcal{N}(v) \} \right)\)
    • where, \(\mathcal{N}(v)\) represents the neighbors of node \(v\), and the AGGREGATE function defines how information from neighbors is combined (e.g., summing, averaging, or using more complex functions like attention).
  • Update: After aggregation, each node updates its own embedding using a combination of its previous embedding and the aggregated messages: \(h_v^{(l+1)} = \text{UPDATE} \left( h_v^{(l)}, m_v^{(l+1)} \right)\)

    • This can be a simple neural network layer (like a fully connected layer) that processes the aggregated information.

    • For example, in a simple Graph Convolutional Network (GCN), the update step may look like: \(h_v^{(l+1)} = \sigma \left( W^{(l)} \cdot \sum_{u \in \mathcal{N}(v)} \frac{1}{\sqrt{d_v d_u}} h_u^{(l)} \right)\)

      • where, \(W^{(l)}\) is a trainable weight matrix for layer \(l\), \(d_v\) and \(d_u\) are the degrees of nodes \(v\) and \(u\), and \(\sigma\) is an activation function like ReLU.

Stacking Layers for Higher-Order Neighborhood Information

  • GNNs typically stack multiple layers, where each layer aggregates information from progressively larger neighborhoods.

    • In the first layer, each node aggregates information from its immediate neighbors.
    • In the second layer, each node aggregates information from its neighbors’ neighbors, and so on.

    After \(L\) layers, each node’s embedding will contain information from all nodes within \(L\) hops in the graph. Thus, the deeper the GNN, the more global the information a node embedding can capture, although very deep GNNs can suffer from over-smoothing, where the embeddings of nodes in large neighborhoods become indistinguishable.

Output: Node Embeddings

  • After passing through several layers of the GNN, each node \(v\) will have an embedding \(h_v^{(L)}\), where \(L\) is the number of layers. This final embedding can be used for various downstream tasks like:

    • Node classification: The embedding is passed through a final classifier to predict a label for each node.
    • Link prediction: The embeddings of two nodes are combined to predict the likelihood of an edge between them.
    • Graph-level tasks: Node embeddings can be pooled (aggregated) to create a graph embedding, useful for graph classification tasks.

Types of GNN Architectures

  • There are several popular GNN architectures that follow this general process but differ in how they implement the aggregation and update steps:

    • Graph Convolutional Networks (GCNs): Aggregate neighbor information by averaging it.
    • GraphSAGE: Aggregates using mean, max-pooling, or LSTMs and allows for inductive learning (generalizing to unseen nodes/graphs).
    • Graph Attention Networks (GATs): Use attention mechanisms to assign different importance (weights) to neighbors during aggregation.
    • Message Passing Neural Networks (MPNNs): A general framework for GNNs where message-passing functions and update functions are flexible.

Summary

  • Node features and graph structure (edges) are the inputs.
  • Each node iteratively aggregates information from its neighbors using a message-passing framework.
  • After several layers of aggregation, each node’s embedding contains information from its local neighborhood.
  • These embeddings are learned in a way that reflects both the node features and the graph topology, making them useful for tasks like node classification, link prediction, and graph-level tasks.

How do various GNN architectures (GCNs, GraphSAGE, GATs, MPNNs, etc.) differ in terms of their aggregate and update step for producing node embeddings?

  • Different Graph Neural Network (GNN) architectures differ in how they perform the aggregate and update step. The core idea in each of them is to combine (or aggregate) information from a node’s neighbors and then update the node’s embedding. However, the specifics of how they carry out this update vary depending on the architecture. Here’s a detailed comparison.

Graph Convolutional Networks (GCNs)

  • Aggregation: GCNs aggregate neighbor information by averaging (weighted by node degree for normalization) the features of the neighbors.

  • Update Step: After aggregation, GCNs update the node embeddings by applying a linear transformation (learned weight matrix) followed by a non-linear activation function (like ReLU). Mathematically, this can be written as:

    \[h_v^{(l+1)} = \sigma \left( W^{(l)} \cdot \sum_{u \in \mathcal{N}(v)} \frac{1}{\sqrt{d_v d_u}} h_u^{(l)} \right)\]
    • where:
      • \(h_v^{(l+1)}\) is the updated embedding of node \(v\) at layer \(l+1\).
      • \(W^{(l)}\) is the learnable weight matrix for layer \(l\).
      • \(\sigma\) is a non-linear activation (e.g., ReLU).
      • \(\mathcal{N}(v)\) represents the neighbors of node \(v\).
      • \(d_v\) and \(d_u\) are the degrees of nodes \(v\) and \(u\), respectively (used for normalization).
  • In GCNs, the update step is fairly straightforward: aggregate, normalize, apply a linear transformation, and pass through an activation function.

GraphSAGE

  • Aggregation: GraphSAGE aggregates neighbor information using different possible functions like:
  • Mean aggregation: Similar to GCN, the mean of the neighbors’ features is taken.
  • Max-pooling aggregation: Applies a pooling operation (e.g., taking the maximum value across features).
  • LSTM-based aggregation: Uses a Long Short-Term Memory (LSTM) network to aggregate the neighbors’ features.
  • Update Step: After aggregation, GraphSAGE updates the node embeddings by concatenating the node’s own current embedding with the aggregated information from its neighbors. This concatenated vector is then passed through a fully connected layer to update the node embedding: \(h_v^{(l+1)} = \sigma \left( W^{(l)} \cdot \text{CONCAT}(h_v^{(l)}, \text{AGGREGATE}(\{ h_u^{(l)} : u \in \mathcal{N}(v) \})) \right)\)
    • where, the concatenation of the node’s own embedding \(h_v^{(l)}\) with the aggregated neighbor information helps retain both the node’s original features and its local neighborhood context.

GraphSAGE differs from GCN by using more flexible aggregation strategies and by concatenating the node’s current embedding with the neighborhood’s aggregated information.

Graph Attention Networks (GATs)

  • Aggregation: GATs introduce an attention mechanism to aggregate neighbor information. Instead of treating all neighbors equally (like GCN), GATs assign different weights (attention scores) to different neighbors based on their relative importance. The attention score \(\alpha_{vu}\) between nodes \(v\) and \(u\) is learned using a feedforward neural network and normalized using the softmax function: \(\alpha_{vu} = \text{softmax}_u \left( \text{LeakyReLU} \left( a^T [W^{(l)} h_v^{(l)} || W^{(l)} h_u^{(l)}] \right) \right)\)
    • where:
      • \(a\) is a learnable vector.
      • $$   $$ denotes concatenation.

  • Update Step: After calculating the attention scores \(\alpha_{vu}\), GATs compute a weighted sum of the neighbors’ features based on these attention scores. The node embedding is then updated as follows: \(h_v^{(l+1)} = \sigma \left( \sum_{u \in \mathcal{N}(v)} \alpha_{vu} W^{(l)} h_u^{(l)} \right)\)

  • In GATs, the update step relies heavily on the attention mechanism, which dynamically adjusts the importance of each neighbor during aggregation.
  • GATs differ significantly from GCNs and GraphSAGE by learning a weighting mechanism (attention) that dictates how much influence each neighbor has on a node’s updated embedding.

Message Passing Neural Networks (MPNNs)

  • Aggregation: MPNNs provide a general framework for message passing in GNNs. The aggregation step in MPNNs can be highly flexible and depends on the specific design of the message-passing function. In general, each node receives a “message” from its neighbors based on their embeddings and any associated edge features: \(m_v^{(l+1)} = \sum_{u \in \mathcal{N}(v)} \text{MESSAGE}(h_v^{(l)}, h_u^{(l)}, e_{vu})\)
    • where, \(e_{vu}\) represents any features associated with the edge between nodes \(v\) and \(u\).
  • Update Step: The node embedding is updated by applying an update function (like a GRU, LSTM, or a simple neural network layer) to the aggregated message:
\[h_v^{(l+1)} = \text{UPDATE}(h_v^{(l)}, m_v^{(l+1)})\]
  • The update step in MPNNs is highly customizable and can involve various functions such as gated recurrent units (GRU), LSTM, or even a simple fully connected layer. This allows MPNNs to handle different types of tasks and graph structures.
  • The key difference in MPNNs is that both the message-passing function and the update function are flexible and can be designed in various ways, allowing for more expressive modeling compared to GCN, GraphSAGE, and GAT.

Summary of Differences in the Update Step

  • GCNs: Update by applying a linear transformation (weight matrix) and non-linearity after averaging neighbor features (with normalization).
  • GraphSAGE: Update by concatenating the node’s own embedding with the aggregated neighbor features (using mean, max-pooling, or LSTM) and passing through a fully connected layer.
  • GATs: Update by calculating attention scores to weight the neighbors’ features before applying a linear transformation and non-linearity.
  • MPNNs: Update via a flexible update function (such as GRU, LSTM, or a neural network layer) applied to aggregated messages from neighbors, with customizable message-passing mechanisms.
  • Each architecture has its strengths and trade-offs depending on the type of graph data and the task at hand.

in a GNN, how are embeddings of edges used while producing node embeddings?

  • In a Graph Neural Network (GNN), edge embeddings can play a crucial role in enhancing the representation of the relationships between nodes when producing node embeddings. While traditional GNNs like Graph Convolutional Networks (GCNs) primarily focus on node features and graph structure (edges treated as unweighted connections), many advanced GNN models incorporate edge features or edge embeddings into the message-passing and aggregation process.
  • Here’s how edge embeddings are typically used while producing node embeddings.

Edge Features in Message Passing

  • Many GNN architectures extend the basic message-passing framework to include edge features or edge embeddings. In these cases, the message from one node to another is influenced not only by the source node’s features but also by the features of the edge connecting them.
  • The message-passing function in a GNN that uses edge features or edge embeddings typically takes the following form: \(m_{v \to u}^{(l)} = \text{MESSAGE}(h_v^{(l)}, h_u^{(l)}, e_{vu})\)
    • where:
      • \(h_v^{(l)}\) is the embedding of node \(v\) at layer \(l\),
      • \(h_u^{(l)}\) is the embedding of node \(u\) at layer \(l\),
      • \(e_{vu}\) is the embedding or feature vector of the edge between nodes \(v\) and \(u\).
  • The message is computed using both the node features and the edge features, where the edge feature provides additional context about the relationship between the two nodes.
  • Example: If the edge represents a physical connection between two devices (nodes), the edge feature might represent bandwidth or latency. This additional information can modify how much or in what way the node aggregates messages from its neighbors.

Aggregation of Edge-Weighted Messages

  • Once messages have been calculated for each edge connected to a node, these messages are aggregated (summed, averaged, max-pooled, or passed through an attention mechanism). The edge embeddings influence how much weight or importance a particular neighbor’s message has during aggregation. For example: \(h_u^{(l+1)} = \text{AGGREGATE} \left( \{ \text{MESSAGE}(h_v^{(l)}, h_u^{(l)}, e_{vu}) : v \in \mathcal{N}(u) \} \right)\)

  • In this aggregation step, the edge features \(e_{vu}\) affect how the node \(u\) updates its own embedding based on the messages from its neighbors \(v\).

Edge Embeddings in Specific GNN Architectures

Message Passing Neural Networks (MPNNs)

  • MPNNs explicitly allow for edge embeddings during message passing. The message-passing function in MPNNs includes edge features, which are incorporated as follows: \(m_{v \to u}^{(l)} = f(h_v^{(l)}, h_u^{(l)}, e_{vu})\)
    • where, the function \(f\) can be a neural network or another learnable function that combines the node embeddings and edge embeddings. The edge features are treated as part of the input to compute the message, influencing how much of node \(v\)’s information gets passed to node \(u\).

Graph Attention Networks (GATs) with Edge Features

  • GATs use an attention mechanism to compute how much attention a node should pay to each of its neighbors. In cases where edge features are present, these can be incorporated into the attention score calculation. The attention mechanism might look like this: \(\alpha_{vu} = \text{softmax}_u \left( \text{LeakyReLU}(a^T [W^{(l)} h_v^{(l)} || W^{(l)} h_u^{(l)} || e_{vu}]) \right)\)
    • where, the edge embedding \(e_{vu}\) is concatenated with the node features and used to compute the attention score \(\alpha_{vu}\). This allows the model to learn different levels of importance based on the edge characteristics.

Edge-Conditioned Convolution (ECC)

  • In the Edge-Conditioned Convolution (ECC) variant of GNNs, the edge features are used to modulate the weights of the convolutional filters dynamically. The weight matrix \(W_{vu}\) used in the aggregation process is a function of the edge feature \(e_{vu}\): \(W_{vu} = g(e_{vu}; \theta)\)
    • where, \(g\) is a learnable function (like a neural network) that generates the weights based on the edge embedding \(e_{vu}\). The edge features directly influence how messages are propagated and aggregated across the graph.
  • For tasks like link prediction, edge embeddings are critical because the model needs to predict the likelihood of an edge existing between two nodes. In such cases, edge embeddings (or learned edge features) can be used to represent relationships between pairs of nodes, based on their node embeddings. The final edge prediction might involve combining the node embeddings and edge embeddings as follows: \(e_{vu} = f(h_v^{(L)}, h_u^{(L)}, e_{vu})\)
    • where, \(f\) is a function that scores the likelihood of an edge between nodes \(v\) and \(u\) given their embeddings and any associated edge features.

General Update with Edge Embeddings

  • In GNNs that use edge embeddings, the general update step (after aggregation) can be summarized as: \(h_u^{(l+1)} = \text{UPDATE} \left( h_u^{(l)}, \sum_{v \in \mathcal{N}(u)} \text{MESSAGE}(h_v^{(l)}, h_u^{(l)}, e_{vu}) \right)\)
  • In this process:
    • The message-passing function computes a message for each edge, taking into account the edge embedding.
    • The messages from all neighbors are aggregated to create a single vector representing the influence of the neighborhood.
    • The node embedding is then updated using this aggregated information.

Edge Embeddings in Heterogeneous Graphs

  • In heterogeneous graphs, where edges can represent different types of relationships, edge embeddings can represent these different types. For instance, in a social network, an edge might represent a friendship, a colleague relationship, or a family relationship. The edge embeddings encode the type of connection, allowing the GNN to process different edge types in a differentiated manner.

Summary

  • Edge embeddings provide additional information about the relationships between nodes and are often incorporated into the message-passing function in GNNs.
  • They influence how much and in what way nodes aggregate messages from their neighbors.
  • Edge embeddings can be used to modulate the weights in aggregation or can be directly combined with node embeddings in architectures like MPNNs and ECC.
  • In attention-based GNNs like GATs, edge embeddings can help determine how much attention a node pays to each neighbor.
  • By incorporating edge features, GNNs can better capture the rich semantics of graph relationships, improving their ability to represent and predict complex systems.

Further Reading

Introductory Content

Survey Papers on GNNs

Diving Deep into GNNs

GNN Papers and Implementations

  • If you want to keep up-to-date with popular recent methods and paper implementations for GNNs, the Papers with Code community maintains this useful collection:

Benchmarks and Datasets

Tools

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledGraphNeuralNetworks,
  title   = {Graph Neural Networks},
  author  = {Chadha, Aman and Jain, Vinija},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}