Models • Gemma 3n
- Overview
- Key Architectural Innovations
- Model Components and Structure
- Performance and Deployment
- References
- Citation
Overview
- Unveiled at Google I/O 2025, Gemma 3n is Google’s latest open-weight, multimodal AI model, engineered for efficient on-device performance across a wide range of platforms, including smartphones, tablets, and laptops.
- Gemma 3n builds upon the success of earlier Gemma models and integrates several groundbreaking architectural innovations that target efficient execution in resource-constrained environments. These include Per-Layer Embeddings (PLE), the MatFormer architecture, Conditional Parameter Loading, Learned Augmented Residual Layer (LAuReL), and Alternating Updates (AltUp).
- Designed natively for multimodal applications, Gemma 3n supports text, image, audio, and video inputs, while producing coherent and high-quality text outputs.
- With a strong developer-first approach, Gemma 3n is compatible with popular toolchains such as Hugging Face Transformers,
llama.cpp, Ollama, MLX, Google AI Edge, and more. It supports seamless deployment via platforms like Google AI Studio, Docker, and Cloud Run, and is integrated with tooling from AMD, NVIDIA, RedHat, and the broader open-source community. - Two effective model sizes are offered: E2B (~2B effective parameters) and E4B (~4B effective parameters), derived from base models with raw parameter counts as 5B and 8B respectively. Through architectural optimizations such as PLE caching and MatFormer nesting, these models achieve inference speeds and memory profiles equivalent to much smaller models, with E2B capable of running with as little as 2GB of RAM and E4B with just 3GB.
- Quality benchmarks indicate that Gemma 3n E4B exceeds 1300 on the LMArena benchmark, making it the first sub-10B parameter model to surpass this threshold. It also supports 140 languages for text tasks and 35 for multimodal understanding.
- Gemma 3n introduces novel components like KV Cache Sharing for faster streaming response generation, an upgraded audio encoder based on the Universal Speech Model (USM), and a new MobileNet-V5 vision encoder—pushing the boundaries of real-time, on-device multimodal AI.
- With over 160 million collective downloads across the Gemma ecosystem and models being used from enterprise CV pipelines to fine-tuned Japanese language variants, Gemma 3n is aimed at building scalable, offline, privacy-preserving AI.
Key Architectural Innovations
Per-Layer Embeddings (PLE)
-
Per-Layer Embeddings (PLE) is a technique designed to offload a significant portion of model memory requirements from high-speed device accelerators (like mobile GPUs or TPUs) to more accessible CPU memory, enabling large models to run on constrained devices without compromising performance.
-
PLE decouples the per-layer token embeddings from the core model, caching them separately and computing them efficiently outside of the accelerator. For example, while Gemma 3n models may have total parameter counts of 5B (E2B) and 8B (E4B), only about 2B and 4B of those parameters, respectively, are needed in active accelerator memory during inference. This leads to substantial reductions in required VRAM without a drop in model quality.
-
This optimization is particularly well-suited for edge deployment scenarios where accelerator memory is a bottleneck. The embedding computations can be executed on-device CPU threads and merged into the transformer’s residual pathways at runtime.
-
For instance, the elastic 2B submodel configuration (E2B) is a lightweight elastic submodel derived from a larger model (e.g., 4B or 8B), running with the efficiency of a 2B model by activating only a subset of the full architecture. The figure below (source) illustrates the Gemma 3n E2B model’s parameters running in standard execution versus an effectively lower parameter load using PLE caching and parameter skipping techniques. Put simply, with PLE, you can use Gemma 3n E2B while only having ~2B parameters loaded in your accelerator.

- From a deployment perspective, this mechanism empowers developers to run advanced Gemma 3n models on devices with as little as 2GB of RAM for E2B or 3GB for E4B—dramatically expanding the reach of high-quality on-device AI.
Matryoshka Transformer (MatFormer) Architecture
-
The Matryoshka Transformer (MatFormer) architecture, proposed in MatFormer: Nested Transformer for Elastic Inference by Devvrit et al. (2024), is central to Gemma 3n’s compute-efficiency. Inspired by Matryoshka dolls, it enables a larger model to contain smaller, independently usable submodels with no retraining or architecture changes required.
-
In Gemma 3n, MatFormer is the key to elastic inference: a single trained model (e.g., E4B) includes within it a lightweight, independently usable E2B model—and developers can also interpolate sizes between these via the Mix’n’Match method.
Nested FFN Block Design
-
The MatFormer architecture in Gemma 3n incorporates a nested structure within the Transformer block’s feedforward network (FFN), enabling dynamic submodel scaling during inference without incurring additional training costs.
-
MatFormer builds a hierarchy of Transformer blocks:
\[T_1 \subset T_2 \subset \cdots \subset T_g\]- where each block \(T_i\) shares parameters with its supersets, enabling parameter reuse and minimizing overhead. This design is centered in the FFN block, which is the primary contributor to a Transformer’s computational and memory demands—often accounting for over 60% of resource use in large language and vision models.
- Let:
- \(d_{\text{model}}\) be the model’s hidden dimension
- \(d_{\text{ff}}\) be the width of the FFN layer
- \(g\) be the number of granularities (typically 4)
- \(m_1 < m_2 < \cdots < m_g = d_{\text{ff}}\) be the neuron counts for each submodel
-
The FFN function for the \(i^{th}\) submodel is:
\[T^{\text{FFN}}_i(x) = \sigma(x \cdot W_1[0:m_i]^\top) \cdot W_2[0:m_i]\]- where:
- \[x \in \mathbb{R}^{d_{\text{model}}}\]
- \[W_1, W_2 \in \mathbb{R}^{d_{\text{ff}} \times d_{\text{model}}}\]
- \(\sigma\) is a nonlinearity, such as GELU or squared ReLU
- \(W[0:m_i]\) denotes selecting the top \(m_i\) rows from weight matrix \(W\)
- where:
- In practice, exponentially spaced FFN ratios are used:
-
This allows efficient sharing and ensures that the smallest submodel receives the most frequent gradient updates, enhancing training stability and representational consistency across granularities.
-
Each submodel \(M_i\) is built by stacking \(T_i\) across all layers:
\[M_i = [T_i]^\ell, \quad \text{for } i = 1, \ldots, g\]- with \(\ell\) being the total number of Transformer layers.
Training Strategy
- The training process for MatFormer follows a lightweight and elegant sampling-based strategy. At each training step, one of the \(g\) submodels is sampled randomly, and the corresponding parameters are updated via standard gradient descent.
-
Given a loss function \(L\), the training objective becomes:
\[L_{\text{sampling}}(x, y) = L(M_i(x), y)\]- where \(M_i\) is chosen uniformly at random from the nested submodels \(\{M_1, \ldots, M_g\}\). While uniform sampling is used in most settings, tuning the sampling distribution \(\{p_1, \ldots, p_g\}\) can yield performance gains—though even simple uniform distributions result in strong submodel accuracy.
-
This design ensures that:
- Shared parameters across models are updated frequently.
- Smaller submodels receive more updates due to their inclusion in every larger submodel.
- All submodels are jointly trained with no additional memory overhead.
- The result is a single, universal model \(M_g\) that embeds all submodels \(\{M_1, \ldots, M_{g-1}\}\) within itself—without the need for post-hoc pruning, distillation, or retraining.
Mix’n’Match Inference
-
Mix’n’Match Inference is a key feature enabled by the Matryoshka Transformer (MatFormer) architecture used in Gemma 3n. It allows developers to dynamically create hybrid submodels during inference by mixing granularities across different Transformer layers. While only a small number of submodels are explicitly optimized during training (typically 4, corresponding to different FFN widths), the nesting structure allows the formation of exponentially more configurations post-training.
- Submodel Construction:
- Instead of uniformly stacking one of the predefined granularities across all layers (e.g., using only \(T_2\) in every layer to build model \(M_2\)), Mix’n’Match selects different granularities for each layer. For example, layer 1 could use \(T_2\), layer 2 use \(T_3\), and so on.
- The following figure (source) illustrates the nested structure that MatFormer introduces into the Transformer’s FFN block & trains all the submodels, enabling free extraction of hundreds of accurate submodels for elastic inference.
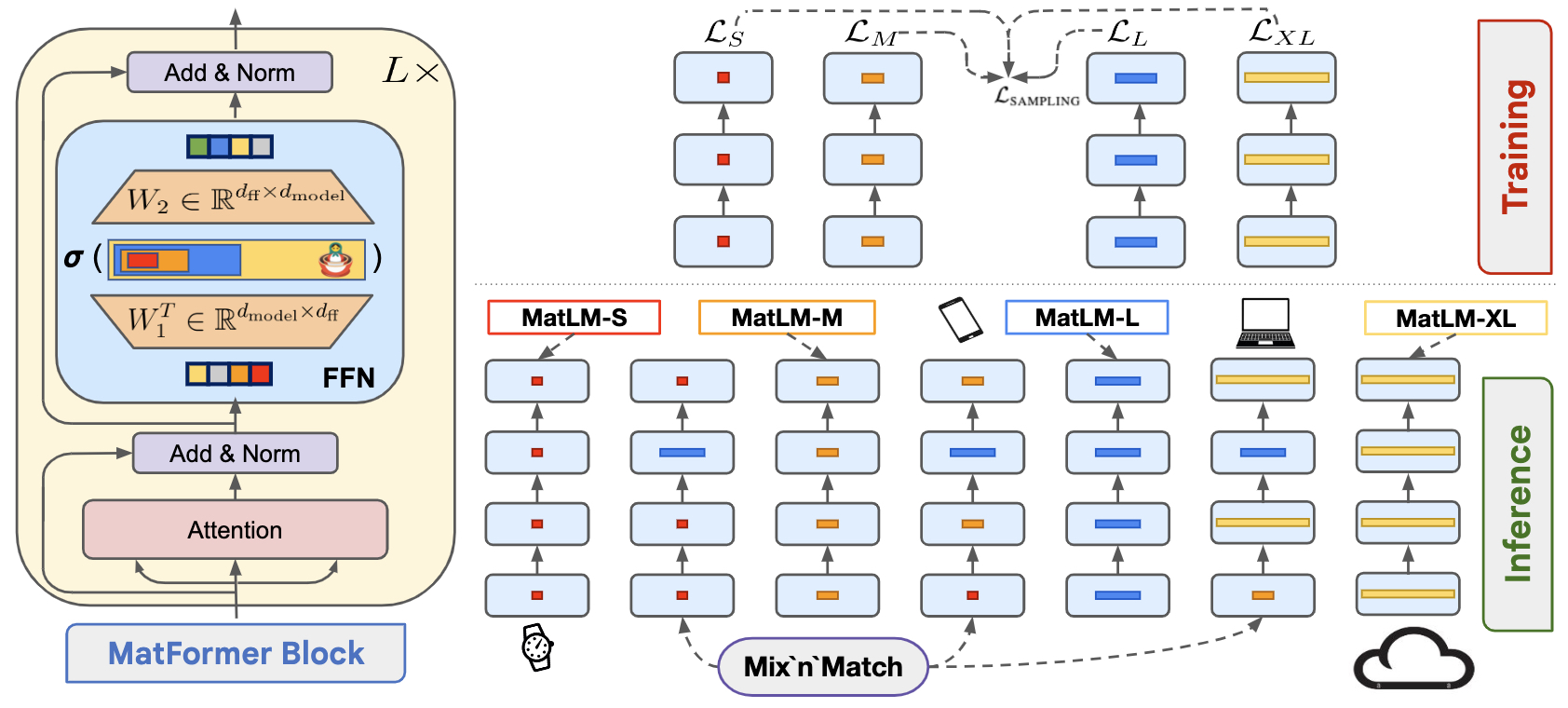
-
Exponential Flexibility: Given \(g\) granularities and \(\ell\) Transformer layers, the total number of possible submodels that can be formed via Mix’n’Match is \(g^\ell\). For instance, with 4 granularities and 24 layers, there are over 2.8 trillion possible configurations.
- Heuristic for Selection:
- A simple yet effective strategy for choosing which submodel to use is the monotonically non-decreasing granularity heuristic. That is, the model uses equal or increasing granularity levels as it progresses deeper into the network. Mathematically,
- This configuration aligns well with the training regime and tends to perform better than randomly mixed or non-monotonic configurations. Empirical results show that submodels formed this way maintain performance fidelity along the accuracy-compute tradeoff curve.
-
No Additional Training Required: These hybrid submodels are not trained individually. However, because the MatFormer architecture trains the shared parameters across all granularities, the Mix’n’Match models inherit the robustness and consistency of the trained submodels, showing strong performance even when their exact configuration was not seen during training.
-
Consistency and Deployment Benefits: The Mix’n’Match models maintain high output consistency with the full model (\(M_g\)), making them ideal for techniques like speculative decoding, where draft models propose outputs and a larger model verifies them. This consistency helps minimize rollbacks and speeds up inference.
- Efficiency and Adaptability: In resource-constrained settings, such as on-device inference, Mix’n’Match allows the model to adapt dynamically to available memory or compute budgets, selecting a configuration that maximizes performance for the given constraints.
Deployment Advantages
-
The blog post introduces MatFormer Lab, a tool that helps developers experiment with custom submodel configurations between E2B and E4B. These configurations are evaluated on benchmarks like MMLU to find optimal slices for specific use cases (MatFormer Lab).
-
Two main deployment modes emerge:
- Pre-extracted models: E2B is available as a separately exported model for fast deployment (up to 2x faster inference).
- On-the-fly slicing: Use Mix’n’Match to define custom models between E2B and E4B depending on current memory/compute availability.
-
Looking forward, the architecture is built to support runtime switching between submodels (e.g., transitioning from E4B to E2B mid-session), though this is not enabled in the current release.
-
MatFormer-based submodels are exported to TFLite
.taskcontainers and share parameter memory, enabling efficient co-location and dynamic dispatch during inference. -
These innovations support speculative decoding, adaptive workload tuning, and performance optimization on mobile chips—all without altering the architecture or retraining the model.
Integration in Gemma 3n
- MatFormer is the backbone of Gemma 3n’s nested model strategy. For example, the E2B model is a subset of E4B, achieved via FFN nesting.
- These submodels are exported to TFLite format and included in
.taskarchives, enabling scalable inference on-device with flexible tradeoffs between performance and resource use. - No architectural changes or re-training are needed when switching between sizes—Gemma simply activates a smaller slice of the model.
Conditional Parameter Loading
-
Conditional Parameter Loading is a runtime optimization strategy that allows Gemma 3n to load only the components relevant to a given task. For example, if the input is purely textual, the model can skip initializing its vision or audio encoders, thereby reducing memory overhead.
-
In Gemma 3n, this mechanism is particularly valuable because of the model’s native multimodality (text, image, audio, and video). By selectively activating only the necessary modules, such as the MobileNet-V5 vision encoder or the USM-based audio encoder, the system minimizes the active parameter set.
-
This approach works in tandem with Per-Layer Embeddings (PLE) and MatFormer, ensuring that both the core transformer layers and their auxiliary modules can operate within strict device memory constraints—often as low as 2GB for E2B models and 3GB for E4B.
-
Conditional Parameter Loading also simplifies deployment optimization:
- Developers can ship a single universal model and dynamically enable or disable modalities based on input signals.
- For static workloads, stripped-down models can be precompiled for even lower memory consumption.
-
When combined with features like KV Cache Sharing (for faster streaming prefill) and Mix’n’Match inference, this technique ensures that Gemma 3n achieves near cloud-level performance while staying resource-efficient on mobile hardware.
Model Components and Structure
-
Gemma 3n Architectural Innovations - Speculation and poking around in the model reverse-engineers Gemma 3n’s
.taskcontainer format and visual graph layout, confirming a modular design ideal for edge deployment, extensibility, and conditional loading. -
The developer blog also highlights that Gemma 3n is designed from the ground up for mobile-first, modular inference, using these
.taskZIP archives of TFLite models to pack specific functional components. This enables both fine-grained control during runtime and efficient updates of individual components (like vision encoders or tokenizers).
Core Modules and Functional Breakdown
-
Gemma 3n’s architecture comprises of the following modular components packed within
.taskZIP archives of TFLite models.-
TF_LITE_PREFILL_DECODE (2.55 GB):Main language model decoder component. -
TF_LITE_PER_LAYER_EMBEDDER (1.23 GB):Generates per-layer token-specific embeddings used in gating residual streams. -
TF_LITE_EMBEDDER (259 MB):Initial input embedding generator. -
TF_LITE_VISION_ENCODER (146 MB):Converts image input into dense feature embeddings. -
TF_LITE_VISION_ADAPTER (17 MB):Adapts visual embeddings into the language token stream. -
TOKENIZER_MODEL (4.5 MB):Subword tokenizer supporting a vocabulary of 262,144 tokens.
-
-
These components support a wide range of functionalities optimized for edge inference and are designed for extensibility via innovations like LAuReL and PLE.
Model Graph Exploration via Netron
-
Using tools like Netron, the unpacked TFLite models reveal the computation graph. Observations include:
- Modular layer sequencing aligned with MatFormer and PLE caching
- Runtime-skippable components (e.g., vision adapter paths via conditional parameter paths gated by input flags)
- Learned scalar parameters at merge points (consistent with LAuReL-RW)
- Substructure consistent with MatFormer’s nested FFN blocks
-
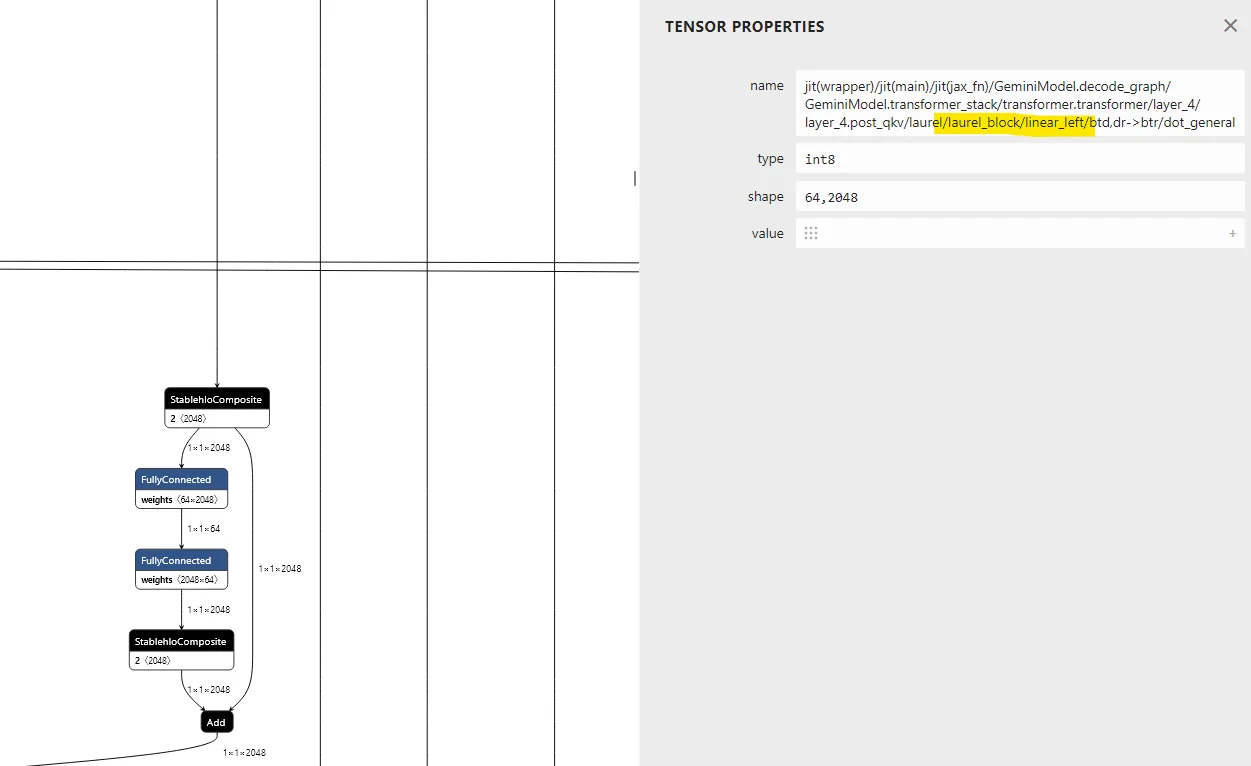
The following figure (source) illustrates the TFLite model computation graph as visualized in Netron from unpacked
.taskcontainers, showing Gemma 3n’s modular structure with components like the vision adapter routed via conditional parameter paths. This layout highlights composability, runtime-skippable submodules, and support for dynamic inference pathways—evidence of innovations like MatFormer and LAuReL-based gating.
Internal Transformer Structure and Residual Design
-
Gemma 3n uses 35 Transformer blocks, each with:
- Hidden dimension: 2048
- FFN expansion: up to 16,384 (with GeGLU activation)
- LAuReL-style modified residual pathways, modulated by PLE outputs
- Token-specific low-rank gates, dynamically computed per layer
-
These layers follow a layout similar to LAuReL-RW, with low-rank down-projection, token-aware gating, and re-projection before residual merging. This enhances fine-grained control over information flow per token and per layer.
-
The following figure (source) shows the flow of Gemma 3n’s transformer blocks illustrating token-conditioned low-rank projections modulating the residual stream. This confirms the presence of modified residual connections resembling LAuReL-RW, with 35 blocks, a 2048-dimensional core, and GeGLU-activated 16384-wide FFNs—supporting both depth and dynamic token-specific gating. The structure reveals layer-wise low-rank projections gated by PLE outputs, consistent with LAuReL principles.
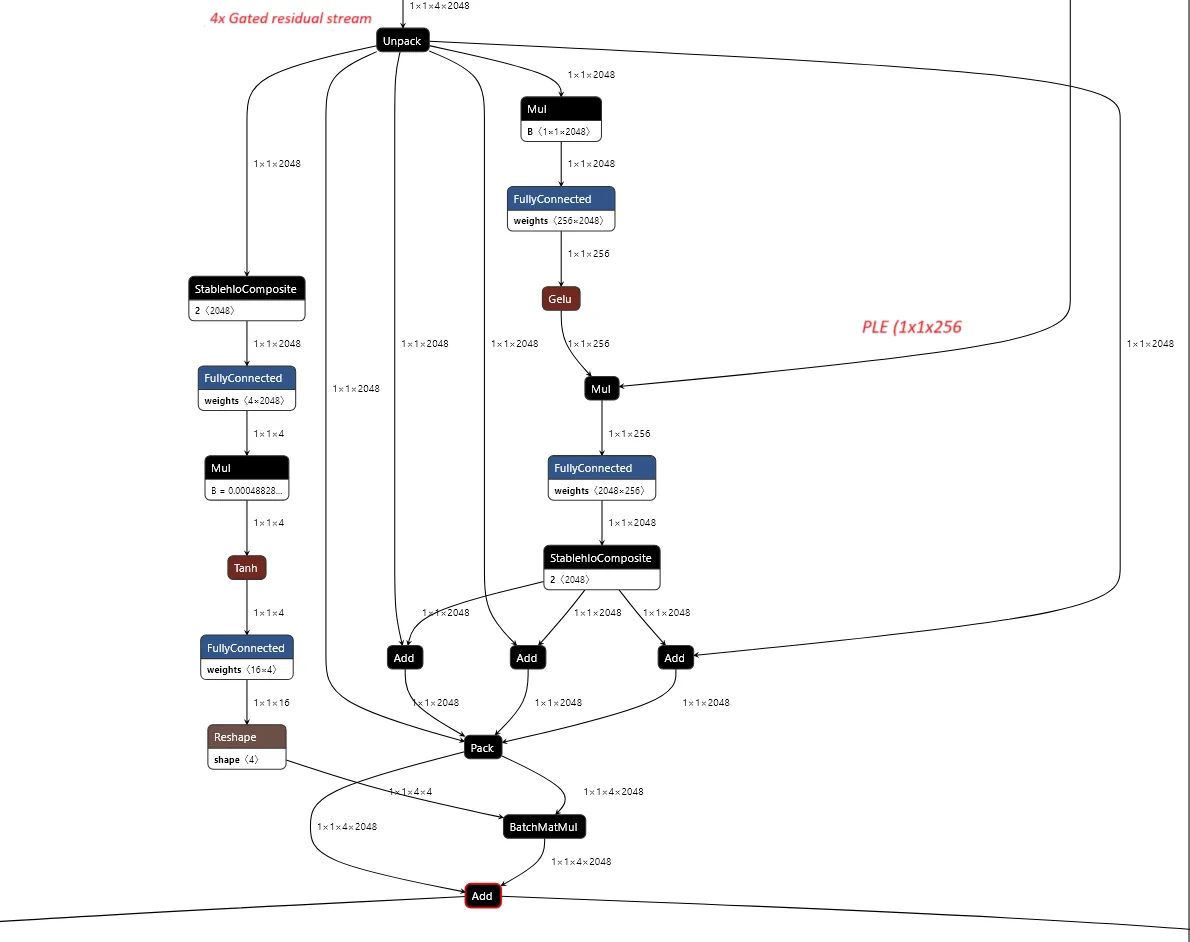
Learned Augmented Residual Layer (LAuReL)
-
Proposed in LAuReL: Learned Augmented Residual Layer by Menghani et al. (2025), LAuReL generalizes standard residual connections:
\[x_{i+1} = \alpha \cdot f(x_i) + g(x_i, x_{i-1}, \ldots, x_0)\]- where \(\alpha\) is a learnable scalar and \(g(\cdot)\) is a learned linear map (e.g., low-rank transformation or weighted combination of past activations).
-
Inferred Implementation in Gemma 3n:
- Applies low-rank down-projection to residual streams
- Multiplies the projection by a token-specific gate from the PLE module
- Re-projects to full dimension and merges with non-linear output
- Uses forms similar to LAuReL-RW and LAuReL-LR variants
-
The following figure (source) shows a detailed Netron view of LAuReL-style residual merging. Shows residual down-projection, modulation by token-specific gate, and re-projection to full dimension before merging—indicating implementation of LAuReL-RW with PLE-driven control.
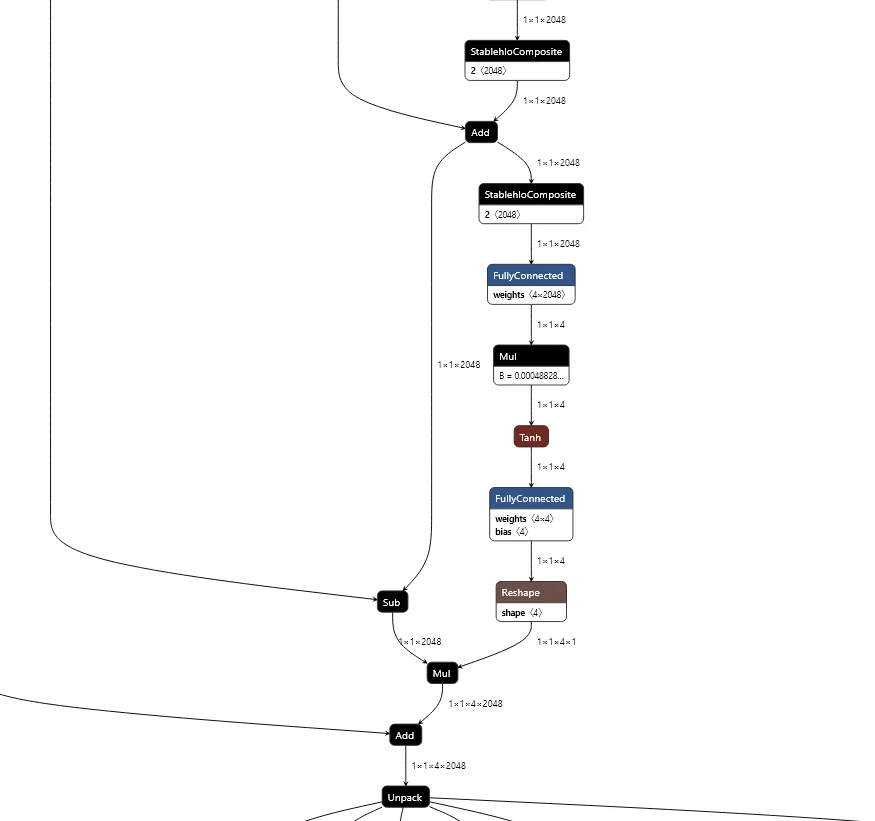
Per-Layer Embedding Mechanism
-
The
TF_LITE_PER_LAYER_EMBEDDERholds large token-layer lookup tables of shape \(262144 \times 256 \times 35\), producing 256-dimensional embeddings per token per layer. These embeddings modulate a down-projected residual stream:- Residual stream (2048) → downprojected to 256
- Element-wise multiplied with per-token embedding
- Re-projected to 2048 and added back
-
This is conceptually similar to a token- and layer-conditioned LoRA gating mechanism.
-
The following figure (source) illustrates how per-layer embeddings gate residual information. It shows the <>-token lookup interaction and confirms the use of layer-specific control mechanisms in Gemma 3n.
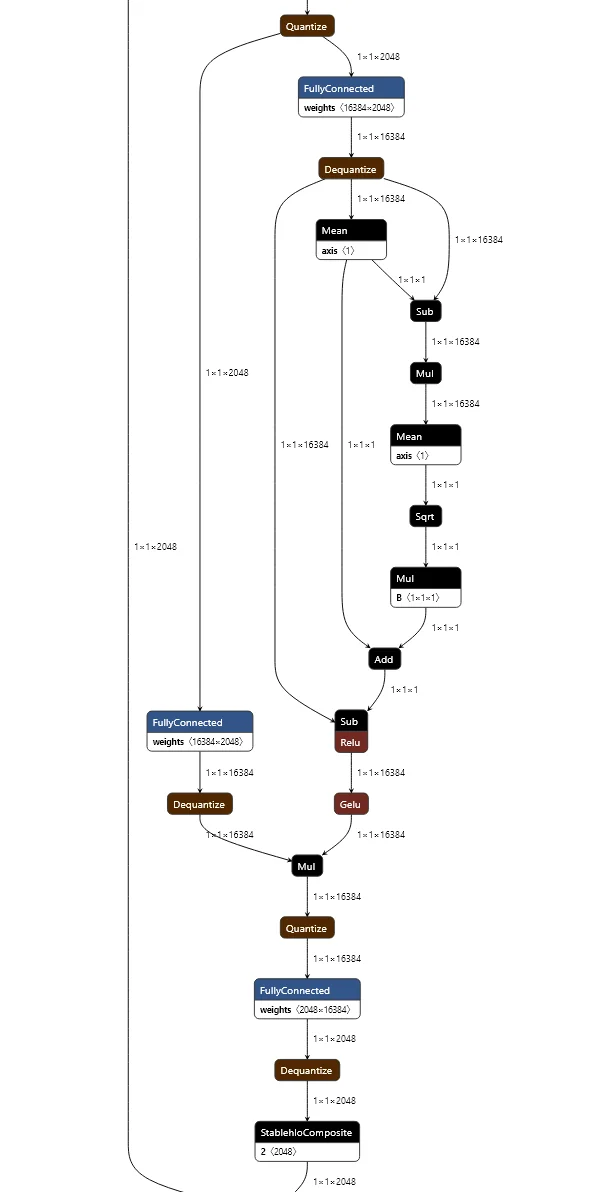
Alternating Updates for Efficient Transformers (AltUp)
-
Alternating Updates (AltUp), proposed in Alternating Updates for Efficient Transformers by Baykal et al. (2023), is a technique designed to increase a transformer’s representational capacity (e.g., wider token embeddings) without incurring a proportional increase in computation or memory overhead. It is particularly relevant to on-device architectures like Gemma 3n, where hardware constraints demand high efficiency at runtime.
-
AltUp widens the representation dimension (e.g., from 2048 to 4096) but avoids computing over the entire width in each layer. Instead, each transformer layer updates only a sub-block (e.g., one-quarter) of the full vector, and uses a lightweight predict-correct mechanism to infer updates for the rest.
Core Idea: Predict–Compute–Correct
-
Suppose the token representation is expanded from dimension \(d\) to \(K \cdot d\). AltUp divides this expanded vector into \(K\) chunks, e.g., for \(K = 2\):
\[x = \text{concat}(x_1, x_2)\] -
At each transformer layer:
- Predict: Compute an estimate \(\hat{x}_i\) for each sub-block as a linear combination of the others.
- Compute: Apply the transformer layer to only one sub-block (e.g., \(x_1\)).
- Correct: Use the updated sub-block to refine predictions for all other sub-blocks.
-
This approach ensures that each part of the expanded representation gets updated across layers (e.g., via round-robin or alternating scheduling) without processing the full width at once.
Efficiency Benefits
-
AltUp avoids the quadratic scaling of computation cost with dimension width. Instead of \(O(K^2d^2)\) for a naïvely widened model, AltUp achieves \(O(d^2 + K^2d)\) complexity per layer.
-
Only a few learnable parameters are introduced per layer (on the order of \(K^2 + K\)), and memory impact is minimal. At inference, the Key-Value cache is unaffected, which is essential for real-time generation tasks.
-
The method scales well and shows up to 87% speedups on benchmarks like SuperGLUE and SQuAD when applied to T5 models, without loss in accuracy.
Practical Extensions
-
Recycled-AltUp: Avoids expanding the embedding table by reusing a narrow embedding and duplicating it across chunks. At the output layer, it sums the sub-blocks and projects back to standard size. This offers improved speed and parameter efficiency with negligible loss in quality.
-
Sequence-AltUp: Applies the AltUp strategy to the sequence dimension instead of the embedding dimension. It selectively processes only a subset of sequence positions in each layer (similar to strided sampling) while predicting and correcting the rest. This drastically reduces attention computation in long contexts.
Integration with Gemma 3n
-
While not explicitly documented in the public Gemma 3n architecture, the developer blog confirms that AltUp is one of the novel architectural components behind its mobile-first design. In conjunction with LAuReL and MatFormer, it helps Gemma 3n achieve competitive performance under strict compute and memory limits.
-
AltUp’s low implementation complexity and synergy with other techniques like MoE or MatFormer make it a strong candidate for future multimodal model stacks that demand elastic scaling and efficient representation learning.
Performance and Deployment
- Gemma 3n is built to offer frontier-model performance on edge hardware, supporting text, image, audio, and video modalities. With its flexible submodeling (E2B and E4B), adaptive computation strategies (MatFormer, PLE, AltUp), and runtime-efficient designs (KV cache sharing, conditional parameter loading), it is capable of powering high-quality experiences with minimal device resources.
-
The model is accessible for experimentation and deployment through platforms such as Google AI Studio and Hugging Face, providing developers with the tools to integrate Gemma 3n into various applications.
-
The E2B model performs efficiently with approximately 2GB of RAM, and the E4B model with about 3GB, even though their total parameter counts are 5B and 8B respectively. This is made possible by:
- PLE caching which offloads large token-layer embeddings to CPU memory
- Conditional parameter loading that disables unused modules
- Alternating Updates and MatFormer for memory-bounded forward passes
-
Multilingual and multimodal capabilities:
- Gemma 3n supports 140 languages for text tasks and 35 languages for image/video/multimodal understanding.
- The audio encoder (based on Universal Speech Model) supports high-accuracy ASR and speech translation — with particularly strong AST results in English ↔ Spanish, French, Italian, Portuguese.
- Multimodal understanding is backed by the MobileNet-V5-300M vision encoder, delivering 13x faster performance on Google Pixel Edge TPUs compared to Gemma 3’s SoViT baseline.
-
Benchmark Results:
- On LMArena, E4B is the first sub-10B model to exceed 1300 points.
- Mix’n’Match variants tuned using MatFormer Lab achieve optimal compute-accuracy tradeoffs for different deployment targets (e.g., low-latency generation vs. high-fidelity reasoning).
-
Inference Optimization Features:
- KV Cache Sharing enables 2x faster prefill stages by directly sharing intermediate attention keys/values across layers.
- Speculative decoding benefits from high consistency between Mix’n’Match submodels and the full model, reducing rollbacks.
- Vision encoder supports up to 60 FPS real-time inference with multiple input resolutions (256×256 to 768×768).
- Audio encoder processes up to 30 seconds of input with support for streaming, making it viable for real-time ASR/AST applications.
-
Deployment Ecosystem:
- Available on platforms including Google AI Studio, Hugging Face, and Kaggle.
- Supported toolchains include:
llama.cpp, MLX, Ollama, SGLang, vLLM, NVIDIA API Catalog, TRL, Docker, and LMStudio. -
Developers can deploy via:
- Google GenAI API
- Vertex AI
- Edge TPUs via Google AI Edge Gallery
- Gemma 3n is part of the broader Gemmaverse—a growing family of specialized models with over 160 million downloads. Its design reflects a deep focus on sustainability, democratization of access, and the growing demand for offline-capable, privacy-preserving AI.
References
- Introducing Gemma 3n: The developer guide
- What is Gemma 3n and How to Access it? - Analytics Vidhya
- Gemma 3n model overview
- Gemma 3n Architectural Innovations - Speculation and poking around in the model
Citation
@article{Chadha2020Gemma3n,
title = {Gemma 3n},
author = {Chadha, Aman and Jain, Vinija},
journal = {Distilled AI},
year = {2020},
note = {\url{https://aman.ai}}
}