Federated Learning (FL)

Overview

  • Federated Learning (FL) is a machine learning paradigm designed for scenarios where data is distributed across multiple devices or organizations, and privacy or logistical concerns make it undesirable or illegal to centralize that data. FL enables collaborative model training while keeping all raw data local to each client, thus mitigating privacy risks and reducing communication overhead compared to transferring large datasets.

  • Originally introduced to enable on-device learning (e.g., mobile keyboards, IoT devices), FL is now central to many privacy-preserving and distributed AI strategies, particularly in healthcare, finance, and mobile personalization.

Motivations

  • Data privacy regulations (GDPR, HIPAA) restrict centralized storage of user data.
  • Bandwidth constraints and data sovereignty make uploading large volumes of data impractical or noncompliant.
  • In many real-world cases, data is non-i.i.d. (not identically distributed across clients) and can be heavily skewed, e.g., language dialects across users or hospitals with different patient demographics.

Privacy-Preserving AI via FL

  • FL plays a foundational role in building privacy-preserving AI systems by ensuring:

    • Raw user data never leaves its source. This drastically reduces the risk of data leakage from centralized storage or transit pipelines.
    • Client updates (e.g., gradients or model weights) can be encrypted and anonymized, further mitigating the risk of inference attacks.
    • FL can be combined with other privacy-preserving techniques such as Differential Privacy (DP) and Secure Aggregation, forming a robust stack that provides both empirical and theoretical privacy guarantees.
    • Enables learning from sensitive data such as electronic health records, legal case documents, or personal conversations without exposing them, allowing AI systems to leverage such data responsibly.

  • This architecture is especially critical for deploying responsible AI in regulated or user-facing environments—ensuring compliance, maintaining user trust, and reducing ethical and legal liabilities.

Definition

  • At its core, FL aims to train a global model collaboratively over a network of K clients, each with access to its own private dataset. Instead of aggregating raw data centrally, each client performs local training and contributes to a shared global model via periodic updates.

  • Let the overall learning objective be:

    \[\min_{w} f(w) = \sum_{k=1}^{K} \frac{n_k}{n} F_k(w)\]

    • where:

      • \(w \in \mathbb{R}^d\): global model parameters,
      • \(F_k(w)\): the local empirical risk (loss function) on client \(k\),
      • \(n_k\): the number of data points on client \(k\),
      • \(n = \sum_{k=1}^{K} n_k\): total number of training samples across all clients.

  • Each client updates its local version of the model \(w_k^{(t)}\) using its private dataset \(\mathcal{D}_k\), computes the local update (via SGD or other optimizers), and sends either:

    • Model weights \(w_k^{(t+1)}\), or

    • Weight deltas \(\Delta w_k = w_k^{(t+1)} - w^{(t)}\)

    • … back to a central server.

  • The server then aggregates all received updates using a weighted average:

\[w^{(t+1)} = \sum_{k=1}^{K} \frac{n_k}{n} w_k^{(t+1)}\]
  • This process, known as Federated Averaging (FedAvg), repeats for multiple rounds until convergence.

Key Concepts:

  • Local Training: Each client performs one or more gradient descent steps on its local dataset.
  • Periodic Aggregation: Updates are sent to the server only periodically to reduce communication overhead.
  • Weighted Contributions: Clients with more data contribute proportionally more to the global model.

Comparison to Centralized and Distributed Learning:

  • Unlike traditional centralized learning, FL does not transfer any raw data to the server.

  • Unlike classical distributed training, FL assumes that client data may be non-i.i.d., unbalanced, and held by unreliable or resource-constrained devices (e.g., smartphones, hospitals).

  • This definition forms the mathematical backbone of the FL paradigm. In practice, several enhancements—like asynchronous communication, secure aggregation, and personalization—are layered on top to make FL robust and scalable in real-world systems.

Types of Federated Learning

  • FL can be applied in various architectural and organizational setups depending on the scale, reliability, and connectivity of the participants. These use cases fall into two main categories:

Cross-Device Federated Learning

  • Involves a massive number of edge devices—e.g., smartphones, wearables, or IoT sensors—that intermittently participate in training.

  • Typical characteristics:

    • Millions of clients.
    • Sparse participation (often <10% active per round).
    • Highly diverse hardware, data distributions, and power/network availability.
  • Ideal for on-device personalization, mobile input prediction, and private assistant models (e.g., Google’s Gboard).

Cross-Silo Federated Learning

  • Involves a smaller number (typically 2–100) of reliable institutions or data silos such as hospitals, banks, or data centers.

  • Typical characteristics:

    • High bandwidth and computational capacity.
    • Stable, long-lived training participation.
    • Institutional data often exhibits statistical heterogeneity.
  • Use cases include medical AI across hospitals or fraud detection across banks.

Centralized Federated Learning

  • In this classic setup, a central server orchestrates the learning process by:

    • Selecting clients for each round.
    • Sending the current global model \(w^{(t)}\) to selected clients.
    • Aggregating updates to form a new model \(w^{(t+1)}\).

  • This is the most commonly implemented setup and serves as the foundation for algorithms like FedAvg and FedProx.

  • FL Round Mechanics:

    To ensure good task performance of the global model, FL is conducted in rounds. Each round consists of several key stages:

    • Initialization: The server initializes the global model parameters. A machine learning model such as a neural network, linear regressor, or boosted tree is selected and broadcast to participating clients.

    • Client Selection: A random fraction of clients is selected. Only selected clients participate in training during the current round.

    • Configuration: The server configures local training instructions, such as the number of mini-batch gradient steps or local epochs.

    • Local Training: Each selected client performs local training on its private data using the received model.

    • Reporting: Clients send either full model weights or weight deltas back to the server. The server aggregates the updates using a weighted average and updates the global model.

    • Termination: The training process repeats for multiple rounds. It is terminated based on convergence criteria such as number of rounds or global model accuracy.

  • This process assumes synchronized rounds, where updates are collected after all clients complete training. However, asynchronous variants allow updates to be returned as soon as layer-wise computations are done (a technique known as split learning), which reduces latency and allows training with clients of varying capabilities.

  • Diagram:

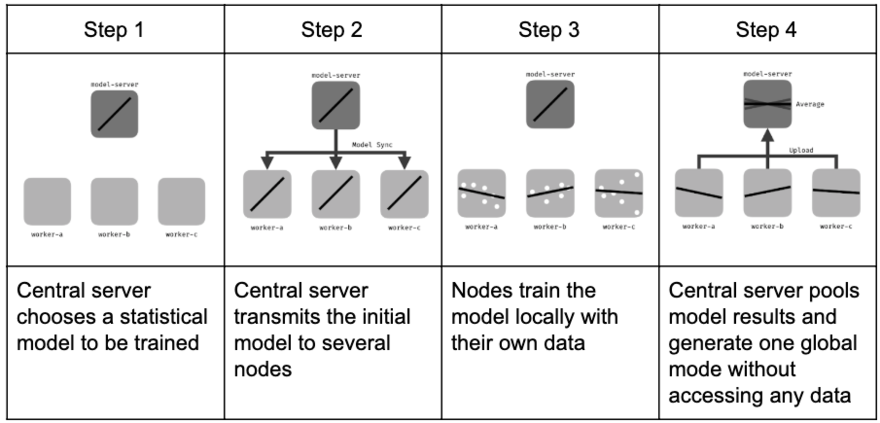
  • Implementation Note: In asynchronous setups, layer-wise updates may be sent incrementally to the server, and model fusion must consider partial updates. Failure handling and node dropout recovery are also necessary in practical deployments.

  • Beyond the centralized model, peer-to-peer decentralized variants can replace the central server using gossip-based or consensus mechanisms to enable collaborative training without a single orchestrator. These models require additional design for communication protocols, node synchronization, and consistency guarantees.

Decentralized Federated Learning

  • The way statistical local outputs are pooled and the way nodes communicate can vary significantly from the centralized setup. In particular, orchestrator-less distributed networks are a key variation, leading to the concept of decentralized FL.

  • In these decentralized networks:

    • There is no central server to coordinate training or aggregate models.
    • Each node communicates with a subset of peers, often chosen randomly.
    • Nodes send local updates to neighbors, who aggregate the models locally.

  • This peer-to-peer model aggregation reduces the number of transactions and can lower overall communication and compute cost. It also removes the single point of failure and may improve fault tolerance and privacy.

  • However, decentralized setups introduce new challenges such as:

    • Synchronization across distributed nodes.
    • Robustness of the aggregation protocol.
    • Efficiency of gossip-based or consensus-based communication schemes.

Heterogeneous Federated Learning

  • In real-world deployments, clients are rarely uniform. Devices may differ in:

    • CPU/GPU capabilities,
    • battery life and memory,
    • connectivity bandwidth, and
    • local dataset sizes and distributions.

  • To address these constraints, frameworks like HeteroFL allow for:

    • Varying model capacities across clients.
    • Asynchronous updates.
    • Layer-wise freezing or sharing to reduce load on low-power devices.

  • Non-IID Data Challenges:

    In FL, client data is often non-iid. The performance of the global model is affected by:

    • Covariate shift: Clients hold features from different distributions.
    • Prior probability shift: Label distributions differ across clients.
    • Concept drift: Same labels, different feature distributions.
    • Concept shift: Same features, different labeling.
    • Unbalanced data: Different clients may have vastly different data volumes.

  • Addressing non-iid data may involve sophisticated normalization strategies (beyond batch normalization) or adopting algorithms like FedDyn that are robust to data heterogeneity.

Implementation Details

  • Beyond system-level optimizations and privacy techniques, FL implementations often involve tuning key training hyperparameters:

    • Number of FL rounds (\(T\))
    • Total number of nodes (\(K\))
    • Fraction of nodes per round (\(C\))
    • Local batch size (\(B\))
    • Number of local updates before aggregation (\(N\))
    • Local learning rate (\(\eta\))

  • These parameters are adjusted based on deployment constraints such as compute capacity, memory, bandwidth, and convergence speed. For instance, using a smaller fraction \(C\) of participating nodes per round reduces overhead and improves training scalability while mimicking the benefits of stochastic gradient descent.

  • Additionally, orchestrator-less topologies enable clients to send model updates directly to a subset of peers, reducing communication bottlenecks and increasing fault tolerance. Put simply, in this case, there is no central server dispatching queries to local nodes and aggregating local models. Each local node sends its outputs to several randomly-selected others, which aggregate their results locally. This constrains the number of transactions, thereby sometimes reducing training time and computing cost.

Federation Algorithms

  • Various algorithmic strategies have been proposed to optimize training dynamics and convergence in FL, especially in the presence of non-iid data or system heterogeneity.

Federated Stochastic Gradient Descent (FedSGD)

  • FedSGD is the most basic form of federated optimization, adapting traditional stochastic gradient descent to a distributed, privacy-sensitive environment. It was first formalized in McMahan et al.’s seminal work on federated learning, Communication-Efficient Learning of Deep Networks from Decentralized Data (McMahan et al., 2017).

  • In FedSGD, at each communication round, a random subset of clients is selected. Each participating client computes the gradient of the current global model on its full local dataset and transmits this gradient to the central server. Unlike centralized SGD where the gradient is computed over a mini-batch, FedSGD effectively computes local gradients on the entire dataset of each selected client:

    \[g_k^{(t)} = \nabla F_k(w^{(t)}) = \frac{1}{n_k} \sum_{i=1}^{n_k} \nabla \ell(w^{(t)}; x_{i,k})\]

  • The server then performs a weighted aggregation of the gradients, proportional to the number of local samples \(n_k\), to form the global gradient:

    \[g^{(t)} = \sum_{k \in S_t} \frac{n_k}{n_{S_t}} g_k^{(t)}\]
    • where \(S_t\) is the subset of clients participating at round \(t\), and \(n_{S_t} = \sum_{k \in S_t} n_k\).

The gradients are thus averaged by the server proportionally to the number of training samples on each node, and used to make a gradient descent step.

  • The global model is then updated via:

    \[w^{(t+1)} = w^{(t)} - \eta \cdot g^{(t)}\]
    • where \(\eta\) is the learning rate.

  • This approach is simple and communication-efficient when clients are assumed to have high computational power and small local datasets. However, it performs only one local update per round and hence can converge slowly in practice, especially when client participation is sparse or datasets are large.

  • The original FedSGD strategy serves as a theoretical foundation and limiting case of the more practical FedAvg algorithm, which allows multiple local SGD steps per round to improve convergence without increasing communication frequency.

FedAvg (Federated Averaging)

  • This foundational method introduced the concept of federated averaging for decentralized model training, published in Communication‑Efficient Learning of Deep Networks from Decentralized Data by McMahan et al., 2017.

  • FedAvg combines local stochastic gradient descent (SGD) on each client with periodic model averaging on a central server. The key insight is that communication efficiency can be vastly improved by allowing multiple local updates before averaging.

  • Server Process:

    • Initialize global model weights \(w^{(0)}\)

    • For each round \(t\):

      • Sample a subset \(S_t \subseteq \{1, \dots, K\}\) of participating clients.
      • Send current model \(w^{(t)}\) to all selected clients.
      • Receive updated models \(w_k^{(t+1)}\) after local training.
      • Aggregate updates as:
      \[w^{(t+1)} = \sum_{k \in S_t} \frac{n_k}{n_{S_t}} w_k^{(t+1)}\]
      • where \(n_{S_t} = \sum_{k \in S_t} n_k\)

  • Client Process:

    • Receive global weights \(w^{(t)}\).
    • Train locally using SGD for \(E\) epochs over local dataset \(\mathcal{D}_k\).
    • Return updated weights \(w_k^{(t+1)}\) to server.

  • FedAvg generalizes FedSGD by allowing local multiple gradient descent steps per round. This makes it more robust and scalable, especially under communication constraints.

  • Theoretical Insights from McMahan et al. (2017):

    • FedAvg performs well even when client data is non-IID and unbalanced, although convergence can slow in such settings.
    • Larger local epochs \(E\) can reduce communication rounds, but might increase model drift.
    • The paper demonstrates practical convergence across MNIST, CIFAR-10, and language modeling tasks using LSTM models on mobile keyboards.

  • Advantages:

    • Simplicity: Easy to implement and tune.
    • Efficiency: Reduces communication rounds.
    • Scalability: Tested on large-scale FL setups like Gboard.

FedProx

  • FedProx, introduced in Federated Optimization in Heterogeneous Networks by Li et al. (2018), is a generalization of FedAvg that incorporates a proximal term into the local optimization objective. This addition explicitly addresses the statistical heterogeneity and system variability often observed in FL settings.

  • Local Objective:

    \[\min_w \, F_k(w) + \frac{\mu}{2} \| w - w^{(t)} \|^2\]
    • Here, \(F_k(w)\) is the local objective on client \(k\), \(w^{(t)}\) is the global model at round \(t\), and \(\mu\) is the proximal coefficient that controls how much local updates deviate from the global state.

  • Key Properties:

    • The proximal term limits the distance between local model parameters and the global model during each round.
    • This helps stabilize updates from clients with highly non-i.i.d. data or inconsistent computational capabilities.

  • Theoretical Contributions:

    • The paper proves convergence rates under mild assumptions, including cases with variable local solvers (e.g. incomplete local convergence).
    • It introduces a partial participation framework that captures realistic settings where only a fraction of clients participate per round.

  • Benefits:

    • Improved convergence in heterogeneous environments where FedAvg fails or is unstable.
    • Allows flexible local computation, enabling straggler mitigation without penalizing global model performance.

  • Implementation Tips:

    • The proximal coefficient \(\mu\) should be tuned based on the level of heterogeneity—higher values work better when local data distributions are more divergent.
    • Compatible with many local solvers and can be integrated with mini-batch SGD or adaptive optimizers.

SCAFFOLD

  • Introduced in Stochastic Controlled Averaging for Federated Learning by Karimireddy et al. (2020), Stochastic Controlled Averaging for Federated Learning (SCAFFOLD) addresses the slow and unstable convergence often observed in federated settings with non-i.i.d. data distributions. SCAFFOLD applies control variates to mitigate the effects of client drift by correcting the updates made by individual clients during training.

  • Core Idea: In non-i.i.d. settings, local updates may diverge from the global objective due to statistical heterogeneity. SCAFFOLD introduces a variance reduction mechanism using control variates to keep local training aligned with the global direction of optimization.

  • Mechanism:

    • Each client maintains a local control variate \(c_k\), while the server holds a global control variate \(c\). These variates estimate the direction and scale of updates.

    • During local training on client \(k\), the update is modified as follows:

      \[w_k^{(t+1)} \leftarrow w_k^{(t)} - \eta \left( \nabla F_k(w_k^{(t)}) - c_k + c \right)\]

      where:

      • \(\eta\) is the learning rate,
      • \(\nabla F_k(w_k^{(t)})\) is the gradient of the local loss,
      • \(c_k\) is the local control variate,
      • \(c\) is the global control variate.

    • After local training, both the local model \(w_k\) and the updated control variate \(c_k\) are sent back to the server.

    • The server aggregates the received models and updates the global control variate accordingly.

  • Theoretical Guarantees:

    • The authors show that SCAFFOLD can achieve linear speedup (with respect to the number of clients) under certain assumptions.

    • It provides a provable reduction in client drift and performs better than FedAvg especially in the non-i.i.d. regime.

    • Unlike other methods that require full client participation or proximal terms, SCAFFOLD is robust to partial participation and reduces the number of communication rounds required to achieve a target accuracy.

  • Benefits:

    • Significantly faster convergence under client heterogeneity.
    • Theoretically grounded variance reduction using control variates.
    • More efficient in both communication and compute under typical federated conditions.

MIME

  • Introduced in Mime: Mimicking Centralized Stochastic Algorithms in Federated Learning by Karimireddy et al. (2021), Mimicking Centralized Stochastic Algorithms (MIME) bridges the gap between centralized and federated training by incorporating global optimizer states like momentum and variance tracking.

  • Key Idea:

    • Clients mimic centralized SGD behavior by combining local updates with a server-side optimizer (e.g., momentum SGD or Adam).
    • MIME introduces control variates at the server level, capturing gradient differences that correct for stale or drifting local updates.
    • Server sends both the model parameters and a preconditioned gradient to each client. Clients perform local SGD using this guidance to align with centralized dynamics.

  • Mechanism:

    • The global server maintains a momentum buffer or preconditioner (e.g., gradient moving average).

    • Each client performs the following at round \(t\):

      \[w_k^{(t+1)} = w^{(t)} - \eta \left( \nabla F_k(w^{(t)}) - \nabla F_k(w^{(t-1)}) + \bar{g}^{(t)} \right)\]

      • where:

        • \(\bar{g}^{(t)}\) is the server-side momentum gradient,
        • \(\nabla F_k(w^{(t)})\) and \(\nabla F_k(w^{(t-1)})\) are local gradients at current and previous iterations.

  • Benefits:

    • Effectively reduces client drift in heterogeneous data settings.
    • Improves convergence speed and final model accuracy across various FL benchmarks (e.g., EMNIST, CIFAR-10).
    • Compatible with advanced optimizers like Adam and RMSprop due to its modular design.
    • Empirically shown to outperform FedAvg and FedProx in both IID and non-IID scenarios with fewer communication rounds.

  • Implementation Notes:

    • MIME can be implemented by augmenting a FedAvg setup with an extra gradient tracking module at the server.
    • Clients must retain a copy of their previous model state to compute gradient deltas.
    • Performance benefits are highest in regimes with high heterogeneity and sparse client participation.

FedDyn

  • Presented in Federated Learning Based on Dynamic Regularization by Acar et al. (2021), Federated Learning with Dynamic Regularization (FedDyn) addresses the core challenge of objective inconsistency between local client losses and the global optimization objective under data heterogeneity. In typical federated learning scenarios, the optimization problem aims to minimize the global loss across all clients:

    \[\min_{w} \left\{ f(w) = \sum_{k=1}^K \frac{n_k}{n} F_k(w) \right\}\]
    • where \(F_k(w)\) is the empirical loss on client \(k\). However, in non-i.i.d. settings, minimizing \(F_k(w)\) individually on each client may not lead to convergence of \(f(w)\).

  • FedDyn introduces a dynamically updated regularization term in each client’s local objective to mitigate this discrepancy. Specifically, FedDyn modifies the local objective function as follows:

    \[\tilde{F}_k(w) = F_k(w) - \langle \nabla f(w_t), w \rangle + \frac{\lambda}{2} \| w - w_t \|^2\]

    • where:

      • \(w_t\) is the global model at round \(t\),
      • \(\nabla f(w_t)\) is an approximation of the global gradient at \(w_t\),
      • \(\lambda\) is a regularization coefficient.

  • This regularization acts as a bias-correction mechanism, aligning local descent directions with the global objective. By integrating both the history of updates and a proximal term, FedDyn ensures that each client’s optimization path stays consistent with the global descent trajectory.

  • Advantages:

    • Demonstrates convergence guarantees for non-convex losses under arbitrary heterogeneity assumptions.
    • Empirically outperforms other baselines such as FedAvg and FedProx on diverse datasets (e.g., CIFAR-10, FEMNIST, Shakespeare), especially under high data non-i.i.d.-ness.
    • The method reduces client drift and improves both convergence speed and final accuracy.

  • FedDynOneGD:

    • A lightweight extension that performs only one gradient computation per client per round.
    • Reduces local computation from multiple SGD steps to a single pass, with linear complexity in the number of local examples.
    • Suitable for low-power or resource-constrained devices while retaining the convergence behavior of the full FedDyn formulation.

  • These innovations position FedDyn as a communication-efficient, robust, and heterogeneity-aware alternative for real-world federated learning deployments, where computational and statistical variance across clients is significant.

Comparative Analysis of Algorithmic Variants

Algorithm Paper (Year) Core Innovation Heterogeneity Robustness
FedSGD McMahan et al. 2017 (arXiv) Global gradient updates from full local datasets Low
FedAvg McMahan et al. 2017 (flower.ai, Wikipedia, arXiv) Simple weighted averaging of local models Moderate
FedProx Li et al. 2018 (arXiv, proceedings.mlsys.org) Local proximal updates to limit drift Improved stability
SCAFFOLD Karimireddy et al. 2020 (arXiv, cs.nyu.edu) Control variate correction per client Very robust
MIME Karimireddy et al. ICLR 2021 (arXiv, OpenReview) Mimic centralized optimizers with local drift correction Strong
FedDyn Acar et al. ICLR 2021 (arXiv, OpenReview) Dynamic loss regularization per-device High robustness

Implementation Details

  • FL systems involve a complex interplay between system-level constraints (communication, compute, network availability) and algorithmic robustness (privacy, convergence, fairness). Below are practical implementation techniques that ensure real-world deployment feasibility—especially for large-scale federated setups like those involving LLM fine-tuning.

Communication Optimizations

  • Compression & Sparsification: Transmit only top‑k updates (e.g., 1%–10% of gradients), apply quantization (e.g., 8‑bit or ternary encoding), or use sketching techniques like Count Sketch to reduce message size.

  • Asynchronous Updates: In setups with highly variable client response times, asynchronous FL enables continuous server-side aggregation without stalling. This requires additional mechanisms to ensure consistency (e.g., staleness-aware updates).

  • Dropout Resilience: Ensure robustness to client churn by training with randomly dropping clients each round. This also regularizes the model and avoids overfitting to certain users.

Privacy & Security

  • Differential Privacy (DP-FL): Combine local gradient clipping with Gaussian noise (via DP-SGD) to bound each client’s contribution to the global model. This yields per‑round guarantees of \((\varepsilon, \delta)\)-DP, with accounting accumulated over rounds.

  • Secure Aggregation: Use cryptographic techniques (e.g., homomorphic encryption, Shamir’s secret sharing) so that the server can only observe the sum of client updates, not any individual update. Google’s protocol, proposed in Practical Secure Aggregation for Privacy Preserving Machine Learning by Bonawitz et al. (2017).

  • Anomaly Detection: Apply outlier detection or robust aggregation (e.g., median, trimmed mean, Krum) to defend against poisoned or adversarial updates.

Tooling & Frameworks

  • Flower: Flexible framework supporting simulation and real-world deployment, compatible with PyTorch, TensorFlow, JAX.
  • FATE: Industrial-grade system supporting hetero‑FL, secure computation, and cross‑silo scenarios.
  • TensorFlow Federated: Google’s research library integrating TF models into FL workflows.
  • PySyft: Privacy-preserving framework supporting FL, DP, and encrypted ML pipelines.

LLM-Specific Enhancements

  • LoRA-based Fine-Tuning: Reduces communication and computation by 10×–100×. Each client only updates and shares adapter weights (e.g., <1% of full model).

  • Client Selection & Ranking: Clients are often selected based on availability, compute, network, and data quality. Ranking heuristics (e.g., data diversity scores) can further improve convergence.

  • Personalization Layers: Clients can locally adapt final model layers post-FL (e.g., bias or head-only fine-tuning) for user-specific performance while still contributing to a shared global backbone.

Federated Adaptation with LoRA

  • One of the most effective strategies for scalable, privacy-preserving fine-tuning in FL is the use of Low-Rank Adaptation (LoRA). Instead of updating the full parameter set of a large model (which is communication- and memory-intensive), LoRA introduces lightweight trainable matrices that approximate updates in a low-rank subspace.
  • This section elaborates on how LoRA and its variants enable efficient federated fine-tuning for LLMs.

What is Federated LoRA?

  • In Federated LoRA, each client receives a frozen copy of the global LLM and fine-tunes only the inserted low-rank matrices \(A\) and \(B\) at specific layers:

    \[\Delta W \approx A B \quad \text{where } A \in \mathbb{R}^{d \times r},\ B \in \mathbb{R}^{r \times k}\]

  • These low-rank updates (\(AB\)) are then communicated back to the central server, drastically reducing bandwidth and memory usage.

  • Advantages:

    • 10×–100× fewer parameters shared per client.
    • Easily pluggable into existing LLMs (e.g., GPT, BERT, LLaMA).
    • Empirically shown to converge well even under client heterogeneity.

LoRA in Federated Context

  • Federated LoRA Workflow:

    1. Server distributes frozen base model and LoRA config (e.g., rank \(r\), init values).
    2. Clients fine-tune LoRA adapters locally on their data.
    3. Clients send only the LoRA parameters \(\theta_A, \theta_B\) to the server.
    4. Server aggregates adapters and updates the global model (or broadcasts updated adapters).

  • Security:

    • LoRA matrices are much smaller, reducing exposure in the event of leaks.
    • Combine with secure aggregation or differential privacy for formal guarantees.

Open Challenges

  • Heterogeneous adapter ranks: Clients with different compute budgets may choose different ranks, destabilizing aggregation.

  • Partial participation: Aggregation of sparse LoRA updates needs careful design to avoid overfitting to overrepresented clients.

  • Adapter merging: When merging LoRA adapters into the base model post-FL, special care must be taken to balance global and client-specific knowledge.

Pros & Cons

Pros

  • Parameter-efficient fine-tuning: All LoRA-based techniques (LoRA, QLoRA, QA-LoRA, LQ-LoRA) fine-tune only a small set of low-rank parameters, making them ideal for FL environments with limited bandwidth.

  • Adaptable to quantization settings: LoRA variants like QLoRA and QA-LoRA support aggressive quantization (e.g., 4-bit), allowing fine-tuning with reduced memory and compute requirements—especially valuable in client-side FL scenarios.

  • Scalable across clients: Clients send only adapter weights (\(A, B\)) rather than full models, reducing communication costs by over 90%. This makes federated tuning feasible even on mobile devices.

  • Privacy-enhancing: By avoiding transmission of full model weights, and optionally combining with DP-FL, LoRA-based fine-tuning helps achieve stronger privacy guarantees.

  • Accuracy retention: LQ-LoRA and QA-LoRA correct quantization-induced degradation via low-rank compensation, maintaining fidelity even at 4-bit or 2-bit precision.

Cons

  • Hyperparameter sensitivity: LoRA’s performance depends on careful tuning of the rank \(r\), learning rate, and initialization. This gets harder in FL settings with diverse clients.

  • Adapter coordination: Clients may use different adapter ranks or sparsity patterns, which complicates aggregation of LoRA updates.

  • Quantization complexity: Variants like LQ-LoRA and QA-LoRA introduce additional steps—e.g., quantizer calibration, activation scaling—which increase implementation burden.

  • Stability under heterogeneity: In FL, device-specific data distributions may lead to divergent adapter updates, especially for QLoRA and LQ-LoRA. Robust aggregation (e.g., FedProx, FedDyn) is needed.

Comparison & Use Cases

Use Case Suggested Strategy Benefit
Parameter-efficient tuning LoRA / QLoRA / QA-LoRA Reduces compute/memory footprint
Extreme quantization LQ‑LoRA or QA-LoRA 4‑bit or 2‑bit tuning with minimal accuracy loss
Federated fine‑tuning Federated LoRA / QLoRA adapters Minimal communication cost
Quantization-aware training QA‑LoRA + QAT Activations + weights in int4 with recovery via low-rank correction
Memory-constrained fine-tuning QLoRA GPU VRAM usage reduced via paged optimizers + quantized base model
Private on-device personalization QLoRA + DP-FL Combines quantization, privacy, and adapter sharing

Technical Limitations

  • FL systems face several practical limitations:

    • Frequent communication overhead during training rounds.
    • Need for sufficient memory and compute on client devices.
    • Unreliable or low-bandwidth network connections on devices like smartphones or IoT hardware.
    • Loss of updates due to client dropout or communication failures.

  • Statistical and operational challenges include:

    • Heterogeneous and evolving local datasets (e.g., temporal drift).
    • Biased client distributions leading to skewed global models.
    • Limited or missing labels on clients.
    • Difficulty identifying and mitigating global bias without full data access.
    • Risk of adversarial participation and backdoor injection via model updates.

  • Designing robust FL protocols requires anticipating such edge cases and implementing countermeasures like anomaly detection, secure aggregation, or differential privacy.

  • Moreover, decentralized settings complicate synchronization and make fault recovery and consensus more difficult.

Advantages

Privacy

  • The main advantage of using federated approaches to machine learning is to ensure data privacy or data secrecy. Indeed, no local data is uploaded externally, concatenated or exchanged. Since the entire database is segmented into local bits, this makes it more difficult to hack into it.

  • With FL, only machine learning parameters are exchanged. In addition, such parameters can be encrypted before sharing between learning rounds to extend privacy and homomorphic encryption schemes can be used to directly make computations on the encrypted data without decrypting them beforehand. Despite such protective measures, these parameters may still leak information about the underlying data samples, for instance, by making multiple specific queries on specific datasets. Querying capability of nodes thus is a major attention point, which can be addressed using differential privacy and secure aggregation.

  • It was found that the privacy issues of FL is often due to running estimates, which hinders the usage of advanced deep learning models.

A Static Batch Normalization (sBN) for optimizing privacy constrained deep neural networks was developed. During the training phase, sBN does not track running estimates but simply normalizes batch data. Only the statistics of hidden representations from local data after the model converges are calculated. This method is suitable for the FL framework as local models do not need to upload running estimates during training. Local models only upload their statistics once after optimization, which significantly reduces data leakage risk.

Personalization

  • The generated model delivers insights based on the global patterns of nodes. However, if a participating node wishes to learn from global patterns but also adapt outcomes to its peculiar status, the FL methodology can be adapted to generate two models at once in a multi-task learning framework. In addition, clustering techniques may be applied to aggregate nodes that share some similarities after the learning process is completed. This allows the generalization of the models learned by the nodes according also to their local data.

In the case of deep neural networks, it is possible to share some layers across the different nodes and keep some of them on each local node. Typically, first layers performing general pattern recognition are shared and trained all datasets. The last layers will remain on each local node and only be trained on the local node’s dataset.

  • Early personalization methods often introduce additional computation and communication overhead that may not be necessary. To significantly reduce computation and communication costs in FL, a “Masking Trick” approach was developed. The “Masking Trick” allows local clients to adaptively contribute to the training of global models much more flexibly and efficiently compared with classical FL.
  • Western legal frameworks emphasize more and more on data protection and data traceability. The White House 2012 Report recommended the application of a data minimization principle, which is mentioned in European GDPR. In some cases, it is illegal to transfer data from a country to another (e.g., genomic data), however international consortia are sometimes necessary for scientific advances. In such cases FL brings solutions to train a global model while respecting security constraints.

Use cases

  • FL typically applies when individual actors need to train models on larger datasets than their own, but cannot afford to share the data in itself with others (e.g., for legal, strategic or economic reasons). The technology yet requires good connections between local servers and minimum computational power for each node.

Transportation: self-driving cars

  • Self-driving cars encapsulate many machine learning technologies to function: computer vision for analyzing obstacles, machine learning for adapting their pace to the environment (e.g., bumpiness of the road). Due to the potential high number of self-driving cars and the need for them to quickly respond to real world situations, traditional cloud approach may generate safety risks. FL can represent a solution for limiting volume of data transfer and accelerating learning processes.

Industry 4.0: smart manufacturing

  • In Industry 4.0, there is a widespread adoption of machine learning techniques to improve the efficiency and effectiveness of industrial process while guaranteeing a high level of safety. Nevertheless, privacy of sensitive data for industries and manufacturing companies is of paramount importance. FL algorithms can be applied to these problems as they do not disclose any sensitive data. In addition, FL also implemented for PM2.5 prediction to support Smart city sensing applications.

Medicine: digital health

  • FL seeks to address the problem of data governance and privacy by training algorithms collaboratively without exchanging the data itself. Today’s standard approach of centralizing data from multiple centers comes at the cost of critical concerns regarding patient privacy and data protection. To solve this problem, the ability to train machine learning models at scale across multiple medical institutions without moving the data is a critical technology.
  • Nature Digital Medicine published the paper “The Future of Digital Health with Federated Learning” in September 2020, in which the authors explore how FL may provide a solution for the future of digital health, and highlight the challenges and considerations that need to be addressed.
  • Recently, a collaboration of 20 different institutions around the world validated the utility of training AI models using FL.
  • In a paper published in Nature Medicine “Federated learning for predicting clinical outcomes in patients with COVID-19”, they showcased the accuracy and generalizability of a federated AI model for the prediction of oxygen needs in patients with COVID-19 infections.
  • Furthermore, in a published paper “A Systematic Review of Federated Learning in the Healthcare Area: From the Perspective of Data Properties and Applications”, the authors trying to provide a set of challenges on FL challenges on medical data-centric perspective.

Further Reading

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledFederatedLearning,
  title   = {Federated Learning},
  author  = {Chadha, Aman},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}