Primers • F-Beta Score
\(F_\beta\) Score
-
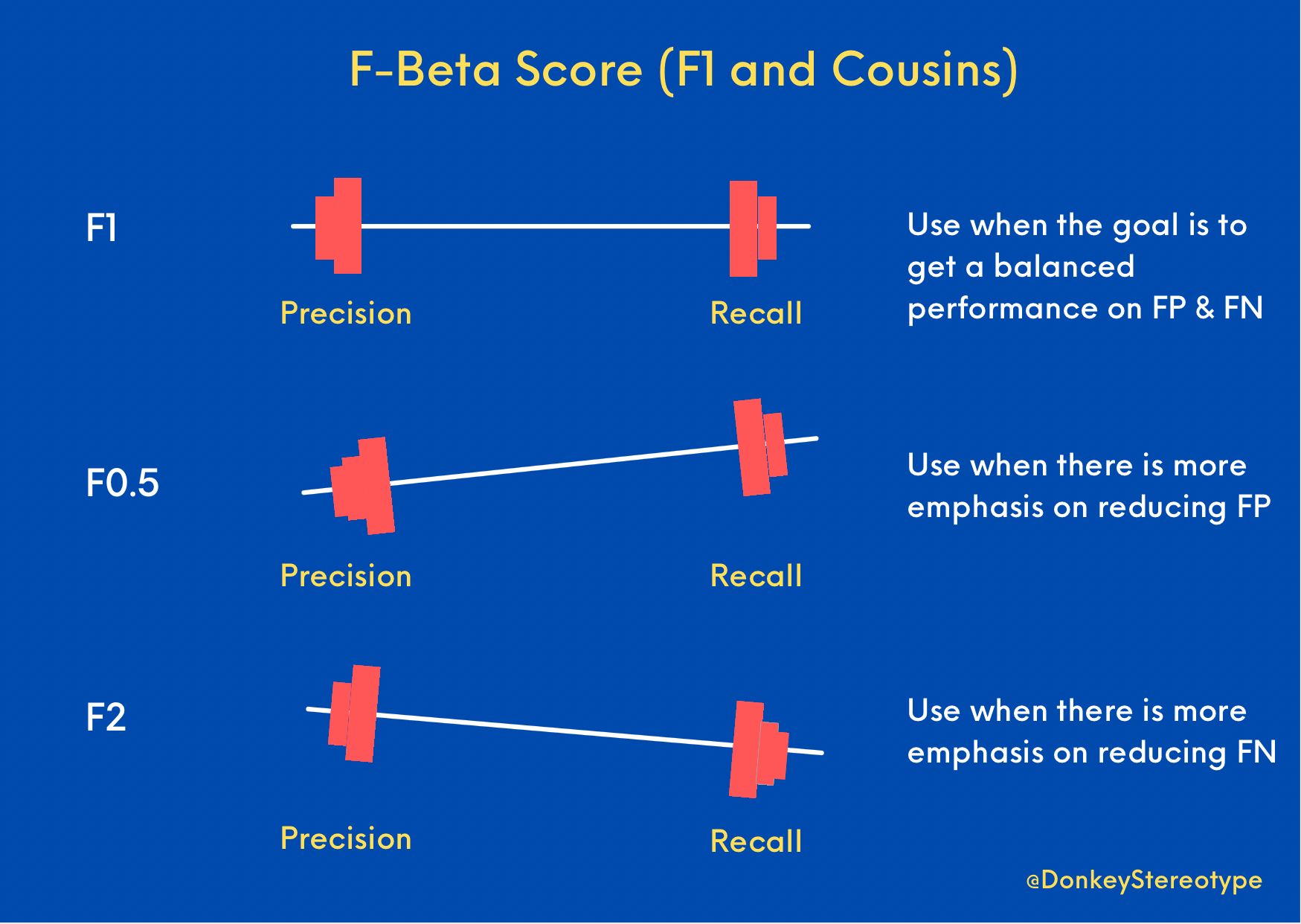
\(F_\beta\) score is the generalization of what people loosely call as \(F_1\) score, which is a harmonic mean of precision and recall. \(F_1\) is nothing but \(F_\beta\) with \(\beta = 1\), where precision and recall are given equal weightage. The beta parameter determines the weight of recall in the combined score. \(\beta < 1\) lends more weight to precision, while \(\beta > 1\) favors recall (\(\beta \rightarrow 0\) considers only precision, \(\beta \rightarrow +\infty\) only recall).
-
We use \(F_1\) when we want to strike a balance on getting an optimum False Positives and optimum False Negatives. What if we want to weigh them differently? The answer is \(F_{0.5}\) and \(F_{2.0}\), the two siblings of the \(F_1\) score.
-
\(F_{0.5}\) is \(F_\beta\) with \(\beta = 0.5\), which is needed when you want to weigh precision more than recall. Why? You need this when your end goal is to reduce False Positives (FP). For e.g., child safety detector for social media content. In this case, even one FP could be disastrous, so optimizing for an FP that is a theoretical zero makes sense.
-
\(F_{2.0}\) is \(F_\beta\) with \(\beta = 2.0\), which is needed when you want to weigh recall more than precision. Why? You need this when your end goal is to reduce False Negatives (FN). For e.g., rare cancer detector. In this case, an FN i.e. failing to catch a rare cancer for a patient who actually has it is disastrous. We are even better off having a higher rate of FPs here because when diagnosed with a rare cancer people tend to get a second checkup/opinion but if you clear them in the 1st test they naturally don’t test again to verify.
-
The diagram below from Prithvi Da summarizes the aforementioned metrics.
References
Further Reading
Citation
If you found our work useful, please cite it as:
@article{Chadha2020DistilledKernelTrick,
title = {Kernel Trick},
author = {Chadha, Aman},
journal = {Distilled AI},
year = {2020},
note = {\url{https://aman.ai}}
}