Primers • Differential Privacy
Background
- Differential privacy (DP) is a system for publicly sharing information about a dataset by describing the patterns of groups within the dataset while withholding information about individuals in the dataset. The idea behind differential privacy is that if the effect of making an arbitrary single substitution in the database is small enough, the query result cannot be used to infer much about any single individual, and therefore provides privacy.
- Another way to describe differential privacy is as a constraint on the algorithms used to publish aggregate information about a statistical database which limits the disclosure of private information of records whose information is in the database.
- For example, differentially private algorithms are used by some government agencies to publish demographic information or other statistical aggregates while ensuring confidentiality of survey responses, and by companies to collect information about user behavior while controlling what is visible even to internal analysts.
- Roughly, an algorithm is differentially private if an observer seeing its output cannot tell if a particular individual’s information was used in the computation. Differential privacy is often discussed in the context of identifying individuals whose information may be in a database. Although it does not directly refer to identification and reidentification attacks, differentially private algorithms probably resist such attacks.
- Differential privacy was developed by cryptographers and thus is often associated with cryptography, and draws much of its language from cryptography.
Privacy budget
- A typical differential privacy implementation incorporates the concept of a per-donation privacy budget (quantified by the parameter \(\epsilon\)), and sets a strict limit on the number of contributions from a user in order to preserve their privacy. The reason is that the slightly-biased noise used in differential privacy tends to average out over a large numbers of contributions, making it theoretically possible to determine information about a user’s activity over a large number of observations from a single user (though it’s important to note that we don’t associate any identifiers with information collected using differential privacy).
- Local differential privacy to help protect the privacy of user activity in a given time period, while still gaining insight that improves the intelligence and usability of the system’s features.
- From Apple Differential Privacy Technical Overview, as an example, Apple utilizes differential privacy for the following features:
- QuickType suggestions
- Emoji suggestions
- Lookup Hints
- Safari Energy Draining Domains
- Safari Autoplay Intent Detection (macOS High Sierra)
- Safari Crashing Domains (iOS 11)
- Health Type Usage (iOS 10.2)
- For each feature, Apple seeks to make the privacy budget small while still collecting enough data to to enable Apple to improve features. Apple retains the collected data for a maximum of three months. The donations do not include any identifier, and IP addresses are not stored.
- For Lookup Hints, Apple uses a privacy budget with epsilon of 4, and limits user contributions to two donations per day.
- For emoji, Apple uses a privacy budget with epsilon of 4, and submits one donation per day.
- For QuickType, Apple uses a privacy budget with epsilon of 8, and submits two donations per day.
- For Health types, Apple uses a privacy budget with epsilon of 2 and limits user contributions to one donation per day. The donations do not include health information itself, but rather which health data types are being edited by users.
- For Safari, Apple limits user contributions to 2 donations per day. For Safari domains identified as causing high energy use or crashes, Apple uses a single privacy budget with epsilon of 4.
- For Safari Auto-play intent detection, Apple uses a privacy budget with an \(\epsilon\) of 8.
- Referring to the histogram below (source), the Count Mean Sketch technique allows Apple to determine the most popular emoji to help design better ways to find and use our favorite emoji. The top emoji for US English speakers contained some surprising favorites.
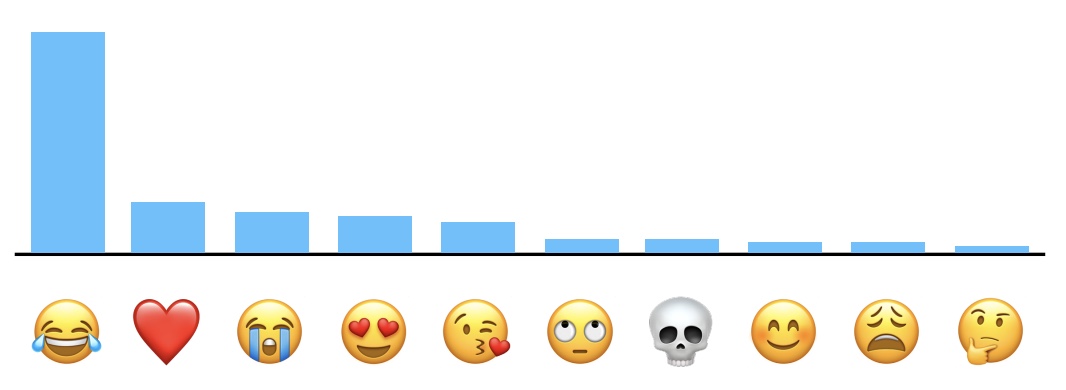
Techniques
- Local differential privacy guarantees that it is difficult to determine whether a certain user contributed to the computation of an aggregate by adding slightly biased noise to the data that is shared. But before adding this noise, it’s necessary to define a data structure that captures a sketch of user input with a small number of bits.
- Two common techniques are typically utilized:
Count Mean Sketch
- In our use of the Count Mean Sketch technique for differential privacy, the original information being processed for sharing with Apple is encoded using a series of mathematical functions known as hash functions, making it easy to represent data of varying sizes in a matrix of fixed size.
- The data is encoded using variations of a SHA-256 hash followed by a privatization step and then written into the sketch matrix with its values initialized to zero.
- The noise injection step works as follows: After encoding the input as a vector using a hash function, each coordinate of the vector is then flipped (written as an incorrect value) with a probability of \(\frac{1}{1 + e^{\frac{\epsilon}{2}}}\), where \(\epsilon\) is the privacy parameter. This assures that analysis of the collected data cannot distinguish actual values from flipped values, helping to assure the privacy of the shared information.
- In order to stay within the privacy budget we do not send the entire sketch matrix to the server but only a random row of the matrix. When the information encoded in the sketch matrix is sent to Apple, the Apple server tallies the responses from all devices sharing information and outputs the mean value for each element of the array.
- Although each submission contains many randomized elements, the average value across large numbers of submissions gives Apple meaningful aggregate data.
Hadamard Count Mean Sketch
- The Hadamard Count Mean–based Sketch technique uses a noise injection method similar to the one used in the Count Mean Sketch technique, but with an important difference: It applies a type of mathematical operation called a Hadamard basis transformation to the hashed encoding before performing the privatization step.
- Additionally, it samples only 1 bit at random to send instead of the entire row as in the Count Mean Sketch technique. This reduces communication cost to 1 bit at the expense of some accuracy.
Further Reading
Citation
If you found our work useful, please cite it as:
@article{Chadha2020DistilledDifferentialPrivacy,
title = {Differential Privacy},
author = {Chadha, Aman},
journal = {Distilled AI},
year = {2020},
note = {\url{https://aman.ai}}
}