Overview

  • On-device AI, also known as edge computing, processes data directly on the user’s device—like a smartphone or tablet—rather than sending it to a centralized server. This architecture significantly enhances privacy and security, since user data remains on the device, reducing the risk of exposure during transmission or on external servers. In applications like natural language processing and large language models, where conversations often involve sensitive or personal information, local processing ensures that this data never leaves the user’s control.

  • However, deploying AI models on devices with limited computational resources presents challenges. Innovations in model compression, such as pruning and quantization, are making it increasingly feasible to run powerful yet efficient models on-device.

  • Differential privacy (DP) complements this approach by providing a mathematical guarantee that individual user data cannot be reverse-engineered from aggregate outputs. Even when data must be collected or analyzed—say, to improve model performance—DP ensures that the influence of any single user is indistinguishable. This means algorithms constrained by differential privacy can reveal patterns in user behavior without revealing any one person’s actions or identity.

  • Originally developed by cryptographers, differential privacy has become a foundation for responsible data use. When combined with on-device AI, it supports a robust privacy-preserving paradigm: sensitive computations happen locally, and any aggregate data used for model updates or analytics adheres to strict privacy constraints. Together, on-device processing and differential privacy offer a compelling path toward secure, trustworthy AI.

Background

  • In modern machine learning systems, models are frequently trained on sensitive user data—medical records, financial transactions, browsing histories, and more. While these models can achieve high utility, they may unintentionally memorize and leak private information. For instance, a language model trained on private emails might reveal exact sentences from those emails when prompted a certain way.

  • Differential Privacy (DP) is a rigorous mathematical framework designed to mitigate such privacy risks. The goal is to ensure that no single individual’s data has a significant impact on the model’s output—making it extremely difficult for an adversary to infer whether any particular user’s data was included in the training set. This enables organizations to share insights from data without compromising the confidentiality of individuals.

  • The key motivation is to achieve a balance between utility and privacy:

    • How can we allow models to learn useful patterns across data…
    • …without overfitting to, or memorizing, individual data points?

  • DP provides quantitative guarantees against membership inference, model inversion, and other forms of privacy attacks—backed by formal statistical theory.

  • Roughly, an algorithm is differentially private if an observer seeing its output cannot tell if a particular individual’s information was used in the computation. Differential privacy is often discussed in the context of identifying individuals whose information may be in a database. Although it does not directly refer to identification and reidentification attacks, differentially private algorithms probably resist such attacks.

  • Differential privacy was developed by cryptographers and is thus often associated with cryptography, drawing much of its language and foundations from it.

Privacy Budget and Definition

  • A randomized algorithm \(M\) (such as a learning algorithm or query mechanism) is said to satisfy \((\varepsilon, \delta)\)-differential privacy if for any two adjacent datasets \(D\) and \(D'\)—that differ by only a single record—and for all measurable subsets of possible outputs \(S \subseteq \text{Range}(M)\), the following holds:
\[\Pr[M(D) \in S] \leq e^\varepsilon \cdot \Pr[M(D') \in S] + \delta\]

Components

  • \(\varepsilon\) (epsilon): The privacy loss parameter. Smaller values imply stronger privacy. A typical range is \(\varepsilon \in [0.01, 10]\).
  • \(\delta\): The probability that the differential privacy guarantee fails. Typically chosen to be smaller than \(\frac{1}{n}\), where \(n\) is the dataset size.
  • Adjacent datasets: Two datasets are adjacent if they differ in exactly one individual’s data.
  • Randomized algorithm \(M\): The core of DP is randomness—achieved by injecting carefully calibrated noise (e.g., Laplace or Gaussian)—so that individual records cannot be inferred from outputs.

Intuition

  • This definition ensures that the presence or absence of a single user’s data does not significantly influence the output distribution of the algorithm. Even a powerful adversary cannot confidently determine if a specific user contributed data, based on the output alone.

Tightness

  • If \(\delta = 0\), we get pure differential privacy.
  • If \(\delta > 0\), the guarantee becomes approximate differential privacy, which is more practical for complex models like deep neural networks.

Privacy Budget in Practice

  • A typical differential privacy system tracks a user’s privacy budget—a measure of how much information about them has been exposed.
  • The budget is often enforced by setting limits on the number of contributions per user and how much noise is injected.

Real-World Example: Apple DP

  • From Apple’s Differential Privacy Technical Overview, Apple uses carefully bounded \(\varepsilon\) values and per-day contribution limits to collect aggregate insights without compromising user privacy. Examples include:

    • Emoji suggestions: \(\varepsilon = 4\), one contribution per day.
    • QuickType: \(\varepsilon = 8\), two donations per day.
    • Safari Auto-play intent detection: \(\varepsilon = 8\), two donations per day.
    • Health Type Usage: \(\varepsilon = 2\), one donation per day (only metadata, not raw health info).

  • These limits and budgets are designed to keep user-specific data unidentifiable—even internally.

Example Visualization (Apple DP Emoji Analysis)

  • Apple uses techniques like Count Mean Sketch to estimate popular emoji in a privacy-preserving way. Here’s an example histogram shared in their technical whitepaper:

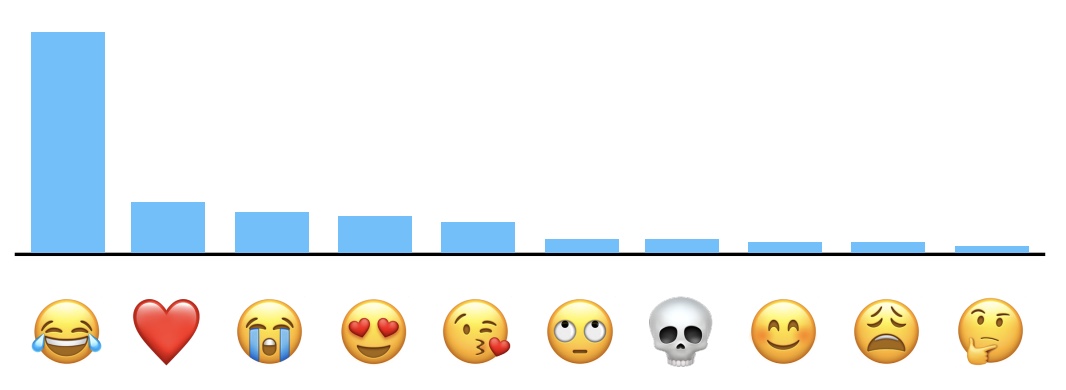
  • This visual illustrates how even noisy, privacy-preserving data collection can yield useful aggregate insights.

Techniques

  • To implement differential privacy in practice, especially under the local differential privacy (LDP) model, one must design mechanisms that apply randomized noise directly to the user’s data before it leaves their device. These mechanisms require specialized data representations and noise injection strategies that strike a balance between privacy protection and statistical utility.

  • Two widely used LDP techniques for structured telemetry data are as follows.

Count Mean Sketch (CMS)

  • This technique creates a sketch matrix to represent user inputs compactly.
  • Data is hashed using functions like SHA-256 to discretize inputs into vectors.
  • Each coordinate of the hashed vector is then flipped with probability:
\[\frac{1}{1 + e^{\varepsilon / 2}}\]
  • This flipping introduces uncertainty, so the server cannot tell whether any specific bit was the result of a user’s actual data or the added noise.

Workflow

  • The workflow for CMS is as follows:

    1. User input is hashed and mapped into a vector space.
    2. The vector is privatized using random flips.
    3. Only one random row of the sketch matrix is transmitted to the server to further reduce information leakage.
    4. The server aggregates noisy vectors from many users and averages them, estimating population-level statistics (e.g., the most common emojis or words).

  • This setup provides good privacy with moderate utility, especially over large user populations.

Hadamard Count Mean Sketch (HCMS)

  • A refinement over CMS, the HCMS adds a Hadamard basis transformation to the vector before privatization.

  • After this transformation:

    • Only a single bit is sampled and transmitted to the server per query.
    • This reduces communication cost to just 1 bit per user per record, at the cost of slightly reduced accuracy.

Advantages

  • More efficient in bandwidth-constrained settings (e.g., mobile devices).

  • Useful for telemetry collection at scale, where millions of users contribute daily.

  • Both techniques are used to power Apple’s differential privacy systems, as seen in their emoji, QuickType, and Safari data collection pipelines.

DP‑SGD and Implementation

  • When applying differential privacy to deep learning models—particularly for training large neural networks—a widely adopted approach is Differentially Private Stochastic Gradient Descent (DP‑SGD).

DP‑SGD: Core Idea

  • The standard stochastic gradient descent (SGD) algorithm is modified to ensure that updates do not leak private information. This is done by controlling the sensitivity of each training step via two key operations:

  1. Gradient Clipping:

    • For each training example, compute the per-sample gradient.

    • Clip the gradient to a fixed maximum norm \(C\):

      \[g_i \leftarrow g_i \cdot \min\left(1, \frac{C}{\|g_i\|_2}\right)\]

  2. Noise Addition:

    • After averaging the clipped gradients, add Gaussian noise:

      \[\bar{g} = \frac{1}{n} \sum_i g_i + N(0, \sigma^2 C^2 \mathbf{I})\]

    • Here, \(\sigma\) is the noise multiplier that controls the privacy-utility trade-off.

  3. Privacy Tracking:

    • A privacy accountant (such as Rényi or Moments Accountant) keeps track of the cumulative privacy loss \(\varepsilon\) throughout training.

PyTorch Implementation with Opacus

  • Facebook’s Opacus library makes it easy to implement DP‑SGD in PyTorch with minimal code changes:
from opacus import PrivacyEngine

privacy_engine = PrivacyEngine(
    model,
    batch_size=256,
    sample_size=len(dataset),
    noise_multiplier=1.2,
    max_grad_norm=1.0
)
privacy_engine.attach(optimizer)
  • max_grad_norm defines the clipping threshold \(C\).
  • noise_multiplier corresponds to \(\sigma\).
  • Opacus automatically modifies the model to track per-sample gradients, apply clipping and noise, and track \(\varepsilon\) across epochs.

DP‑Weights (Post-training Differential Privacy)

  • An alternative to DP‑SGD is DP‑Weights, where noise is added after training:

    \[\theta^\text{private} = \theta^\text{trained} + N(0, \sigma^2 I)\]

  • This is helpful when retraining is expensive, as it provides some privacy protection with lower overhead.

  • While not as strong as full DP‑SGD, it still prevents exact memorization of individual training records and can mitigate simple membership inference attacks.

Application to LLMs & NLP

  • Applying differential privacy to large language models (LLMs) and NLP tasks introduces both opportunities and challenges. These models are often trained on massive datasets that may contain sensitive personal information (emails, messages, medical notes, etc.), making them natural candidates for differential privacy.

Fine-Tuning with DP-SGD

When fine-tuning pre-trained LLMs on private datasets (e.g., clinical corpora or enterprise emails), the DP-SGD algorithm can be directly applied to protect individual data points. The typical pipeline involves:

  1. Privacy Parameter Selection:

    • Choose an acceptable privacy budget \(\varepsilon\) and failure probability \(\delta\).
    • Common settings in literature: \(\varepsilon = 1\) to \(10\), \(\delta = 10^{-5}\) to \(10^{-8}\).

  2. Hyperparameter Calibration:

    • Tune gradient clipping norm \(C\), noise multiplier \(\sigma\), batch size, and learning rate.
    • Use a calibration set (non-sensitive) to test different combinations that optimize accuracy under a fixed privacy budget.

  3. Training and Privacy Accounting:

    • Train the model using DP-SGD (e.g., via Opacus), and track the total privacy loss across epochs.
    • Use moments accountant or Rényi differential privacy accountant for tighter analysis of cumulative \(\varepsilon\).

  4. Model Evaluation:

    • Evaluate utility trade-off: privacy often comes at the cost of increased perplexity or reduced BLEU/F1 scores in NLP tasks.
    • Trade-off improves with larger public pretraining and private fine-tuning.

Membership Inference & Protection

  • Differential privacy is particularly effective at mitigating membership inference attacks—where an attacker queries a model and tries to determine whether specific records were part of its training set.
  • In NLP, these attacks are especially potent: LLMs can memorize rare sequences (e.g., uncommon names or numbers), which attackers can prompt into being reproduced.
  • DP-trained models are less likely to memorize such outliers, improving privacy robustness in deployment.

Recent Strategies

  • Pre-train with DP, fine-tune with public data:

    • Train a model under strong DP constraints (e.g., on private corpora).
    • Fine-tune on open-domain datasets (e.g., Wikipedia, C4) to recover utility without additional privacy cost.

  • Public target-tuning:

    • Fine-tune a public model on public data to a target task.
    • Use DP-SGD on private examples only to adapt the model (e.g., via LoRA adapters) while preserving privacy.

Pros & Cons

  • DP introduces formal privacy protections into machine learning pipelines but comes with practical trade-offs. Here’s a look at its strengths and limitations.

Pros

  • Formal Privacy Guarantees: DP provides mathematically provable bounds on the risk of individual data exposure—offering strong defense against attacks like membership inference and data reconstruction.

  • Tooling Ecosystem: Libraries like Opacus (PyTorch) and TensorFlow Privacy streamline DP integration with deep learning models, supporting gradient clipping, noise addition, and privacy accounting.

  • General Applicability: Can be applied to various components: model training (via DP-SGD), post-training (via DP-Weights), or user-level contributions (via local DP mechanisms).

  • Defends Against Real-World Threats: Especially valuable in medical, financial, or sensitive NLP domains where privacy breaches can have serious consequences.

Cons

  • Utility Degradation: Injecting noise during training often leads to higher perplexity, lower F1 scores, or degraded generation quality—especially for smaller datasets or tasks requiring fine detail.

  • Complex Hyperparameter Tuning: Requires careful balancing of noise multiplier, clipping norms, batch sizes, and learning rate. Poor tuning can nullify either privacy or utility.

  • Privacy Budget Exhaustion: Each training epoch and query consumes part of the privacy budget \(\varepsilon\); long training or frequent evaluations can accumulate privacy loss quickly.

  • Scalability Concerns: Computing per-sample gradients (needed for DP-SGD) is computationally expensive, especially for large LLMs.

  • Task Sensitivity: Some NLP tasks (e.g., rare token generation, open-ended dialogue) are more vulnerable to degradation under DP due to their reliance on nuanced memorization.

Further Reading

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledDifferentialPrivacy,
  title   = {Differential Privacy},
  author  = {Chadha, Aman},
  journal = {Distilled AI},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}