Primers • Activation Functions
Overview
- The idea behind activation functions ‘s use an example. Let’s say you are working in a car parts manufacturing company as a quality control operator. Your job is to test each part coming out of the machine against the quality standards, and if the part is up to the mark, you send the part to the next stage. If not, either you discard it or label it for a further touch-up.
- Now, what would happen if the quality control operator was not there? Every part coming out of the machine is going to move to the next stage. What if that part is the car brakes? In this scenario, you would be getting a car with brakes that have never been tested for quality standards. No one would ever want a car like that! Would you?
- Activation functions work just like a quality control operator. They check the output of every neuron before pushing it forward to the next layer or neuron. If there is no activation function, then you simply get a linear model as a result, which we don’t want, because if we want a linear model, then linear regression should be enough. Why bother with neural networks at all?
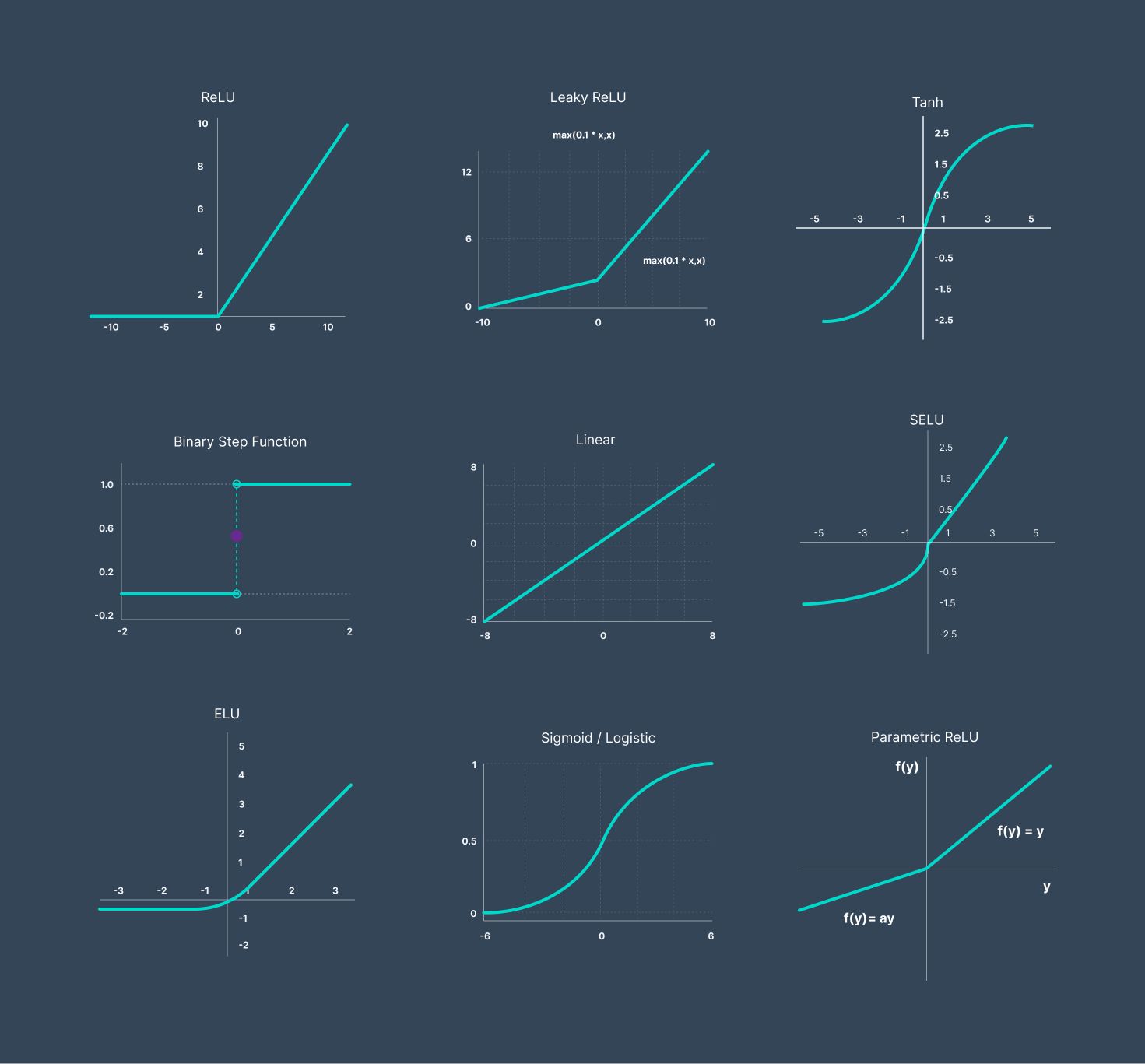
- As an example of the ReLU function as an activation function, which lets the output of a neuron pass as it is to the next layer if its value is bigger than zero, but if it is less or equal to zero, then it makes the output of the neuron zero and pushes that zero forward. This adds non-linearity to the linear output from the neuron, and this is what makes neural networks shine.
Types of Activation Functions
- Let’s go over the different activation functions that we can use in different scenarios.
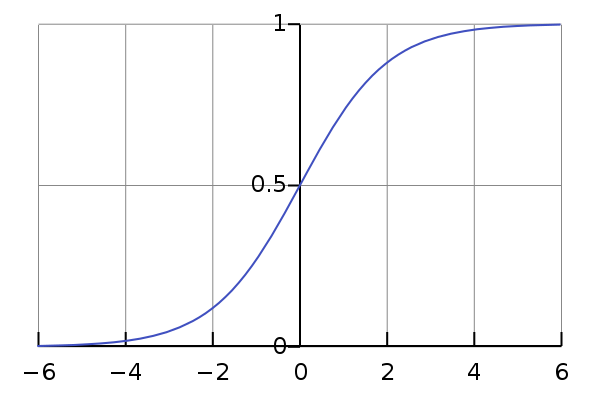
Sigmoid
- The Sigmoid function is used for binary classification. It squashes a vector in the range (0, 1). It is applied independently to each element of \(s\). It is also called the logistic function (since it is used in logistic regression for binary classification).
Pros
- Utilized in binary classification.
- Offers an output that can be interpreted as a probability value since it is non-negative and in the range (0, 1).
Softmax
- The Softmax function is a generalization of the sigmoid function for multi-class classification. In other words, use sigmoid for binary classification and softmax for multiclass classification. Softmax is a function, not a loss. It squashes a vector in the range (0, 1) and all the resulting elements sum up to 1. It is applied to the output scores \(s\). As elements represent a class, they can be interpreted as class probabilities.
-
The Softmax function cannot be applied independently to each \(s_i\), since it depends on all elements of \(\boldsymbol{s}\). For a given class \(s_i\), the Softmax function can be computed as:
\[f(s)_i=\frac{e^{s_i}}{\sum_j^C e^{s_j}}\]- where \(s_j\) are the scores inferred by the net for each class in \(C\). Note that the Softmax activation for a class \(s_i\) depends on all the scores in \(s\).
- Activation functions are used to transform vectors before computing the loss in the training phase. In testing, when the loss is no longer applied, activation functions are also used to get the CNN outputs.
Pros
- Utilized in multi-class classification.
ReLU (Rectified Linear Unit)
Pros
- Due to sparsity, there is less time and space complexity compared to the sigmoid.
- Avoids the vanishing gradient problem.
Cons
- Introduces the concept of the “dead ReLU problem,” which refers to network elements that are probably never updated with new values. This can also cause issues from time to time. In a way, this is also an advantage.
- Does not avoid the exploding gradient problem.
ELU (Exponential Linear Unit)
Pros
- Avoids the dead ReLU problem.
- Enables the network to nudge weights and biases in the desired directions by producing negative outputs.
- When calculating the gradient, create activations rather than having them be zero.
Cons
- Increases computing time due to the use of an exponential operation.
- Does not avoid the exploding gradient problem.
- The alpha value is not learned by the neural network.
Leaky ReLU (Leaky Rectified Linear Unit)
Pros
- Since we allow a tiny gradient when computing the derivative, we avoid the dead ReLU problem, just like ELU.
- Faster to compute than ELU, because no exponential operation is included.
Cons
- Does not avoid the exploding gradient problem.
- The alpha value is not learned by the neural network.
- When differentiated, it becomes a linear function, whereas ELU is partially linear and partially nonlinear.
SELU (Scaled Exponential Linear Unit)
- If utilized, keep in mind that the LeCun Normal weight initialization approach is necessary for the SELU function and that Alpha Dropout is a unique variant that must be used if dropout is desired.
Pros
- The SELU activation is self-normalizing, hence the neural network converges more quickly than external normalization.
- Vanishing and exploding gradient problems are impossible.
Cons
- Works best for sequential network architectures. If your architecture has skipped connections, self-normalization will not be guaranteed, hence better performance is not guaranteed.
GELU (Gaussian Error Linear Unit)
Pros
- Appears to be cutting-edge in NLP, particularly in Transformer models.
- Avoids vanishing gradient problem
Cons
- Fairly new in practical use, although introduced in 2016.
Citation
If you found our work useful, please cite it as:
@article{Chadha2020DistilledActFunctions,
title = {Activation Functions},
author = {Chadha, Aman and Jain, Vinija},
journal = {Distilled AI},
year = {2020},
note = {\url{https://aman.ai}}
}