Training Neural Networks I

  • As a revision here are the mini-batch stochastic gradient descent algorithm steps:

    • Loop:
      1. Sample a batch of data.
      2. Forward prop it through the graph (network) and get loss.
      3. Backprop to calculate the gradients.
      4. Update the parameters using the gradients.

Activation Functions

  • Different choices for activation function includes Sigmoid, tanh, RELU, Leaky RELU, Maxout, and ELU.

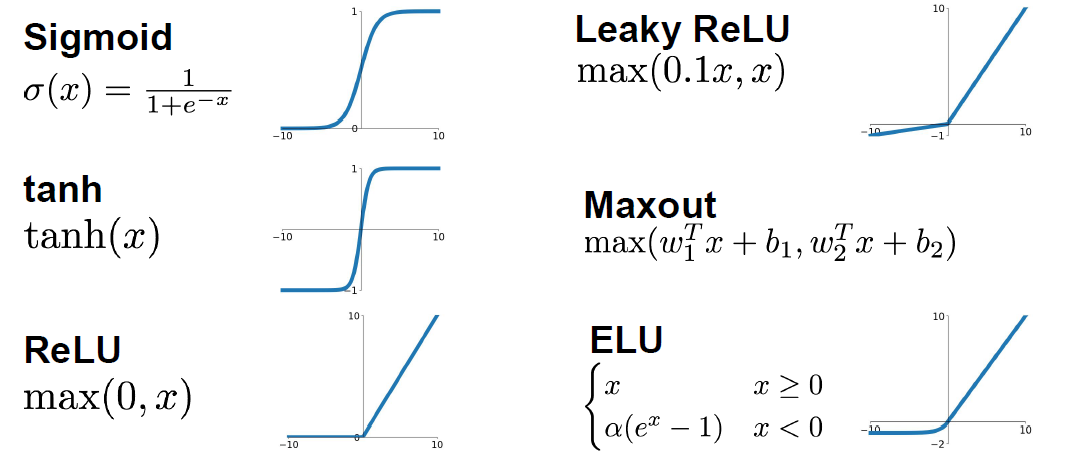
  • Sigmoid:

    • Squashes the numbers between [0,1]
    • Used as a firing rate like human brains.
    \[sigmoid(x) = \frac{1}{(1 + e^-x)}\]
    • Problems with sigmoid:
      • big values neurons kill the gradients.
        • Gradients are in most cases near 0 (Big values/small values), that kills the updates if the graph/network are large.
      • Not Zero-centered.
        • Didn’t produce zero-mean data.
      • exp() is a bit compute expensive.
        • just to mention. We have a more complex operations in deep learning like convolution.

  • tanh:

    • Squashes the numbers between \([-1,1]\).
    • Zero centered.
    • Still big values neurons “kill” the gradients.
    • tanh(x) is the equation.
    • Proposed by Yann LeCun in 1991.

  • RELU (Rectified linear unit):

    • RELU(x) = max(0, x)
    • Doesn’t kill the gradients.
      • Only small values that are killed. Killed the gradient in the half
    • Computationally efficient.
    • Converges much faster than Sigmoid and tanh (6x)
    • More biologically plausible than sigmoid.
    • Proposed by Alex Krizhevsky in 2012 as AlexNet.
    • Problems:
      • Not zero centered.
    • If weights aren’t initialized good, maybe 75% of the neurons will be dead and that’s a waste computation. But its still works. This is an active area of research to optimize this.
    • To solve the issue mentioned above, people might initialize all the biases by 0.01

  • Leaky RELU:

    • leaky_RELU(x) = max(0.01x,x)
    • Doesn’t kill the gradients from both sides.
    • Computationally efficient.
    • Converges much faster than Sigmoid and tanh (6x).
    • Will not die.
    • PRELU is placing the 0.01 by a variable alpha which is learned as a parameter.

  • Exponential linear units (ELU):

    • ELU(x) = { x                               if x > 0
   alpha *(exp(x) -1)                      if x <= 0
   # alpha are a learning parameter
}

    • It has all the benefits of RELU

    • Closer to zero mean outputs and adds some robustness to noise.

    • Problems

      • exp() is a bit compute expensive.

  • Maxout activations:

    • maxout(x) = max(w1.T*x + b1, w2.T*x + b2)
    • Generalizes RELU and Leaky RELU
    • Doesn’t die!
    • Problems:
      • oubles the number of parameters per neuron

  • In practice:

    • Use RELU. Be careful for your learning rates.
    • Try out Leaky RELU/Maxout/ELU
    • Try out tanh but don’t expect much.
    • Don’t use sigmoid!

Data preprocessing

  • Normalize the data:
# Zero centered data. (Calculate the mean for every input).
# On of the reasons we do this is because we need data to be between positive and negative and not all the be negative or positive. 
X -= np.mean(X, axis = 1)

# Then apply the standard deviation. Hint: in images we don't do this.
X /= np.std(X, axis = 1)

  • To normalize images:

    • Subtract the mean image (e.g. AlexNet).
      • Mean image shape is the same as the input images.
    • Or subtract the per-channel mean
      • Means calculate the mean for each channel of all images. Shape is 3 (3 channels)

Weight initialization

  • What happened when initialize all \(W's\) with zeros?

    • All the neurons will do exactly the same thing. They will have the same gradient and they will have the same update.
    • So if W’s of a specific layer is equal the thing described happened

  • First idea is to initialize the \(W's\) with small random numbers:

    W = 0.01 * np.random.rand(D, H)
# Works OK for small networks but it makes problems with deeper networks!

    • The standard deviations is going to zero in deeper networks. and the gradient will vanish sooner in deep networks.

      W = 1 * np.random.rand(D, H) 
# Works OK for small networks but it makes problems with deeper networks!

    • The network will explode with big numbers!

  • Xavier initialization:

      W = np.random.rand(in, out) / np.sqrt(in)

    • It works because we want the variance of the input to be as the variance of the output.

    • But it has an issue, It breaks when you are using RELU.

  • He initialization (Solution for the RELU issue):

    W = np.random.rand(in, out) / np.sqrt(in/2)
    • Solves the issue with RELU. Its recommended when you are using RELU

  • Proper initialization is an active area of research.

Batch normalization

  • is a technique to provide any layer in a Neural Network with inputs that are zero mean/unit variance.
  • It speeds up the training. You want to do this a lot.
    • Made by Sergey Ioffe and Christian Szegedy at 2015.
  • We make a Gaussian activations in each layer. by calculating the mean and the variance.
  • Usually inserted after (fully connected or Convolutional layers) and (before nonlinearity).
  • Steps (For each output of a layer)
    1. First we compute the mean and variance^2 of the batch for each feature.
    2. We normalize by subtracting the mean and dividing by square root of (variance^2 + epsilon)
      • epsilon to not divide by zero
    3. Then we make a scale and shift variables: Result = gamma * normalizedX + beta
      • gamma and beta are learnable parameters.
      • it basically possible to say “Hey! I don’t want zero mean/unit variance input, give me back the raw input - it’s better for me.”
      • Hey shift and scale by what you want not just the mean and variance!
  • The algorithm makes each layer flexible (It chooses which distribution it wants)
  • We initialize the BatchNorm Parameters to transform the input to zero mean/unit variance distributions but during training they can learn that any other distribution might be better.
  • During the running of the training we need to calculate the globalMean and globalVariance for each layer by using weighted average.
  • Benefits of Batch Normalization
    • Networks train faster.
    • Allows higher learning rates.
    • helps reduce the sensitivity to the initial starting weights.
    • Makes more activation functions viable.
    • Provides some regularization.
      • Because we are calculating mean and variance for each batch that gives a slight regularization effect.
  • In conv layers, we will have one variance and one mean per activation map.
  • Batch normalization have worked best for CONV and regular deep NN, But for recurrent NN and reinforcement learning its still an active research area.
    • Its challengey in reinforcement learning because the batch is small.

Baby sitting the learning process

  1. Preprocessing of data.
  2. Choose the architecture.
  3. Make a forward pass and check the loss (disable regularization). Check if the loss is reasonable.
  4. Add regularization, the loss should go up!
  5. Disable the regularization again and take a small number of data and try to train the loss and reach zero loss.
    • You should overfit perfectly for small datasets.
  6. Take your full training data, and small regularization then try some value of learning rate.
    • If loss is barely changing, then the learning rate is small.
    • If you got NAN then your NN exploded and your learning rate is high.
    • Get your learning rate range by trying the min value (that can change) and the max value that doesn’t explode the network.
  7. Do Hyperparameters optimization to get the best hyperparameters values.

Hyperparameter Optimization

  • Try Cross validation strategy.
    • Run with a few epochs, and try to optimize the ranges.
  • Its best to optimize in log space.
  • Adjust your ranges and try again.
  • Better to try random search instead of grid searches (in log space).

Citation

If you found our work useful, please cite it as:

@article{Chadha2020TrainingNeuralNetworksI,
  title   = {Training Neural Networks I},
  author  = {Chadha, Aman},
  journal = {Distilled Notes for Stanford CS231n: Convolutional Neural Networks for Visual Recognition},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}