• Neural networks are widely used to predict. What if they could be used to generate new images, texts or even audio clips?

  • Imagine training a robotic arm to localize objects on a table (in order to grasp them.) Collecting real data for this task is expensive. It requires to position objects on a table, take pictures and label with bounding boxes. Alternatively, taking screenshots in simulations allows you to virtually generate millions of labelled images. The downside is that a network trained on simulated data might not generalize to real data. Having a network that generates real homologues of simulated images would be a game changer. This is one example of application of Generative Adversarial Networks (GANs.)

  • This topic will give you a thorough grounding on GANs and how to apply them to cutting-edge tasks.

Motivation

  • Are networks capable of generating images of cats they have never seen? Intuitively, they should be. If a cat vs. non-cat classifier generalizes to unseen data, it means that it understands the salient features of the data (i.e. what a cat is and isn’t) instead of overfitting the training data. Similarly, a generative model should be able to generate pictures of cats it has never seen because its complexity (~ number of parameters) doesn’t allow it to memorize the training set.

  • For instance, the following cats, cars and faces were generated by Karras et al. 1 using GANs. They do not exist in reality!

The generator vs. discriminator game

  • Although there exist various generative algorithms, this article will focus on the study of GANs.

  • A GAN 2 involves two neural networks. The first network is called the “generator” ($G$) and its goal is to generate realistic samples. The second network is a binary classifier called the “discriminator”, and its goal is to differentiate fake samples (label \(0$) from real sample (label\)1$.)

  • These two networks play a game. \(D\) alternatively receives real samples from a database and fake samples generated by \(G\), and has to learn to differentiate them. At the same time, \(G\) learns to fool \(D$. The game ends when\)G\(generates samples that are realistic enough to fool\)D$. When training ends successfully, you can use \(G\) to generate realistic samples. Here’s an illustration of the GAN game.

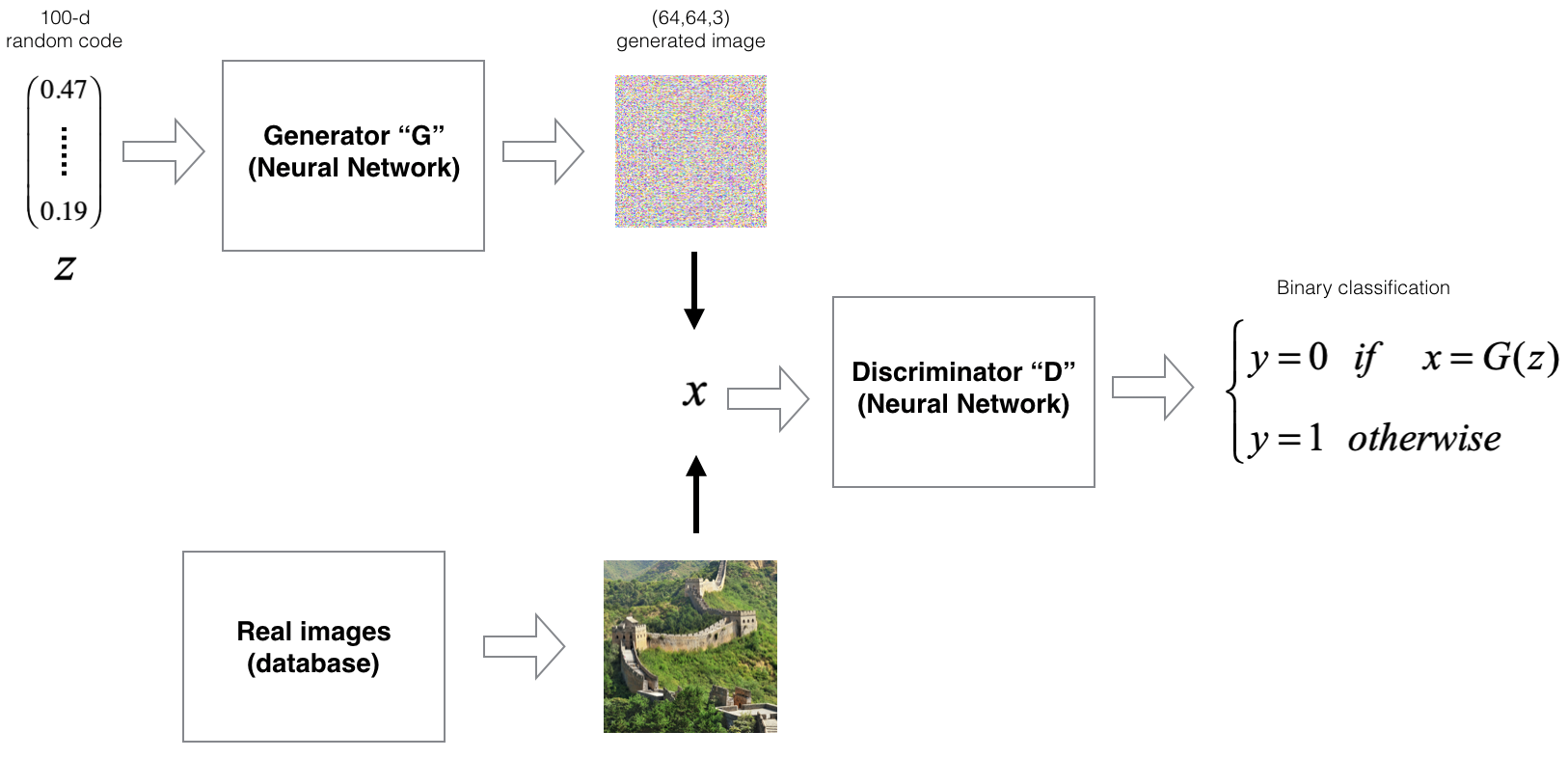
  • It is common to choose a random code \(z\) as input to \(G\), such that \(x = G(z)\) is a generated image. Later, you will learn alternative designs for z allowing you to choose the features of $$x$.

Training GANs

  • To training the GAN, you need to optimize two cost function simultaneously.

  • Discrimator cost \(J^{(D)}$:\)D\(is a binary classifier aiming to map inputs\)x=G(z)\(to\)y = 0\(and inputs\)x=x_{real}\(to\)y = 1$. Thus, the logistic loss ( binary cross-entropy loss) is appropriate:

    \[J^{(D)} = -\frac{1}{m_{\text{real}}}\sum_{i=1}^{m_{\text{real}}} y_{\text{real}}^{(i)}\log (D(x^{(i)})) -\frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} (1-y_{\text{gen}}^{(i)})\log (1-D(G(z^{(i)})))\]
    • where \(m_{\text{real}}\) (resp. \(m_{\text{gen}}$) is the number of real (resp. generated) examples in a batch.\)y_{\text{gen}}\(= 0\) and $$y_{\text{real}} = 1$.
  • Generator cost \(J^{(G)}$: Since success is measured by the ability of\)G\(to fool\)D\(,\)J^{(G)}\(should be the opposite of\)J^{(D)}$:
\[J^{(G)} = \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (1-D(G(z^{(i)})))\]

  • Note: the first term of \(J^{(D)}\) does not appear in \(J^{(G)}\) because it is independent of \(z\) and will entail no gradient during optimization.

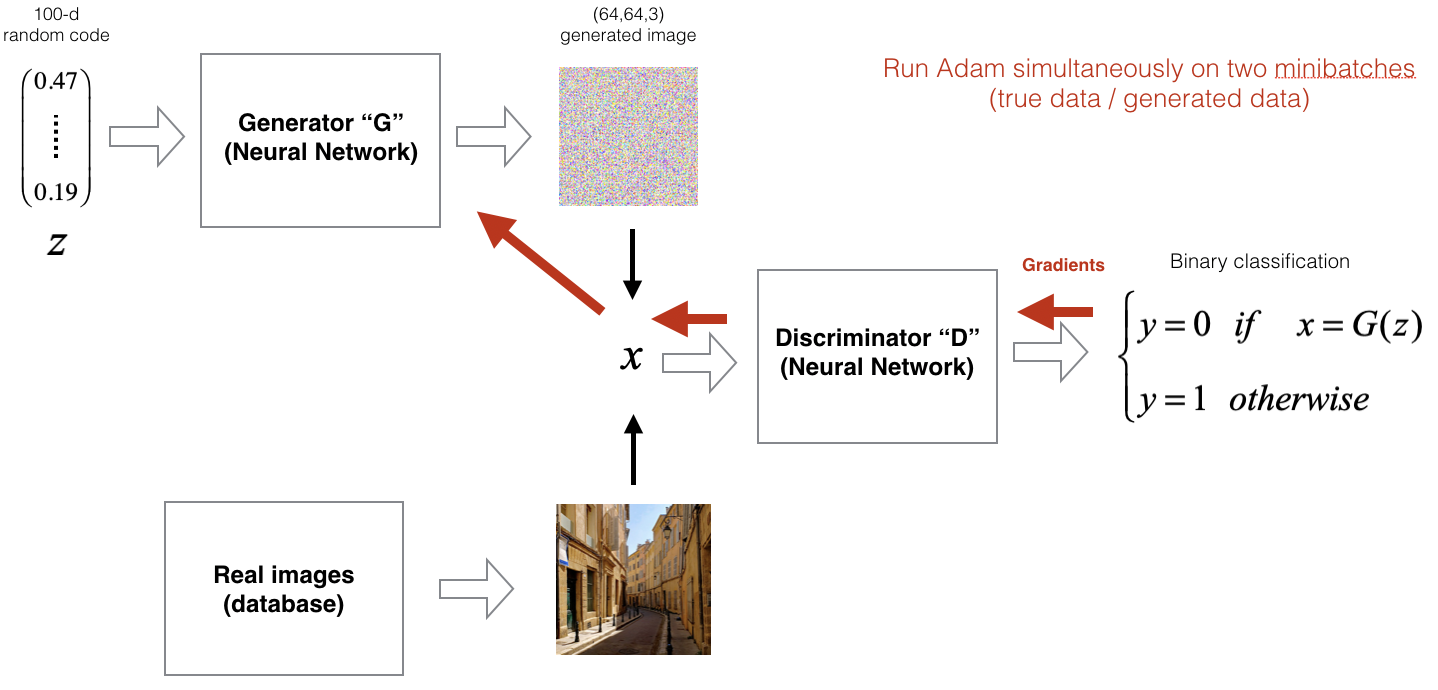
  • You can run an optimization algorithm such as Adam 3 simultaneously using two mini-batches of real and fake samples. You can think of it as a two step process:

    1. Forward propagate a mini-batch of real samples, compute \(J^{(D)}$. Then, backprogate to compute\)\frac{\partial J^{(D)}}{\partial W_D}\(where\)W_D denotes the parameters of $$D$.
    2. Forward propagate a mini-batch of samples freshly generated by \(G\), compute \(J^{(D)}\) and \(J^{(G)}$. Then backpropagate to compute\)\frac{\partial J^{(D)}}{\partial W_D}\(and\)\frac{\partial J^{(G)}}{\partial W_G}\(where\)W_G denotes the parameters of $$G$.

  • If training is successful, the distribution of fake samples coming from \(G\) should match the true distribution of data.

  • In mathematical terms, convergence is guaranteed. Here’s why:

  • This [repository]](https://github.com/eriklindernoren/Keras-GAN/blob/master/gan/gan.py) is a nice code example on how to train a GAN.

Tips to train GANs

  • In practice, training GANs is hard and requires subtle tricks.

Trick 1: Using a non-saturating cost

  • GAN training is an iterative game between \(D\) and \(G$. If\)G(z)\(isn't realistic,\)D\(doesn't need to improve. Alternatively, if\)D\(is easy to fool,\)G\(doesn't need to improve the realism of the generated samples. Consequently,\)D\(and\)G$$ need to grow together in quality.

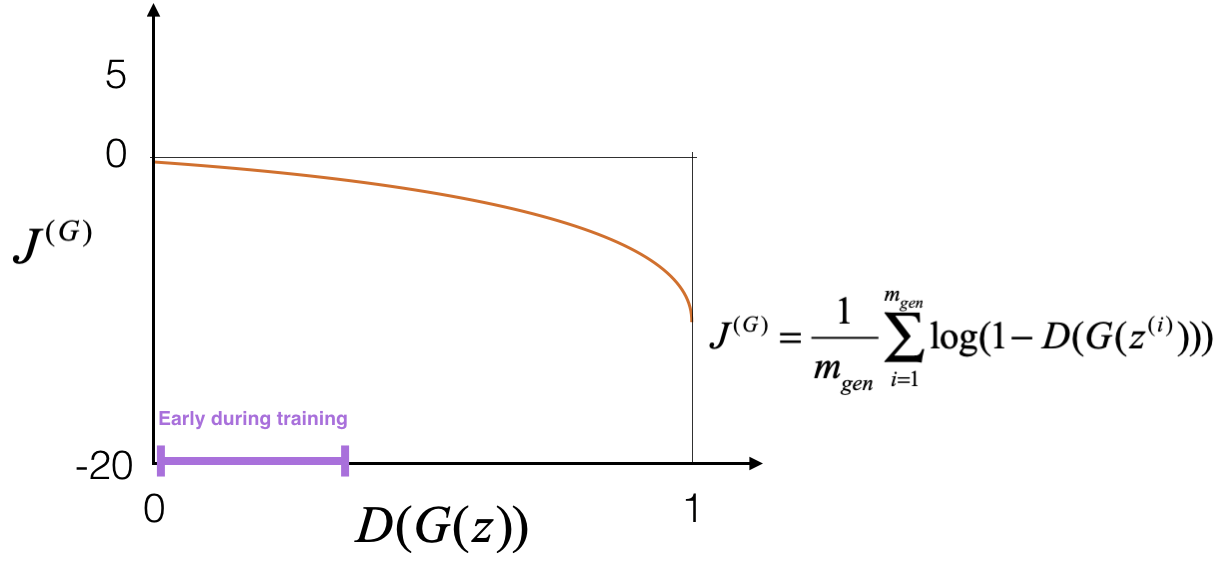
  • Early in the training, \(G\) is usually generating random noise and \(D\) easily differentiates \(x=G(z)\) from real samples. This unbalanced power hinders training. To understand why, let’s plot \(J^{(G)}\) against $$D(G(z))$:

  • On the graph above, consider the x-axis to be \(D(G(z))\) “in expectation” over a given batch of examples.

  • The gradient \(\frac{\partial J^{(G)}}{\partial D(G(z))}\) represented by the slope of the plotted function is small early in the training (i.e. when D(G(z)) is close to 0.) As a consequence, the backpropagated gradient \(\frac{\partial J^{(G)}}{\partial W_G}\) is also small. Fortunately, the following simple mathematical trick solves the problem:

\[min (J^{(G)}) = \min \Big[ \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (1-D(G(z^{(i)}))) \Big] = \max \Big[ \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (D(G(z^{(i)}))) \Big] = \min \Big[ - \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (D(G(z^{(i)}))) \Big]\]
  • As you can see on the graph below, minimizing \($ - \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (D(G(z^{(i)})))\) instead of \($ \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (1-D(G(z^{(i)})))\) ensures a higher gradient signal early in the training. Because a successful training will end when \(D(G(z)) ≈ 0.5\) (i.e. \(D\) is unable to differentiate a generated sample from a real sample), the low slope for \(D(G(z)) ≈ 1\) doesn’t slow training.

  • This approach is known as the non-saturating trick and ensures that \(G\) and \(D\) receive a stronger gradient when they are “weaker” than their counterpart.

  • You can find a more detailed explanation of the saturating cost trick in Goodfellow’s NIPS tutorial (2016).

Trick 2: Keeping D up-to-date

  • According to the non-saturating graph above, \(G\) doesn’t undergo a strong gradient when it easily fools \(D\) (i.e. in expectation \(D(G(z)) ≈ 1$.) Thus, it is strategic to ensure\)D\(is "stronger" when updating\)G$. This is achievable by updating \(D\) \(k\) times more than \(G\), with $$k>1$.
  • There exist many other tricks to successfully train GANs, this repository contains helpful supplements to our class.

Examples of GAN applications and nice results

  • GANs have been applied in myriads of applications including compressing and reconstructing images for efficient memory storage, generating super-resolution images 4 5, preserving privacy for clinical data sharing 6, generating images based on text descriptions 7, converting maps images corresponding satellite images, street scene translation 8, mass customization of medical products such as dental crowns 9, cracking enciphered language data 10 and many more. Let’s delve into some of them.

Operation on latent codes

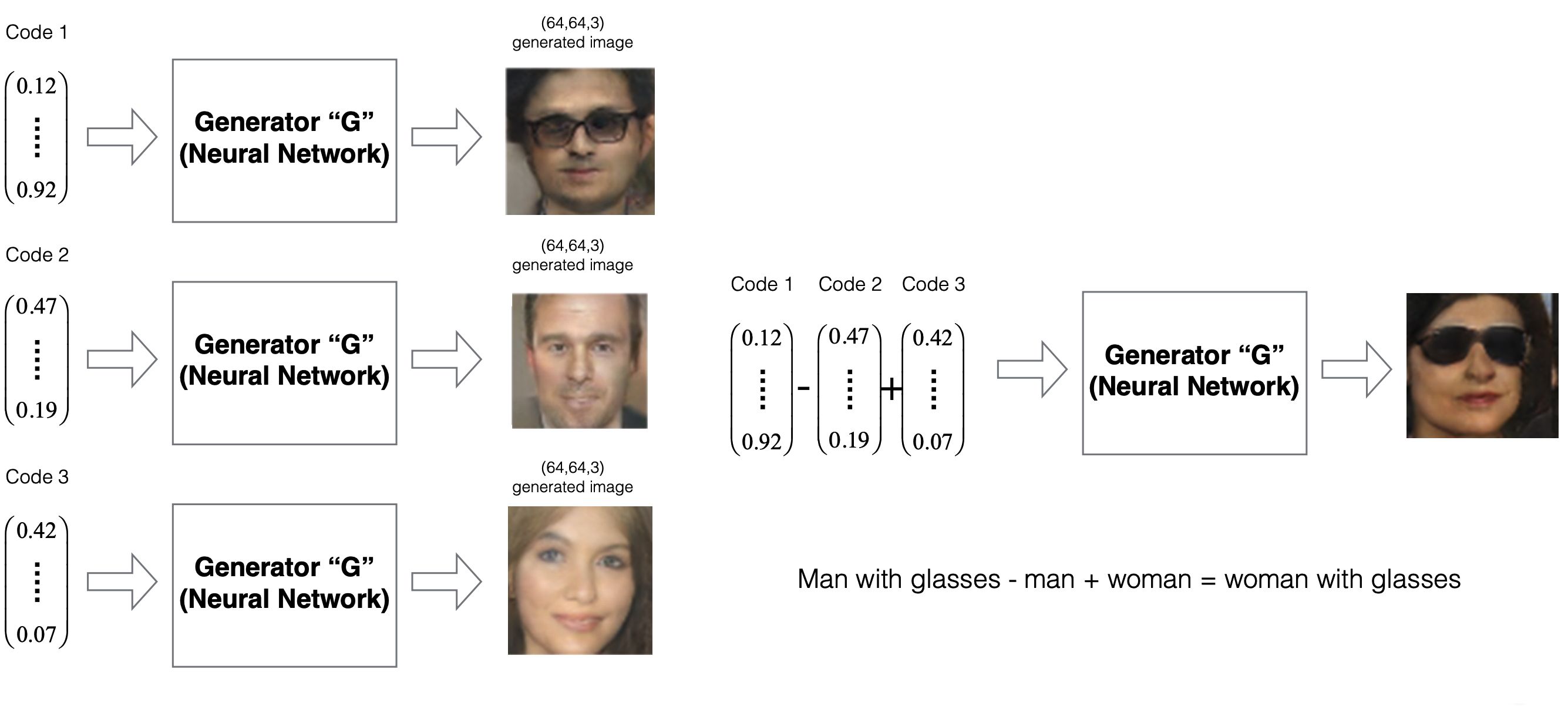
  • The latent space of random noise input, from which \(G\) maps to the real sample space, usually contains sound meanings. For instance, Radford et al. 11 show that inputing in \(G\) the latent code \(z = z_{\text{a man wearing glasses}} + z_{\text{a man without glasses}} - z_{\text{a woman without glasses}}\) leads to a generated image \(G(z)\) representing “a woman wearing glasses.”

Generating super-resolution (SR) images

  • There is promising research in GANs to recover high-resolution (HR) image from low-resolution (LR) images. Specifically, it is challenging to recover the finer texture details when super-resolving at large upscaling factors.

  • Practical applications of SR includes fast-moving vehicles identification, number plates reading 12, biomedical applications such as accurate measurement and visualization of structure in living tissues, and biometrics regnition, to name a few.

  • The following picture compares different SR algorithms’ outcome. The ground thruth is the left-most picture.

  • Here’s a picture generated by a CS230 project award winner student 13 in Fall 2018. From left to right: 32x32 LR input, SRPGGAN Output (256x256) and HR ground-truth (256x256.)

Image to Image translation via Cycle-GANs

  • Translating images between different domains has been an important application of GANs. For example, CycleGANs 14 translate horses into zebras, apples to oranges, summer features into winter features and vice-versa.

  • They consist of two pairs of generator-discriminator players: \((G_1,D_1)\) and $$(G_2,D_2)$.

  • The goal of the \((G_1, D_1)\) game is to turn domain 1 samples into domain 2 samples. In contrast, the goal of \((G_2, D_2)\) game is to turn domain 2 samples into domain 1 samples.

  • A necessary cycle constraint imposes that the composition of \(G_1\) and \(G_2\) results in the identity function, to ensure that the non-changing features (non-horse or zebra elements) are saved during the translation.

  • The training of this four-player game is summarized in five cost functions:

    • \(D_1$'s cost:\)J^{(D_1)} = -\frac{1}{m_{\text{real}}}\sum_{i=1}^{m_{\text{real}}} \log (D_1(z^{(i)})) -\frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (1-D_1(G_1(H^{(i)})))$

    • \(G_1$'s cost:\)$ J^{(G_1)} = - \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (D_1(G_1(H^{(i)})))$

    • \(D_2$'s cost:\)J^{(D_2)} = -\frac{1}{m_{\text{real}}}\sum_{i=1}^{m_{\text{real}}} \log (D_2(h^{(i)})) -\frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (1-D_2(G_2(Z^{(i)})))$

    • \(G_2$'s cost:\)$ J^{(G_2)} = - \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \log (D_2(G_2(Z^{(i)})))$

  • Cycle-consistent cost: \($ J^{\text{cycle}} = - \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \Vert G_2(G_1(H^{(i)})) - H^{(i)} \Vert_1 - \frac{1}{m_{\text{gen}}}\sum_{i=1}^{m_{\text{gen}}} \Vert G_1(G_2(Z^{(i)})) - Z^{(i)} \Vert_1\)

References

[1] Tero Karras, Samuli Laine, Timo Aila: A Style-Based Generator Architecture for Generative Adversarial Networks (2019) [2] Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio: Generative Adversarial Networks (2014) [3] Diederik P. Kingma, Jimmy Ba: Adam: A Method for Stochastic Optimization (2014) [4] Christian Ledig, Lucas Theis, Ferenc Huszar, Jose Caballero, Andrew Cunningham, Alejandro Acosta, Andrew Aitken, Alykhan Tejani, Johannes Totz, Zehan Wang, Wenzhe Shi: Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network (2016) [5] Xintao Wang, Ke Yu, Shixiang Wu, Jinjin Gu, Yihao Liu, Chao Dong, Chen Change Loy, Yu Qiao, Xiaoou Tang: ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks (2018) [6] Brett K. Beaulieu-Jones, Zhiwei Steven Wu, Chris Williams, Ran Lee, Sanjeev P. Bhavnani, James Brian Byrd, Casey S. Greene: Privacy-preserving generative deep neural networks support clinical data sharing (2017) [7] Scott Reed, Zeynep Akata, Xinchen Yan, Lajanugen Logeswaran, Bernt Schiele, Honglak Lee: Generative Adversarial Text to Image Synthesis (2016) [8] Ming-Yu Liu, Thomas Breuel, Jan Kautz: Unsupervised Image-to-Image Translation Networks (2017) [9] Jyh-Jing Hwang, Sergei Azernikov, Alexei A. Efros, Stella X. Yu: Learning Beyond Human Expertise with Generative Models for Dental Restorations (2018) [10] Aidan N. Gomez, Sicong Huang, Ivan Zhang, Bryan M. Li, Muhammad Osama, Lukasz Kaiser: Unsupervised Cipher Cracking Using Discrete GANs (2018) [11] Alec Radford, Luke Metz, Soumith Chintala: Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks (2015) [12] Yuan Jie, Du Si-dan, Zhu Xiang: Fast Super-resolution for License Plate Image Reconstruction (2008) [13] Yujie Shu: Human Portrait Super Resolution Using GANs (2018) [14] Jun-Yan Zhu, Taesung Park, Phillip Isola, Alexei A. Efros: Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks (2017)