Overview

  • This topic presents the Support Vector Machine (SVM) learning algorithm. SVMs are among the best “off-the-shelf” supervised learning algorithm.
  • To tell the SVM story, we’ll need to first talk about margins and the idea of separating data with a large “gap.” Next, we’ll talk about the optimal margin classifier, which will lead us into a digression on Lagrange duality. We’ll also see kernels, which give a way to apply SVMs efficiently in very high dimensional (such as infinite dimensional) feature spaces, and finally, we’ll close off the story with the SMO algorithm, which gives an efficient implementation of SVMs.

Margins: Intuition

  • We’ll start our story on SVMs by talking about margins. This section will give the intuitions about margins and about the “confidence” of our predictions; these ideas will be made formal in Section 3.
  • Consider logistic regression, where the probability \(P(y=1 \mid x ; \theta)\) is modeled by \(h_{\theta}(x)=g\left(\theta^{T} x\right)\). We would then predict “1” on an input \(x\) if and only if \(h_{\theta}(x) \geq 0.5\), or equivalently, if and only if \(\theta^{T} x \geq 0\).
  • Consider a positive training example \((y=1)\). The larger \(\theta^{T} x\) is, the larger also is \(h_{\theta}(x)=P(y=1 \mid x ; w, b)\), and thus also the higher our degree of “confidence” that the label is 1. Thus, informally we can think of our prediction as being a very confident one that \(y=1\) if \(\theta^{T} x \gg 0\).
  • Similarly, we think of logistic regression as making a very confident prediction of \(y=0\), if \(\theta^{T} x \ll 0\). Given a training set, again informally it seems that we’d have found a good fit to the training data if we can find \(\theta\) so that \(\theta^{T} x^{(i)} \gg 0\) whenever \(y^{(i)}=1\), and \(\theta^{T} x^{(i)} \ll 0\) whenever \(y^{(i)}=0\), since this would reflect a very confident (and correct) set of classifications for all the training examples. This seems to be a nice goal to aim, and we’ll soon formalize this idea using the notion of functional margins.
  • For a different type of intuition, consider the following figure, in which x’s represent positive training examples, o’s denote negative training examples, a decision boundary (this is the line given by the equation \(\theta^{T} x=0\), and is also called the separating hyperplane) is also shown, and three points have also been labeled \(A, B\) and \(C\).

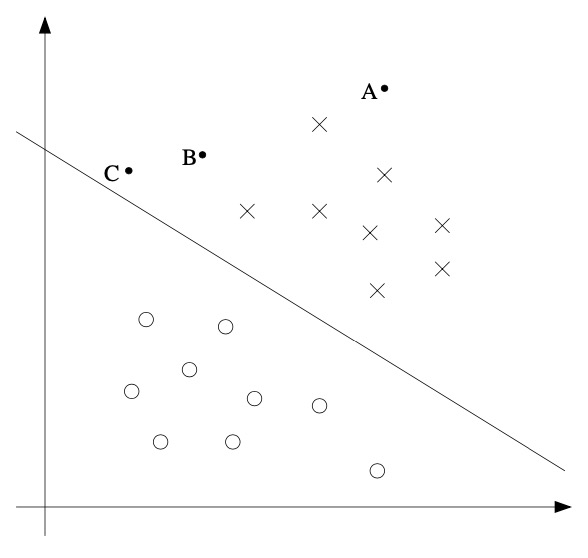
  • Notice that the point \(\mathrm{A}\) is very far from the decision boundary. If we are asked to make a prediction for the value of \(y\) at \(A\), it seems we should be quite confident that \(y=1\) there. Conversely, the point \(\mathrm{C}\) is very close to the decision boundary, and while it’s on the side of the decision boundary on which we would predict \(y=1\), it seems likely that just a small change to the decision boundary could easily have caused our prediction to be \(y=0\). Hence, we’re much more confident about our prediction at A than at C. The point \(\mathrm{B}\) lies in-between these two cases, and more broadly, we see that if a point is far from the separating hyperplane, then we may be significantly more confident in our predictions. Again, informally we think it’d be nice if, given a training set, we manage to find a decision boundary that allows us to make all correct and confident (meaning far from the decision boundary) predictions on the training examples. We’ll formalize this later using the notion of geometric margins.

Notation

  • To make our discussion of SVMs easier, we’ll first need to introduce a new notation for talking about classification. We will be considering a linear classifier for a binary classification problem with labels \(y\) and features \(x\). From now, we’ll use \(y \in\{-1,1\}\) (instead of \(\{0,1\}\)) to denote the class labels. Also, rather than parameterizing our linear classifier with the vector \(\theta\), we will use parameters \(w, b\), and write our classifier as,
\[h_{w, b}(x)=g\left(w^{T} x+b\right)\]
  • Here, \(g(z)=1\) if \(z \geq 0\), and \(g(z)=-1\) otherwise. This \(“w, b”\) notation allows us to explicitly treat the intercept term \(b\) separately from the other parameters. (We also drop the convention we had previously of letting \(x_{0}=1\) be an extra coordinate in the input feature vector.) Thus, \(b\) takes the role of what was previously \(\theta_{0}\), and \(w\) takes the role of \(\left[\theta_{1} \ldots \theta_{n}\right]^{T}\).
  • Note also that, from our definition of \(g(\cdot)\) above, our classifier will directly predict either 1 or \(-1\) (cf. the perceptron algorithm), without first going through the intermediate step of estimating the probability of \(y\) being 1 (which was what logistic regression did).

Functional and geometric margins

  • Let’s formalize the notions of the functional and geometric margins. Given a training example \(\left(x^{(i)}, y^{(i)}\right)\), we define the functional margin of \((w, b)\) with respect to the training example,
\[\hat{\gamma}^{(i)}=y^{(i)}(w^{T} x+b)\]
  • Note that if \(y^{(i)}=1\), then for the functional margin to be large (i.e., for our prediction to be confident and correct), we need \(w^{T} x+b\) to be a large positive number. Conversely, if \(y^{(i)}=-1\), then for the functional margin to be large, we need \(w^{T} x+b\) to be a large negative number. Moreover, if \(y^{(i)}\left(w^{T} x+b\right)>0\), then our prediction on this example is correct. Hence, a large functional margin represents a confident and a correct prediction.

  • For a linear classifier with the choice of \(g(\cdot)\) given above (taking values in \(\{-1,1\}\)), there’s one property of the functional margin that makes it not a very good measure of confidence, however. Given our choice of \(g(\cdot)\), we note that if we replace \(w\) with \(2 w\) and \(b\) with \(2 b\), then since \(g\left(w^{T} x+b\right)=g\left(2 w^{T} x+2 b\right)\) this would not change \(h_{w, b}(x)\) at all. i.e., \(g(\cdot)\), and hence also \(h_{w, b}(x)\), depends only on the sign, but not on the magnitude, of \(w^{T} x+b\). However, replacing \((w, b)\) with \((2 w, 2 b)\) also results in multiplying our functional margin by a factor of 2. Thus, it seems that by exploiting our freedom to scale \(w\) and \(b\) we can make the functional margin arbitrarily large without really changing anything meaningful. Intuitively, it might therefore make sense to impose some sort of normalization condition such as that \(|w|_2=1\); i.e., we might replace \((w, b)\) with \(\left(\frac{w}{|w|_2}, \frac{b}{|w|_2}\right)\), and instead consider the functional margin of \(\left(\frac{w}{|w|_2}, \frac{b}{|w|_2}\right)\). We’ll come back to this later.

  • Given a training set \(S=\left\{\left(x^{(i)}, y^{(i)}\right) ; i=1, \ldots, m\right\}\), we also define the function margin of \((w, b)\) with respect to \(S\) to be the smallest of the functional margins of the individual training examples. Denoted by \(\hat{\gamma}\), this can therefore be written:
\[\hat{\gamma}=\min _{i=1, \ldots, m} \hat{\gamma}^{(i)}\]
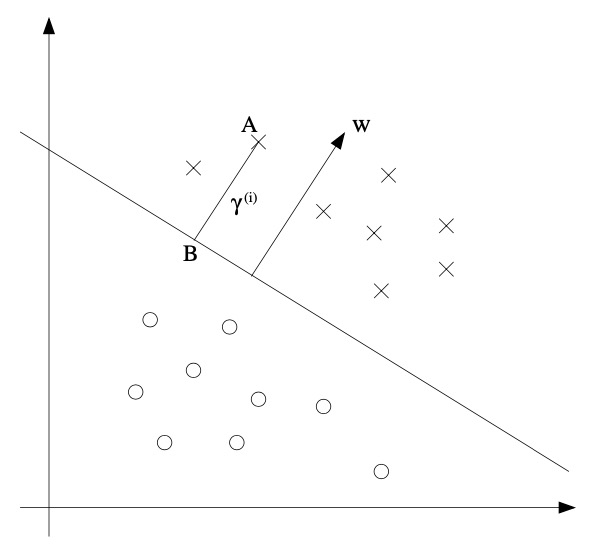
  • Next, let’s talk about geometric margins. Consider the diagram below:

  • The decision boundary corresponding to \((w, b)\) is shown, along with the vector \(w\). Note that \(w\) is orthogonal (at \(90^{\circ}\)) to the separating hyperplane. Consider the point at \(\mathrm{A}\), which represents the input \(x^{(i)}\) of some training example with label \(y^{(i)}=1\). Its distance to the decision boundary, \(\gamma^{(i)}\), is given by the line segment \(\mathrm{AB}\).

  • How can we find the value of \(\gamma^{(i)}\)? Well, \(\frac{w}{|w|}\) is a unit-length vector pointing in the same direction as \(w\). since \(A\) represents \(x^{(i)}\), we therefore find that the point \(B\) is given by \(x^{(i)}-\gamma^{(i)} \cdot \frac{w}{|w|}\). But this point lies on the decision boundary, and all points \(x\) on the decision boundary satisfy the equation \(w^{T} x+b=0\). Hence,

\[w^{T}\left(x^{(i)}-\gamma^{(i)} \frac{w}{\|w\|}\right)+b=0\]
  • Solving for \(\gamma^{(i)}\) yields,
\[\gamma^{(i)}=\frac{w^{T} x^{(i)}+b}{\|w\|}=\left(\frac{w}{\|w\|}\right)^{T} x^{(i)}+\frac{b}{\|w\|}\]
  • This was worked out for the case of a positive training example at \(\mathrm{A}\) in the figure, where being on the “positive” side of the decision boundary is good. More generally, we define the geometric margin of \((w, b)\) with respect to a training example \(\left(x^{(i)}, y^{(i)}\right)\) to be
\[\gamma^{(i)}=y^{(i)}\left(\left(\frac{w}{\|w\|}\right)^{T} x^{(i)}+\frac{b}{\|w\|}\right)\]
  • Note that if \(|w|=1\), then the functional margin equals the geometric margin-this thus gives us a way of relating these two different notions of margin. Also, the geometric margin is invariant to rescaling of the parameters; i.e., if we replace \(w\) with \(2 w\) and \(b\) with \(2 b\), then the geometric margin does not change. This will in fact come in handy later. Specifically, because of this invariance to the scaling of the parameters, when trying to fit \(w\) and \(b\) to training data, we can impose an arbitrary scaling constraint on \(w\) without changing anything important; for instance, we can demand that \(|w|=1\), or \(|w_{1}|=5\), or \(|w_{1}+b|+|w_{2}|=2\), and any of these can be satisfied simply by rescaling \(w\) and \(b\).
  • Finally, given a training set \(S=\left\{\left(x^{(i)}, y^{(i)}\right) ; i=1, \ldots, m\right\}\), we also define the geometric margin of \((w, b)\) with respect to \(S\) to be the smallest of the geometric margins on the individual training examples:
\[\gamma=\min _{i=1, \ldots, m} \gamma^{(i)}\]

The optimal margin classifier

  • Given a training set, it seems from our previous discussion that a natural desideratum is to try to find a decision boundary that maximizes the (geometric) margin, since this would reflect a very confident set of predictions on the training set and a good “fit” to the training data. Specifically, this will result in a classifier that separates the positive and the negative training examples with a “gap” (geometric margin).
  • For now, we will assume that we are given a training set that is linearly separable; i.e., that it is possible to separate the positive and negative examples using some separating hyperplane. How we we find the one that achieves the maximum geometric margin? We can pose the following optimization problem:
\[\begin{aligned} \max _{\gamma, w, b} & \gamma \\ \text { s.t. } & y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq \gamma, \quad i=1, \ldots, m \\ &\|w\|=1 \end{aligned}\]

  • i.e., we want to maximize \(\gamma\), subject to each training example having functional margin at least \(\gamma\). The \(|w|=1\) constraint moreover ensures that the functional margin equals to the geometric margin, so we are also guaranteed that all the geometric margins are at least \(\gamma\). Thus, solving this problem will result in \((w, b)\) with the largest possible geometric margin with respect to the training set.

  • If we could solve the optimization problem above, we’d be done. But the \(“\|\| w\|\|=1”\) constraint is a nasty (non-convex) one, and this problem certainly isn’t in any format that we can plug into standard optimization software to solve. So, let’s try transforming the problem into a nicer one. Consider:

\[\begin{aligned} \max _{\hat{\gamma}, w, b} & \frac{\hat{\gamma}}{\|w\|} \\ \text { s.t. } & y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq \hat{\gamma}, \quad i=1, \ldots, m \end{aligned}\]
  • Here, we’re going to maximize \(\frac{\hat{\gamma}}{\mid w \mid}\), subject to the functional margins all being at least \(\hat{\gamma}\). since the geometric and functional margins are related by \(\gamma=\frac{\hat{\gamma}}{\mid w \mid}\), this will give us the answer we want. Moreover, we’ve gotten rid of the constraint \(|w|=1\) that we didn’t like. The downside is that we now have a nasty (again, non-convex) objective \(\frac{\hat{\gamma}}{\mid w \mid}\) function; and, we still don’t have any off-the-shelf software that can solve this form of an optimization problem.
  • Recall our earlier discussion that we can add an arbitrary scaling constraint on \(w\) and \(b\) without changing anything. This is the key idea we’ll use now. We will introduce the scaling constraint that the functional margin of \(w, b\) with respect to the training set must be 1:
\[\hat{\gamma}=1\]
  • Since multiplying \(w\) and \(b\) by some constant results in the functional margin being multiplied by that same constant, this is indeed a scaling constraint, and can be satisfied by rescaling \(w, b\). Plugging this into our problem above, and noting that maximizing \(\hat{\gamma} /|w|=1 /|w|\) is the same thing as minimizing \(|w|^{2}\), we now have the following optimization problem:
\[\begin{aligned} \min _{\gamma, w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq 1, \quad i=1, \ldots, m \end{aligned}\]
  • We’ve now transformed the problem into a form that can be efficiently solved. The above is an optimization problem with a convex quadratic objective and only linear constraints. Its solution gives us the optimal margin classifier. This optimization problem can be solved using commercial quadratic programming \((\mathrm{QP})\) code.
    • You may be familiar with linear programming, which solves optimization problems that have linear objectives and linear constraints. QP software is also widely available, which allows convex quadratic objectives and linear constraints.
  • While we could call the problem solved here, what we will instead do is make a digression to talk about Lagrange duality. This will lead us to our optimization problem’s dual form, which will play a key role in allowing us to use kernels to get optimal margin classifiers to work efficiently in very high dimensional spaces. The dual form will also allow us to derive an efficient algorithm for solving the above optimization problem that will typically do much better than generic QP software.

Lagrange duality

  • Let’s temporarily put aside SVMs and maximum margin classifiers, and talk about solving constrained optimization problems. Consider a problem of the following form:
\[\begin{array}{rl} \min _{w} & f(w) \\ \text { s.t. } & h_{i}(w)=0, \quad i=1, \ldots, l \end{array}\]
  • Some of you may recall how the method of Lagrange multipliers can be used to solve it. (Don’t worry if you haven’t seen it before.) In this method, we define the Lagrangian to be
\[\mathcal{L}(w, \beta)=f(w)+\sum_{i=1}^{l} \beta_{i} h_{i}(w)\]
  • Here, the \(\beta_{i}\)’s are called the Lagrange multipliers. We would then find and set \(\mathcal{L}\)’s partial derivatives to zero:
\[\frac{\partial \mathcal{L}}{\partial w_{i}}=0 ; \quad \frac{\partial \mathcal{L}}{\partial \beta_{i}}=0\]
  • and solve for \(w\) and \(\beta\). In this section, we will generalize this to constrained optimization problems in which we may have inequality as well as equality constraints. We wouldn’t be offering a detailed treatment of the Lagrange duality right now, but we will give the main ideas and results, which we will then apply to our optimal margin classifier’s optimization problem. For more details on this topic, the curious reader can refer Convex Analysis by R. T. Rockarfeller (1970). Consider the following, which we’ll call the primal optimization problem:
\[\begin{array}{rl} \min _{w} & f(w) \\ \text { s.t. } & g_{i}(w) \leq 0, \quad i=1, \ldots, k \\ & h_{i}(w)=0, \quad i=1, \ldots, l \end{array}\]
  • To solve it, we start by defining the generalized Lagrangian
\[\mathcal{L}(w, \alpha, \beta)=f(w)+\sum_{i=1}^{k} \alpha_{i} g_{i}(w)+\sum_{i=1}^{l} \beta_{i} h_{i}(w)\]
  • Here, the \(\alpha_{i}\)’s and \(\beta_{i}\)’s are the Lagrange multipliers. Consider the quantity
\[\theta_{\mathcal{P}}(w)=\max _{\alpha, \beta: \alpha_{i} \geq 0} \mathcal{L}(w, \alpha, \beta)\]
  • Here, the “P” subscript stands for “primal.” Let some \(w\) be given. If \(w\) violates any of the primal constraints (i.e., if either \(g_{i}(w)>0\) or \(h_{i}(w) \neq 0\) for some \(i\)), then you should be able to verify that,
\[\theta_{\mathcal{P}}(w)=\max _{\alpha, \beta: \alpha_{i} \geq 0} f(w)+\sum_{i=1}^{k} \alpha_{i} g_{i}(w)+\sum_{i=1}^{l} \beta_{i} h_{i}(w) \\ \tag{1}\] \[\theta_{\mathcal{P}}(w)=\infty \tag{2}\]
  • Conversely, if the constraints are indeed satisfied for a particular value of \(w\), then \(\theta_{\mathcal{P}}(w)=f(w)\). Hence,
\[\theta_{\mathcal{P}}(w)=\left\{\begin{array}{ll} f(w) & \text { if } w \text { satisfies primal constraints } \\ \infty & \text { otherwise } \end{array}\right.\]
  • Thus, \(\theta_{\mathcal{P}}\) takes the same value as the objective in our problem for all values of \(w\) that satisfies the primal constraints, and is positive infinity if the constraints are violated. Hence, if we consider the minimization problem
\[\min _{w} \theta_{\mathcal{P}}(w)=\min _{w} \max _{\alpha, \beta: \alpha_{i} \geq 0} \mathcal{L}(w, \alpha, \beta)\]
  • we see that it is the same problem (i.e., and has the same solutions as) our original, primal problem. For later use, we also define the optimal value of the objective to be \(P^{\ast}=\min w \theta{\mathcal{P}}(w)\); we call this the value of the primal problem. Now, let’s look at a slightly different problem. We define
\[\theta_{\mathcal{D}}(\alpha, \beta)=\min _{w} \mathcal{L}(w, \alpha, \beta)\]
  • Here, the “D” subscript stands for “dual.” Note also that whereas in the definition of \(\theta_{\mathcal{P}}\) we were optimizing (maximizing) with respect to \(\alpha, \beta\), here are are minimizing with respect to \(w\). We can now pose the dual optimization problem:
\[\max _{\alpha, \beta: \alpha_{i} \geq 0} \theta_{\mathcal{D}}(\alpha, \beta)=\max _{\alpha, \beta: \alpha_{i} \geq 0} \min _{w} \mathcal{L}(w, \alpha, \beta)\]
  • This is exactly the same as our primal problem shown above, except that the order of the “max” and the “min” are now exchanged. We also define the optimal value of the dual problem’s objective to be \(d^{\ast}=\max_{\alpha, \beta: \alpha_i \geq 0} \theta_{\mathcal{D}}(w)\). How are the primal and the dual problems related? It can easily be shown that
\[d^{\ast}=\max _{\alpha, \beta: \alpha_{i} \geq 0} \min _{w} \mathcal{L}(w, \alpha, \beta) \leq \min _{w} \max _{\alpha, \beta: \alpha_{i} \geq 0} \mathcal{L}(w, \alpha, \beta)=P^{\ast}\]
  • Note that this follows from the “max min” of a function always being less than or equal to the “min max”. However, under certain conditions, we will have,
\[d^{\ast}=P^{\ast}\]
  • so that we can solve the dual problem in lieu of the primal problem. Let’s see what these conditions are.
  • Suppose \(f\) and the \(g_{i}\)’s are convex, and the \(h_{i}\)’s are affine.
    • When \(f\) has a Hessian, then it is convex if and only if the Hessian is positive semidefinite. For instance, \(f(w)=w^{T} w\) is convex; similarly, all linear (and affine) functions are also convex. (A function \(f\) can also be convex without being differentiable, but we won’t need those more general definitions of convexity here.)
    • Affine: there exists \(a_{i}, b_{i}\), so that \(h_{i}(w)=a_{i}^{T} w+b_{i}\). “Affine” means the same thing as linear, except that we also allow the extra intercept term \(b_{i}\).
  • Suppose further that the constraints \(g_{i}\) are (strictly) feasible; this means that there exists some \(w\) so that \(g_{i}(w)<0\) for all \(i\).
  • Under the above assumptions, there must exist \(w^{\ast}, \alpha^{\ast}, \beta^{\ast}\) so that \(w^{\ast}\) is the solution to the primal problem, \(\alpha^{\ast}, \beta^{\ast}\) are the solution to the dual problem, and moreover \(P^{\ast}=d^{\ast}=\mathcal{L}\left(w^{\ast}, \alpha^{\ast}, \beta^{\ast}\right)\). Moreover, \(w^{\ast}, \alpha^{\ast}\) and \(\beta^{\ast}\) satisfy the Karush-Kuhn-Tucker (KKT) conditions, which are as follows:
\[\frac{\partial}{\partial w_{i}} \mathcal{L}\left(w^{\ast}, \alpha^{\ast}, \beta^{\ast}\right) =0, \quad i=1, \ldots, n \\ \tag{3}\] \[\frac{\partial}{\partial \beta_{i}} \mathcal{L}\left(w^{\ast}, \alpha^{\ast}, \beta^{\ast}\right) =0, \quad i=1, \ldots, l \\ \tag{4}\] \[\alpha_{i}^{\ast} g_{i}\left(w^{\ast}\right) =0, \quad i=1, \ldots, k \\ \tag{5}\] \[g_{i}\left(w^{\ast}\right) \leq 0, \quad i=1, \ldots, k \\ \tag{6}\] \[\alpha^{\ast} \geq 0, \quad i=1, \ldots, k \tag{7}\]

  • Moreover, if some \(w^{\ast}, \alpha^{\ast}, \beta^{\ast}\) satisfy the KKT conditions, then it is also a solution to the primal and dual problems.

  • We draw attention to Equation \((5)\), which is called the KKT dual complementarity condition. Specifically, it implies that if \(\alpha_{i}^{\ast}>0\), then \(g_{i}\left(w^{\ast}\right)=0\). (i.e., the \(“g_{i}(w) \leq 0”\) constraint is active, meaning it holds with equality rather than with inequality.) Later on, this will be key for showing that the SVM has only a small number of “support vectors”; the KKT dual complementarity condition will also give us our convergence test when we talk about the SMO algorithm.

Optimal margin classifiers

  • Previously, we posed the following (primal) optimization problem for finding the optimal margin classifier:
\[\begin{aligned} \min _{\gamma, w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq 1, \quad i=1, \ldots, m \end{aligned}\]
  • We can write the constraints as,
\[g_{i}(w)=-y^{(i)}\left(w^{T} x^{(i)}+b\right)+1 \leq 0\]
  • We have one such constraint for each training example. Note that from the KKT dual complementarity condition, we will have \(\alpha_{i}>0\) only for the training examples that have functional margin exactly equal to one (i.e., the ones corresponding to constraints that hold with equality, \(g_{i}(w)=0\)). Consider the figure below, in which a maximum margin separating hyperplane is shown by the solid line.

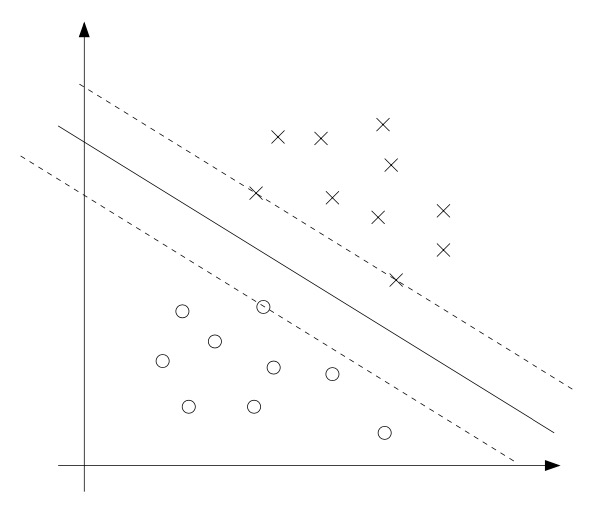
  • The points with the smallest margins are exactly the ones closest to the decision boundary; here, these are the three points (one negative and two positive examples) that lie on the dashed lines parallel to the decision boundary. Thus, only three of the \(\alpha_{i}\)’s-namely, the ones corresponding to these three training examples - will be non-zero at the optimal solution to our optimization problem. These three points are called the support vectors in this problem. The fact that the number of support vectors can be much smaller than the size the training set will be useful later.

  • Next, as we develop the dual form of the problem, one key idea to watch out for is that we’ll try to write our algorithm in terms of only the inner product \(\langle x^{(i)}, x^{(j)}\rangle\) (think of this as \((x^{(i)})^{T} x^{(j)})\) between points in the input feature space. The fact that we can express our algorithm in terms of these inner products will be key when we apply the kernel trick.

  • When we construct the Lagrangian for our optimization problem we have,
\[\mathcal{L}(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{m} \alpha_{i}\left[y^{(i)}\left(w^{T} x^{(i)}+b\right)-1\right] \tag{8}\]

  • Note that there are only “ \(\alpha_{i} “\) but no “ \(\beta_{i}\) “ Lagrange multipliers, since the problem has only inequality constraints.

  • Let’s find the dual form of the problem. To do so, we need to first minimize \(\mathcal{L}(w, b, \alpha)\) with respect to \(w\) and \(b\) (for fixed \(\alpha\)), to get \(\theta_{\mathcal{D}}\), which we’ll do by setting the derivatives of \(\mathcal{L}\) with respect to \(w\) and \(b\) to zero. We have:

\[\nabla_{w} \mathcal{L}(w, b, \alpha)=w-\sum_{i=1}^{m} \alpha_{i} y^{(i)} x^{(i)}=0\]
  • This implies that,
\[w=\sum_{i=1}^{m} \alpha_{i} y^{(i)} x^{(i)} \tag{9}\]
  • As for the derivative with respect to \(b\), we obtain,
\[\frac{\partial}{\partial b} \mathcal{L}(w, b, \alpha)=\sum_{i=1}^{m} \alpha_{i} y^{(i)}=0 \tag{10}\]
  • If we take the definition of \(w\) in Equation \((9)\) and plug that back into the Lagrangian (Equation \((8)\)), and simplify, we get,
\[\mathcal{L}(w, b, \alpha)=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{m} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left(x^{(i)}\right)^{T} x^{(j)}-b \sum_{i=1}^{m} \alpha_{i} y^{(i)}\]
  • But from Equation \((10)\), the last term must be zero, so we obtain,
\[\mathcal{L}(w, b, \alpha)=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{m} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left(x^{(i)}\right)^{T} x^{(j)}\]
  • Recall that we got to the equation above by minimizing \(\mathcal{L}\) with respect to \(w\) and \(b\). Putting this together with the constraints \(\alpha_{i} \geq 0\) (that we always had) and the constraint \((10)\), we obtain the following dual optimization problem:
\[\begin{aligned} \max _{\alpha} & W(\alpha)=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{m} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left\langle x^{(i)}, x^{(j)}\right\rangle \\ \text { s.t. } & \alpha_{i} \geq 0, \quad i=1, \ldots, m \\ & \sum_{i=1}^{m} \alpha_{i} y^{(i)}=0 \end{aligned}\]
  • You should also be able to verify that the conditions required for \(P^{\ast}=\) \(d^{\ast}\) and the KKT conditions (Equations \(\left.3-7\right)\) to hold are indeed satisfied in our optimization problem. Hence, we can solve the dual in lieu of solving the primal problem.
  • Specifically, in the dual problem above, we have a maximization problem in which the parameters are the \(\alpha_{i}\)’s. We’ll talk later about the specific algorithm that we’re going to use to solve the dual problem, but if we are indeed able to solve it (i.e., find the \(\alpha\)’s that maximize \(W(\alpha)\) subject to the constraints), then we can use Equation \((9)\) to go back and find the optimal \(w\)’s as a function of the \(\alpha\)’s. Having found \(w^{\ast}\), by considering the primal problem, it is also straightforward to find the optimal value for the intercept term \(b\) as,
\[b^{\ast}=-\frac{\max _{i: y^{(i)}=-1} w^{\ast T} x^{(i)}+\min _{i: y^{(i)}=1} w^{\ast T} x^{(i)}}{2} \tag{11}\]
  • Before moving on, let’s also take a more careful look at Equation \((9)\), which gives the optimal value of \(w\) in terms of the optimal value of \(\alpha\). Suppose we’ve fit our model’s parameters to a training set, and now wish to make a prediction at a new point input \(x\). We would then calculate \(w^{T} x+b\), and predict \(y=1\) if and only if this quantity is bigger than zero. But using \((9)\), this quantity can also be written:
\[w^{T} x+b =\left(\sum_{i=1}^{m} \alpha_{i} y^{(i)} x^{(i)}\right)^{T} x+b \\ \tag{12}\] \[=\sum_{i=1}^{m} \alpha_{i} y^{(i)}\left\langle x^{(i)}, x\right\rangle+b \tag{13}\]
  • Hence, if we’ve found the \(\alpha_{i}\)’s, in order to make a prediction, we have to calculate a quantity that depends only on the inner product between \(x\) and the points in the training set. Moreover, we saw earlier that the \(\alpha_{i}\)’s will all be zero except for the support vectors.
  • Thus, many of the terms in the sum above will be zero, and we really need to find only the inner products between \(x\) and the support vectors (of which there is often only a small number) in order calculate \((13)\) and make our prediction.
  • By examining the dual form of the optimization problem, we gained significant insight into the structure of the problem, and were also able to write the entire algorithm in terms of only inner products between input feature vectors. In the next section, we will exploit this property to apply the kernels to our classification problem. The resulting algorithm, support vector machines, will be able to efficiently learn in very high dimensional spaces.

Kernels

  • Back in our discussion of linear regression, we had a problem in which the input \(x\) was the living area of a house, and we considered performing regression using the features \(x, x^{2}\) and \(x^{3}\) (say) to obtain a cubic function.
  • To distinguish between these two sets of variables, we’ll call the “original” input value the input attributes of a problem (in this case, \(x\), the living area). When that is mapped to some new set of quantities that are then passed to the learning algorithm, we’ll call those new quantities the input features. (Unfortunately, different authors use different terms to describe these two things, but we’ll try to use this terminology consistently in these notes.)
  • We will also let \(\phi\) denote the feature mapping, which maps from the attributes to the features. For instance, in our example, we had,
\[\phi(x)=\left[\begin{array}{c} x \\ x^{2} \\ x^{3} \end{array}\right]\]
  • Rather than applying SVMs using the original input attributes \(x\), we may instead want to learn using some features \(\phi(x)\). To do so, we simply need to go over our previous algorithm, and replace \(x\) everywhere in it with \(\phi(x)\) since the algorithm can be written entirely in terms of the inner products \(\langle x, z\rangle\), this means that we would replace all those inner products with \(\langle\phi(x), \phi(z)\rangle\).
  • Specifically, given a feature mapping \(\phi\), we define the corresponding kernel to be,
\[K(x, z)=\phi(x)^{T} \phi(z)\]
  • Then, everywhere we previously had \(\langle x, z\rangle\) in our algorithm, we could simply replace it with \(K(x, z)\), and our algorithm would now be learning using the features \(\phi\).
  • Now, given \(\phi\), we could easily compute \(K(x, z)\) by finding \(\phi(x)\) and \(\phi(z)\) and taking their inner product. But what’s more interesting is that often, \(K(x, z)\) may be very inexpensive to calculate, even though \(\phi(x)\) itself may be very expensive to calculate (perhaps because it is an extremely high dimensional vector). In such settings, by using in our algorithm an efficient way to calculate \(K(x, z)\), we can get SVMs to learn in the high dimensional feature space space given by \(\phi\), but without ever having to explicitly find or represent vectors \(\phi(x)\). Let’s see an example. Suppose \(x, z \in \mathbb{R}^{n}\), and consider,
\[K(x, z)=\left(x^{T} z\right)^{2}\]
  • The above equation can also be written as,
\[\begin{aligned} K(x, z) &=\left(\sum_{i=1}^{n} x_{i} z_{i}\right)\left(\sum_{j=1}^{n} x_{i} z_{i}\right) \\ &=\sum_{i=1}^{n} \sum_{j=1}^{n} x_{i} x_{j} z_{i} z_{j} \\ &=\sum_{i, j=1}^{n}\left(x_{i} x_{j}\right)\left(z_{i} z_{j}\right) \end{aligned}\]
  • Thus, we see that \(K(x, z)=\phi(x)^{T} \phi(z)\), where the feature mapping \(\phi\) is given (shown here for the case of \(n=3\)) by,
\[\phi(x)=\left[\begin{array}{l} x_{1} x_{1} \\ x_{1} x_{2} \\ x_{1} x_{3} \\ x_{2} x_{1} \\ x_{2} x_{2} \\ x_{2} x_{3} \\ x_{3} x_{1} \\ x_{3} x_{2} \\ x_{3} x_{3} \end{array}\right]\]
  • Note that whereas calculating the high-dimensional \(\phi(x)\) requires \(O\left(n^{2}\right)\) time, finding \(K(x, z)\) takes only \(O(n)\) time -linear in the dimension of the input attributes. For a related kernel, also consider,
\[\begin{aligned} K(x, z) &=\left(x^{T} z+c\right)^{2} \\ &=\sum_{i, j=1}^{n}\left(x_{i} x_{j}\right)\left(z_{i} z_{j}\right)+\sum_{i=1}^{n}\left(\sqrt{2 c} x_{i}\right)\left(\sqrt{2 c} z_{i}\right)+c^{2} \end{aligned}\]
  • This corresponds to the feature mapping (again shown for \(n=3\)):
\[\phi(x)=\left[\begin{array}{c} x_{1} x_{1} \\ x_{1} x_{2} \\ x_{1} x_{3} \\ x_{2} x_{1} \\ x_{2} x_{2} \\ x_{2} x_{3} \\ x_{3} x_{1} \\ x_{3} x_{2} \\ x_{3} x_{3} \\ \sqrt{2 c} x_{1} \\ \sqrt{2 c} x_{2} \\ \sqrt{2 c x_{3}} \\ c \end{array}\right]\]
  • and the parameter \(c\) controls the relative weighting between the \(x_{i}\) (first order \()\) and the \(x_{i} x_{j}\) (second order) terms.
  • More broadly, the kernel \(K(x, z)=\left(x^{T} z+c\right)^{d}\) corresponds to a feature mapping to an \(\left({n+d}\right)\) feature space, corresponding of all monomials of the form \(x_{i_{1}} x_{i_{2}} \ldots x_{i_{k}}\) that are up to order \(d\). However, despite working in this \(O\left(n^{d}\right)\)-dimensional space, computing \(K(x, z)\) still takes only \(O(n)\) time, and hence we never need to explicitly represent feature vectors in this very high dimensional feature space.
  • Now, let’s talk about a slightly different view of kernels. Intuitively, (and there are things wrong with this intuition, but nevermind), if \(\phi(x)\) and \(\phi(z)\) are close together, then we might expect \(K(x, z)=\phi(x)^{T} \phi(z)\) to be large. Conversely, if \(\phi(x)\) and \(\phi(z)\) are far apart-say nearly orthogonal to each other-then \(K(x, z)=\phi(x)^{T} \phi(z)\) will be small. So, we can think of \(K(x, z)\) as some measurement of how similar are \(\phi(x)\) and \(\phi(z)\), or of how similar are \(x\) and \(z\).
  • Given this intuition, suppose that for some learning problem that you’re working on, you’ve come up with some function \(K(x, z)\) that you think might be a reasonable measure of how similar \(x\) and \(z\) are. For instance, perhaps you chose,
\[K(x, z)=\exp \left(-\frac{\|x-z\|^{2}}{2 \sigma^{2}}\right)\]
  • This is a reasonable measure of \(x\) and \(z\)’s similarity, and is close to 1 when \(x\) and \(z\) are close, and near 0 when \(x\) and \(z\) are far apart. Can we use this definition of \(K\) as the kernel in an SVM? In this particular example, the answer is yes. This kernel is called the Gaussian kernel, and corresponds to an infinite dimensional feature mapping \(\phi\). But more broadly, given some function \(K\), how can we tell if it’s a valid kernel; i.e., can we tell if there is some feature mapping \(\phi\) so that \(K(x, z)=\phi(x)^{T} \phi(z)\) for all \(x, z\)?
  • Suppose for now that \(K\) is indeed a valid kernel corresponding to some feature mapping \(\phi\). Now, consider some finite set of \(m\) points (not necessarily the training set) \(\left\{x^{(1)}, \ldots, x^{(m)}\right\}\), and let a square, \(m \times m\) matrix \(K\) be defined so that its \((i, j)\) -entry is given by \(K_{i j}=K(x^{(i)}, x^{(j)})\). This matrix is called the Kernel matrix. Note that we’ve overloaded the notation and used \(K\) to denote both the kernel function \(K(x, z)\) and the kernel matrix \(K\) due to their obvious close relationship.
  • Now, if \(K\) is a valid Kernel, then \(K_{i j}=K\left(x^{(i)}, x^{(j)}\right)=\phi\left(x^{(i)}\right)^{T} \phi\left(x^{(j)}\right)=\) \(\phi\left(x^{(j)}\right)^{T} \phi\left(x^{(i)}\right)=K\left(x^{(j)}, x^{(i)}\right)=K_{j i}\), and hence \(K\) must be symmetric. Moreover, letting \(\phi_{k}(x)\) denote the \(k\)-th coordinate of the vector \(\phi(x)\), we find that for any vector \(z\), we have,
\[\begin{aligned} z^{T} K z &=\sum_{i} \sum_{j} z_{i} K_{i j} z_{j} \\ &=\sum_{i} \sum_{j} z_{i} \phi\left(x^{(i)}\right)^{T} \phi\left(x^{(j)}\right) z_{j} \\ &=\sum_{i} \sum_{j} z_{i} \sum_{k} \phi_{k}\left(x^{(i)}\right) \phi_{k}\left(x^{(j)}\right) z_{j} \\ &=\sum_{k} \sum_{i} \sum_{j} z_{i} \phi_{k}\left(x^{(i)}\right) \phi_{k}\left(x^{(j)}\right) z_{j} \\ &=\sum_{k}\left(\sum_{i} z_{i} \phi_{k}\left(x^{(i)}\right)\right)^{2} \\ & \geq 0 \end{aligned}\]
  • The second-to-last step above used the same trick as you saw in TODO. since \(z\) was arbitrary, this shows that \(K\) is positive semi-definite \((K \geq 0)\).
  • Hence, we’ve shown that if \(K\) is a valid kernel (i.e., if it corresponds to some feature mapping \(\phi\)), then the corresponding Kernel matrix \(K \in \mathbb{R}^{m \times m}\) is symmetric positive semidefinite. More generally, this turns out to be not only a necessary, but also a sufficient, condition for \(K\) to be a valid kernel (also called a Mercer kernel). The following result is due to Mercer.
    • Many texts present Mercer’s theorem in a slightly more complicated form involving \(L^{2}\) functions, but when the input attributes take values in \(\mathbb{R}^{n}\), the version given here is equivalent.

Mercer’s theorem

  • Let \(K: \mathbb{R}^{n} \times \mathbb{R}^{n} \mapsto \mathbb{R}\) be given. Then for \(K\) to be a valid (Mercer) kernel, it is necessary and sufficient that for any \(\left\{x^{(1)}, \ldots, x^{(m)}\right\},(m<\infty)\), the corresponding kernel matrix is symmetric positive semi-definite.

  • Given a function \(K\), apart from trying to find a feature mapping \(\phi\) that corresponds to it, this theorem therefore gives another way of testing if it is a valid kernel.
  • Earlier, we also briefly talked about a couple of other examples of kernels.
    • For instance, consider the digit recognition problem, in which given an image \((16 \mathrm{x} 16\) pixels of a handwritten digit \((0-9)\), we have to figure out which digit it was. Using either a simple polynomial kernel \(K(x, z)=(x^{T} z)^{d}\) or the Gaussian kernel, SVMs were able to obtain extremely good performance on this problem. This was particularly surprising since the input attributes \(x\) were just a \(256\)-dimensional vector of the image pixel intensity values, and the system had no prior knowledge about vision, or even about which pixels are adjacent to which other ones.
    • Another example is that if the objects \(x\) that we are trying to classify are strings (say, \(x\) is a list of amino acids, which strung together form a protein), then it seems hard to construct a reasonable, “small” set of features for most learning algorithms, especially if different strings have different lengths. However, consider letting \(\phi(x)\) be a feature vector that counts the number of occurrences of each length-\(k\) substring in \(x\). If we’re considering strings of english letters, then there are \(26^{k}\) such strings. Hence, \(\phi(x)\) is a \(26^{k}\) dimensional vector; even for moderate values of \(k\), this is probably too big for us to efficiently work with (e.g., \(26^{4} \approx 460000\)). However, using (dynamic programming-ish) string matching algorithms, it is possible to efficiently compute \(K(x, z)=\phi(x)^{T} \phi(z)\), so that we can now implicitly work in this \(26^{k}\)-dimensional feature space, but without ever explicitly computing feature vectors in this space.
  • The application of kernels to support vector machines should already be clear and so we won’t dwell too much longer on it here. Keep in mind however that the idea of kernels has significantly broader applicability than SVMs. Specifically, if you have any learning algorithm that you can write in terms of only inner products \(\langle x, z\rangle\) between input attribute vectors, then by replacing this with \(K(x, z)\) where \(K\) is a kernel, you can “magically” \(“\) allow your algorithm to work efficiently in the high dimensional feature space corresponding to \(K\). For instance, this kernel trick can be applied with the perceptron to to derive a kernel perceptron algorithm. Many of the algorithms that we’ll see later in this class will also be amenable to this method, which has come to be known as the “kernel trick.”

Regularization and the non-separable case

  • The derivation of the SVM as presented so far assumed that the data is linearly separable. While mapping data to a high dimensional feature space via \(\phi\) does generally increase the likelihood that the data is separable, we can’t guarantee that it always will be so. Also, in some cases it is not clear that finding a separating hyperplane is exactly what we’d want to do, since that might be susceptible to outliers. For instance, the left figure below shows an optimal margin classifier, and when a single outlier is added in the upper-left region (right figure), it causes the decision boundary to make a dramatic swing, and the resulting classifier has a much smaller margin.

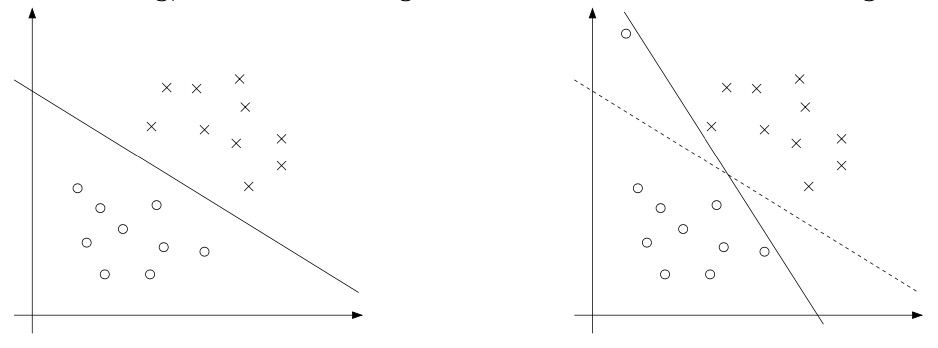
  • To make the algorithm work for non-linearly separable datasets as well as be less sensitive to outliers, we reformulate our optimization (using \(\ell_{1}\) regularization) as follows:
\[\begin{aligned} \min _{\gamma, w, b} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} \xi_{i} \\ \text { s.t. } & y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq 1-\xi_{i}, \quad i=1, \ldots, m \\ & \xi_{i} \geq 0, \quad i=1, \ldots, m \end{aligned}\]
  • Thus, examples are now permitted to have (functional) margin less than 1, and if an example has functional margin \(1-\xi_{i}(\) with \(\xi>0)\), we would pay a cost of the objective function being increased by \(C \xi_{i}\). The parameter \(C\) controls the relative weighting between the twin goals of making the \(|w|^{2}\) small (which we saw earlier makes the margin large) and of ensuring that most examples have functional margin at least 1.
  • As before, we can form the Lagrangian:
\[\mathcal{L}(w, b, \xi, \alpha, r)=\frac{1}{2} w^{T} w+C \sum_{i=1}^{m} \xi_{i}-\sum_{i=1}^{m} \alpha_{i}\left[y^{(i)}\left(x^{T} w+b\right)-1+\xi_{i}\right]-\sum_{i=1}^{m} r_{i} \xi_{i}\]
  • Here, the \(\alpha_{i}\)’s and \(r_{i}\)’s are our Lagrange multipliers (constrained to be \(\geq 0\)). We won’t go through the derivation of the dual again in detail, but after setting the derivatives with respect to \(w\) and \(b\) to zero as before, substituting them back in, and simplifying, we obtain the following dual form of the problem:
\[\begin{aligned} \max _{\alpha} & W(\alpha)=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{m} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left\langle x^{(i)}, x^{(j)}\right\rangle \\ \text { s.t. } & 0 \leq \alpha_{i} \leq C, \quad i=1, \ldots, m \\ & \sum_{i=1}^{m} \alpha_{i} y^{(i)}=0 \end{aligned}\]

  • As before, we also have that \(w\) can be expressed in terms of the \(\alpha_{i}\)’s as given in Equation \((9)\), so that after solving the dual problem, we can continue to use Equation \((13)\) to make our predictions. Note that, somewhat surprisingly, in adding \(\ell_{1}\) regularization, the only change to the dual problem is that what was originally a constraint that \(0 \leq \alpha_{i}\) has now become \(0 \leq\) \(\alpha_{i} \leq C\). The calculation for \(b^{\ast}\) also has to be modified (Equation 11 is no longer valid); see the comments in the next section/Platt’s paper.

  • Also, the KKT dual-complementarity conditions (which in the next section will be useful for testing for the convergence of the SMO algorithm) are:

\[\alpha_{i}=0 \Rightarrow y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq 1 \\ \tag{14}\] \[\alpha_{i}=C \Rightarrow y^{(i)}\left(w^{T} x^{(i)}+b\right) \leq 1 \\ \tag{15}\] \[0<\alpha_{i}<C \Rightarrow y^{(i)}\left(w^{T} x^{(i)}+b\right)=1 \tag{16}\]
  • Now, all that remains is to give an algorithm for actually solving the dual problem, which we will do in the next section.

The SMIO algorithm

  • The SMO (sequential minimal optimization) algorithm, due to John Platt, gives an efficient way of solving the dual problem arising from the derivation of the SVM. Partly to motivate the SMO algorithm, and partly because it’s interesting in its own right, let’s first take another digression to talk about the coordinate ascent algorithm.

Coordinate ascent

  • Consider trying to solve the unconstrained optimization problem
\[\max _{\alpha} W\left(\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m}\right)\]
  • Here, we think of \(W\) as just some function of the parameters \(\alpha_{i}\)’s, and for now ignore any relationship between this problem and SVMs. We’ve already seen two optimization algorithms, gradient ascent and Newton’s method. The new algorithm we’re going to consider here is called coordinate ascent: Loop until convergence: {
\[\begin{array}{l} \text { For } i=1, \ldots, m,\{ \\ \qquad \alpha_{i}:=\operatorname*{arg\,max} _{\hat{\alpha}_{i}} W\left(\alpha_{1}, \ldots, \alpha_{i-1}, \hat{\alpha}_{i}, \alpha_{i+1}, \ldots, \alpha_{m}\right) \end{array}\]
  • Thus, in the innermost loop of this algorithm, we will hold all the variables except for some \(\alpha_{i}\) fixed, and reoptimize \(W\) with respect to just the parameter \(\alpha_{i}\). In the version of this method presented here, the inner-loop reoptimizes the variables in order \(\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m}, \alpha_{1}, \alpha_{2}, \ldots\), (A more sophisticated version might choose other orderings; for instance, we may choose the next variable to update according to which one we expect to allow us to make the largest increase in \(W(\alpha) .)\)
  • When the function \(W\) happens to be of such a form that the “arg max” in the inner loop can be performed efficiently, then coordinate ascent can be a fairly efficient algorithm. Here’s a picture of coordinate ascent in action:

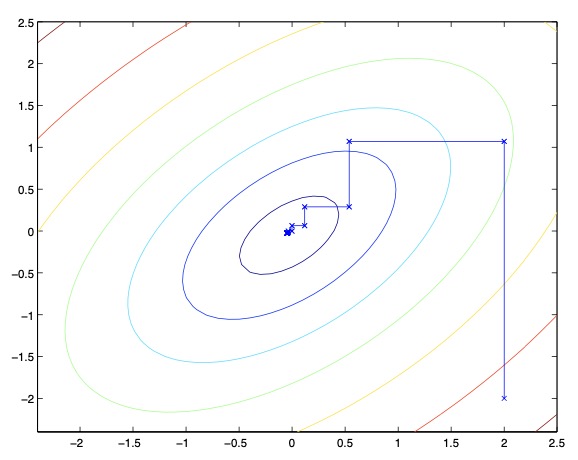
  • The ellipses in the figure are the contours of a quadratic function that we want to optimize. Coordinate ascent was initialized at \((2,-2)\), and also plotted in the figure is the path that it took on its way to the global maximum. Notice that on each step, coordinate ascent takes a step that’s parallel to one of the axes, since only one variable is being optimized at a time.

SMO

  • We close off the discussion of SVMs by sketching the derivation of the SMO algorithm. Some details will be left to the homework, and for others you may refer to the paper excerpt handed out in class. Here’s the (dual) optimization problem that we want to solve:
\[\max _{\alpha} W(\alpha)=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^m y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left\langle x^{(i)}, x^{(j)}\right\rangle \tag{17}\] \[\text { s.t. } 0 \leq \alpha_i \leq C, \quad i=1, \ldots, m \tag{18}\] \[\sum_{i=1}^{m} \alpha_{i} y^{(i)}=0 \tag{19}\]
  • Let’s say we have set of \(\alpha_{i}\)’s that satisfy the constraints \((18-19)\). Now, suppose we want to hold \(\alpha_{2}, \ldots, \alpha_{m}\) fixed, and take a coordinate ascent step and reoptimize the objective with respect to \(\alpha_{1}\). Can we make any progress? The answer is no, because the constraint (19) ensures that,
\[\alpha_{1} y^{(1)}=-\sum_{i=2}^{m} \alpha_{i} y^{(i)}\]
  • Or, by multiplying both sides by \(y^{(1)}\), we equivalently have,
\[\alpha_{1}=-y^{(1)} \sum_{i=2}^{m} \alpha_{i} y^{(i)}\]

  • This step used the fact that \(y^{(1)} \in{-1,1}\), and hence \(\left(y^{(1)}\right)^{2}=1\). Hence, \(\alpha_{1}\) is exactly determined by the other \(\alpha_{i}\)’s, and if we were to hold \(\alpha_{2}, \ldots, \alpha_{m}\) fixed, then we can’t make any change to \(\alpha_{1}\) without violating the constraint (19) in the optimization problem.

  • Thus, if we want to update some subject of the \(\alpha_{i}\)’s, we must update at least two of them simultaneously in order to keep satisfying the constraints. This motivates the SMO algorithm, which simply does the following:

    • Repeat until convergence:
      1. Select some pair \(\alpha_{i}\) and \(\alpha_{j}\) to update next. (using a heuristic that tries to pick the two that will allow us to make the biggest progress towards the global maximum).
      2. Reoptimize \(W(\alpha)\) with respect to \(\alpha_{i}\) and \(\alpha_{j}\), while holding all the other \(\alpha_{k}’s\) \((k \neq i, j)\) fixed.
  • To test for convergence of this algorithm, we can check whether the KKT conditions (Equations \(14-16\)) are satisfied to within some tol. Here, tol is the convergence tolerance parameter, and is typically set to around 0.01 to \(0.001\). (See the paper and pseudocode for details.)
  • The key reason that \(\mathrm{SMO}\) is an efficient algorithm is that the update to \(\alpha_{i}, \alpha_{j}\) can be computed very efficiently. Let’s now briefly sketch the main ideas for deriving the efficient update.
  • Let’s say we currently have some setting of the \(\alpha_{i}\)’s that satisfy the constraints \((18-19)\), and suppose we’ve decided to hold \(\alpha_{3}, \ldots, \alpha_{m}\) fixed, and want to reoptimize \(W\left(\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m}\right)\) with respect to \(\alpha_{1}\) and \(\alpha_{2}\) (subject to the constraints). From \((19)\), we require that
\[\alpha_{1} y^{(1)}+\alpha_{2} y^{(2)}=-\sum_{i=3}^{m} \alpha_{i} y^{(i)}\]
  • Since the right hand side is fixed (as we’ve fixed \(\alpha_{3}, \ldots \alpha_{m}\)), we can just let it be denoted by some constant \(\zeta\) :
\[\alpha_{1} y^{(1)}+\alpha_{2} y^{(2)}=\zeta \tag{20}\]
  • We can thus picture the constraints on \(\alpha_{1}\) and \(\alpha_{2}\) as follows:

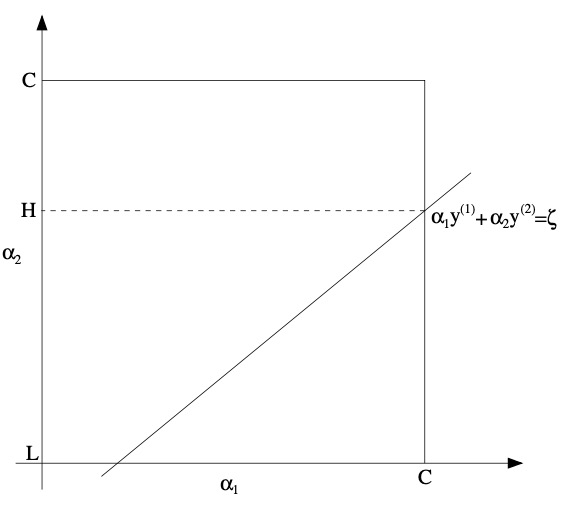
  • From the constraints \((18)\), we know that \(\alpha_{1}\) and \(\alpha_{2}\) must lie within the box \([0, C] \times[0, C]\) shown. Also plotted is the line \(\alpha_{1} y^{(1)}+\alpha_{2} y^{(2)}=\zeta\), on which we know \(\alpha_{1}\) and \(\alpha_{2}\) must lie. Note also that, from these constraints, we know \(L \leq \alpha_{2} \leq H\); otherwise, \(\left(\alpha_{1}, \alpha_{2}\right)\) can’t simultaneously satisfy both the box and the straight line constraint. In this example, \(L=0\). But depending on what the line \(\alpha_{1} y^{(1)}+\alpha_{2} y^{(2)}=\zeta\) looks like, this won’t always necessarily be the case; but more generally, there will be some lower-bound \(L\) and some upper-bound \(H\) on the permissable values for \(\alpha_{2}\) that will ensure that \(\alpha_{1}, \alpha_{2}\) lie within the box \([0, C] \times[0, C]\). Using Equation \((20)\), we can also write \(\alpha_{1}\) as a function of \(\alpha_{2}\):
\[\alpha_{1}=\left(\zeta-\alpha_{2} y^{(2)}\right) y^{(1)}\]
  • Check this derivation yourself; we again used the fact that \(y^{(1)} \in{-1,1}\) so that \(\left(y^{(1)}\right)^{2}=1\). Hence, the objective \(W(\alpha)\) can be written as,
\[W\left(\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m}\right)=W\left(\left(\zeta-\alpha_{2} y^{(2)}\right) y^{(1)}, \alpha_{2}, \ldots, \alpha_{m}\right)\]
  • Treating \(\alpha_{3}, \ldots, \alpha_{m}\) as constants, you should be able to verify that this is just some quadratic function in \(\alpha_{2}\), i.e.,, this can also be expressed in the form \(a \alpha_{2}^{2}+b \alpha_{2}+c\) for some appropriate \(a, b\), and \(c\). If we ignore the “box” constraints (18) (or, equivalently, that \(L \leq \alpha_{2} \leq H\)), then we can easily maximize this quadratic function by setting its derivative to zero and solving. We’ll let \(\alpha_{2}^{\text {new}, \text {unclipped}}\) denote the resulting value of \(\alpha_{2}\). Hypothetically, if we had instead wanted to maximize \(W\) with respect to \(\alpha_{2}\) but subject to the box constraint, then we can find the resulting value optimal simply by taking \(\alpha_{2}^{\text {new}, \text {unclipped}}\) and “clipping” it to lie in the \([L, H]\) interval, to get,
\[\alpha_{2}^{n e w}=\left\{\begin{array}{ll} H & \text { if } \alpha_{2}^{\text {new}, \text {unclipped}}>H \\ \alpha_{2}^{\text {new}, \text {unclipped}} & \text {if } L \leq \alpha_{2}^{\text {new}, \text {unclipped}} \leq H \\ L & \text { if } \alpha_{2}^{\text {new}, \text {unclipped}}<L \end{array}\right.\]

  • Finally, having found the \(\alpha_{2}^{\text {new}}\), we can use Equation \((20)\) to go back and find the optimal value of \(\alpha_{1}^{\text {new}}\).

  • There are a couple more details that are quite easy but that we’ll leave you to read about yourself in Platt’s paper: One is the choice of the heuristics used to select the next \(\alpha_{i}, \alpha_{j}\) to update; the other is how to update \(b\) as the SMO algorithm is run.

Further reading

Here are some (optional) links you may find interesting for further reading:

  • Convex Analysis by R. T. Rockarfeller (1970) for more details on the theory of Lagrange duality.

References

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledSVM,
  title   = {Support Vector Machines},
  author  = {Chadha, Aman},
  journal = {Distilled Notes for Stanford CS229: Machine Learning},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}