The \(k\)-means clustering algorithm

  • In the clustering problem, we are given a training set \(\left\{x^{(1)}, \ldots, x^{(m)}\right\}\), and want to group the data into a few cohesive “clusters.” Here, \(x^{(i)} \in \mathbb{R}^{n}\) as usual; but no labels \(y^{(i)}\) are given. So, this is an unsupervised learning problem. The \(k\)-means clustering algorithm is as follows:

    1. Initialize cluster centroids \(\mu_{1}, \mu_{2}, \ldots, \mu_{k} \in \mathbb{R}^{n}\) randomly.

    2. Repeat until convergence:

      • For every \(i\), set,
      \[c^{(i)}:=\operatorname*{arg\,min}_{j}\left\|x^{(i)}-\mu_{j}\right\|^{2}\]
      • For each \(j\), set,
      \[\mu_j:=\frac{\sum_{i=1}^{m} \mathbb{1}\{c^{(i)}=j\} x^{(i)}}{\sum_{i=1}^{m} \mathbb{1}\{c^{(i)}=j\}}\]
      • where \(\mathbb{1}\{\cdot\}\) represents the indicator function which returns 1 if its argument is true, otherwise 0. In other words, the indicator of a true statement is equal to 1 while that of a false statement is equal to 0.
  • In the algorithm above, \(k\) (a parameter of the algorithm) is the number of clusters we want to find; and the cluster centroids \(\mu_{j}\) represent our current guesses for the positions of the centers of the clusters. To initialize the cluster centroids (in step 1 of the algorithm above), we could choose \(k\) training examples randomly, and set the cluster centroids to be equal to the values of these \(k\) examples. (Other initialization methods are also possible.)
  • The inner-loop of the algorithm repeatedly carries out two steps:
    • “Assigning” each training example \(x^{(i)}\) to the closest cluster centroid \(\mu_{j}\) and,
    • Moving each cluster centroid \(\mu_{j}\) to the mean of the points assigned to it. Figure 1 shows an illustration of running \(k\)-means.
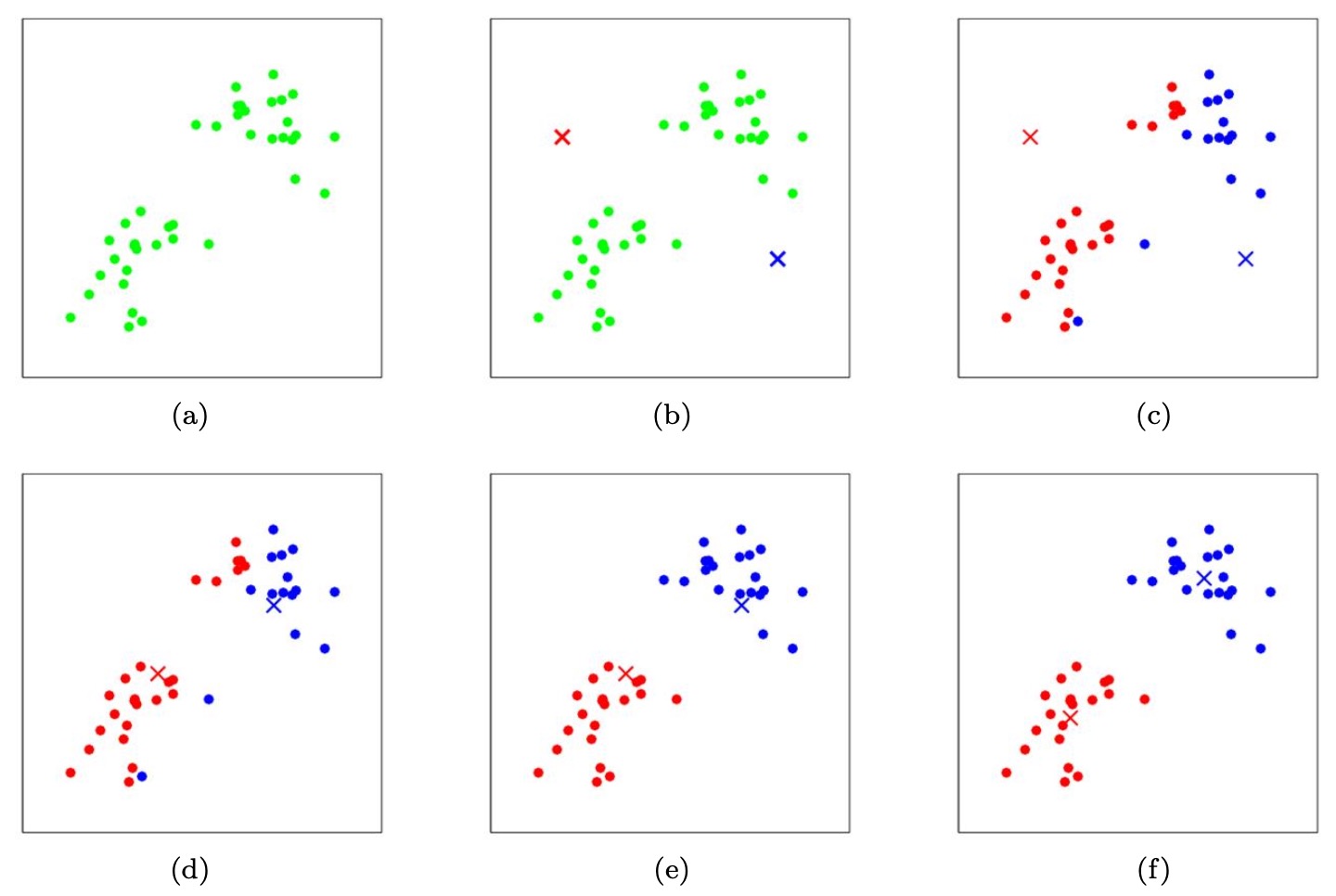
  • The figure below shows the K-means algorithm in action. Training examples are shown as dots, and cluster centroids are shown as crosses.
    • (a) Original dataset.
    • (b) Random initial cluster centroids (in this instance, not chosen to be equal to two training examples).
    • (c-f) Illustration of running two iterations of \(k\)-means. In each iteration, we assign each training example to the closest cluster centroid (shown by “painting” the training examples the same color as the cluster centroid to which is assigned); then we move each cluster centroid to the mean of the points assigned to it.
    • Images courtesy [CS281A/Stat241A: Statistical Learning Theory K-means and Expectation Maximization by Michael Jordan, UC Berkeley](http://people.eecs.berkeley.edu/~jordan/courses/281A-fall02/lectures/lecture17.pdf).

Convergence guarantee

  • Is the \(k\)-means algorithm guaranteed to converge? Yes it is, in a certain sense. In particular, let us define the distortion function to be:
\[J(c, \mu)=\sum_{i=1}^{m}\left\|x^{(i)}-\mu_{c^{(i)}}\right\|^{2}\]
  • Thus, \(J\) measures the sum of squared distances between each training example \(x^{(i)}\) and the cluster centroid \(\mu_{c^{(i)}}\) to which it has been assigned. It can be shown that \(k\)-means is exactly coordinate descent on \(J\). Specifically, the inner-loop of \(k\)-means repeatedly minimizes \(J\) with respect to \(c\) while holding \(\mu\) fixed, and then minimizes \(J\) with respect to \(\mu\) while holding \(c\) fixed. Thus, \(J\) must monotonically decrease, and the value of \(J\) must converge. Usually, this implies that \(c\) and \(\mu\) will converge too.
  • In theory, it is possible for \(k\)-means to oscillate between a few different clusterings – i.e., a few different values for \(c\) and/or \(\mu-\) that have exactly the same value of \(J\), but this almost never happens in practice).
  • The distortion function \(J(\cdot)\) is a non-convex function, and so coordinate descent on \(J\) is not guaranteed to converge to the global minimum. In other words, \(k\)-means can be susceptible to local optima. Very often \(k\)-means will work fine and come up with very good clusterings despite this.
  • If you are worried about getting stuck in bad local minima, one common thing to do is run \(k\)-means many times (using different random initial values for the cluster centroids \(\mu_{j}\)). Then, out of all the different clusterings found, pick the one that gives the lowest distortion \(J(c, \mu)\).

References

Citation

If you found our work useful, please cite it as:

@article{Chadha2020DistilledkMeansClusteringAlgorithm,
  title   = {k-Means Clustering Algorithm},
  author  = {Chadha, Aman},
  journal = {Distilled Notes for Stanford CS229: Machine Learning},
  year    = {2020},
  note    = {\url{https://aman.ai}}
}