Distilled • LeetCode • Two Pointers
- Pattern: Two Pointers
- [5/Medium] Longest Palindromic Substring
- [16/Medium] 3Sum Closest
- [16/Medium] 3Sum Closest
- [19/Medium] Remove Nth Node From End of List
- [25/Hard] Reverse Nodes in \(k\)-Group
- [42/Hard] Trapping Rain Water
- [125/Easy] Valid Palindrome
- [142/Medium] Linked List Cycle
- [142/Medium] Linked List Cycle II
- [209/Medium] Minimum Size Subarray Sum
- [408/Easy] Valid Word Abbreviation
- [647/Medium] Palindromic Substrings
- [680/Easy] Valid Palindrome II
- [986/Medium] Interval List Intersections
- [1004/Medium] Max Consecutive Ones III
- [1868/Medium] Product of Two Run-Length Encoded Arrays
Pattern: Two Pointers
- The “two pointers” pattern is of three types:
- Fast and slow (hare and tortoise): both pointers begin at the start and one (fast) travels faster (usually 2x the speed) as the other (slow).
- Meet in the middle: one pointer begins at the start (and works its way to the middle by incrementing itself) while the other begins from the end (and works its way to the middle by decrementing itself) – both meet in the middle after traversing their respective halves.
- Expand around the center (from the middle to the ends): both pointers begin at the center, work their way to the ends (by one decrementing itself and the other incrementing itself).
[5/Medium] Longest Palindromic Substring
Problem
-
Given a string
s, return the longest palindromic substring ins. -
Example 1:
Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.
- Example 2:
Input: s = "cbbd"
Output: "bb"
- Constraints:
1 <= s.length <= 1000s consist of only digits and English letters.
- See problem on LeetCode.
Solution: Two pointers (expand around the center; from the middle to the end)
class Solution:
# get the longest palindrome given l, r are the middle indexes
# from inner to outer
def largestPalindrome(self, s, l, r):
while l >= 0 and r < len(s):
if s[l] != s[r]:
break
l -= 1
r += 1
# s[l] does not match s[r] at this point;
# so we need to backtrack to the previous value of l (which is l+1)
return s[l+1:r]
def longestPalindrome(self, s: str) -> str:
maxPal = ''
for i in range(len(s)):
# even case, like "abba": self.largestPalindrome(s, i, i+1)
# odd case, like "aba": self.largestPalindrome(s, i, i)
maxPal = max(maxPal, self.largestPalindrome(s, i, i+1), self.largestPalindrome(s, i, i), key=len)
return maxPal
- The reason behind us having to treat the odd and even case differently is as follows. Let’s take the example of
iin the loop pointing to the middle character of the string:
aba: compare the middle character with itself, i.e., "i" with "i"
abba: compare the middle character with the next one, i.e., "i" with "i+1"
Complexity
- Time: \(O(n*(n + n)) = O(n^2)\)
- Space: \(O(n)\) for the slicing operation
Solution: Manacher algorithm
- Note that this algorithm is definitely non-trivial and you won’t be expected to come up with such algorithm during an interview setting.
- Based on LeetCode: Longest Palindromic Substring Part II.
class Solution:
# Manacher algorithm
# http://en.wikipedia.org/wiki/Longest_palindromic_substring
def longestPalindrome(self, s):
# Transform S into T.
# For example, S = "abba", T = "^#a#b#b#a#$".
# ^ and $ signs are sentinels appended to each end to avoid bounds checking
T = '#'.join('^{}$'.format(s))
n = len(T)
P = [0] * n
C = R = 0
for i in range (1, n-1):
P[i] = (R > i) and min(R - i, P[2*C - i]) # equals to i' = C - (i-C)
# Attempt to expand palindrome centered at i
while T[i + 1 + P[i]] == T[i - 1 - P[i]]:
P[i] += 1
# If palindrome centered at i expand past R,
# adjust center based on expanded palindrome.
if i + P[i] > R:
C, R = i, i + P[i]
# Find the maximum element in P.
maxLen, centerIndex = max((n, i) for i, n in enumerate(P))
return s[(centerIndex - maxLen)//2: (centerIndex + maxLen)//2]
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[16/Medium] 3Sum Closest
Problem
-
You are given an integer array
heightof lengthn. There are n vertical lines drawn such that the two endpoints of thei-thline are(i, 0)and(i, height[i]). -
Find two lines that together with the x-axis form a container, such that the container contains the most water.
-
Return the maximum amount of water a container can store.
-
Notice that you may not slant the container.
-
Example 1:
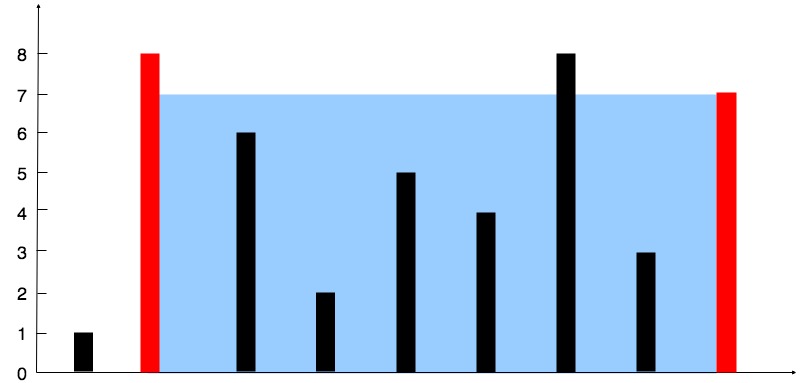
`` Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
- Example 2:
Input: height = [1,1] Output: 1
- Constraints:
- `n == height.length`
- `2 <= n <= 105`
- `0 <= height[i] <= 104`
- See [problem](https://leetcode.com/problems/container-with-most-water/) on LeetCode.
#### Solution: Two-pointers
- The first thing we should realize is that the amount of water contained is always going to be a rectangle whose area is defined as `length * width`. The width of any container will be the difference between the index of the two lines (`i` and `j`), and the height will be whichever of the two sides is the lowest (`min(H[i], H[j]`)).
- The brute force approach would be to compare every single pair of indexes in `H`, but that would be far too slow. Instead, we can observe that if we start with the lines on the opposite ends and move inward, the only possible time the area could be larger is when the height increases, since the width will continuously get smaller.
- This is very easily observed with the use of visuals. Let's say we start with a graph of `H` like this:

- The first step would be to find our starting container described by the lines on either end:

- We can tell that the line on the right end will never make a better match, because any further match would have a smaller width and the container is already the maximum height that that line can support. That means that our next move should be to slide j to the left and pick a new line:

- This is a clear improvement over the last container. We only moved over one line, but we more than doubled the height. Now, it's the line on the left end that's the limiting factor, so the next step will be to slide i to the right. Just looking at the visual, however, it's obvious that we can skip the next few lines because they're already underwater, so we should go to the first line that's larger than the current water height:

- This time, it doesn't look like we made much of a gain, despite the fact that the water level rose a bit, because we lost more in width than we made up for in height. That means that we always have to check at each new possible stop to see if the new container area is better than the current best. Just lik before we can slide j to the left again:

- This move also doesn't appear to have led to a better container. But here we can see that it's definitely possible to have to move the same side twice in a row, as the j line is still the lower of the two:

- This is obviously the last possible container to check, and like the last few before it, it doesn't appear to be the best match. Still, we can understand that it's entirely possible for the best container in a different example to be only one index apart, if both lines are extremely tall.
- Putting together everything, it's clear that we need to make a **2-pointer sliding window solution**. We'll start from either end and at each step we'll check the container area, then we'll shift the lower-valued pointer inward. Once the two pointers meet, we know that we must have exhausted all possible containers and we should return our answer (`ans`).
```python
class Solution:
def maxArea(self, height: List[int]) -> int:
retArea = 0
start = 0
end = len(height)-1
while start < end:
if height[start] <= height[end]:
retArea = max(retArea, height[start] * (end - start))
start += 1
else:
retArea = max(retArea, height[end] * (end - start))
end -= 1
return retArea
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[16/Medium] 3Sum Closest
Problem
-
Given an integer array
numsof lengthnand an integertarget, find three integers innumssuch that the sum is closest totarget. -
Return the sum of the three integers.
-
You may assume that each input would have exactly one solution.
-
Example 1:
Input: nums = [-1,2,1,-4], target = 1
Output: 2
Explanation: The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
- Example 2:
Input: nums = [0,0,0], target = 1
Output: 0
- Constraints:
3 <= nums.length <= 1000-1000 <= nums[i] <= 1000-104 <= target <= 104
- See problem on LeetCode.
Solution: Two-pointers
- Same algorithm as 3sum problem, where we sort
nums, then use two pointers to check all the possible combinations, while fixing one element. - In this problem, we just need to add a new variable
diffto track the difference between target and current best result. In addition, we move the pointers in terms of diff (be careful with the sign).
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
result, diff = sum(nums[:3]), float('inf') # or "nums[0] + nums[1] + nums[2]" instead of "sum(nums[:3])"
nums.sort()
for i in range(len(nums) - 2):
# ignore adjacent duplicates because the number at nums[i-1]
# would have already been utilized by the time we reach nums[i]
# so we just skip nums[i]
if i > 0 and nums[i] == nums[i - 1]:
continue
left, right = i + 1, len(nums) - 1
while left < right:
curSum = nums[i] + nums[left] + nums[right]
curDiff = abs(curSum - target)
if not curDiff:
return curSum
if curDiff < diff: # or if abs(curSum-target) < abs(result-target):
result = curSum
diff = curDiff
if curSum < target:
left += 1
else:
right -= 1
return result
Complexity
- Time: \(O(n^2)\)
- Space: \(O(1)\)
[19/Medium] Remove Nth Node From End of List
Problem
-
Given the
headof a linked list, remove then-thnode from the end of the list and return its head. -
Example 1:
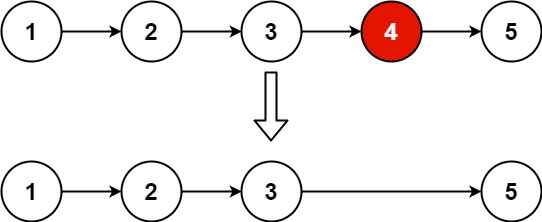
Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]
- Example 2:
Input: head = [1], n = 1
Output: []
- Example 3:
Input: head = [1,2], n = 1
Output: [1]
- Constraints:
The number of nodes in the list is sz.1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
- See problem on LeetCode.
Solution: Recursive – value-shifting
- Kind of a “cheating” solution :) Instead of really removing the
n-thnode, we remove then-thvalue. We then recursively determine the indexes (counting from back), then shift the values for all indexes larger thann, and then always drop the head.
class Solution:
def removeNthFromEnd(self, head, n):
def index(node):
if not node:
return 0
i = index(node.next) + 1
if i > n:
# shift right
node.next.val = node.val
return i
index(head)
return head.next
Solution: Recursive – Index and Remove
- Recursively determine the indexes again, but this time the helper function removes the
n-thnode. It returns two values. The index, as in the earlier solution, and the possibly changed head of the remaining list.
class Solution:
def removeNthFromEnd(self, head, n):
def remove(head):
if not head:
return 0, head
i, head.next = remove(head.next)
return i+1, (head, head.next)[i+1 == n]
return remove(head)[1]
Solution: One-pointer, two traversals
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
# Determine length of list
length = 0
node = head
while node:
node = node.next
length += 1
index_to_remove = length - n
# We can get rid of this special case but ok
if index_to_remove == 0:
return head.next
else:
node = head
curr_index = 0
while curr_index != index_to_remove - 1:
node = node.next
curr_index += 1
node.next = node.next.next
return head
Solution: Two-pointer solution – n ahead
- The standard solution, but without a dummy extra node. Instead, we simply handle the special case of removing the head right after the fast cursor gets its head start.
- With a singly linked list, the only way to find the end of the list, and thus the
n-thnode from the end, is to actually iterate all the way to the end. The challenge here is attempting to find the solution in only one pass. A naive approach here might be to store pointers to each node in an array, allowing us to calculate then-thnode from the end once we reach the end, but that would takeO(m)extra space, wheremis the length of the linked list. - A slightly less naive approach would be to only store only the last
n+1node pointers in the array. This could be achieved by overwriting the elements of the storage array in circular fashion as we iterate through the list. This would lower the space complexity toO(n+1). - However, in order to solve this problem in only one pass and
O(1)extra space, we would need to find a way to both reach the end of the list with one pointer and also reach then-thnode from the end simultaneously with a second pointer. - To do that, we can simply stagger our two pointers by
nnodes by giving the first pointer (fast) a head start before starting the second pointer (slow). Doing this will causeslowto reach then-thnode from the end at the same time thatfastreaches the end.

- Since we will need access to the node before the target node in order to remove the target node, we can use
fast.next == Noneas our exit condition, rather thanfast == None, so that we stop one node earlier. - This will unfortunately cause a problem when
nis the same as the length of the list, which would make the first node the target node, and thus make it impossible to find the node before the target node. If that’s the case, however, we can just returnhead.nextwithout needing to stitch together the two sides of the target node. - Otherwise, once we successfully find the node before the target, we can then stitch it together with the node after the target, and then return
head.
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
fast = slow = head # same as "fast, slow = head, head"
# let the fast pointer get a head start by "n" nodes
for _ in range(n):
fast = fast.next
# hit the end? this implies the node to remove is the head
# (since it "n" nodes away from the last node where we're at now)
# to handle this, cull the head node and return head.next
if not fast:
return head.next
# run the slow pointer now hand-in-hand with fast (which is "n" nodes ahead)
# use `fast.next == None` as our exit condition, rather than `fast == None`, so that we stop one node earlier.
# when fast reaches (end-1), slow would be (n-1) nodes away from the end
while fast.next:
fast, slow = fast.next, slow.next
# at this point slow would be (n-1) nodes away from the end
# so left shift node and be done
slow.next = slow.next.next
return head
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[25/Hard] Reverse Nodes in \(k\)-Group
Problem
-
Given the
headof a linked list, reverse the nodes of the listkat a time, and return the modified list. -
kis a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple ofkthen left-out nodes, in the end, should remain as it is. -
You may not alter the values in the list’s nodes, only nodes themselves may be changed.
-
Example 1:
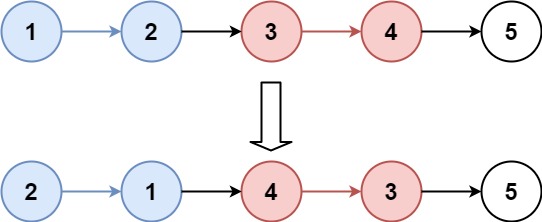
Input: head = [1,2,3,4,5], k = 2
Output: [2,1,4,3,5]
- Example 2:
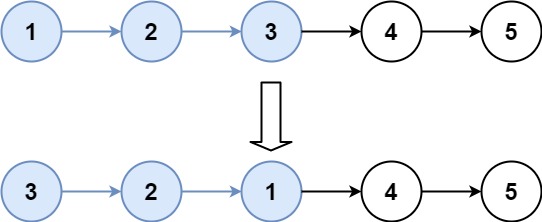
Input: head = [1,2,3,4,5], k = 3
Output: [3,2,1,4,5]
- Constraints:
The number of nodes in the list is n.1 <= k <= n <= 50000 <= Node.val <= 1000
Solution: Recursion
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
# Check if we need to reverse the group
curr = head
for _ in range(k):
if not curr:
return head
curr = curr.next
# Reverse the group (basic way to reverse linked list)
prev = None
curr = head
for _ in range(k):
nxt = curr.next
curr.next = prev
prev = curr
curr = nxt
# After reverse, we know that `head` is the tail of the group.
# And `curr` is the next pointer in original linked list order
head.next = self.reverseKGroup(curr, k)
return prev
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Two pointers
- Use a dummy head.
- Setup the following variables:
l,r: define reversing rangepre,cur: used in reversing, standard reverse linked linked list methodjump: used to connect last node in previous k-group to first node in following k-group
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
dummy = jump = ListNode(0)
dummy.next = l = r = head
while True:
count = 0
while r and count < k: # use r to locate the range
r = r.next
count += 1
if count == k: # if size k satisfied, reverse the inner linked list
pre, cur = r, l
for _ in range(k):
cur.next, cur, pre = pre, cur.next, cur # standard reversing
jump.next, jump, l = pre, l, r # connect two k-groups
else:
return dummy.next
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[42/Hard] Trapping Rain Water
Problem
-
Given
nnon-negative integers representing an elevation map where the width of each bar is1, compute how much water it can trap after raining. -
Example 1:

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
- Example 2:
Input: height = [4,2,0,3,2,5]
Output: 9
- Constraints:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
- See problem on LeetCode.
Solution: Two pointers
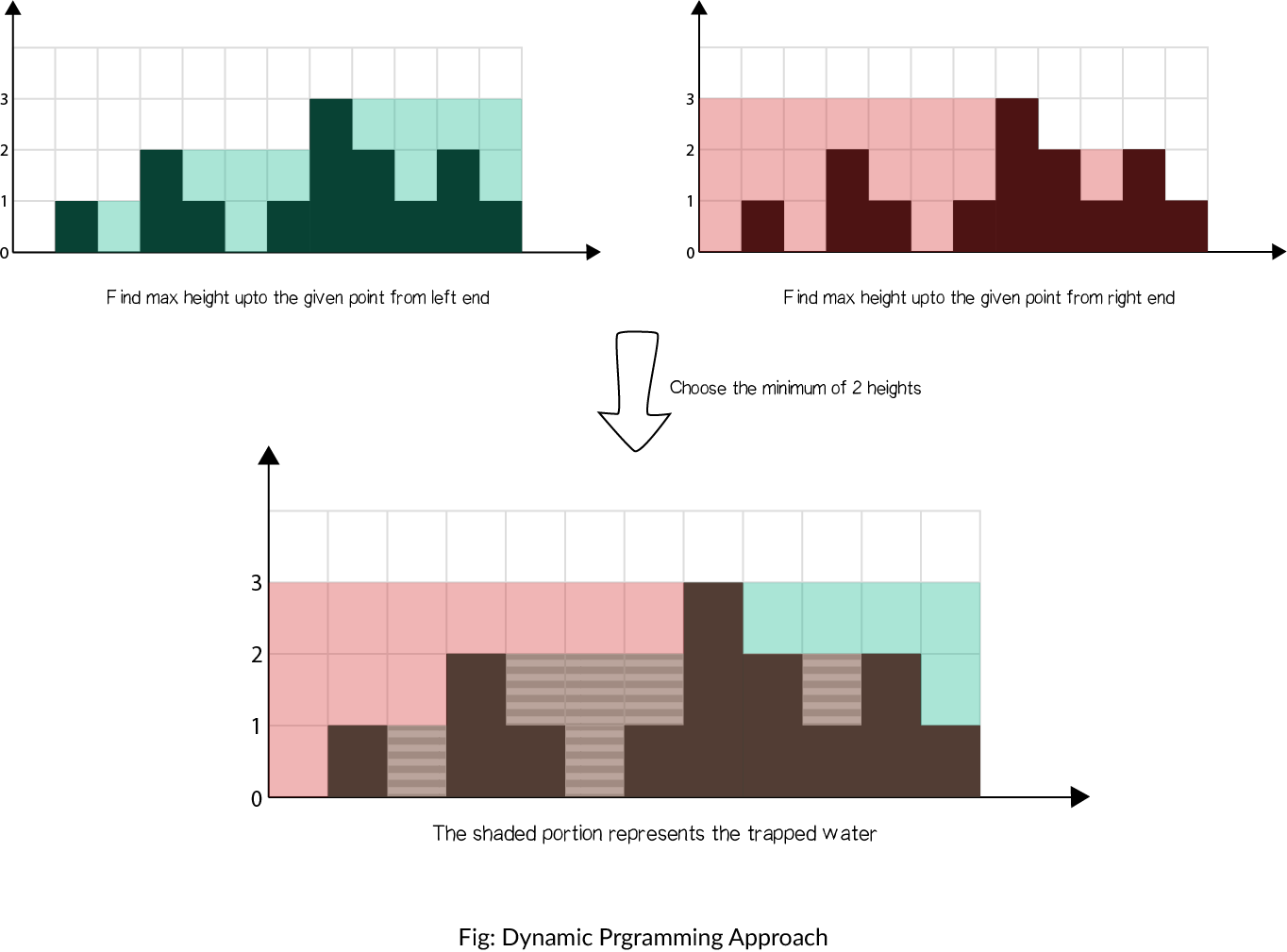
- Instead of computing the left and right parts separately, we may think of some way to do it in one iteration. From the above figure, notice that as long as
right_max[i] > left_max[i](from element 0 to 6), the water trapped depends upon theleft_max, and conversely, ifleft_max[i] > right_max[i](from element 8 to 11), the water trapped depends upon theright_max. So, we can say that if there is a larger bar at one end (say right), we are assured that the water trapped would be dependent on height of bar in current direction (from left to right). -
As soon as we find the bar at other end (right) is smaller, we start iterating in opposite direction (from right to left). We must maintain
left_maxandright_maxduring the iteration, but now we can do it in one iteration using 2 pointers, switching between the two. - Algorithm:
- Initialize
leftpointer to 0 andrightpointer tosize-1 - While
left < right, do:- If
height[left]is smaller thanheight[right]- If
height[left] >= left_max, updateleft_max - Else add
left_max - height[left]toans - Add 1 to
left.
- If
- Else:
- If
height[right] >= right_max, updateright_max - Else add
right_max - height[right]toans - Subtract 1 from
right.
- If
- If
- Initialize
- P.S.:
- For index
i, the water volume ofi:vol_i = min(left_max_i, right_max_i) - bar_i. - From left to right,
left_maxis always non-descending, whileright_maxis non-ascending.
- For index
class Solution:
def trap(self, height: List[int]) -> int:
if not height or len(height) < 3:
return 0
volume = 0
left, right = 0, len(height) - 1
l_max, r_max = height[left], height[right]
while left < right:
l_max, r_max = max(height[left], l_max), max(height[right], r_max)
if l_max <= r_max:
volume += l_max - height[left]
left += 1
else:
volume += r_max - height[right]
right -= 1
return volume
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\) since only constant space is required for
left,right,left_maxandright_max
[125/Easy] Valid Palindrome
Problem
- A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
-
Given a string
s, returntrueif it is a palindrome, or false otherwise. - Example 1:
Input: s = "A man, a plan, a canal: Panama"
Output: true
Explanation: "amanaplanacanalpanama" is a palindrome.
- Example 2:
Input: s = "race a car"
Output: false
Explanation: "raceacar" is not a palindrome.
- Example 3:
Input: s = " "
Output: true
Explanation: s is an empty string "" after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
- Constraints:
1 <= s.length <= 2 * 105s consists only of printable ASCII characters.
- See problem on LeetCode.
Solution: Two pointers (start at the ends and meet in the middle)
- Method 1:
def isPalindrome(self, s: str):
l, r = 0, len(s) - 1
while l < r:
# if the char at s[l] is not alpha-numeric
if not s[l].isalnum():
l += 1
# if the char at s[r] is not alpha-numeric
elif not s[r].isalnum():
r -= 1
# if the char at s[l] and s[r] is alpha-numeric
else:
if s[l].lower() != s[r].lower():
return False
else:
l += 1
r -= 1
return True
Complexity
- Time: \(O(n)\) since the array is looped over only once
- Space: \(O(1)\) since nothing new is created (the result is calculated in-place)
Solution: Gather all the alpha-numeric chars; check reverse
class Solution:
def isPalindrome(self, s: str):
# gather all the alpha-numeric chars
alnum_s = ''.join(e.lower() for e in s if e.isalnum())
return alnum_ == s[::-1]
#return s[:len(s)/2] == s[(len(s)+1)/2:][::-1] # This one is better, but too long
Complexity
- Time: \(O(n + n) = O(n)\) for
- Space: \(O(n + n)\) for the
alnum_ands[::-1]`
[142/Medium] Linked List Cycle
Problem
-
Given
head, the head of a linked list, determine if the linked list has a cycle in it. -
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the
nextpointer. Internally,posis used to denote the index of the node that tail’snextpointer is connected to (0-indexed). It is-1if there is no cycle. Note thatposis not passed as a parameter. -
Return
Trueif there is a cycle in the linked list. Otherwise, returnFalse. -
Example 1:
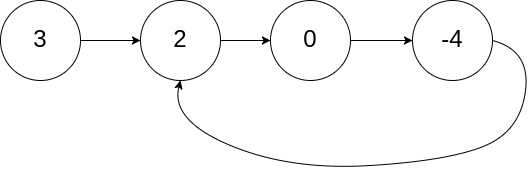
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
- Example 2:
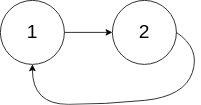
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the first node.
- Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.
- Constraints:
The number of the nodes in the list is in the range [0, 104].-105 <= Node.val <= 105pos is -1 or a valid index in the linked-list.
-
Follow up: Can you solve it using
O(1)(i.e. constant) memory? - See problem on LeetCode.
Solution: Two pointers (tortoise and hare); EAFP rather than LBYL
- The “trick” is to not check all the time whether we have reached the end but to handle it via an exception. “Easier to ask for forgiveness than permission (EAFP).”
- The next solution uses LBYL instead, i.e., use explicit extra tests checking whether next nodes actually exist before trying to access them, but this one follows EAFP. Python will check for access errors anyway, so additionally checking it myself would be a waste of time.
def hasCycle(self, head):
try:
slow = head
fast = head.next
while slow is not fast:
slow = slow.next
fast = fast.next.next
return True
except:
return False
Solution: Two pointers (tortoise and hare)
- If there is a cycle,
fastwill catchslowafter some loops.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
# @param head, a ListNode
# @return a list node
slow = fast = head
# when slow and fast meet each other, they must be on the cycle
while fast and fast.next:
# slow moves 1 step at a time, fast moves 2 steps at a time.
slow, fast = slow.next, fast.next.next
# when slow and fast meet, they are in the cycle
if slow == fast:
return True
else:
# we reach the end and there is no cycle
return False
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[142/Medium] Linked List Cycle II
Problem
-
Given the
headof a linked list, return the node where the cycle begins. If there is no cycle, returnnull. -
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the
nextpointer. Internally,posis used to denote the index of the node that tail’snextpointer is connected to (0-indexed). It is-1if there is no cycle. Note thatposis not passed as a parameter. -
Do not modify the linked list.
-
Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
- Example 2:

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.
- Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.
- Constraints:
The number of the nodes in the list is in the range [0, 104].-105 <= Node.val <= 105pos is -1 or a valid index in the linked-list.
-
Follow up: Can you solve it using
O(1)(i.e. constant) memory? - See problem on LeetCode.
Solution: Two pointers (tortoise and hare); Two parts – find if a cycle exists; determine point of entry
- The solution consists of two parts. The first one checks if a cycle exists or not. The second one determines the entry of the cycle if it exists.
- Algorithm:
Consider the following linked list, where E is the cycle entry and X, the crossing point of fast and slow. H: distance from head to cycle entry E D: distance from E to X L: cycle length _____ / \ head_____H______E \ \ / X_____/ - If slow and fast both start at head, when fast catches slow, slow has traveled H+D and fast 2(H+D). - Assume fast has traveled n loops in the cycle, we have: 2H + 2D = H + D + L --> H + D = nL --> H = nL - D - Thus if two pointers start from head and X, respectively, one first reaches E, the other also reaches E.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
# @param head, a ListNode
# @return a list node
slow = fast = head
# when slow and fast meet each other, they must be on the cycle
while fast and fast.next:
# slow moves 1 step at a time, fast moves 2 steps at a time.
slow, fast = slow.next, fast.next.next
# when slow and fast meet, they are in the cycle
if slow == fast:
break
else:
# we reach the end and there is no cycle
return None
# run head and slow until they meet
while head != slow:
head, slow = head.next, slow.next
return head
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[209/Medium] Minimum Size Subarray Sum
Problem
-
Given an array of positive integers
numsand a positive integertarget, return the minimal length of a contiguous subarray[numsl, numsl+1, ..., numsr-1, numsr]of which the sum is greater than or equal to target. If there is no such subarray, return 0 instead. -
Example 1:
Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.
- Example 2:
Input: target = 4, nums = [1,4,4]
Output: 1
- Example 3:
Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0
- Constraints:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
-
Follow up: If you have figured out the O(n) solution, try coding another solution of which the time complexity is O(n log(n)).
- See problem on LeetCode.
Solution: Two Pointers
-
Until now, we have kept the starting index of subarray fixed, and found the last position. Instead, we could move the starting index of the current subarray as soon as we know that no better could be done with this index as the starting index. We can maintain two pointers, one for the start and another for the end of the current subarray, and make optimal moves so as to keep the \(\text{sum}\) greater than \(s\) as well as maintain the lowest size possible.
-
Algorithm:
- Initialize \(\text{left}\) pointer to 0 and \(\text{sum}sum\) to 0.
- Iterate over the \(\text{nums}\):
- Add \(\text{nums}[i]\) to %%\text{sum}sum%%.
- While \(\text{sum}\) is greater than or equal to \(s\):
- Update \(\text{ans}=\min(\text{ans},i+1-\text{left})\), where \(i+1-\text{left}\) is the size of current subarray.
- It means that the first index can safely be incremented, since, the minimum subarray starting with this index with \(\text{sum} \geq s\) has been achieved.
- Subtract \(\text{nums[left]}\) from \text{sum}sum and increment \(\text{left}\).
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
left = sum = 0
res = len(nums)+1
for i in range(len(nums)):
sum += nums[i]
while sum >= target:
res = min(res, i-left+1)
sum -= nums[left]
left += 1
return res if res <= len(nums) else 0
Complexity
- Time: \(O(n). Single iteration of\)O(n)$$.
- Each element can be visited atmost twice, once by the right pointer (\(i\)) and (atmost) once by the \(\text{left}\) pointer.
- Space complexity: \(O(1)\) extra space. Only constant space required for \(\text{left}\), \(\text{sum}\), \(\text{ans}\) and \(i\).
[408/Easy] Valid Word Abbreviation
Problem
-
A string can be abbreviated by replacing any number of non-adjacent, non-empty substrings with their lengths. The lengths should not have leading zeros.
- For example, a string such as “substitution” could be abbreviated as (but not limited to):
- “s10n” (“s ubstitutio n”)
- “sub4u4” (“sub stit u tion”)
- “12” (“substitution”)
- “su3i1u2on” (“su bst i t u ti on”)
- “substitution” (no substrings replaced)
- The following are not valid abbreviations:
- “s55n” (“s ubsti tutio n”, the replaced substrings are adjacent)
- “s010n” (has leading zeros)
- “s0ubstitution” (replaces an empty substring)
- Given a string
wordand an abbreviationabbr, return whether the string matches the given abbreviation. -
A substring is a contiguous non-empty sequence of characters within a string.
- Example 1:
Input: word = "internationalization", abbr = "i12iz4n"
Output: true
Explanation: The word "internationalization" can be abbreviated as "i12iz4n" ("i nternational iz atio n").
- Example 2:
Input: word = "apple", abbr = "a2e"
Output: false
Explanation: The word "apple" cannot be abbreviated as "a2e".
- Constraints:
1 <= word.length <= 20word consists of only lowercase English letters.1 <= abbr.length <= 10abbr consists of lowercase English letters and digits.All the integers in abbr will fit in a 32-bit integer.
- See problem on LeetCode.
Solution: Two pointers
- We maintain two pointers,
ipointing atwordandjpointing atabbr. - There are only two scenarios:
jpoints to a letter. We compare the valueiandjpoints to. If equal, we increment them. Otherwise, return False.jpoints to a digit. We need to find out the complete number thatjis pointing to, e.g. 123. Then we would incrementiby 123. We know that next we will:- either break out of the while loop if i or j is too large
- or we will return to scenario 1.
class Solution(object):
def validWordAbbreviation(self, word, abbr):
"""
:type word: str
:type abbr: str
:rtype: bool
"""
i = j = 0
while j < len(abbr) and i < len(word):
if abbr[j].isalpha():
if abbr[j] != word[i]:
return False
i += 1
j += 1
else:
if abbr[j] == '0': # to handle edge cases such as "01", which are invalid
return False
temp = 0
while j < len(abbr) and abbr[j].isdigit():
temp = temp * 10 + int(abbr[j])
j += 1
i += temp
return j == len(abbr) and i == len(word)
- Same approach; rehashed:
class Solution:
def validWordAbbreviation(self, word: str, abbr: str) -> bool:
i, num = 0, 0
for j, char in enumerate(abbr):
if char.isdigit():
if num == 0 and char == '0':
return False
num = int(char) + 10*num
else:
i, num = i + num, 0
if i >= len(word) or word[i] != char:
return False
i += 1
return (i + num) == len(word)
Complexity
- Time: \(O(n)\), where \(n = max(len(word), len(abbr))\)
- Space: \(O(1)\)
[647/Medium] Palindromic Substrings
Problem
-
Given a string
s, return the number of palindromic substrings in it. -
A string is a palindrome when it reads the same backward as forward.
-
A substring is a contiguous sequence of characters within the string.
-
Example 1:
Input: s = "abc"
Output: 3
Explanation: Three palindromic strings: "a", "b", "c".
- Example 2:
Input: s = "aaa"
Output: 6
Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
- Constraints:
1 <= s.length <= 1000s consists of lowercase English letters.
- See problem on LeetCode.
Solution: Optimized mathematical solution using expand around the center approach
-
This method uses an expand around the center approach. The program iterates through each central point of a potential palindrome. moving left to right in the original input string. It then expands outward (left and right) from the center point and checks if the two characters match. This is done by moving
ato the left by one and movingbto the right by one. It keeps doing this until they don’t match (i.e.,s[a] == s[b]fails to be true) or either end of the input string is reached. This expansion of the palindrome from its center outward occurs inside of the while loop. Once the while loop exits, we have expanded as far as we could and the length of the palindrome is equal to (b - a - 1). It is useful at this point to find the pattern between the length of a palindrome and the number of palindromes it contains (with the same center). Notice the following pattern:- Palindromes of length 1 and 2 contain 1 palindrome:
aandaaeach contain one palindrome with the same center: a contains itself andaacontains itself
- Palindromes of length 3 and 4 contain 2 palindromes:
abaandabbaeach contain two palindromes with the same center:abacontainsband itself andabbacontainsbband itself
- Palindromes of length 5 and 6 contain 3 palindromes:
abcbaandabccbaeach contain three palindromes with the same center:abcbacontainsc,bcb, and itself andabccbacontainscc,bccb, and itself
- etc. …
- Palindromes of length 1 and 2 contain 1 palindrome:
- The reason we are only counting palindromes with the same center and not other palindromes it may contain is because we will have already counted them earlier in the for loop or will encounter them later in the for loop. It is important that we do not double count. Reflecting at the pattern above we can easily see that a palindrome of length L will contain
(L+1)//2palindromes within it that have the same center. Since the length of our palindrome is (b - a - 1), it follows that the number of palindromes within it will be(b - a)//2. Thus at the end of the while loop, we add(b-a)//2torwhich is counting the total number of palindromes found thus far. - Perhaps the most important (and most challenging) part of the program occurs in the structure of the inner for loop: for
a,bin[(i,i),(i,i+1)]This part may take a little explanation to fully understand. A palindrome can be centered in one of two places. The palindrome dad is centered on one of its letters, specifically the lettera. If you had to pick two indices to describe where the palindrome dad is centered you would say that it was centered at the indices 1 and 1, since 1 is the index ofa. In general such palindromes (palindromes with an odd number of elements) are centered at(i,i)for some indexi. The other type of palindrome,abbais centered in between two identical letters, specifically it is centered between the lettersbandb. If you had to pick two indices to describe where the palindromeabbais centered you would say that it was centered at the indices 1 and 2, since 1 and 2 are the indices of the central twob’s. In general such palindromes (palindromes with an even number of elements) are centered at(i,i+1)for some indexi. To correctly look at all the palindrome substrings, for each indexiin the for loop we have to consider both central pivoting points. This is why the inner for loop iterates through both(i,i)and(i,i+1). - The program ends by returning
r, the final total count of palindromes found within the original strings. - Glossary of Variables:
L= length of original input stringr= total current count of palindromic substringsa= number of units left of center of palindromeb= number of units right of center of palindrome
class Solution:
def countSubstrings(self, s: str) -> int:
L, r = len(s), 0
for i in range(L):
for a,b in [(i,i),(i,i+1)]:
while a >= 0 and b < L and s[a] == s[b]:
a -= 1; b += 1
r += (b-a)//2
return r
Solution: DP
- Start from the smallest palindrome.
- It is either:
- a single character, which is a palindrome by definition
- example: “a”
- two characters that are the same
- example: “aa”
- a single character, which is a palindrome by definition
- To determine if bigger substring is a palindrome you should know
- if the inner substring is the palindrome and
- if the outer characters match
- Refer this video for a visual intro.
class Solution(object):
def countSubstrings(self, s: str) -> int:
"""
:type s: str
:rtype: int
"""
n = len(s)
res = 0
# create a matrix to store info about the substring
dp = [[0 for i in range(n)] for j in range(n)]
# set single characters as palindromes
idx = 0
while idx < n:
dp[idx][idx] = 1
idx += 1
res += 1
# fill the matrix
# example1: "aaaaa"
# [1, 1, 1, 1, 1]
# [0, 1, 1, 1, 1]
# [0, 0, 1, 1, 1]
# [0, 0, 0, 1, 1]
# [0, 0, 0, 0, 1]
# example2: "cdaabaad"
# [1, 0, 0, 0, 0, 0, 0, 0]
# [0, 1, 0, 0, 0, 0, 0, 1]
# [0, 0, 1, 1, 0, 0, 1, 0]
# [0, 0, 0, 1, 0, 1, 0, 0]
# [0, 0, 0, 0, 1, 0, 0, 0]
# [0, 0, 0, 0, 0, 1, 1, 0]
# [0, 0, 0, 0, 0, 0, 1, 0]
# [0, 0, 0, 0, 0, 0, 0, 1]
for col in range(1, len(s)):
for row in range(col):
# every two chars are palindromes as well
if row == col - 1 and s[col] == s[row]:
dp[row][col] = 1
res += 1
# to determine if substring is a palindrome you should know
# a) if the inner substring is the palindrome and
# b) if the outer characters match
elif dp[row + 1][col - 1] == 1 and s[col] == s[row]:
dp[row][col] = 1
res += 1
# print matrix
# for line in dp:
# print(line)
return res
Solution: Two pointers (expand around center) + Recursion
- Similar solution as in the longest palindromic substring problem. Count the number of palindromes starting from the ‘center’ of a string.
class Solution:
def countSubstrings(self, s: str) -> int:
def expand(left: int, right: int) -> int:
count = 0
while left >= 0 and right < len(s) and s[left] == s[right]:
# count the palindrome and expand outward
count += 1
left -= 1
right += 1
return count
palindromes = 0
for i in range(len(s)):
# the idea is to expand around the 'center' of the string, but the center could be 1 or 2 letters
# e.g., babab and cbbd, hence the (i, i) and (i, i + 1)
palindromes += expand(i, i)
palindromes += expand(i, i+ 1)
return palindromes
Complexity
- Time: \(O(n^2)\)
- Space: \(O(1)\)
[680/Easy] Valid Palindrome II
Problem
-
Given a string
s, return true if thescan be palindrome after deleting at most one character from it. -
Example 1:
Input: s = "aba"
Output: true
- Example 2:
Input: s = "abca"
Output: true
Explanation: You could delete the character 'c'.
- Example 3:
Input: s = "abc"
Output: false
- Constraints:
1 <= s.length <= 105s consists of lowercase English letters.
- See problem on LeetCode.
Solution: Two pointers + Recursion
- Simply checking if character at
leftmatches correspondingrightuntil it doesn’t. - At that point we have a choice of either deleting the
leftorrightcharacter. If either returns palindrome, we returnTrue. - To generalize this to more than one deletes, we can simply replace the flag
deletedto be a counter initialized to how many characters we are allowed to delete and stop allowing for recursive calls when it reaches 0. - Note that this solution is generalizable to
ndeletes:
class Solution(object):
def validPalindrome(self, s: str) -> bool:
def verify(s, left, right, deleted):
while left < right:
if s[left] != s[right]:
if deleted:
return False
else:
return verify(s, left+1, right, True) or verify(s, left, right-1, True)
else:
left += 1
right -= 1
return True
return verify(s, 0, len(s)-1, False)
- Modified for
ndeletes:
class Solution(object):
def validPalindrome(self, s: str) -> bool:
def verify(s, left, right, counter=0):
while left < right:
if s[left] != s[right]:
if counter == 1:
return False
else:
return verify(s, left+1, right, counter+1) or verify(s, left, right-1, counter+1)
else:
left += 1
right -= 1
return True
return verify(s, 0, len(s)-1)
Complexity
- Time: \(O(n^2)\)
- Space: \(O(1)\)
Solution: Two pointers (meet in the middle)
class Solution:
def validPalindrome(self, s: str) -> bool:
p1 = 0 # start
p2 = len(s) - 1 # end
# meet in the middle
while p1 <= p2:
# if we break the palindromic
if s[p1] != s[p2]:
# skip the character at index p1 for string1
string1 = s[:p1] + s[p1+1:]
# skip the character at index p2 for string2
string2 = s[:p2] + s[p2+1:]
# if either reversed string matches it's original version, we're good!
return string1 == string1[::-1] or string2 == string2[::-1]
# move pointer p1 to the right
p1 += 1
# move pointer p2 to the left
p2 -= 1
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[986/Medium] Interval List Intersections
Problem
-
You are given two lists of closed intervals,
firstListandsecondList, wherefirstList[i] = [start_i, end_i]andsecondList[j] = [start_j, end_j]. Each list of intervals is pairwise disjoint and in sorted order. -
Return the intersection of these two interval lists.
-
A closed interval
[a, b](witha <= b) denotes the set of real numbersxwitha <= x <= b. -
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of
[1, 3]and[2, 4]is[2, 3]. -
Example 1:
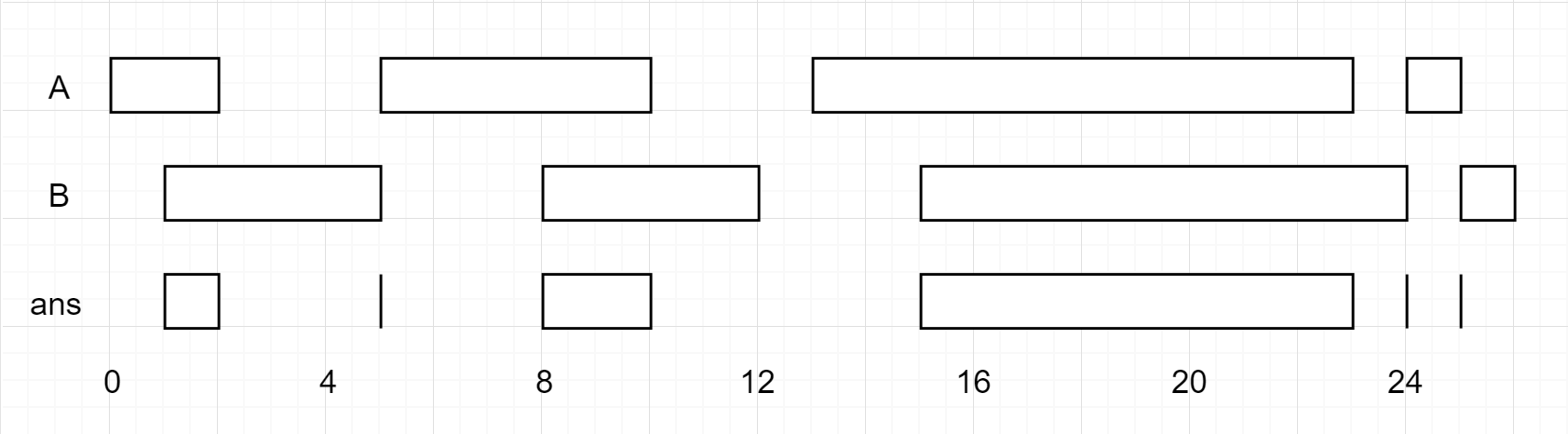
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
- Example 2:
Input: firstList = [[1,3],[5,9]], secondList = []
Output: []
- Constraints:
0 <= firstList.length, secondList.length <= 1000firstList.length + secondList.length >= 10 <= start_i < end_i <= 109end_i < start_i+10 <= start_j < end_j <= 109end_j < start_j+1
- See problem on LeetCode.
Solution: Combine and sort, check overlap and add smaller end to result
- Analysis:
- Combine and sort the two lists. Yes, this isn’t as efficient as walking through the two lists once with two pointers, but at least you don’t have to worry about tracking and advancing two pointers.
- Then, iterate through the combined list. Each iteration, if the start of the interval is less than or equal to the highest end (
currentEnd) we have encountered, add that interval to the intersection list. Then, check if the end of the interval is higher than the previous highest (currentEnd).
def intervalIntersection(self, A: List[List[int]], B: List[List[int]]) -> List[List[int]]:
combined = sorted(A + B, key=itemgetter(0))
intersection = []
currentEnd = -1
for start, end in combined:
if start <= currentEnd:
intersection.append([start, min(currentEnd, end)])
currentEnd = max(currentEnd, end)
return intersection
Complexity
- Time: \(O((m+n)*log(m+n))\)
- Space: \(O(m+n)\) for both
combinedandintersection
Solution: Two pointers
- Intuition:
- In an interval
[a, b], callbthe “endpoint”. - Among the given intervals, consider the interval
A[0]with the smallest endpoint. (Without loss of generality, this interval occurs in arrayA.) - Then, among the intervals in array
B,A[0]can only intersect one such interval in arrayB. (If two intervals inBintersectA[0], then they both share the endpoint ofA[0]– but intervals inBare disjoint, which is a contradiction.)
- In an interval
- Algorithm:
- If
A[0]has the smallest endpoint, it can only intersectB[0]. After, we can discardA[0]since it cannot intersect anything else. - Similarly, if
B[0]has the smallest endpoint, it can only intersectA[0], and we can discardB[0]after since it cannot intersect anything else. - We use two pointers,
iandj, to virtually manage “discarding”A[0]orB[0]repeatedly.
- If
- First part - Finding overlapping range:
- Let’s see the possible types of overlaps:
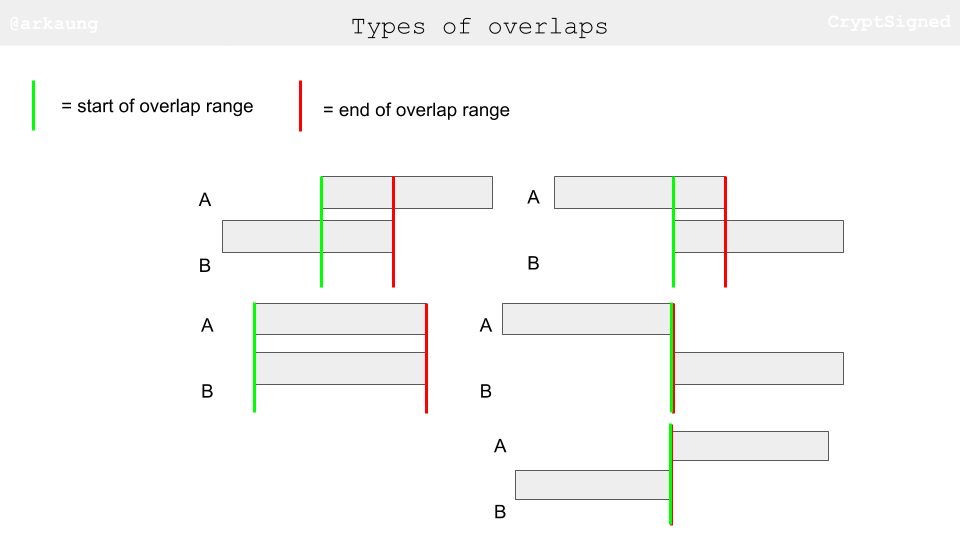
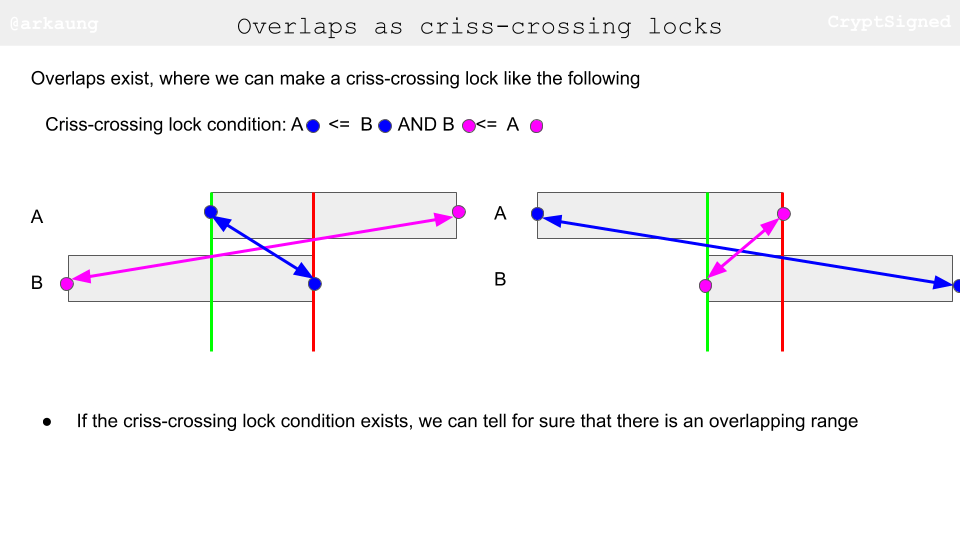
- What’s the condition for two ranges to have an overlapping range? Check out the figures below. If we can have a criss-crossing lock condition satisfied, we have essentially found an overlapping range.
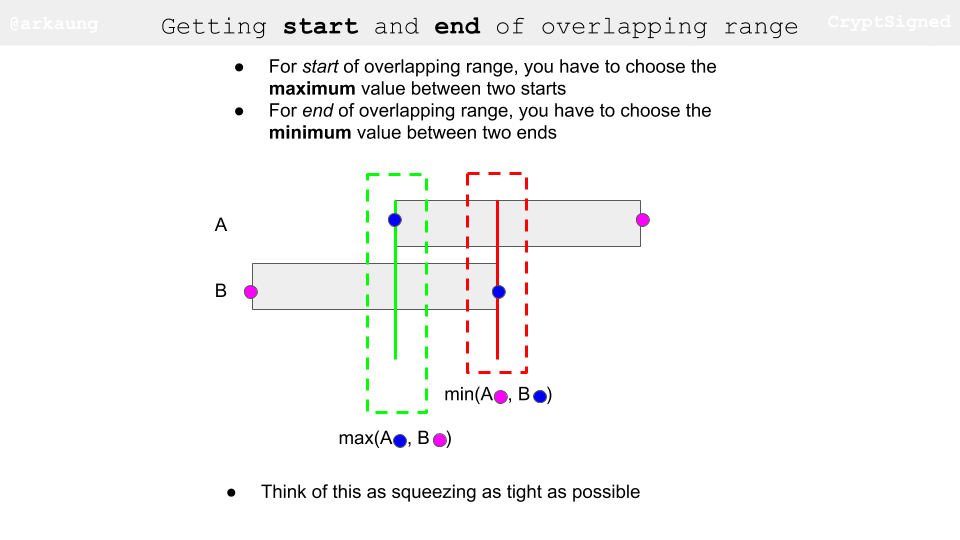
- After we have made sure that there is an overlapping range, we need to figure out the start and end of the overlapping range. Think of this as trying to squeeze the overlapping range as tight as possible (pushing as far right as possible for start and pushing as far left as possible for end).
- Second part - Incrementing pointers:
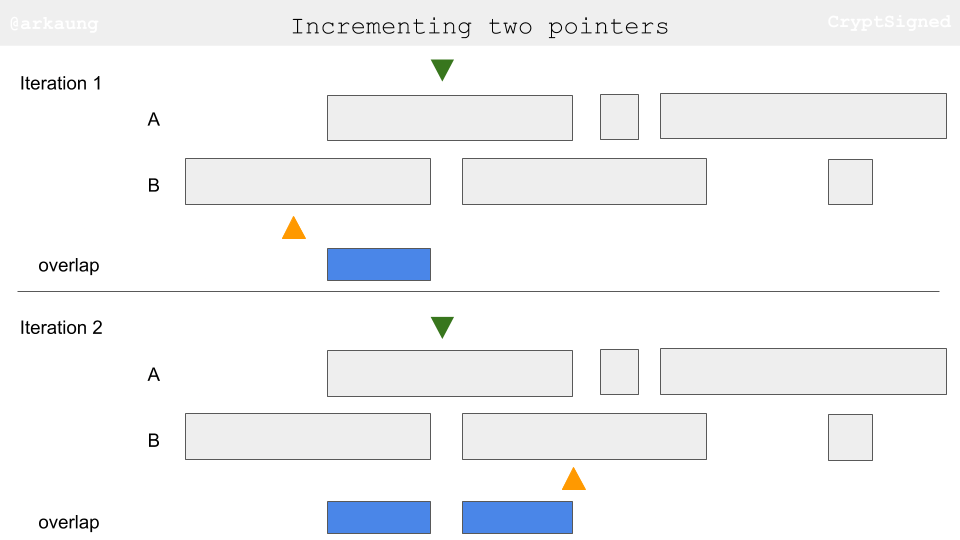
- The idea behind is to increment the pointer based on the end values of two ranges. Let’s say the current range in
Ahas end value smaller than to equal to end value of the current range inB, that essentially means that you have exhausted that range inAand you should move on to the next range. Let’s try to visually think about this. When you are going through the images, keep track of end values of the ranges and how the little pointer triangles progress.
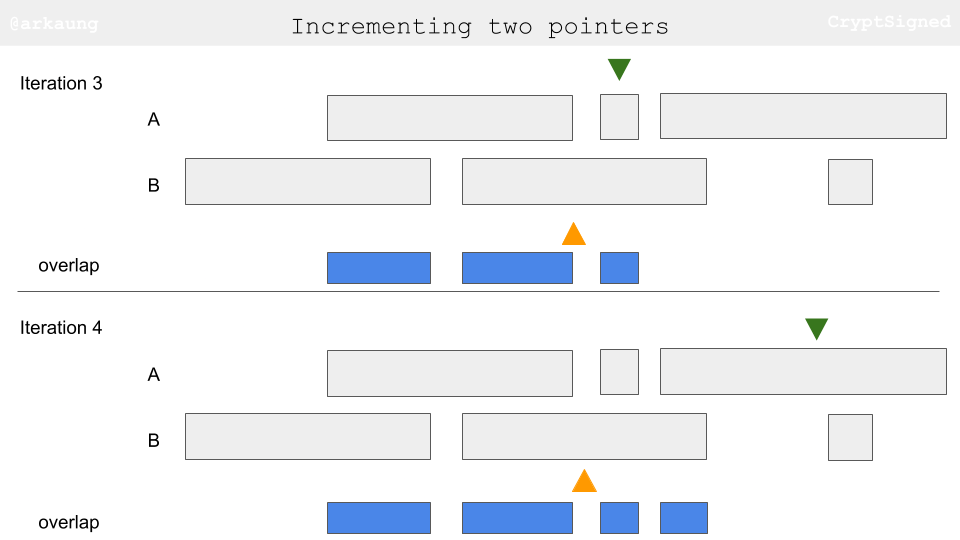

- The idea behind is to increment the pointer based on the end values of two ranges. Let’s say the current range in
class Solution:
def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
ans = []
i = j = 0
while i < len(firstList) and j < len(secondList):
# Let's check if A[i] intersects B[j].
# lo - the startpoint of the intersection
# hi - the endpoint of the intersection
lo = max(firstList[i][0], secondList[j][0])
hi = min(firstList[i][1], secondList[j][1])
if lo <= hi: # Criss-cross lock
ans.append([lo, hi]) # Squeezing
# Remove the interval with the smallest endpoint
if firstList[i][1] < secondList[j][1]: # Exhausted this range in A
i += 1 # Point to next range in A
else: # Exhausted this range in B
j += 1 # Point to next range in B
return ans
Complexity
- Time: \(O(m + n)\), where \(m\), \(n\) are the lengths of \(A\) and \(B\) respectively.
- Space: \(O(m + n)\), the maximum size of the answer.
[1004/Medium] Max Consecutive Ones III
Problem
-
Given a binary array
numsand an integerk, return the maximum number of consecutive1’s in the array if you can flip at mostk0’s. -
Example 1:
Input: nums = [1,1,1,0,0,0,1,1,1,1,0], k = 2
Output: 6
Explanation: [1,1,1,0,0,1,1,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
- Example 2:
Input: nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], k = 3
Output: 10
Explanation: [0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
- Constraints:
1 <= nums.length <= 105nums[i] is either 0 or 1.0 <= k <= nums.length
- See problem on LeetCode.
Solution: Two pointers/Sliding window
-
We have to choose longest consecutive sequence of 1’s with atmost
kzeros (kzeros can be flipped to 1). We can use a sliding window approach for this since the problem is nothing but finding the longest window with atmost k zeros. - We can maintain two pointers
l(left-most window index) andr(right-most window index). We have following possible scenarios -nums[r] == 0: We will try to include this in our window. Here we have two subcases:k != 0: We can just includenums[r]in current window and extend it. We will also decrement k denoting a zero has been picked in the current windowk == 0: Our window already contains maximum zeros (k) allowed. So, we need to shrink our window size from the left till a zero is removed from the other end. Then we can picknums[r]in our window & extend it.kwon’t change since we have popped a zero from left and picked one from right.
nums[r] == 1: We can simply pick this element and extend our window.
- We will keep updating
ansto hold the maximum of window size at any point in time and finally return it.
def longestOnes(self, nums: List[int], k: int) -> int:
n, ans, l = len(nums), 0, 0
for r in range(n):
if nums[r] == 0: # try to pick current 0
if k == 0: # if window already picked k zeros, pop 1 from left and pick this
while nums[l] != 0 : l += 1
l += 1
else:
k-= 1 # otherwise pick it and decrement k
ans = max(ans, r - l + 1) # update ans as max window size till now
return ans
Complexity
- Time: \(O(n)\), where \(n\) is the number of elements in
nums - Space: \(O(1)\)
[1868/Medium] Product of Two Run-Length Encoded Arrays
Problem
- Run-length encoding is a compression algorithm that allows for an integer array
numswith many segments of consecutive repeated numbers to be represented by a (generally smaller) 2D array encoded. Eachencoded[i] = [val_i, freq_i]describes the ith segment of repeated numbers innumswhereval_iis the value that is repeatedfreq_itimes.- For example,
nums = [1,1,1,2,2,2,2,2]is represented by the run-length encoded arrayencoded = [[1,3],[2,5]]. Another way to read this is “three1’s followed by five2’s”.
- For example,
- The product of two run-length encoded arrays
encoded1andencoded2can be calculated using the following steps:- Expand both
encoded1andencoded2into the full arraysnums1andnums2respectively. - Create a new array prodNums of length
nums1.lengthand setprodNums[i] = nums1[i] * nums2[i]. - Compress prodNums into a run-length encoded array and return it.
You are given two run-length encoded arrays
encoded1andencoded2representing full arraysnums1andnums2respectively. Bothnums1andnums2have the same length. Eachencoded1[i] = [val_i, freq_i]describes thei-thsegment ofnums1, and eachencoded2[j] = [val_j, freq_j]describes thej-thsegment ofnums2.
- Expand both
-
Return the product of
encoded1andencoded2. -
Note: Compression should be done such that the run-length encoded array has the minimum possible length.
- Example 1:
Input: encoded1 = [[1,3],[2,3]], encoded2 = [[6,3],[3,3]]
Output: [[6,6]]
Explanation: encoded1 expands to [1,1,1,2,2,2] and encoded2 expands to [6,6,6,3,3,3].
prodNums = [6,6,6,6,6,6], which is compressed into the run-length encoded array [[6,6]].
- Example 2:
Input: encoded1 = [[1,3],[2,1],[3,2]], encoded2 = [[2,3],[3,3]]
Output: [[2,3],[6,1],[9,2]]
Explanation: encoded1 expands to [1,1,1,2,3,3] and encoded2 expands to [2,2,2,3,3,3].
prodNums = [2,2,2,6,9,9], which is compressed into the run-length encoded array [[2,3],[6,1],[9,2]].
- Constraints:
1 <= encoded1.length, encoded2.length <= 105encoded1[i].length == 2encoded2[j].length == 21 <= vali, freqi <= 104 for each encoded1[i].1 <= valj, freqj <= 104 for each encoded2[j].The full arrays that encoded1 and encoded2 represent are the same length.
- See problem on LeetCode.
Solution: Two windows (one-pass)
- Using two pointers to navigate through the two arrays, and doing the multiplication and encoding on the fly. This avoids the need to flatten the array and do element wise multiplication (which is expensive).
- A very straightforward solution is to
- Expand result for
encoded1(O(10^5) * O(10^4) = O(10^9)) - Expand result for
encoded2. - Calculate product of two results.
- Use two pointer to get the final result.
- Expand result for
- Well, the issue of above solution, it will get a TLE (Time Limit Exceeded) error.
O(10^9)is a time complexity evenO(N)solution will get TLE. Thus, we need to do better. - A better solution, instead of expanding the encoded arrays, we can,
- Take two points on each array.
- Each iteration, take the shorter frequency, calculate product and add to ans.
- Don’t forget to deduct current frequency by the smaller frequency (since it’s used), and increment pointers i or j when current frequency is empty.
- Also, handle the situation where current product is same as the previous product.
- The time complexity of the above solution is
O(10^5), the significance of the length of the encoded array. - In the following implementation:
i: Pointer ofencoded1j: Pointer ofencoded2v1: Current value fromencoded1[i]v2: Current value fromencoded2[j]f1: Current frequency ofv1f2: Current frequency ofv2
class Solution:
def findRLEArray(self, encoded1: List[List[int]], encoded2: List[List[int]]) -> List[List[int]]:
i = j = f1 = f2 = v1 = v2 = 0 # Declare variables
m, n, ans = len(encoded1), len(encoded2), []
while i < m or j < n: # Starting two pointers while loop
if not f1 and i < m: # If `f1 == 0`, assign new value and frequency
v1, f1 = encoded1[i]
if not f2 and j < n: # If `f2 == 0`, assign new value and frequency
v2, f2 = encoded2[j]
cur_min, product = min(f1, f2), v1 * v2 # Calculate smaller frequency and product
if ans and ans[-1][0] == product: # If current product is the same as previous one, update previous frequency
ans[-1][1] += cur_min
else: # Other situation, append new pairs
ans.append([product, cur_min])
f1 -= cur_min # Deduct frequency by smaller frequency (used in current round)
f2 -= cur_min
i += not f1 # When frequency is zero, increment pointer by 1
j += not f2
return ans
- Same approach; rehashed:
class Solution:
def findRLEArray(self, encoded1: List[List[int]], encoded2: List[List[int]]) -> List[List[int]]:
product_encoded = []
e1_index = 0
e2_index = 0
while e1_index < len(encoded1) and e2_index < len(encoded2):
e1_val, e1_freq = encoded1[e1_index]
e2_val, e2_freq = encoded2[e2_index]
product_val = e1_val * e2_val
product_freq = min(e1_freq, e2_freq)
encoded1[e1_index][1] -= product_freq
encoded2[e2_index][1] -= product_freq
if encoded1[e1_index][1] == 0:
e1_index += 1
if encoded2[e2_index][1] == 0:
e2_index += 1
# for the first item in the encoded array or
# if the last product is NOT the same as the current product
if not product_encoded or product_encoded[-1][0] != product_val:
product_encoded.append([product_val, product_freq])
else:
# if the last product is same as the current product, add the count of the
# current product to the last product
# we do this because we want the final encoded array to have the minimum
# possible length
product_encoded[-1][1] += product_freq
return product_encoded
Complexity
- Time: \(O(m+n)\) where
mare the number of unique elements inencoded1, andnare unique numbers inencoded2 - Space: \(O(len(encoded1) + len(encoded2))\)