Distilled • LeetCode • Trie
- Pattern: Trie/Prefix Tree
Pattern: Trie/Prefix Tree
[208/Medium] Implement Trie (Prefix Tree)
Problem
-
A trie (pronounced as “try”) or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
-
Implement the Trie class:
Trie()Initializes the trie object.void insert(String word)Inserts the string word into the trie.boolean search(String word)Returns true if the string word is in the trie (i.e., was inserted before), and false otherwise.boolean startsWith(String prefix)Returns true if there is a previously inserted string word that has the prefix prefix, and false otherwise.
-
Example 1:
Input
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
Output
[null, null, true, false, true, null, true]
Explanation
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // return True
trie.search("app"); // return False
trie.startsWith("app"); // return True
trie.insert("app");
trie.search("app"); // return True
- Constraints:
1 <= word.length, prefix.length <= 2000word and prefix consist only of lowercase English letters.At most 3 * 104 calls in total will be made to insert, search, and startsWith.
- See problem on LeetCode.
Solution: Dictionary without a TrieNode class
- There is no need to create a
TrieNodeclass. Using a dictionary can give much better performance. Nodes are replaced by dictionary.is_wordis replaced by adding a-key to the dictionary.
class Trie(object):
def __init__(self):
self.trie = {}
def insert(self, word):
t = self.trie
for c in word:
if c not in t: t[c] = {}
t = t[c]
t["-"] = True
def search(self, word):
t = self.trie
for c in word:
if c not in t: return False
t = t[c]
return "-" in t
def startsWith(self, prefix):
t = self.trie
for c in prefix:
if c not in t: return False
t = t[c]
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Using a TrieNode class
- Using a dictionary to implement a
TrieNodeclass:
class TrieNode:
def __init__(self):
self.childNodes = {}
self.isWordEnd = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word: str) -> None:
"""
we will start with root node and check for the first character
if there is already a node present for the character we will fetch that node, else we will create a new node
then we will iterate to next character
"""
currNode = self.root
for ch in word:
node = currNode.childNodes.get(ch, TrieNode())
currNode.childNodes[ch] = node
currNode = node
# after all the characters are traversed, mark the last node as end of word
currNode.isWordEnd = True
def search(self, word: str) -> bool:
"""
we will start from root node and check for all the characters
if we could not find a node for a character we will return False there
once we iterate through all character we will check if that is a word end
"""
currNode = self.root
for ch in word:
node = currNode.childNodes.get(ch) # or if ch not in currNode.childNodes:
if not node: # return False
return False
currNode = node
return currNode.isWordEnd
def startsWith(self, prefix: str) -> bool:
"""
starts with is similar to search except here we don't have to check whether the last character is end of word
"""
currNode = self.root
for ch in prefix:
node = currNode.childNodes.get(ch)
if not node:
return False
currNode = node
return True
- Using a
defaultdictto implement aTrieNodeclass:
from collections import defaultdict
class TrieNode(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.nodes = defaultdict(TrieNode) # Easy to insert new node.
self.isword = False # True for the end of the trie.
class Trie(object):
def __init__(self):
self.root = TrieNode()
def insert(self, word):
"""
Inserts a word into the trie by creating nodes with individual chars.
:type word: str
:rtype: void
"""
curr = self.root
for char in word:
curr = curr.nodes[char]
curr.isword = True
def search(self, word):
"""
Returns True if the word is in the trie.
:type word: str
:rtype: bool
"""
curr = self.root
for char in word:
if char not in curr.nodes:
return False
curr = curr.nodes[char]
return curr.isword
def startsWith(self, prefix):
"""
Returns if there is any word in the trie
that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
curr = self.root
for char in prefix:
if char not in curr.nodes:
return False
curr = curr.nodes[char]
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[211/Medium] Design Add and Search Words Data Structure
Problem
-
Design a data structure that supports adding new words and finding if a string matches any previously added string.
-
Implement the WordDictionary class:
WordDictionary()Initializes the object.void addWord(word)Adds word to the data structure, it can be matched later.bool search(word)Returns true if there is any string in the data structure that matches word or false otherwise. word may contain dots ‘.’ where dots can be matched with any letter.
-
Example:
Input
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
Output
[null,null,null,null,false,true,true,true]
Explanation
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True
- Constraints:
1 <= word.length <= 25word in addWord consists of lowercase English letters.word in search consist of '.' or lowercase English letters.There will be at most 3 dots in word for search queries.At most 104 calls will be made to addWord and search.
- See problem on LeetCode.
Solution: RegEx
- With dots representing any letter, this problem is basically begging for a regular expression solution :)
class WordDictionary:
def __init__(self):
# use "#" as a delimiter for the beginning and end of the word
self.words = '#'
def addWord(self, word):
self.words += word + '#'
def search(self, word):
return bool(re.search('#' + word + '#', self.words))
- A different approach using
defaultdict:
class WordDictionary:
def __init__(self):
self.words = collections.defaultdict(set)
def addWord(self, word):
# index by the length of the word
self.words[len(word)].add(word)
def search(self, word):
return any(map(re.compile(word).match,
self.words[len(word)]))
Solution: Trie
- Using
TrieNodeclass implemented using adefaultdict:
class TrieNode():
def __init__(self):
self.children = collections.defaultdict(TrieNode)
self.isWord = False
class WordDictionary(object):
def __init__(self):
self.root = TrieNode()
def addWord(self, word):
node = self.root
for w in word:
node = node.children[w]
node.isWord = True
def search(self, word):
node = self.root
self.res = False
self.dfs(node, word)
return self.res
def dfs(self, node, word):
if not word:
if node.isWord:
self.res = True
return
if word[0] == ".":
for n in node.children.values():
self.dfs(n, word[1:])
else:
node = node.children.get(word[0])
if not node:
return
self.dfs(node, word[1:])
- Using
TrieNodeclass implemented using a dictionary. Also, saving index in a stack instead of string slicing:
class WordNode:
def __init__(self):
self.children = {}
self.isEnd = False
class WordDictionary:
def __init__(self):
self.root = WordNode()
def addWord(self, word):
node = self.root
for w in word:
if w in node.children:
node = node.children[w]
else:
node.children[w] = WordNode()
node = node.children[w]
node.isEnd = True
def search(self, word):
stack = [(self.root, word)]
while stack:
node, w = stack.pop()
if not w:
if node.isEnd:
return True
elif w[0] == '.':
for n in node.children.values():
stack.append((n, w[1:]))
else:
if w[0] in node.children:
n = node.children[w[0]]
stack.append((n, w[1:]))
return False
- Same approach; rephrased:
class WordDictionary:
def __init__(self):
self.trie = {}
def addWord(self, word: str) -> None:
node = self.trie
for c in word:
node = node.setdefault(c, {})
node['$'] = True
def search(self, word: str) -> bool:
return self.searchNode(self.trie, word)
def searchNode(self, node, word: str) -> bool:
for i, c in enumerate(word):
if c == '.':
return any(self.searchNode(node[w], word[i+1:]) for w in node if w != '$')
if c not in node: return False
node = node[c]
return '$' in node
- The question is expecting us to design a data structure that supports adding new words and finding if a string matches any previously added string. So, to design a data structure we only need to support three function’s for this data structure:
- One is the constructor that’s gonna initialize the object.
- One is adding the word’s, but all of them are lower case from
atoz. - One is searching a word, and the word can contains any character from
atoz. But there is one additional character it contains, “.” character (the “.” character is a wild card, can match any character easily in the string).
- The brute force way to solve this problem is pretty simple, “having a list of words and then just for every search we would just see, if this search match any of the word in input list.” But it’s not an efficient way, especially in terms of the space complexity involved (storing whole strings and not exploiting the face that common prefixes across strings do not need to be stored again). An efficient way to solve this problem. And for that we require Trie data structure a.k.a. Prefix tree.
- Let’s understand Trie first. Trie is basically a tree where each node holds a character and can have up to
26children in the word add-search context, because we have 26 lower case characters in the alphabet (fromatoz). So, basically each node represents a single character. Graphically speaking:
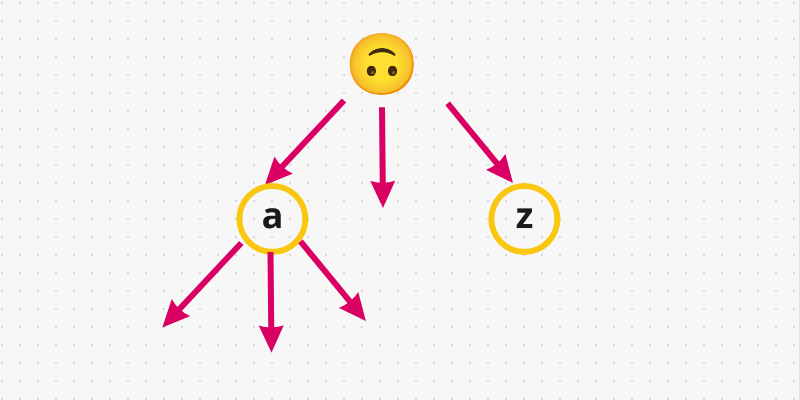
- If we insert the word
abcin our trie,awill havebas a child, which in turn will havecas a child. Graphically, this is how it looks like:
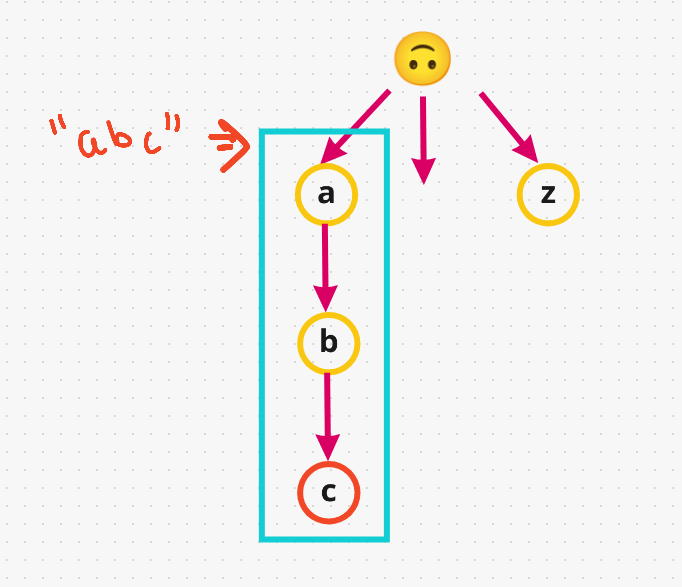
-
Note that in the above example,
cdenotes the end of the word for the wordabc. Now, if we added another word example, sayab, we don’t addaandbback again since they are already available to us. We can simply re-use these characters. So, we have two words along this pathabcandab. Basically, all words that start withaandbwould live in this space, that’s what makes it efficient. Hence, a trie is also called a prefix tree. -
Now let’s take an example and build our tree.
Input
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
Output
[null,null,null,null,false,true,true,true]
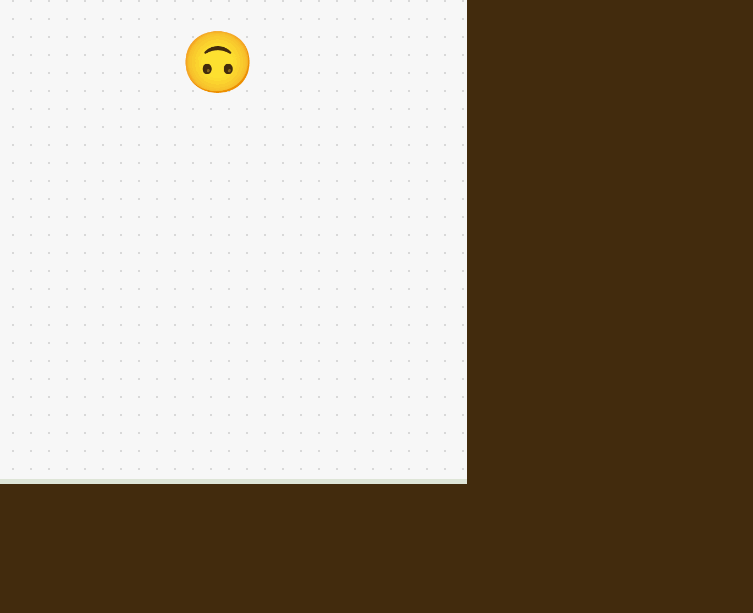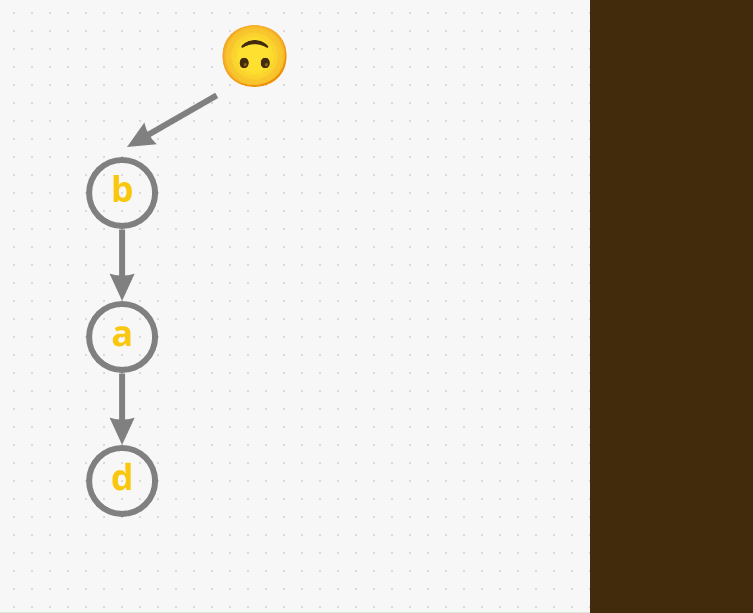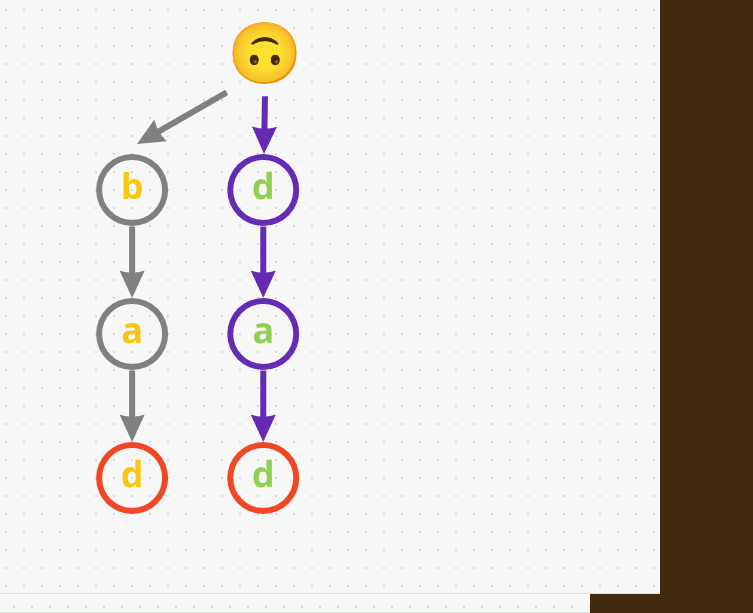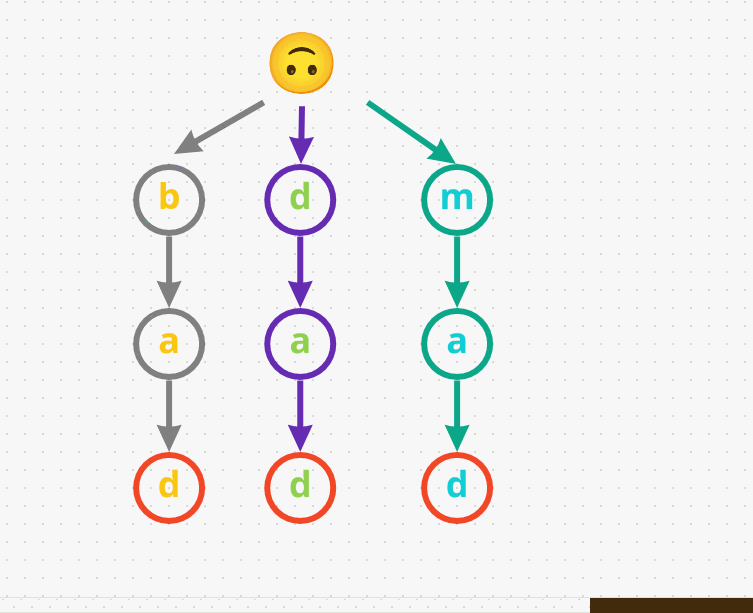
- The first word we add is
bad, i.e.,b->a->d. -
Next, let’s add another word
dad. Given that we don’t share the same prefix as the earlier wordbad(badstarts withb, whiledadstarts withd), we have to start with a different path. So, let’s adddadasd->a->d. - We have one last word before we start searching, say
mad. So, we don’t havem, then let’s add it:m->a->d
- So far we have three word’s and all of them end with a different
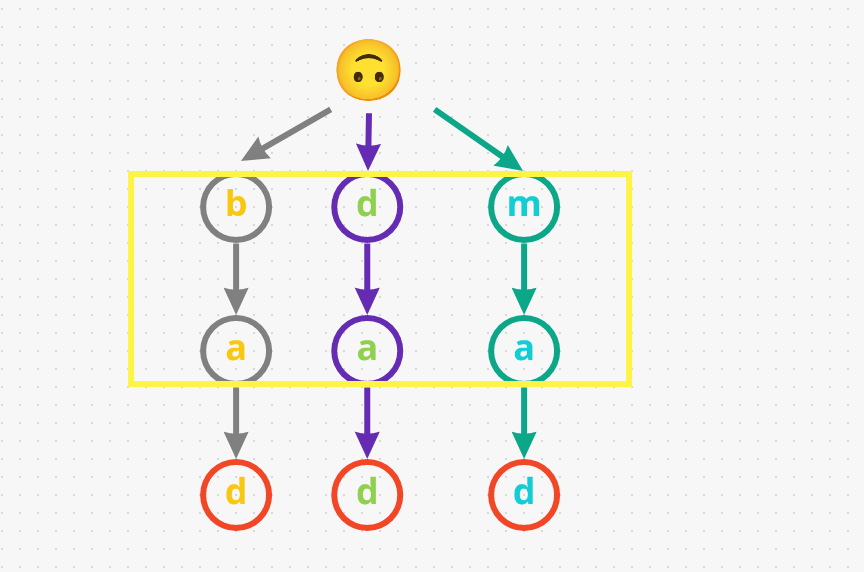
d. But all three of them have different prefixes that’s why they are along different path’s:
-
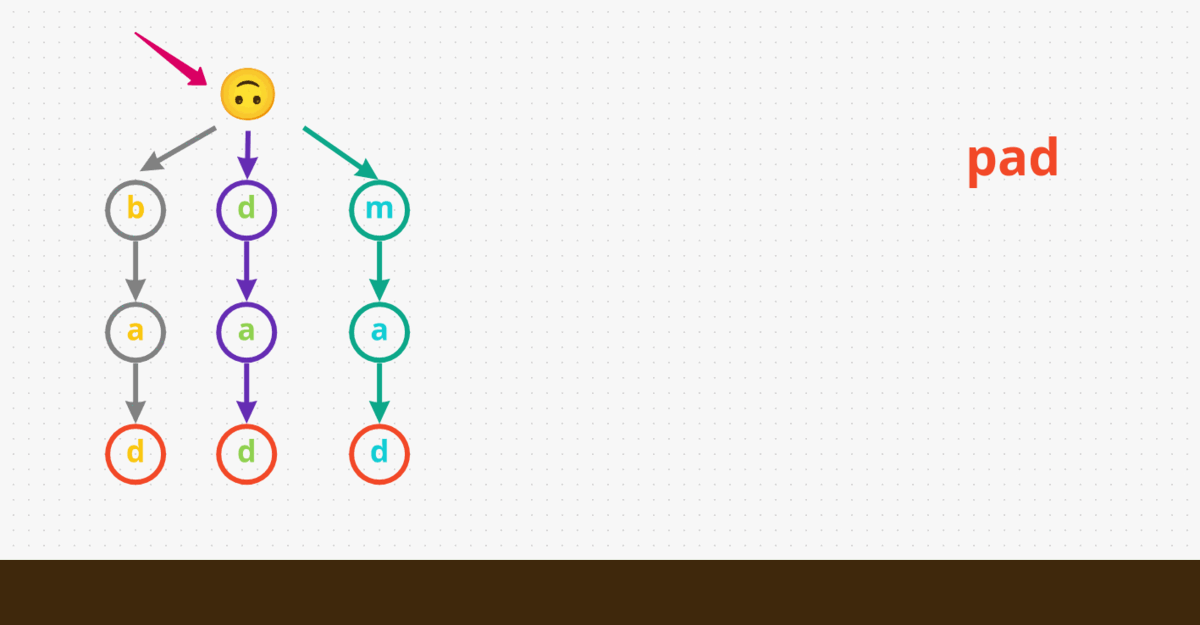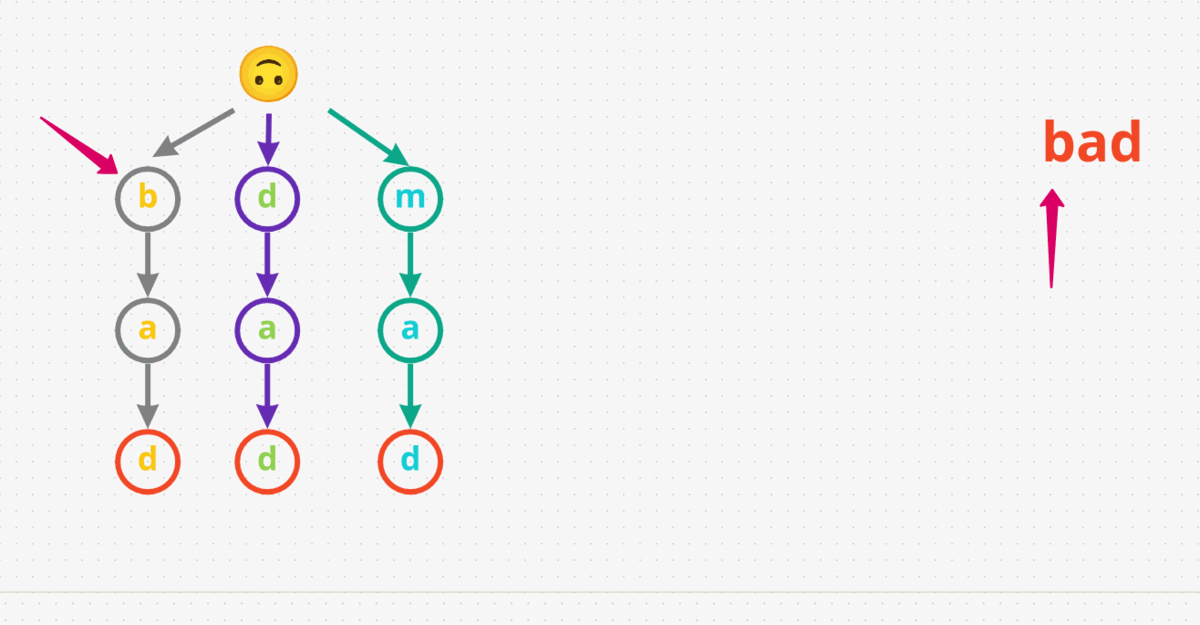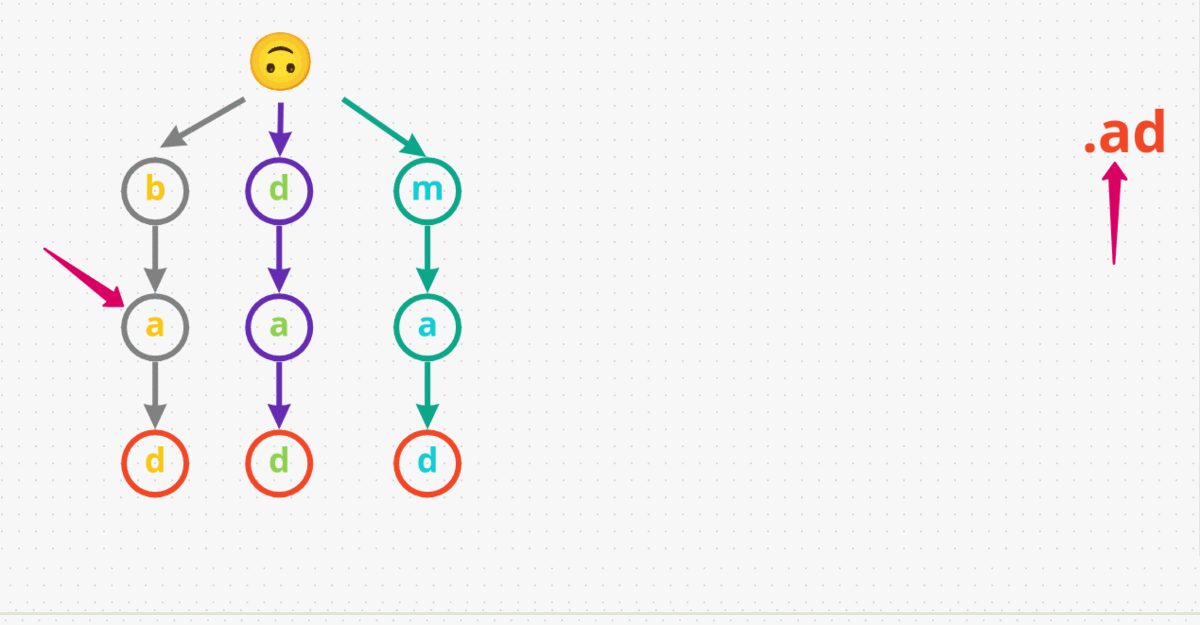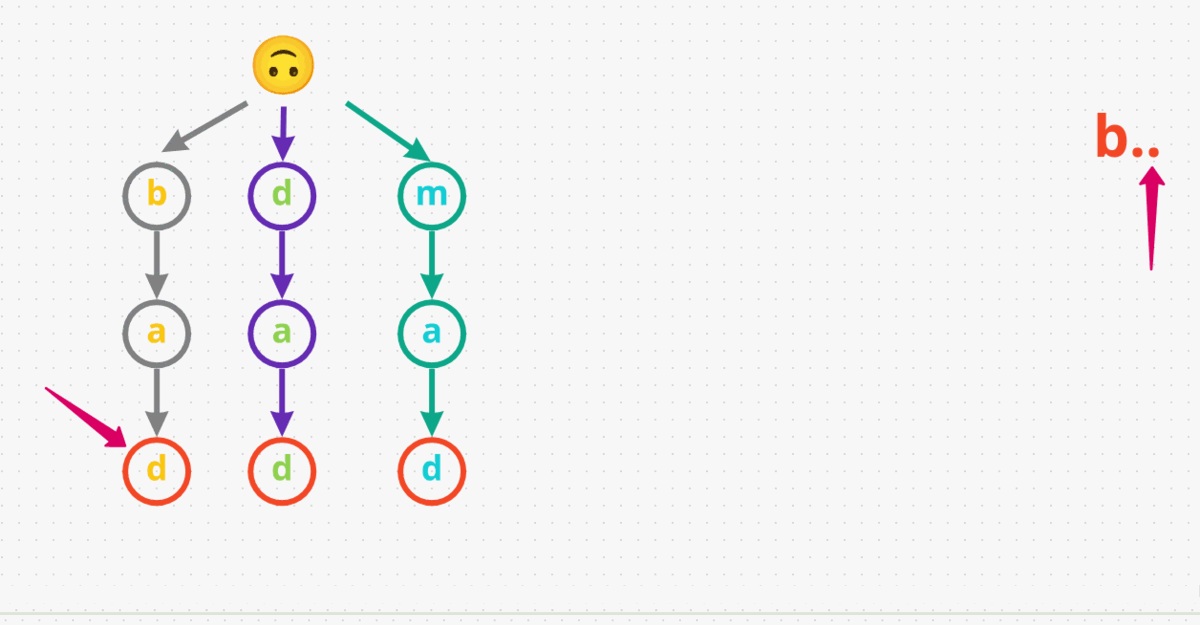
Now let’s look at the searching path:
- The first word we gonna search for is
pad. We start at the root and and begin looking for the first character in the word, i.e.,p. We immediately returnFalseaspdoesn’t even exist in our input. - Now, let’s search for another word
bad. We start at the root and see there are any nodes withb. Yes, we haveb. Now let’s check doesbhave a childa, which it does. For the last characterd, let’s check ifahas a childd, and surely it does! Lastly we have to say the last characterdis in our Trie, which designated as the end of the word (marked red in the diagram below). Therefore, we returnTruefor the inputbad. - Let’s search for
.adnext. The dot.character matches any character. We start at the root and go through all possible paths using a DFS or backtracking approach. So, let’s say we start with going downbas the first node. Check ifbhas a childa, which it does. Now, check ifahas a childd, which it also does. Lastly, note that the last characterdin our Trie is designated as the end of the word. Therefore, we returnTruefor this input.ad. - Let’s try one last search, looking for
b... So, we start at the root and see there are any nodes withb. Yes, we haveb. Now, check if we have a character underbto match., which we have asa. Now, we’re looking for a character for our last dot.. Yes we havedand it is the end of the word. Therefore, we returnTruefor this inputb...
- The first word we gonna search for is
-
Here’s a visual demonstration for the overall process:
Solution: Trie using TrieNode class
class WordDictionary:
def __init__(self):
# Initialize your data structure here.
self.children = [None]*26
self.isEndOfWord = False
def addWord(self, word: str) -> None:
# Adds a word into the data structure.
curr = self
for c in word:
if curr.children[ord(c) - ord('a')] == None:
curr.children[ord(c) - ord('a')] = WordDictionary()
curr = curr.children[ord(c) - ord('a')]
curr.isEndOfWord = True;
def search(self, word: str) -> bool:
# Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
curr = self
for i in range(len(word)):
c = word[i]
if c == '.':
for ch in curr.children:
if ch != None and ch.search(word[i+1:]): return True
return False
if curr.children[ord(c) - ord('a')] == None: return False
curr = curr.children[ord(c) - ord('a')]
return curr != None and curr.isEndOfWord
Complexity
- Time: \(O(m)\) for well defined words, but in the worse case \(O(m \cdot 26^n)\) where \(m\) is the total queries and \(n\) being the length of the input string
- To understand the worst case time complexity, consider the input
.......and the trie is almost complete till a deep enough level. In this case, chances are you have to iterate over 26 character for each node. That boils down the time complexity to be \(O(m \cdot 26^n)\)
- To understand the worst case time complexity, consider the input
- Space: \(O(1)\) for well defined words, but for worst case \(O(m)\)
[616/758/Medium] Add Bold Tag in String
Problem
-
You are given a string s and an array of strings words. You should add a closed pair of bold tag
<b>and</b>to wrap the substrings insthat exist in words. If two such substrings overlap, you should wrap them together with only one pair of closed bold-tag. If two substrings wrapped by bold tags are consecutive, you should combine them. -
Return
safter adding the bold tags. -
Example 1:
Input: s = "abcxyz123", words = ["abc","123"]
Output: "<b>abc</b>xyz<b>123</b>"
- Example 2:
Input: s = "aaabbcc", words = ["aaa","aab","bc"]
Output: "<b>aaabbc</b>c"
- Constraints:
1 <= s.length <= 10000 <= words.length <= 1001 <= words[i].length <= 1000s and words[i] consist of English letters and digits.All the values of words are unique.
- See problem on LeetCode.
Solution: Window-based method to find all open/close tags, sort by (index, open tag), merge tags with deque
- First find all open and close tags, and sort by index and then open tag first.
- Similar to Meeting Rooms II, merging tags and keep only valid, non-nested tags.
- Apply valid tags on original string.
class Solution:
def addBoldTag(self, s: str, words: List[str]) -> str:
windows = set([len(word) for word in words]) # get unique window length (reduce iteration), O(m)
words = set(words) # convert `words` to hash set for faster search, O(m)
n = len(s)
tag_list = []
for window in windows: # for each window size, O(m)
for i in range(n-window+1): # for each word at this size, O(n)
if s[i:i+window] in words: # see if each word at current window size is in the set
tag_list.append((i, 1)) # append open tag index, 1 meaning open tag
tag_list.append((i+window, -1)) # append close tag index, -1 meaning close tag
tag_list.sort(key=lambda x: (x[0], -x[1])) # sort by index & open tag first, O(n*logn)
dq = collections.deque()
cnt = 0
for idx, sign in tag_list: # merging tags, O(n)
if not cnt: # if no open tags, add open tag
cnt += 1
dq.append(idx)
elif cnt == 1 and sign == -1: # append close tag only when previous tag is open tag (no nested tags)
cnt -= 1
dq.append(idx)
else: # any other cases, only count tags, not append any
cnt += 1 if sign == 1 else -1
ans = ''
open_tag = True
for i, c in enumerate(s): # apply tags on original string `s`, O(n)
if dq and i == dq[0]: # add tags
ans += '<b>' if open_tag else '</b>'
open_tag = not open_tag
dq.popleft() # remove used tag
ans += c
return ans + '</b>' if dq else ans # add ending tag if there is one
Complexity
- Time: \(O(m*n), m = len(words), n = len(s)\)
- Space: \(O(n)\)
Solution: Using RegEx
- Similar idea but using regex and sorted based on
lento avoid prefix match first.
from re import escape, finditer
class Solution:
def merge_spans(self, spans: list[list[int]]) -> list[list[int]]:
overlap = lambda a, b: a[0] <= b[1] and a[1] >= b[0]
output = []
for span in spans:
if output and overlap(output[-1], span):
output[-1] = [min(output[-1][0], span[0]), max(output[-1][1], span[1])]
else:
output.append(span)
return output
def addBoldTag(self, s: str, dict: list[str]) -> str:
pattern = r"(?=({}))".format("|".join(map(escape, sorted(dict, key=len, reverse=True))))
spans = self.merge_spans([m.span(1) for m in finditer(pattern, s) if m.group(1)])
for i, span in enumerate(spans):
span = [span[0] + i * 7, span[1] + i * 7]
s = s[: span[0]] + "<b>" + s[span[0] : span[1]] + "</b>" + s[span[1] :]
return s
Solution: Trie Tree and Merge Intervals
- Trie tree is used to speed up string match (faster than
findorstartwithin large query request). - Using Merge Intervals instead of mask to reduce Time and Space Complexity, both from
O(n)toO(m), wheremrepresents interval numbers after merged.
class Solution:
def addBoldTag(self, s: str, dict: 'List[str]') -> str:
trie, n, intervals, res = {}, len(s), [], ""
# create trie tree
for w in dict:
cur = trie
for c in w:
cur = cur.setdefault(c, {})
cur["#"] = 1
# interval merge
def add_interval(interval):
if intervals and intervals[-1][1] >= interval[0]:
if intervals[-1][1] < interval[1]:
intervals[-1][1] = interval[1]
else:
intervals.append(interval)
# make max match and add to interval
for i in range(n):
cur, max_end = trie, None
for j in range(i, n):
if s[j] not in cur:
break
cur = cur[s[j]]
if "#" in cur:
max_end = j + 1
# just need to add max-match interval
if max_end:
add_interval([i, max_end])
# concat result
res, prev_end = "", 0
for start, end in intervals:
res += s[prev_end:start] + '<b>' + s[start:end] + "</b>"
prev_end = end
return res + s[prev_end:]
[616/758/Medium] Design Search Autocomplete System
Problem
-
Design a search autocomplete system for a search engine. Users may input a sentence (at least one word and end with a special character
'#'). -
You are given a string array sentences and an integer array
timesboth of lengthnwheresentences[i]is a previously typed sentence andtimes[i]is the corresponding number of times the sentence was typed. For each input character except'#', return the top 3 historical hot sentences that have the same prefix as the part of the sentence already typed. -
Here are the specific rules:
- The hot degree for a sentence is defined as the number of times a user typed the exactly same sentence before.
- The returned top 3 hot sentences should be sorted by hot degree (The first is the hottest one). If several sentences have the same hot degree, use ASCII-code order (smaller one appears first).
- If less than 3 hot sentences exist, return as many as you can.
- When the input is a special character, it means the sentence ends, and in this case, you need to return an empty list.
- Implement the AutocompleteSystem class:
- AutocompleteSystem(String[] sentences, int[] times) Initializes the object with the sentences and times arrays.
- List
input(char c) This indicates that the user typed the character c. - Returns an empty array [] if c == ‘#’ and stores the inputted sentence in the system.
- Returns the top 3 historical hot sentences that have the same prefix as the part of the sentence already typed. If there are fewer than 3 matches, return them all.
- Example 1:
Input
["AutocompleteSystem", "input", "input", "input", "input"]
[[["i love you", "island", "iroman", "i love leetcode"], [5, 3, 2, 2]], ["i"], [" "], ["a"], ["#"]]
Output
[null, ["i love you", "island", "i love leetcode"], ["i love you", "i love leetcode"], [], []]
Explanation
AutocompleteSystem obj = new AutocompleteSystem(["i love you", "island", "iroman", "i love leetcode"], [5, 3, 2, 2]);
obj.input("i"); // return ["i love you", "island", "i love leetcode"]. There are four sentences that have prefix "i". Among them, "ironman" and "i love leetcode" have same hot degree. Since ' ' has ASCII code 32 and 'r' has ASCII code 114, "i love leetcode" should be in front of "ironman". Also we only need to output top 3 hot sentences, so "ironman" will be ignored.
obj.input(" "); // return ["i love you", "i love leetcode"]. There are only two sentences that have prefix "i ".
obj.input("a"); // return []. There are no sentences that have prefix "i a".
obj.input("#"); // return []. The user finished the input, the sentence "i a" should be saved as a historical sentence in system. And the following input will be counted as a new search.
- Constraints:
n == sentences.lengthn == times.length1 <= n <= 1001 <= sentences[i].length <= 1001 <= times[i] <= 50c is a lowercase English letter, a hash '#', or space ' '.Each tested sentence will be a sequence of characters c that end with the character '#'.Each tested sentence will have a length in the range [1, 200].The words in each input sentence are separated by single spaces.At most 5000 calls will be made to input.
- See problem on LeetCode.
Solution:
- Explanation:
- At each prefix, store 3 most frequent sentences. It trades off space for better time complexity.
- See below comments for more explanation
- Implementation:
class TrieNode:
def __init__(self):
self.children = dict()
self.three = [] # three sentences
class Trie:
def __init__(self):
self.root = TrieNode()
def add(self, sentence, time):
node = self.root
for c in sentence:
if c not in node.children:
node.children[c] = TrieNode()
node = node.children[c]
for i, (t, s) in enumerate(node.three): # update three sentences
if s == sentence:
tmp = node.three[:]
tmp[i][0] = time
break
else:
tmp = node.three + [[time, sentence]]
node.three = sorted(tmp, key=lambda x: (-x[0], x[1]))[:3]
class AutocompleteSystem:
def __init__(self, sentences: List[str], times: List[int]):
self.d = collections.Counter() # keep tracking {sentence: time}
self.trie = Trie() # trie
self.node = self.trie.root # pointer to root and move along with input characters
for sentence, time in zip(sentences, times): # add initial info
self.d[sentence] += time
self.trie.add(sentence, time)
self.cur = '' # prefix
self.prefix_none = False # True if prefix cannot be found
def input(self, c: str) -> List[str]:
if c == '#': # input ends
self.node = self.trie.root # reset self.node to root
self.d[self.cur] += 1 # increment counter by 1
self.trie.add(self.cur, self.d[self.cur]) # update sentence and time
self.cur = '' # reset prefix string
self.prefix_none = False # reset this flag
return [] # return
self.cur += c # making prefix
if c not in self.node.children or self.prefix_none: # when prefix is not found the first time and time after 1st time
self.prefix_none = True # set flag
return []
self.prefix_none = False # reset prefix_none flag
self.node = self.node.children[c] # move to next node
return [word for _, word in self.node.three] # return 3 words
- Similar approach; rehashed:
- We first build a trie for the given sentences and times. Note that we negate hot so that we can easily return the Top 3 hot sentences after sorting them in ascending order.
- We initialize the following three variables to keep track of search state. They will be reset when the user types #:
search_termis used to track the current input.last_nodestores the previous node when we search in trie. It ensures that we do not always start searching from trie root when there are sentences that match the current input.no_matchis a flag. It ensures that we skip searching once there are no sentences that match the current input. The user can still type and we will record the input insearch_term.
- We only perform searching if the latest input character is in
last_node’s children.
class TrieNode:
def __init__(self):
self.children = {}
self.is_sentence = False
self.hot = 0
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, sentence, hot):
node = self.root
for char in sentence:
if not char in node.children:
node.children[char] = TrieNode()
node = node.children[char]
node.is_sentence = True
node.hot -= hot
class AutocompleteSystem:
def __init__(self, sentences: List[str], times: List[int]):
self.build_trie(sentences, times)
self.reset_search()
def build_trie(self, sentences, times):
self.trie = Trie()
for i, sentence in enumerate(sentences):
self.trie.insert(sentence, times[i])
def reset_search(self):
self.search_term = ""
self.last_node = self.trie.root
self.no_match = False
def input(self, c: str) -> List[str]:
if c == "#":
self.trie.insert(self.search_term, 1)
self.reset_search()
else:
self.search_term += c
if not c in self.last_node.children or self.no_match:
self.no_match = True
return []
self.last_node = self.last_node.children[c]
result = []
self.dfs(self.last_node, self.search_term, result)
return [sentences[1] for sentences in sorted(result)[:3]]
def dfs(self, node, path, result):
if node.is_sentence:
result.append((node.hot, path))
for char in node.children:
self.dfs(node.children[char], path+char, result)