Pattern: Stack

[20/Easy] Valid Parentheses

  • Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

  • An input string is valid if:
    • Open brackets must be closed by the same type of brackets.
    • Open brackets must be closed in the correct order.
  • Example 1:
Input: s = "()"
Output: true
  • Example 2:
Input: s = "()[]{}"
Output: true
  • Example 3:
Input: s = "(]"
Output: false
  • Constraints:
    • 1 <= s.length <= 104
    • s consists of parentheses only '()[]{}'.
  • See problem on LeetCode.

Problem

Solution: Stack

class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        
        for paren in s:
            if paren in "({[":
                stack.append(paren)
            elif not stack:
                return False
            elif paren == ")":
                if stack.pop() != "(":
                    return False
            elif paren == "}":
                if stack.pop() != "{":
                    return False
            elif paren == "]":
                if stack.pop() != "[":
                    return False

        return not len(stack)
  • Same approach; concise:
class Solution:
    def isValid(self, s: str) -> bool:
        if len(s)%2:
            return False
        
        d = {'(':')', '{':'}','[':']'}
        stack = []
        for char in s:
            if char in d:
                stack.append(char)
            
            # "not len(stack)" is used to ensure we don't pop an empty list
            elif not len(stack) or d[stack.pop()] != char:
                return False
            
        return not len(stack)
Complexity
  • Time: \(O(n)\)
  • Space: \(O(1)\)

[32/Hard] Longest Valid Parentheses

Problem

  • Given a string containing just the characters ( and ), find the length of the longest valid (well-formed) parentheses substring.

  • Example 1:

Input: s = "(()"
Output: 2
Explanation: The longest valid parentheses substring is "()".
  • Example 2:
Input: s = ")()())"
Output: 4
Explanation: The longest valid parentheses substring is "()()".
  • Example 3:
Input: s = ""
Output: 0
  • Constraints:
    • 0 <= s.length <= 3 * 10^4
    • s[i] is '(', or ')'.
  • See problem on LeetCode.

Solution: Stack

  • One of the key things to realize about valid parentheses strings is that they’re entirely self-satisfied, meaning that while you can have one parentheses substring that is entirely inside another, you can’t have two parentheses substrings that only partially overlap.

  • This means that we can use a greedy \(O(n)\) time complexity solution to this problem without the need for any kind of backtracking. In fact, we should be able to use a very standard stack-based valid parentheses string algorithm with just three very minor modifications.

  • In a standard valid parentheses string algorithm, we iterate through the string (s) and push the index (i) of any ( to our stack. Whenever we find a ), we match it with the last entry on the stack and pop said entry off. We know the string is not valid if we find a ) while there are no ( indexes in the stack with which to match it, and also if we have leftover ( in the stack when we reach the end of s.

  • For this problem, we will need to add in a step that updates our answer (max_length) when we close a parentheses pair. Since we stored the index of the ( in our stack, we can easily find the difference between the ) at i and the last entry in the stack, which should be the length of the valid substring which was just closed.

  • But here we run into a problem, because consecutive valid parentheses substrings can be grouped into a larger valid parentheses substring (i.e., ()() = 4). So instead of counting from the last stack entry, we should actually count from the second to last entry, to include any other valid closed parentheses substrings since the most recent ( that will still remain after we pop the just-matched last stack entry off.

  • This, of course, brings us to the second and third changes. Since we’re checking the second to last stack entry, what happens in the case of ()() when you close the second valid substring yet there’s only the one stack entry left at the time?

  • To avoid this issue, we can just wrap the entire string in another imaginary set of parentheses by starting with stack = [-1], indicating that there’s an imaginary ( just before the beginning of the string at i = 0.

  • The other issue is that we will want to continue even if the string up to i becomes invalid due to a ) appearing when the stack is “empty”, or in this case has only our imaginary index left. In that case, we can just effectively restart our stack by updating our imaginary ( index (stack[0] = i) and continue on.

  • Then, once we reach the end of s, we can just return ans.

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        # stack, used to record index of parenthesis
        # initialized to -1 as dummy head for valid parentheses length computation
        # for the case of consecutive valid parentheses substrings being grouped 
        # into a larger valid parentheses substring (for e.g., `()()` = 4)
        stack = [-1]
        
        max_length = 0
        
        # linear scan each index and character in input string s
        for cur_idx, char in enumerate(s):
            
            if char == '(':
                # push when current char is "("
                stack.append(cur_idx)
                
            else:
                
                # pop when current char is ")"
                stack.pop()
                
                if not stack:
                    # stack is empty, push current index into stack
                    stack.append(cur_idx)
                else:
                    # stack is non-empty, update max valid parentheses length
                    max_length = max(max_length, cur_idx - stack[-1])
                
        return max_length
Complexity
  • Time: \(O(n)\) where \(n\) is the number of characters in the input string, i.e., n = len(s).
  • Space: \(O(n)\) for stack

Solution: Stack

  • Cleaner; doesn’t need stack initialization as in the previous solution.
  • Algorithm:
    • Whenever we see a new open paren, we push the current longest streak to the stack.
    • Whenever we see a close paren, we pop the top value if possible, and add the value (which was the previous longest streak up to that point) to the current one (because they are now contiguous) and add 2 to count for the matching open and close parens.
    • If there is no matching open paren for a close paren, reset the current count.
class Solution:
    def longestValidParentheses(self, s: str) -> int:
        stack, curr_longest, max_longest = [], 0, 0
        
        for c in s:
            if c == '(':
                stack.append(curr_longest)
                curr_longest = 0
            elif c == ')':
                if stack:
                    curr_longest += stack.pop() + 2
                    max_longest = max(max_longest, curr_longest)
                else:
                    curr_longest = 0
                    
        return max_longest
Complexity
  • Time: \(O(n)\) where \(n\) is the number of characters in the input string, i.e., n = len(s).
  • Space: \(O(n)\) for stack

[71/Medium] Simplify Path

Problem

  • Given a string path, which is an absolute path (starting with a slash /) to a file or directory in a Unix-style file system, convert it to the simplified canonical path.
  • In a Unix-style file system, a period . refers to the current directory, a double period .. refers to the directory up a level, and any multiple consecutive slashes (i.e. //) are treated as a single slash /. For this problem, any other format of periods such as ... are treated as file/directory names.
  • The canonical path should have the following format:
    • The path starts with a single slash /.
    • Any two directories are separated by a single slash /.
    • The path does not end with a trailing /.
    • The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period . or double period ..)

  • Return the simplified canonical path.

  • Example 1:
Input: path = "/home/"
Output: "/home"
Explanation: Note that there is no trailing slash after the last directory name.
  • Example 2:
Input: path = "/../"
Output: "/"
Explanation: Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
  • Example 3:
Input: path = "/home//foo/"
Output: "/home/foo"
Explanation: In the canonical path, multiple consecutive slashes are replaced by a single one.
  • Constraints:
    • 1 <= path.length <= 3000
    • path consists of English letters, digits, period '.', slash '/' or '_'.
    • path is a valid absolute Unix path.
  • See problem on LeetCode.

Solution: Stack

class Solution:
    def simplifyPath(self, path: str) -> str:
        stack = []
        for token in path.split('/'):
            if token in ('', '.'): # if not token or token == ".":  # skip current dir
                continue           # or pass
            elif token == '..':
                if stack:          # if we're not in the root directory, go back; else don't do anything 
                    stack.pop()    # (since "cd .." on root, does nothing)
            else:
                stack.append(token)
                
        return '/' + '/'.join(stack)
Complexity
  • Time: \(O(n)\) where \(n\) is the number of characters in the input string, i.e., n = len(path).
  • Space: \(O(n)\)

[232/Easy] Implement Queue using Stacks

Problem

  • Implement a first in first out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue (push, peek, pop, and empty).

  • Implement the MyQueue class:
    • void push(int x) Pushes element x to the back of the queue.
    • int pop() Removes the element from the front of the queue and returns it.
    • int peek() Returns the element at the front of the queue.
    • boolean empty() Returns true if the queue is empty, false otherwise.
  • Notes:
    • You must use only standard operations of a stack, which means only push to top, peek/pop from top, size, and is empty operations are valid.
    • Depending on your language, the stack may not be supported natively. You may simulate a stack using a list or deque (double-ended queue) as long as you use only a stack’s standard operations.
  • Example 1:
Input
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
Output
[null, null, null, 1, 1, false]
  • Explanation: 
    MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false
  • Constraints:
    • 1 <= x <= 9
    • At most 100 calls will be made to push, pop, peek, and empty.
    • All the calls to pop and peek are valid.

  • Follow-up: Can you implement the queue such that each operation is amortized O(1) time complexity? In other words, performing n operations will take overall O(n) time even if one of those operations may take longer.

  • See problem on LeetCode.

Solution: Stack

class MyQueue:
    def __init__(self):
        self.stack = []

    def push(self, x: int) -> None:
        self.stack += [x] # or self.stack.append(x) 

    def pop(self) -> int:
        return self.stack.pop(0)

    def peek(self) -> int:
        return self.stack[0]

    def empty(self) -> bool:
        return len(self.stack) == 0
        
# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()
Complexity
  • Time: \(O(n)\) because of pop(0).
  • Space: \(O(1)\)

Solution: Stack with Index Book-keeping

class MyQueue:
    def __init__(self):
        self.stack = []
        self.idx = 0

    def push(self, x: int) -> None:
        self.stack += [x]

    def pop(self) -> int:
        self.idx += 1
        return self.stack[self.idx-1]
        
    def peek(self) -> int:
        return self.stack[self.idx]
        
    def empty(self) -> bool:
        return self.idx == len(self.stack)

# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()
Complexity
  • Time: \(O(1)\)
  • Space: \(O(1)\)

[227/Medium] Basic Calculator II

Problem

  • Given a string s which represents an expression, evaluate this expression and return its value.
  • The integer division should truncate toward zero.
  • You may assume that the given expression is always valid. All intermediate results will be in the range of [-2^31, 2^31 - 1].

  • Note: You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as eval().

  • Example 1:
Input: s = "3+2*2"
Output: 7
  • Example 2:
Input: s = " 3/2 "
Output: 1
  • Example 3:
Input: s = " 3+5 / 2 "
Output: 5
  • Constraints:
    • 1 <= s.length <= 3 * 105
    • s consists of integers and operators ('+', '-', '*', '/') separated by some number of spaces.
    • s represents a valid expression.
    • All the integers in the expression are non-negative integers in the range [0, 2^31 - 1].
    • The answer is guaranteed to fit in a 32-bit integer.
  • See problem on LeetCode.

Solution: Stack

class Solution:
    def calculate(self, s):
        if not s:
            return "0"
                    
        num, stack, sign = 0, [], "+"
        for i in range(len(s)):
            if s[i].isdigit():
                num = num * 10 + int(s[i]) # or num = num*10 + ord(s[i]) - ord("0")
            if s[i] in "+-*/" or i == len(s) - 1:
                if sign == "+":
                    stack.append(num)
                elif sign == "-":
                    stack.append(-num)
                elif sign == "*":
                    stack.append(stack.pop()*num)
                else:
                    stack.append(int(stack.pop()/num))
                num = 0
                sign = s[i]
        return sum(stack)
Complexity
  • Time: \(O(n)\)
  • Space: \(O(1)\)

[301/Hard] Remove Invalid Parentheses

  • Given a string s that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.

  • Return all the possible results. You may return the answer in any order.

  • Example 1:

Input: s = "()())()"
Output: ["(())()","()()()"]
  • Example 2:
Input: s = "(a)())()"
Output: ["(a())()","(a)()()"]
  • Example 3:
Input: s = ")("
Output: [""]
  • Constraints:
    • 1 <= s.length <= 25
    • s consists of lowercase English letters and parentheses '(' and ')'.
    • There will be at most 20 parentheses in s.
  • See problem on LeetCode.

Solution: BFS

  • Being lazy and using eval for checking:
def removeInvalidParentheses(self, s):
    level = {s}
    while True:
        valid = []
        for s in level:
            try:
                eval('0,' + filter('()'.count, s).replace(')', '),'))
                valid.append(s)
            except:
                pass
        if valid:
            return valid
        level = {s[:i] + s[i+1:] for s in level for i in range(len(s))}

Solution: BFS

  • Three times as fast as the previous one:
def removeInvalidParentheses(self, s):
    def isvalid(s):
        ctr = 0
        for c in s:
            if c == '(':
                ctr += 1
            elif c == ')':
                ctr -= 1
                if ctr < 0:
                    return False
        return ctr == 0
    level = {s}
    while True:
        valid = filter(isvalid, level)
        if valid:
            return valid
        level = {s[:i] + s[i+1:] for s in level for i in range(len(s))}

Solution: BFS

  • Just a mix of the above two:
def removeInvalidParentheses(self, s):
    def isvalid(s):
        try:
            eval('0,' + filter('()'.count, s).replace(')', '),'))
            return True
        except:
            pass
    level = {s}
    while True:
        valid = filter(isvalid, level)
        if valid:
            return valid
        level = {s[:i] + s[i+1:] for s in level for i in range(len(s))}

Solution: BFS

def removeInvalidParentheses(self, s):
    def isvalid(s):
        s = filter('()'.count, s)
        while '()' in s:
            s = s.replace('()', '')
        return not s
        
    level = {s}
    while True:
        valid = filter(isvalid, level)
        if valid:
            return valid
        level = {s[:i] + s[i+1:] for s in level for i in range(len(s))}

Solution: Stack + Backtracking/DFS

  1. Use a stack to find invalid left and right braces.
  2. If its close brace is at index i, you can remove it directly to make it valid and also you can also remove any of the close braces before that i.e in the range [0, i-1].
  3. Similarly for open brace, left over at index i, you can remove it or any other open brace after that, i.e., [i+1, end].
  4. If left over braces are more than 1 say 2 close braces here, you need to make combinations of all 2 braces before that index and find valid parentheses.
  5. So, we count left and right invalid braces and do backtracking to remove them.
class Solution:
    def removeInvalidParentheses(self, s: str) -> List[str]:
       def isValid(s):
            stack = []
            for i in range(len(s)):
                if( s[i] == '(' ):
                    stack.append( (i,'(') )
                elif( s[i] == ')' ):
                    if(stack and stack[-1][1] == '('):
                        stack.pop()
                    else:
                        stack.append( (i,')') ) # pushing invalid close braces also
            return len(stack) == 0, stack
        
        
        def dfs(s, left, right):
            visited.add(s)
            if left == 0 and right == 0 and isValid(s)[0]:  res.append(s)
            for i, ch in enumerate(s):
                if ch != '(' and ch != ')': continue                                 # if it is any other char ignore.
                if (ch == '(' and left == 0) or (ch == ')' and right == 0): continue # if left == 0 then removing '(' will only cause imbalance. Hence, skip.
                if s[:i] + s[i+1:] not in visited:
                    dfs( s[:i] + s[i+1:], left - (ch == '('), right - (ch == ')') )
        
        stack = isValid(s)[1]
        lc = sum([1 for val in stack if val[1] == "("]) # num of left braces
        rc = len(stack) - lc
        
        res, visited = [], set()
        dfs(s, lc, rc)
        return res
Complexity
  • Time: \(O(2^n)\) since each brace has two options: exits or to be removed.
  • Space: \(O(n)\)

[394/Medium] Decode String

Problem

  • Given an encoded string, return its decoded string.

  • The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.

  • You may assume that the input string is always valid; there are no extra white spaces, square brackets are well-formed, etc.

  • Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there will not be input like 3a or 2[4].

  • Example 1:

Input: s = "3[a]2[bc]"
Output: "aaabcbc"
  • Example 2:
Input: s = "3[a2[c]]"
Output: "accaccacc"
  • Example 3:
Input: s = "2[abc]3[cd]ef"
Output: "abcabccdcdcdef"
  • Constraints:
    • 1 <= s.length <= 30
    • s consists of lowercase English letters, digits, and square brackets '[]'.
    • s is guaranteed to be a valid input.
    • All the integers in s are in the range [1, 300].
  • See problem on LeetCode.

Solution: Backtracking/DFS

class Solution:
def decodeString(self, s: str) -> str:       
    def dfs(s,p):
        res = ""
        i, num = p, 0
        
        while i < len(s):
            asc = (ord(s[i])-48)
            if 0 <= asc <= 9: # can also be written as if s[i].isdigit()
                num = num*10 + asc
            elif s[i] == "[":
                local, pos = dfs(s, i+1)
                res += local*num
                i = pos
                num = 0
            elif s[i] == "]":
                return res, i
            else:
                res += s[i]
            i += 1
            
        return res,i
    
    return dfs(s, 0)[0]
Complexity
  • Time: \(O(n^2)\)
  • Space: \(O(n)\)

Solution: Stack

  • Using a stack to store the previously stored string and the number which we have to use instantly after bracket(if any) gets closed.

  • Possible inputs are: [ , ], alphabet(s) or numbers. Lets talk about each one by one.

    • We will start for loop for traversing through each element of s. If we encounter a number, it will be handled by checking the isdigit() condition. curNum10+int(c) helps in storing the number in curNum , when the number is more than single digit.
    • When we encounter a character, we will start it adding to a string named curString. The character can be single or multiple. curString+=c will keep the character string.
    • The easy part is over.Now, when we encounter [ it means a start of a new substring, meaning the previous substring (if there was one) has already been traversed and handled. So , we will append the current curString and curNum to stack and, reset our curString as empty string and curNum as 0 to use in further processing as we have a open bracket which means start of a new substring.
    • Finally when we encounter a close bracket ], it certainly means we have reached where our substring is complete, now we have to find a way to calculate it. That’s when we go back to stack to find what we have stored there which will help us in calculating the current substring. In the stack, we will find a number on top which is popped and then a previous string which we will need to add with the num*curString, and everything will be stored in curString after calculation.
    • The calculated curString will be returned as answer if s is over else it will be again appended to stack when an open bracket is encountered. And the above process will be repeated per condition.
class Solution(object):
    def decodeString(self, s: str) -> str:
        stack = []
        curNum = 0
        curString = ''
        
        for c in s:
            if c == '[':
                stack.append(curString)
                stack.append(curNum)
                curString = ''
                curNum = 0
            elif c == ']':
                num = stack.pop()
                prevString = stack.pop()
                curString = prevString + num*curString
            elif c.isdigit(): # curNum*10+int(c) is helpful in keep track of more than 1 digit number
                curNum = curNum*10 + int(c)
            else:
                curString += c
                
        return curString
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

[636/Medium] Exclusive Time of Functions

Problem

  • On a single-threaded CPU, we execute a program containing n functions. Each function has a unique ID between 0 and n-1.

  • Function calls are stored in a call stack: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is the current function being executed. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.

  • You are given a list logs, where logs[i] represents the i-th log message formatted as a string "{function_id}:{"start" | "end"}:{timestamp}". For example, "0:start:3" means a function call with function ID 0 started at the beginning of timestamp 3, and "1:end:2" means a function call with function ID 1 ended at the end of timestamp 2. Note that a function can be called multiple times, possibly recursively.

  • A function’s exclusive time is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for 2 time units and another call executing for 1 time unit, the exclusive time is 2 + 1 = 3.

  • Return the exclusive time of each function in an array, where the value at the i-th index represents the exclusive time for the function with ID i.

  • Example 1:

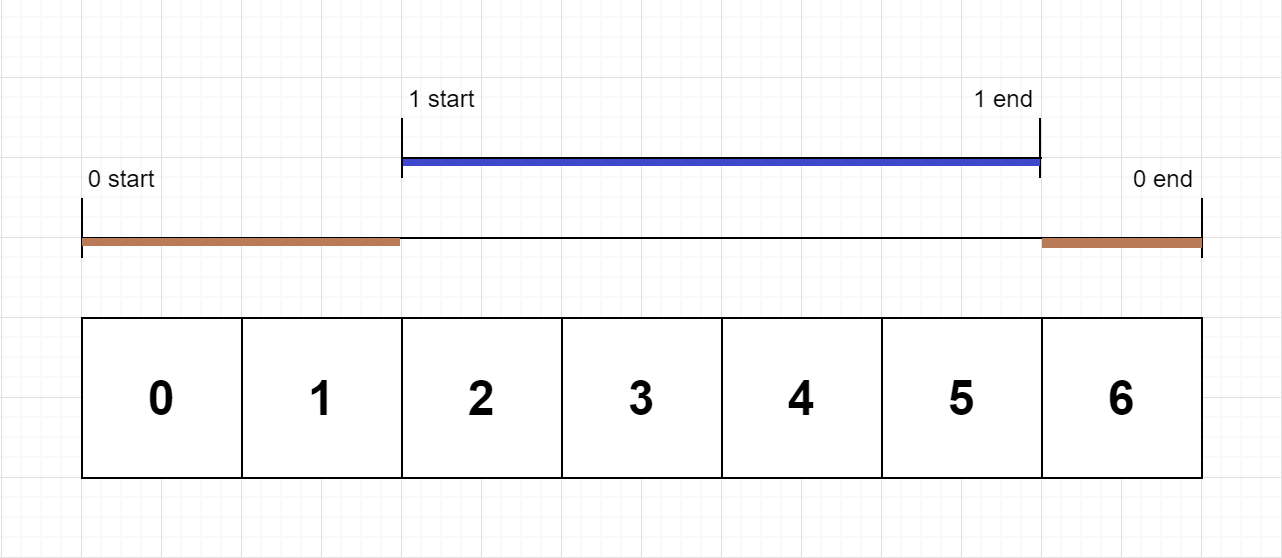
Input: n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]
Output: [3,4]
Explanation:
Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1.
Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5.
Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time.
So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
  • Example 2:
Input: n = 1, logs = ["0:start:0","0:start:2","0:end:5","0:start:6","0:end:6","0:end:7"]
Output: [8]
Explanation:
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls itself again.
Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time.
Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time.
So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
  • Example 3:
Input: n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:6","1:end:6","0:end:7"]
Output: [7,1]
Explanation:
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
  • Constraints:
    • 1 <= n <= 100
    • 1 <= logs.length <= 500
    • 0 <= function_id < n
    • 0 <= timestamp <= 109
    • No two start events will happen at the same timestamp.
    • No two end events will happen at the same timestamp.
    • Each function has an "end" log for each "start" log.
  • See problem on LeetCode.

Solution: Stack

class Solution:
    def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:
        stack = []
        result = [0] * n
        
        def normalizeProcessTime(processTime):
            return processTime.split(':') 
        
        for processTime in logs:
            processId, eventType, time = normalizeProcessTime(processTime)
            
            if eventType == "start":
                stack.append([processId, time])
            
            elif eventType == "end":
                processId, startTime = stack.pop()
                timeSpent = int(time) - int(startTime) + 1 # Add 1 cause 0 is included
                result[int(processId)] += timeSpent
                
                # Decrement time for next process in the stack
                if len(stack) != 0:
                    nextProcessId, timeSpentByNextProcess = stack[-1]
                    result[int(nextProcessId)] -= timeSpent
                    
        return result
  • Same approach; rehashed:
    • Split a function call to two different type of states:
      • Before nested call was made.
      • After nested call was made.
    • Record time spent on these two types of states
    • For e.g., for n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"].
      • Initially stack is empty, then it will record [[0, 0]] meaning function 0 start at timestamp 0.
      • Then nested call happens, we record time spent on function 0 in ans, then append to stack
        • Record time spent before nested call ans[s[-1][0]] += timestamp - s[-1][1].
      • Now stack has [[0, 0], [1, 2]].
      • When a end is met, pop top of stack and record time as timestamp - s.pop()[1] + 1.
      • Now stack is back to [[0, 0]], but before we end this iteration, we need to update the start time of this record.
        • Because time spent on it before nested call is recorded, so now it’s like a new start.
        • Update start time: s[-1][1] = timestamp+1
class Solution:
    def exclusiveTime(self, n: int, logs: List[str]) -> List[int]:
        # to covert id and time to integer
        helper = lambda log: (int(log[0]), log[1], int(log[2]))
        
        # convert ["0:start:0", ...] to [(0, start, 0)]
        logs = [helper(log.split(':')) for log in logs]         
        
        # initialize answer and stack
        ans, s = [0] * n, []
        
        # for each record
        for (i, status, timestamp) in logs:
            # if it's the start
            if status == 'start':
                # if s is not empty, update time spent on previous id (s[-1][0])
                if s: 
                    ans[s[-1][0]] += timestamp - s[-1][1]
                # then add to top of stack
                s.append([i, timestamp])
            # if it's the end
            else:
                # update time spend on `i`
                ans[i] += timestamp - s.pop()[1] + 1
                # if s is not empty, update start time of previous id
                if s: s[-1][1] = timestamp+1
                
        return ans
Complexity
  • Time: \(O(m)\) where where \(n\) is the number of logs (note that the length of each log is fixed and is thus a constant)
  • Space: \(O(n)\)

[921/Medium] Minimum Add to Make Parentheses Valid

Problem

  • A parentheses string is valid if and only if:
    • It is the empty string,
    • It can be written as AB (A concatenated with B), where A and B are valid strings, or
    • It can be written as (A), where A is a valid string.
  • You are given a parentheses string s. In one move, you can insert a parenthesis at any position of the string.
    • For example, if s = "()))", you can insert an opening parenthesis to be "(()))" or a closing parenthesis to be "())))".

  • Return the minimum number of moves required to make s valid.

  • Example 1:
Input: s = "())"
Output: 1
  • Example 2:
Input: s = "((("
Output: 3
  • Constraints:
    • 1 <= s.length <= 1000
    • s[i] is either '(' or ')'.

Solution: Two counts

class Solution:
    def without_stack(self, S):
        opening = count = 0
        for i in S:
            if i == '(': 
                opening += 1
            else:
                if opening: opening -= 1
                else: count += 1
        return count + opening
Complexity
  • Time: \(O(n)\)
  • Space: \(O(1)\)

Solution: Stack

class Solution:
    def using_stack(self, S):
        """
        :type S: str
        :rtype: int
        """
        stack = []
        
        for ch in S: # or traverse the string using "for i in range(len(S))" and access "S[i]"
            # if character is "(", then append to the stack
            if ch == '(': 
                stack.append(ch)
            else:
                # check if stack has a character and also if the character is "(", then pop the character
                if len(stack) and stack[-1] == '(': 
                    stack.pop()
                
                # else append ")" into the stack
                else: 
                    stack.append(ch)
                    
        # Return the length of the stack which indicates 
        # the number of invalid parenthesis
        return len(stack)
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

[1047/Easy] Remove All Adjacent Duplicates In String

Problem

  • You are given a string s consisting of lowercase English letters. A duplicate removal consists of choosing two adjacent and equal letters and removing them.

  • We repeatedly make duplicate removals on s until we no longer can.

  • Return the final string after all such duplicate removals have been made. It can be proven that the answer is unique.

  • Example 1:

Input: s = "abbaca"
Output: "ca"
Explanation: 
For example, in "abbaca" we could remove "bb" since the letters are adjacent and equal, and this is the only possible move.  The result of this move is that the string is "aaca", of which only "aa" is possible, so the final string is "ca".
  • Example 2:
Input: s = "azxxzy"
Output: "ay"
  • Constraints:
    • 1 <= s.length <= 105
    • s consists of lowercase English letters.
  • See problem on LeetCode.

Solution: Build stack and match last

class Solution:
    def removeDuplicates(self, s: str) -> str:
        stack = []
        
        for c in s:
            if stack and stack[-1] == c:
                stack.pop()
            else:
                stack.append(c)
        
        return ''.join(stack)
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

[1209/Medium] Remove All Adjacent Duplicates in String II

Problem

  • You are given a string s and an integer k, a k duplicate removal consists of choosing k adjacent and equal letters from s and removing them, causing the left and the right side of the deleted substring to concatenate together.

  • We repeatedly make k duplicate removals on s until we no longer can.

  • Return the final string after all such duplicate removals have been made. It is guaranteed that the answer is unique.

  • Example 1:

Input: s = "abcd", k = 2
Output: "abcd"
Explanation: There's nothing to delete.
  • Example 2:
Input: s = "deeedbbcccbdaa", k = 3
Output: "aa"
Explanation: 
First delete "eee" and "ccc", get "ddbbbdaa"
Then delete "bbb", get "dddaa"
Finally delete "ddd", get "aa"
  • Example 3:
Input: s = "pbbcggttciiippooaais", k = 2
Output: "ps"
  • Constraints:
    • 1 <= s.length <= 105
    • 2 <= k <= 104
    • s only contains lower case English letters.
  • See problem on LeetCode.

Solution: Recursion

class Solution:
    def removeDuplicates(self, s: str, k: int) -> str:
        count, i = 1, 1
        
        while i < len(s):
            if s[i] == s[i-1]: 
                count += 1
            else: 
                count = 1
            if count == k: 
                # skip k chars
                s = self.removeDuplicates(s[:i+1-k] + s[i+1:], k)
            i += 1
            
        return s
Complexity
  • Time: \(O(n)\)
  • Space: \(O(1)\)

Solution: One-liner

class Solution:
    def removeDuplicates(self, s: str, k: int) -> str:
        for letter in s:
            s = s.replace(letter * k, "")
            
        return s
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

Solution: Stack

  • Stack that tracks character and count, increment count in stack, pop when count reaches k.
class Solution:
    def removeDuplicates(self, s: str, k: int) -> str:
        stack = []
        res = ''
        
        for i in s:
            if not stack:
                # push character with length of adjacency = 1
                stack.append([i,1])
                continue
                
            if stack[-1][0] == i:
                # update last character's length of adjacency
                stack[-1][1] += 1
            else:
                # push character with length of adjacency = 1
                stack.append([i,1])
                
            if stack[-1][1] == k:
                # pop last character if it has repeated k times
                stack.pop()
                
        # generate output string                
        for i in stack:
            res += i[0] * i[1]
        
        return res
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

[1246/Medium] Minimum Remove to Make Valid Parentheses

Problem

  • Given a string s of ( , ) and lowercase English characters.
  • Your task is to remove the minimum number of parentheses (( or ), in any positions ) so that the resulting parentheses string is valid and return any valid string.
  • Formally, a parentheses string is valid if and only if:
    • It is the empty string, contains only lowercase characters, or
    • It can be written as AB (A concatenated with B), where A and B are valid strings, or
    • It can be written as (A), where A is a valid string.
  • Example 1:
Input: s = "lee(t(c)o)de)"
Output: "lee(t(c)o)de"
Explanation: "lee(t(co)de)" , "lee(t(c)ode)" would also be accepted.
  • Example 2:
Input: s = "a)b(c)d"
Output: "ab(c)d"
  • Example 3:
Input: s = "))(("
Output: ""
Explanation: An empty string is also valid.
  • Constraints:
    • 1 <= s.length <= 105
    • s[i] is either'(' , ')', or lowercase English letter.
  • See problem on LeetCode.

Solution: Stack

  1. Convert the input string to a list, because string is an immutable data structure in Python and it’s much easier and memory-efficient to deal with a list for this task.
  2. Iterate through the list.
  3. Keep track of indices with open parentheses in the stack. In other words, when we come across open parenthesis, we add an index to the stack.
  4. When we come across closed parenthesis, we pop an element from the stack. If the stack is empty we replace current list element with an empty string.
  5. After iteration, we replace all indices we have in the stack with empty strings, because we don’t have close parentheses for them.
  6. Convert list to string and return
def minRemoveToMakeValid(self, s: str) -> str:
    s = list(s)
    stack = []
    for i, char in enumerate(s):
        if char == '(':
            stack.append(i)
        elif char == ')':
            if stack:
                stack.pop()
            else:
                # Remove closed parentheses for which we don't have open parentheses.
                s[i] = ''
    
    # Remove invalid open parentheses for which we don't have close parentheses.
    while stack:             # or for i in stack:
        s[stack.pop()] = ''  #    s[i] = ''
        
    return ''.join(s)
Complexity
  • Time: \(O(3n) = O(n)\)
  • Space: \(O(n)\)