Distilled • LeetCode • Sliding/Rolling/Moving Window
- Pattern: Sliding/Rolling/Moving Window
- Introduction
- Approach: Brute Force
- Complexity
- Approach: Sliding Window
- [1/Easy] Two Sum
- [Easy] Maximum Sum Subarray of Size K
- [3/Medium] Longest Substring Without Repeating Characters
- [15/Medium] 3Sum
- [18/Medium] 4Sum
- [30/Hard] Substring with Concatenation of All Words
- [76/Hard] Minimum Window Substring
- [167/Medium] Two Sum II - Input Array Is Sorted
- [198/Medium] House Robber
- [904/Medium] Fruit Into Baskets
- [1291/Medium] Sequential Digits
Pattern: Sliding/Rolling/Moving Window
Introduction
-
In many problems dealing with an array (or a LinkedList), we are asked to find or calculate something among all the subarrays (or sublists) of a given size. For example, take a look at this problem:
-
Given an array, find the average of all subarrays of ‘K’ contiguous elements in it.
-
Let’s understand this problem with a real input:
Array: [1, 3, 2, 6, -1, 4, 1, 8, 2], K=5
- Here, we are asked to find the average of all subarrays of ‘5’ contiguous elements in the given array. Let’s solve this:
1. For the first 5 numbers (subarray from index 0-4), the average is: (1+3+2+6-1)/5 => 2.2(1+3+2+6−1)/5=>2.2
1. The average of next 5 numbers (subarray from index 1-5) is: (3+2+6-1+4)/5 => 2.8(3+2+6−1+4)/5=>2.8
1. For the next 5 numbers (subarray from index 2-6), the average is: (2+6-1+4+1)/5 => 2.4(2+6−1+4+1)/5=>2.4
...
- Here is the final output containing the averages of all subarrays of size 5:
Output: [2.2, 2.8, 2.4, 3.6, 2.8]
Approach: Brute Force
- A brute-force algorithm will calculate the sum of every 5-element subarray of the given array and divide the sum by ‘5’ to find the average. This is what the algorithm will look like:
def find_averages_of_subarrays(K, arr):
result = []
for i in range(len(arr)-K+1):
# find sum of next 'K' elements
_sum = 0.0
for j in range(i, i+K):
_sum += arr[j]
result.append(_sum/K) # calculate average
return result
def main():
result = find_averages_of_subarrays(5, [1, 3, 2, 6, -1, 4, 1, 8, 2])
print("Averages of subarrays of size K: " + str(result))
main()
Complexity
- Time:
-
Since for every element of the input array, we are calculating the sum of its next \(K\) elements, the time complexity of the above algorithm will be \(O(N*K)\) where \(N\) is the number of elements in the input array.
-
Can we find a better solution? Do you see any inefficiency in the above approach?
-
The inefficiency is that for any two consecutive subarrays of size ‘5’, the overlapping part (which will contain four elements) will be evaluated twice. For example, take the above-mentioned input:
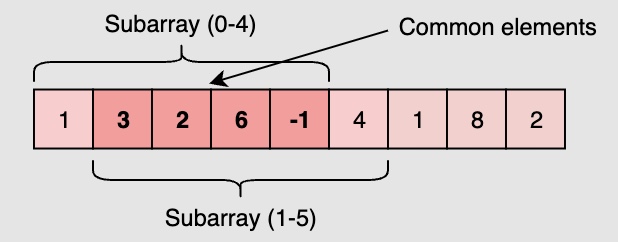
-
As you can see, there are four overlapping elements between the subarray (indexed from 0-4) and the subarray (indexed from 1-5). Can we somehow reuse the
sumwe have calculated for the overlapping elements? -
The efficient way to solve this problem would be to visualize each subarray as a rolling/sliding window of ‘5’ elements. This means that we will slide the window by one element when we move on to the next subarray. To reuse the
sumfrom the previous subarray, we will subtract the element going out of the window and add the element now being included in the sliding window. This will save us from going through the whole subarray to find thesumand, as a result, the algorithm complexity will reduce to \(O(N)\).
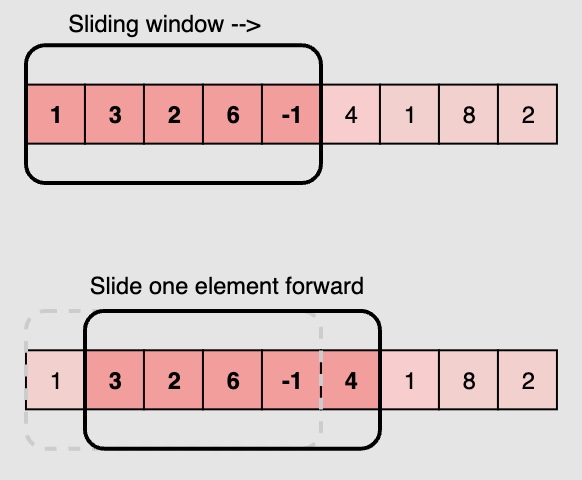
-
Approach: Sliding Window
def find_averages_of_subarrays(K, arr):
result = []
windowSum, windowStart = 0.0, 0
for windowEnd in range(len(arr)):
windowSum += arr[windowEnd] # add the next element
# slide the window, we don't need to slide if we've not hit the required window size of 'k'
if windowEnd >= K - 1:
print(windowEnd, K)
result.append(windowSum / K) # calculate the average
windowSum -= arr[windowStart] # subtract the element going out
windowStart += 1 # slide the window ahead
return result
def main():
result = find_averages_of_subarrays(5, [1, 3, 2, 6, -1, 4, 1, 8, 2])
print("Averages of subarrays of size K: " + str(result))
main()
- Note that in some problems, the size of the sliding window is not fixed. We have to expand or shrink the window based on the problem constraints.
[1/Easy] Two Sum
- In general, sum problems can be categorized into two categories:
- There is an array and you add some numbers to get to (or close to) a target, or
- You need to return indices of numbers that sum up to a (or close to) a target value.
- Note that when the problem is looking for a indices, sorting the array is probably NOT a good idea.
Problem
- Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.
- You may assume that each input would have exactly one solution, and you may not use the same element twice.
-
You can return the answer in any order.
- Example 1:
Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].
- Example 2:
Input: nums = [3,2,4], target = 6
Output: [1,2]
- Example 3:
Input: nums = [3,3], target = 6
Output: [0,1]
- Constraints:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- Only one valid answer exists.
- See problem on LeetCode.
Solution: Sliding Window
- This is the second type of the problems where we’re looking for indices, so sorting is not necessary. What you’d want to do is to go over the array, and try to find two integers that sum up to a target value. Most of the times, in such a problem, using dictionary (hastable) helps. You try to keep track of you’ve observations in a dictionary and use it once you get to the results.
- In this problem, you initialize a dictionary (
seen). This dictionary will keep track of numbers (askey) and indices (asvalue). - So, you go over your array (line #1) using
enumeratethat gives you both index and value of elements in array. - As an example, let’s do
nums = [2,3,1]andtarget = 3. Let’s say you’re at indexi = 0andvalue = 2, ok? you need to findvalue = 1to finish the problem, meaning,target - 2 = 1. 1 here is the remaining. Since remaining + value = target, you’re done once you found it. - So when going through the array, you calculate the remaining and check to see whether remaining is in the seen dictionary (line #3). If it is, you’re done!
- The current number and the remaining from
seenwould give you the output (line #4). - Otherwise, you add your current number to the dictionary (line #5) since it’s going to be a remaining for (probably) a number you’ll see in the future assuming that there is at least one instance of answer.
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
seen = {}
for i, value in enumerate(nums): #1
remaining = target - nums[i] #2
if remaining in seen: #3
return [i, seen[remaining]] #4
else:
seen[value] = i #5
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[Easy] Maximum Sum Subarray of Size K
Problem
-
Given an array of positive numbers and a positive number ‘k,’ find the maximum sum of any contiguous subarray of size ‘k’.
-
Example 1:
Input: [2, 1, 5, 1, 3, 2], k=3
Output: 9
Explanation: Subarray with maximum sum is [5, 1, 3].
- Example 2:
Input: [2, 3, 4, 1, 5], k=2
Output: 7
Explanation: Subarray with maximum sum is [3, 4].
Solution: Brute force
- A basic brute force solution will be to calculate the sum of all ‘k’ sized subarrays of the given array to find the subarray with the highest sum. We can start from every index of the given array and add the next ‘k’ elements to find the subarray’s sum. Following is the visual representation of this algorithm for example 1:
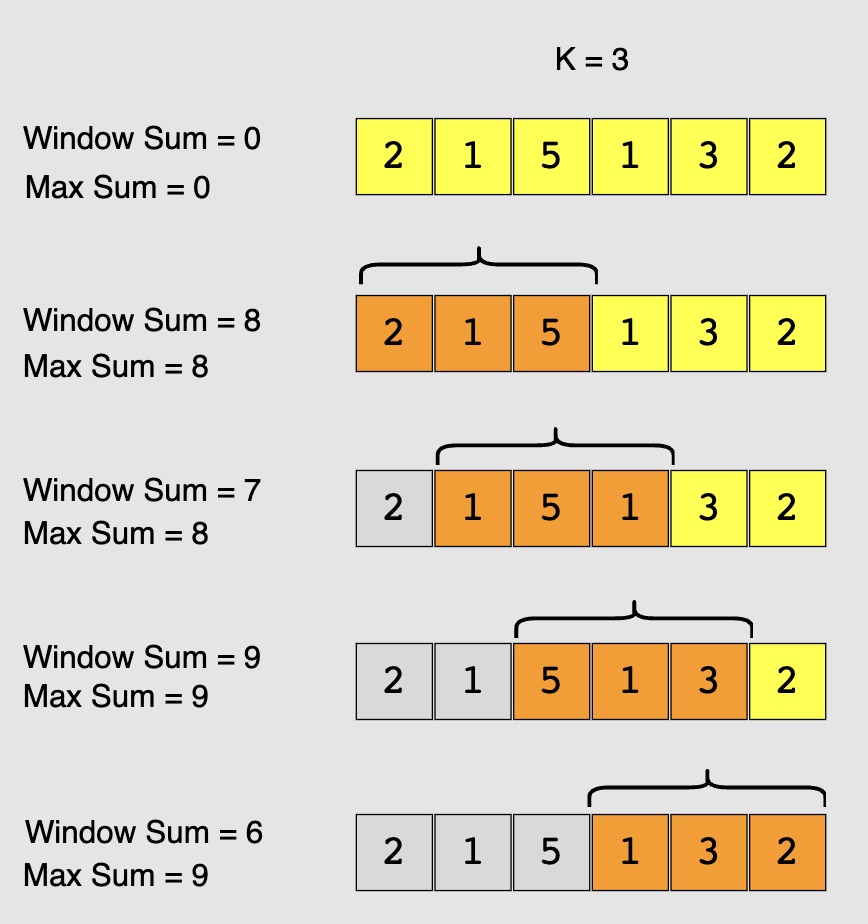
def max_sub_array_of_size_k(k, arr):
max_sum = 0
window_sum = 0
for i in range(len(arr) - k + 1):
window_sum = 0
for j in range(i, i+k):
window_sum += arr[j]
max_sum = max(max_sum, window_sum)
return max_sum
def main():
print("Maximum sum of a subarray of size K: " + str(max_sub_array_of_size_k(3, [2, 1, 5, 1, 3, 2])))
print("Maximum sum of a subarray of size K: " + str(max_sub_array_of_size_k(2, [2, 3, 4, 1, 5])))
main()
Complexity
- Time: \(O(N*K)\), where ‘N’ is the total number of elements in the given array.
Solution: Sliding window
- If you observe closely, you will realize that to calculate the sum of a contiguous subarray, we can utilize the sum of the previous subarray. For this, consider each subarray as a Sliding Window of size ‘k.’ To calculate the sum of the next subarray, we need to slide the window ahead by one element. So to slide the window forward and calculate the sum of the new position of the sliding window, we need to do two things:
- Subtract the element going out of the sliding window, i.e., subtract the first element of the window.
- Add the new element getting included in the sliding window, i.e., the element coming right after the end of the window.
- This approach will save us from re-calculating the sum of the overlapping part of the sliding window. Here is what our algorithm will look like:
def max_sub_array_of_size_k(k, arr):
max_sum , window_sum = 0, 0
window_start = 0
for window_end in range(len(arr)):
window_sum += arr[window_end] # add the next element
# slide the window, we don't need to slide if we've not hit the required window size of 'k'
if window_end >= k-1:
max_sum = max(max_sum, window_sum)
window_sum -= arr[window_start] # subtract the element going out
window_start += 1 # slide the window ahead
return max_sum
def main():
print("Maximum sum of a subarray of size K: " + str(max_sub_array_of_size_k(3, [2, 1, 5, 1, 3, 2])))
print("Maximum sum of a subarray of size K: " + str(max_sub_array_of_size_k(2, [2, 3, 4, 1, 5])))
main()
Complexity
- Time: \(O(N)\)
- Space: \(O(1)\)
[3/Medium] Longest Substring Without Repeating Characters
Problem
-
Given a string
s, find the length of the longest substring without repeating characters. -
Example 1:
Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.
- Example 2:
Input: s = "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.
- Example 3:
Input: s = "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.
- Constraints:
0 <= s.length <= 5 * 104s consists of English letters, digits, symbols and spaces.
Solution: Brute Force
- Intuition:
- Check all the substring one by one to see if it has no duplicate character.
- Algorithm:
- Suppose we have a function
boolean allUnique(String substring)which will return true if the characters in the substring are all unique, otherwise false. We can iterate through all the possible substrings of the given string s and call the functionallUnique. If it turns out to be true, then we update our answer of the maximum length of substring without duplicate characters. - Now let’s fill the missing parts:
- To enumerate all substrings of a given string, we enumerate the start and end indices of them. Suppose the start and end indices are \(i\) and \(j\), respectively. Then we have \(0 \leq i \lt j \leq n\) (here end index \(j\) is exclusive by convention). Thus, using two nested loops with \(i\) from \(0\) to \(n - 1\) and \(j\) from \(i+1\) to \(n\), we can enumerate all the substrings of \(s\).
- To check if one string has duplicate characters, we can use a set. We iterate through all the characters in the string and put them into the set one by one. Before putting one character, we check if the set already contains it. If so, we return
false. After the loop, we returntrue.
- Suppose we have a function
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
def check(start, end):
chars = [0] * 128
for i in range(start, end + 1):
c = s[i]
chars[ord(c)] += 1
if chars[ord(c)] > 1:
return False
return True
n = len(s)
res = 0
for i in range(n):
for j in range(i, n):
if check(i, j):
res = max(res, j - i + 1)
return res
Complexity
- Time: \(O(n^3)\)
- Space: \(O(min(n,m))\). We need \(O(k)\) space for checking a substring has no duplicate characters, where \(k\) is the size of the
Set. The size of the Set is upper bounded by the size of the string \(n\) and the size of the charset/alphabet \(m\).
Solution: Sliding Window
- Algorithm:
- The naive approach is very straightforward. But it is too slow. So how can we optimize it?
- In the naive approaches, we repeatedly check a substring to see if it has duplicate character. But it is unnecessary. If a substring \(s_{ij}\) from index \(i\) to \(j - 1\) is already checked to have no duplicate characters. We only need to check if \(s[j]\) is already in the substring \(s_{ij}\).
- To check if a character is already in the substring, we can scan the substring, which leads to an \(O(n^2)\) algorithm. But we can do better.
- By using HashSet as a sliding window, checking if a character in the current can be done in \(O(1)\).
- A sliding window is an abstract concept commonly used in array/string problems. A window is a range of elements in the array/string which usually defined by the start and end indices, i.e., \([i, j)\) (left-closed, right-open). A sliding window is a window “slides” its two boundaries to the certain direction. For example, if we slide \([i, j)\) to the right by 1 element, then it becomes \([i+1, j+1)\) (left-closed, right-open).
- Back to our problem. We use HashSet to store the characters in current window \([i, j)\) (\(j = i\) initially). Then we slide the index \(j\) to the right. If it is not in the HashSet, we slide \(j\) further. Doing so until \(s[j]\) is already in the HashSet. At this point, we found the maximum size of substrings without duplicate characters start with index \(i\). If we do this for all \(i\), we get our answer.
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
chars = [0] * 128
left = right = 0
res = 0
while right < len(s):
r = s[right]
chars[ord(r)] += 1
# loop until
while chars[ord(r)] > 1:
l = s[left]
chars[ord(l)] -= 1
left += 1
res = max(res, right - left + 1)
right += 1
return res
Complexity
- Time: \(O(2n) = O(n)\). In the worst case each character will be visited twice by ii and jj.
- Space: \(O(min(n,m))\). We need \(O(k)\) space for the sliding window, where \(k\) is the size of the
Set. The size of the Set is upper bounded by the size of the string nn and the size of the charset/alphabet \(m\).
Solution: Sliding Window with Hashmap
- The above solution requires at most \(2n\) steps. In fact, it could be optimized to require only n steps. Instead of using a set to tell if a character exists or not, we could define a mapping of the characters to its index. Then we can skip the characters immediately when we found a repeated character.
- The reason is that if \(s[j]\) have a duplicate in the range \([i, j)\) with index \(j'\), we don’t need to increase \(i\) little by little. We can skip all the elements in the range \([i, j']\) and let \(i\) to be \(j' + 1\) directly.
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
n = len(s)
ans = 0
# charMapping stores the mapping of the "current" index of a character
charMapping = {}
i = 0
# try to extend the range [i, j]
for j in range(n):
if s[j] in charMapping:
i = max(charMapping[s[j]], i)
ans = max(ans, j - i + 1)
charMapping[s[j]] = j + 1
return ans
Complexity
- Time: \(O(n)\). Index \(j\) will iterate \(n\) times.
- Space: \(O(min(m,n))\). Same as the previous approach.
Sliding Window with an Integer Array
- The previous implementations all have no assumption on the charset of the string
s. - If we know that the charset is rather small, we can replace the Map with an integer array as direct access table.
- Commonly used tables are:
int[26]for Letters ‘a’ - ‘z’ or ‘A’ - ‘Z’int[128]for ASCIIint[256]for Extended ASCII
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
n = len(s)
ans = 0
# charMapping stores the mapping of the "current" index of a character
charMapping = [None] * 128
i = 0
# try to extend the range [i, j]
for j in range(n):
if charMapping[ord(s[j])] is not None:
i = max(charMapping[ord(s[j])], i)
ans = max(ans, j - i + 1)
charMapping[ord(s[j])] = j + 1
return ans
- Same approach, rephrased:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
chars = [None] * 128
left = right = 0
res = 0
while right < len(s):
r = s[right]
index = chars[ord(r)]
if index != None and index >= left and index < right:
left = index + 1
res = max(res, right - left + 1)
chars[ord(r)] = right
right += 1
return res
Complexity
- Time: \(O(n)\). Index \(j\) will iterate \(n\) times.
- Space: \(O(m)\), where \(m\) is the size of the charset.
[15/Medium] 3Sum
Problem
- Given an integer array
nums, return all the triplets[nums[i], nums[j], nums[k]]such thati != j,i != k, andj != k, andnums[i] + nums[j] + nums[k]== 0. -
Notice that the solution set must not contain duplicate triplets.
- Example 1:
Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]
- Example 2:
Input: nums = []
Output: []
- Example 3:
Input: nums = [0]
Output: []
- Constraints:
0 <= nums.length <= 3000-105 <= nums[i] <= 105
- See problem on LeetCode.
Solution: Adapt to Two-Sum
- Another way to solve this problem is to change it into a two sum problem. Instead of finding
a+b+c = 0, you can finda+b = -cwhere we want to find two numbersaandbthat are equal to-c. This is similar to the first problem. Remember if you wanted to use the exact same as the first code, it’d return indices and not numbers. Also, we need to re-arrange this problem in a way that we havenumsandtarget.
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res = []
nums.sort()
for i in range(len(nums)-2):
if i > 0 and nums[i] == nums[i-1]:
continue
output_2sum = self.twoSum(nums[i+1:], -nums[i])
if output_2sum ==[]:
continue
else:
for idx in output_2sum:
instance = idx + [nums[i]]
res.append(instance)
output = []
for idx in res:
if idx not in output:
output.append(idx)
return output
def twoSum(self, numbers: List[int], target: int) -> List[int]:
seen = {}
res = []
for i, value in enumerate(nums): #1
remaining = target - nums[i] #2
if remaining in seen: #3
res.append([value, remaining]) #4
else:
seen[value] = i #5
return res
Complexity
- Time: \(O(n^2)\)
- Space: \(O(n)\)
Solution: Two pointers
-
This is similar to the Two Sum II - Input Array is Sorted problem except that it’s looking for three numbers. There are some minor differences in the problem statement. It’s looking for all combinations (not just one) of solutions returned as a list. And second, it’s looking for unique combinations, so repetition is not allowed.
-
Here, instead of looping (line #1) to
len(nums) - 1, we loop tolen(nums) - 2since we’re looking for three numbers. Since we’re returning values, sort would be a good idea. Otherwise, if thenumsis not sorted, you cannot reducingrightpointer or increasingleftpointer easily. -
So, first you
sortthe array and defineres = []to collect your outputs. In line #2, we check whether two consecutive elements are equal or not because if they are, we don’t want them (solutions need to be unique) and will skip to the next set of numbers. Also, there is an additional constrain in this line thati > 0. This is added to take care of cases likenums = [1, 1, 1]andtarget = 3. If we didn’t havei > 0, then we’d skip the only correct solution and would return[]as our answer which is wrong (correct answer is[[1, 1, 1]]. -
We define two additional pointers this time,
left = i + 1andright = len(nums) - 1. For example, if nums =[-2, -1, 0, 1, 2], all the points in the case of i=1 are looking at:iat -1, left at 0 and right at 2. We then check temp variable similar to the previous example. There is only one change with respect to the previous example here between lines #5 and #10. If we have thetemp = target, we obviously add this set toresin line #5. However, we’re not done yet. For a fixedi, we still need to check and see whether there are other combinations by just changing left and right pointers. That’s what we are doing in lines #6, 7, 8. If we still have the condition ofleft < rightandnums[left]and the number to the right of it are not the same, we move left one index to right (line #6). Similarly, ifnums[right]and the value to left of it is not the same, we move right one index to left. This way for a fixed i, we get rid of repetitive cases. For example, ifnums = [-3, 1, 1, 3,5]andtarget = 3, one we get the first[-3, 1, 5],left = 1, but,nums[2]is also 1 which we don’t want the left variable to look at it simply because it’d again return[-3, 1, 5]. So, we move left one index. Finally, if the repeating elements don’t exists, lines #6 to #8 won’t get activated. In this case we still need to move forward by adding 1 to left and extracting 1 from right (lines #9, 10).
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort() # We need to sort the list first!
res = [] # Result list holding the triplets
# len(nums)-2 is because we need at least 3 numbers to continue.
for i in range(len(nums)-2): #1
# Since the list is sorted, if nums[i] > 0, then all
# nums[j] with j > i are positive as well, and we cannot
# have three positive numbers sum up to 0. Return immediately.
if nums[i] > 0:
break
# if i > 0 is because when i = 0, it doesn't need to check if it's a duplicate
# element since it doesn't even have a previous element to compare with.
# This condition also helps avoid a negative index, i.e., when i = 0, nums[i-1] = nums[-1]
# and you don't want to skip this iteration when nums[0] == nums[-1]
# The nums[i] == nums[i-1] condition helps us avoid duplicates.
# E.g., given [-1, -1, 0, 0, 1], when i = 0, we see [-1, 0, 1]
# works. Now at i = 1, since nums[1] == -1 == nums[0], we avoid
# this iteration and thus avoid duplicates.
if i > 0 and nums[i] == nums[i-1]: #2
continue
# Classic two pointer solution
left = i + 1 #3
right = len(nums) - 1 #4
while left < right:
curr_sum = nums[i] + nums[left] + nums[right]
if curr_sum > 0: # sum too large, move right ptr
right -= 1
elif curr_sum < 0: # sum too small, move left ptr
left += 1
else:
res.append([nums[i], nums[left], nums[right]]) #5
# the below 2 loops are to avoid duplicate triplets
# we need to skip elements that are identical to our
# current solution, otherwise we would have duplicated triples
while left < right and nums[left] == nums[left + 1]: #6
left += 1
while left < right and nums[right] == nums[right - 1]:#7
right -= 1 #8
right -= 1 #9
left += 1 #10
return res
Complexity
- Time: \(O(n^2)\)
- Space: \(O(n)\)
[18/Medium] 4Sum
Problem
- Given an array
numsofnintegers, return an array of all the unique quadruplets[nums[a], nums[b], nums[c], nums[d]]such that:0 <= a, b, c, d < na, b, c, and d are distinct.nums[a] + nums[b] + nums[c] + nums[d] == target
-
You may return the answer in any order.
- Example 1:
Input: nums = [1,0,-1,0,-2,2], target = 0
Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
- Example 2:
Input: nums = [2,2,2,2,2], target = 8
Output: [[2,2,2,2]]
- Constraints:
1 <= nums.length <= 200-109 <= nums[i] <= 109-109 <= target <= 109
- See problem on LeetCode.
Solution: Two pointers
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
# Sort the initial list
nums.sort()
# HashMap for the solution, to avoid duplicates
solution = {}
# i = 0 ..... n-1
for i in range(len(nums)):
#j = i+1 ..... n-1
for j in range(i+1, len(nums)):
# Two pointer approach to find the remaining two elements
start = j+1
end = len(nums) - 1
while start < end:
temp = nums[i] + nums[j] + nums[start] + nums[end]
if (temp == target):
solution[(nums[i], nums[j], nums[start], nums[end])] = True
start +=1
end -=1
elif temp < target:
start += 1
else:
end -=1
return solution.keys()
Complexity
- Time: \(O(n^3)\)
- Space: \(O(n)\)
Solution: Adapt to Two-Sum-II
-
You should have gotten the idea, and what you’ve seen so far can be generalized to nSum. Here, I write the generic code using the same ideas as before. What I’ll do is to break down each case to a 2Sum II problem, and solve them recursively using the approach in 2Sum II example above.
-
First sort nums, then I’m using two extra functions, helper and twoSum. The twoSum is similar to the 2sum II example with some modifications. It doesn’t return the first instance of results, it check every possible combinations and return all of them now. Basically, now it’s more similar to the 3Sum solution. Understanding this function shouldn’t be difficult as it’s very similar to 3Sum. As for helper function, it first tries to check for cases that don’t work (line #1). And later, if the N we need to sum to get to a target is 2 (line #2), then runs the twoSum function. For the more than two numbers, it recursively breaks them down to two sum (line #3). There are some cases like line #4 that we don’t need to proceed with the algorithm anymore and we can break. These cases include if multiplying the lowest number in the list by N is more than target. Since its sorted array, if this happens, we can’t find any result. Also, if the largest array (nums[-1]) multiplied by N would be less than target, we can’t find any solution. So, break.
-
For other cases, we run the helper function again with new inputs, and we keep doing it until we get to N=2 in which we use twoSum function, and add the results to get the final output.
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
nums.sort()
results = []
self.helper(nums, target, 4, [], results)
return results
def helper(self, nums, target, N, res, results):
if len(nums) < N or N < 2: #1
return
if N == 2: #2
output_2sum = self.twoSum(nums, target)
if output_2sum != []:
for idx in output_2sum:
results.append(res + idx)
else:
for i in range(len(nums) -N +1): #3
if nums[i]*N > target or nums[-1]*N < target: #4
break
if i == 0 or i > 0 and nums[i-1] != nums[i]: #5
self.helper(nums[i+1:], target-nums[i], N-1, res + [nums[i]], results)
def twoSum(self, nums: List[int], target: int) -> List[int]:
res = []
left = 0
right = len(nums) - 1
while left < right:
temp_sum = nums[left] + nums[right]
if temp_sum == target:
res.append([nums[left], nums[right]])
right -= 1
left += 1
while left < right and nums[left] == nums[left - 1]:
left += 1
while right > left and nums[right] == nums[right + 1]:
right -= 1
elif temp_sum < target:
left +=1
else:
right -= 1
return res
Complexity
- Time: TODO
- Space: TODO
[30/Hard] Substring with Concatenation of All Words
Problem
-
You are given a string
sand an array of stringswordsof the same length. Return all starting indices ofsubstring(s)insthat is a concatenation of each word inwordsexactly once, in any order, and without any intervening characters. -
You can return the answer in any order.
-
Example 1:
Input: s = "barfoothefoobarman", words = ["foo","bar"]
Output: [0,9]
Explanation: Substrings starting at index 0 and 9 are "barfoo" and "foobar" respectively.
The output order does not matter, returning [9,0] is fine too.
- Example 2:
Input: s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
Output: []
- Example 3:
Input: s = "barfoofoobarthefoobarman", words = ["bar","foo","the"]
Output: [6,9,12]
- Constraints:
1 <= s.length <= 104s consists of lower-case English letters.1 <= words.length <= 50001 <= words[i].length <= 30words[i] consists of lower-case English letters.
- See problem on LeetCode.
Solution: Approach 1: Check All Indices Using a Hash Table
- Intuition:
Definition: a valid substring is a string that is a concatenation of all of the words in our word bank. So if we are given the words “foo” and “bar”, then “foobar” and “barfoo” would be valid substrings.
- An important detail in the problem description to notice is that all elements in words have the same length. This gives us valuable information about all valid substrings - we know what length they will be. Each valid substring is the concatenation of words.length words which all have the same length, so each valid substring has a length of
words.length * words[0].length.

-
This makes it easy for us to take a given index and check if a valid substring starting at this index exists. Let’s say that the elements of words have a length of 3. Then, for a given starting index, we can just look at the string in groups of 3 characters and check if those characters form a word in words. Because words can have duplicate words, we should use a hash table to maintain a count for each word. As a bonus, a hash table also lets us search for word matches very quickly.
-
We can write a helper function that takes an index and returns if a valid substring starting at this index exists. Then, we can build our answer by running this function for all candidate indices. The logic for this function can be something along the lines of:
- Iterate from the starting index to the starting index plus the size of a valid substring.
- Iterate words[0].length characters at a time. At each iteration, we will look at a substring with the same length as the elements in words.
- If the substring doesn’t exist in words, or it does exist but we already found the necessary amount of it, then return false.
- We can use a hash table to keep an updated count of the words between the starting index and the current index.

- Algorithm:
- Initialize some variables:
nas the length ofs.kas the length of wordswordLengthas the length of each word in words.substringSizeaswordLength * k, which represents the size of each valid substring.wordCountas a hash table that tracks how many times a word occurs inwords.
- Create a function
checkthat takes a starting indexiand returns if a valid substring starts at indexi:- Create a copy of
wordCountto make use of for this particular index. Let’s call itremaining. Also, initialize an integer wordsUsed which tracks how many matches we have found so far. - Iterate starting from
i. Iterate untili + substringSize- we know that each valid substring will have this size, so we don’t need to go further. At each iteration, we will be checking for a word - and we know each word has a length of wordLength, so increment bywordLengtheach time. - If the variable we are iterating with is
j, then at each iteration, check for a wordsub = s.substring(j, j + wordLength). - If sub is in
remainingand has a value greater than 0, then decrease its count by 1 and increasewordsUsedby 1. Otherwise, break out of the loop. - At the end of it all, if
wordsUsed == k, that means we used up all the words in words and have found a valid substring. Return true if so, false otherwise.
- Create a copy of
- Now that we have this function check, we can just check all possible starting indices. Because a valid substring has a length of substringSize, we only need to iterate up to n -
substringSize. Build an array with all indices that pass check and return it.
- Initialize some variables:
- Implementation:
class Solution:
def findSubstring(self, s: str, words: List[str]) -> List[int]:
n = len(s)
k = len(words)
word_length = len(words[0])
substring_size = word_length * k
word_count = collections.Counter(words)
def check(i):
# Copy the original dictionary to use for this index
remaining = word_count.copy()
words_used = 0
# Each iteration will check for a match in words
for j in range(i, i + substring_size, word_length):
sub = s[j : j + word_length]
if remaining[sub] > 0:
remaining[sub] -= 1
words_used += 1
else:
break
# Valid if we used all the words
return words_used == k
answer = []
for i in range(n - substring_size + 1):
if check(i):
answer.append(i)
return answer
Complexity
- Time: \(O(n \cdot a \cdot b - (a \cdot b) ^ 2)\), given \(n\) as the length of \(s\), \(a\) as the length of words, and \(b\) as the length of each word.
- First, let’s analyze the time complexity of check. We start by creating a copy of our hash table, which in the worst case will take O(a)O(a) time, when words only has unique elements. Then, we iterate aa times (from i to i + substringSize, wordLength at a time): \(\text{substringSize / wordLength = words.length = a}\). At each iteration, we create a substring, which takes wordLength = bb time. Then we do a hash table check.
- That means each call to check uses O(a + a \cdot (b + 1))O(a+a⋅(b+1)) time, simplified to \(O(a \cdot b)\). How many times do we call check? Only \(n - substringSize\) times. Recall that substringSize is equal to the length of words times the length of words[0], which we have defined as aa and bb respectively here. That means we call check \(n - a \cdot b\) times.
- This gives us a time complexity of O((n - a \cdot b) \cdot a \cdot b)O((n−a⋅b)⋅a⋅b), which can be expanded to \(O(n \cdot a \cdot b - (a \cdot b) ^ 2)\).
- Space: \(O(a + b)\).
- Most of the time, the majority of extra memory we use is the hash table to store word counts. In the worst-case scenario where words only has unique elements, we will store up to aa keys.
- We also store substrings in sub which requires \(O(b)\) space. So the total space complexity of this approach is \(O(a + b)\). However, because for this particular problem the upper bound for \(b\) is very small (30), we can consider the space complexity to be \(O(a)\).
Solution: Sliding Window
- Intuition:
- In the previous approach, we made use of the fact that all elements of words share the same length, which allows us to efficiently check for valid substrings. Unfortunately, we repeated a lot of computation - each character of s is iterated over many times. Imagine if we had an input like this:
s = "barfoobarfoo" and words = ["bar", "foo"]
- Valid substrings start at index 0, 3, and 6. Notice that the substrings starting at indices 0 and 3 share the same “foo”. That means we are iterating over and handling this “foo” twice, which shouldn’t be necessary. We do it again with the substrings starting at indices 3 and 6 - they use the same “bar”. In this specific example it may not seem too bad, but imagine if we had an input like:
s = "aaaa...aaa", s.length = 10,000 and words = ["a", "a", ..., "a", "a"], words.length = 5000-
We would be iterating over the same characters millions of times. How can we avoid repeated computation? Let’s make use of a sliding window. We can re-use most of the logic from the previous approach, but this time instead of only checking for one valid substring at a time with each call to check, we will try to find all valid substrings in one pass by sliding our window across s.
-
So how will the left and right bounds of the window move, and how can we tell if we our window is a valid substring? Let’s say we start at index 0 and do the same process as the previous approach - iterate wordLength at a time, so that at each iteration we are focusing on one potential word. Our iteration variable, say right, can be our right bound. We can initialize our left bound at
0, sayleft = 0. -
Now, right will move at each iteration, by wordLength each time. At each iteration, we have a word sub = s.substring(right, right + wordLength). If sub is not in words, we know that we cannot possibly form a valid substring, so we should reset the entire window and try again, starting with the next iteration. If sub is in words, then we need to keep track of it. Like in the previous approach, we can use a hash table to keep count of all the words in our current window.


-
When our window has reached the maximum size (
substringSize), we can check if it is a valid substring. Like in the previous approach, we can use an integer wordsUsed to check ifwordsUsed == words.lengthto see if we made use of all the elements in words, and thus have a valid substring. If we do, then we can addleftto our answer. -
Whether we have a valid substring or not, if our window has reached maximum size, we need to move the left bound. This means we need to find the word we are removing from the window, and perform the necessary logic to keep our hash table up to date.
-
Another thing to note: we may encounter excess words. For example, with
s = "foofoobar", andwords = ["foo", "bar"], the two “foo” should not be matched together to havewordsUsed = 2. Whenever we find that sub is in words, we should check how many times we have seen sub so far in the current window (using our hash table), and if it is greater than the number of times it appears inwords(which we can find with a second hash table, wordCount in the first approach), then we know we have an excess word and should not incrementwordsUsed. -
In fact, so long as we have an excess word, we can never have a valid substring. Therefore, another criterion for moving our left bound should be to remove words from the left until we find the excess word and remove it (which we can accomplish by comparing the hash table values).

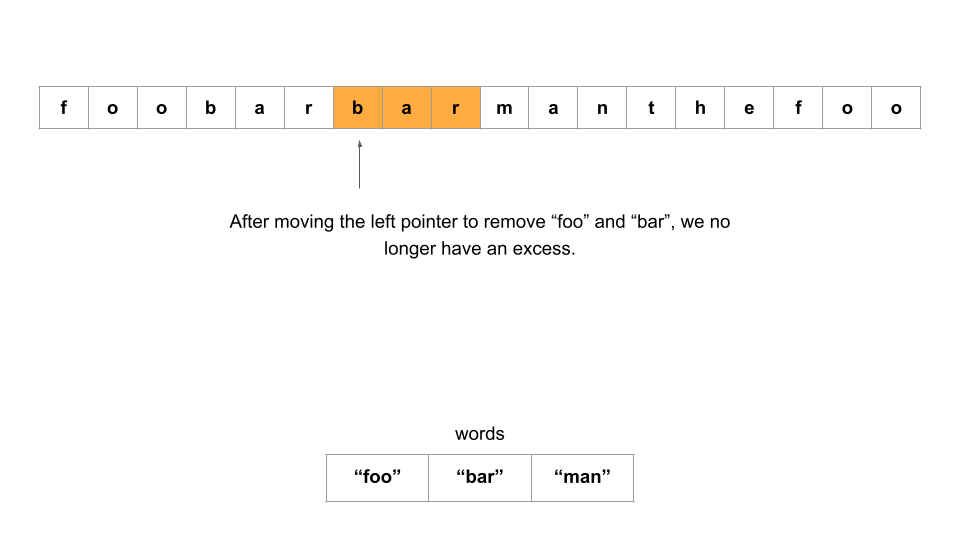
- Now that we’ve described the logic needed for the sliding window, how will we apply the window? In the first approach, we tried every candidate index (all indices up until n - substringSize). In this problem, you may notice that starting the process from two indices that are wordLength apart is pointless. For example, if we have
words = ["foo", "bar"], then starting from index 3 is pointless since by starting at index 0, we will move over index 3. However, we will still need to try starting from indices 1 and 2, in case the input looks something likes = "xfoobar"ors = "xyfoobar". As such, we will only need to perform the sliding windowwordLengthamount of times.

- Algorithm:
- Initialize some variables:
nas the length ofs.kas the length ofwords.wordLengthas the length of each word inwords.substringSizeaswordLength * k, which represents the size of each valid substring.wordCountas a hash table that tracks how many times a word occurs inwords.answeras an array that will hold the starting index of every valid substring.
- Create a function
slidingWindowthat takes an index left and starts a sliding window from left:- Initialize a hash table
wordsFoundthat will keep track of how many times a word appears in our window. Also, an integerwordsUsed = 0to keep track of how many words are in our window, and a booleanexcessWord = falsethat indicates if our window is currently holding an excess word, such as a third “foo” ifwords = ["foo", "foo"]. - Iterate using the right bound of our window, right. Start iteration at
left, untiln, wordLength at a time. At each iteration:- We are dealing with a word
sub = s.substring(right, right + wordLength). If sub is not inwordCount, then we must reset the window. Clear our hash table wordsFound, and reset our variableswordsUsed = 0andexcessWord = false. Move left to the next index we will handle, which will beright + wordLength. - Otherwise, if sub is in
wordCount, we can continue with our window. First, check if our window is beyond max size or has an excess word. So long as either of these conditions are true, move left over while appropriately updating our hash table, integer and boolean variables. - Now, we can handle
sub. Increment its value inwordsFound, and then compare its value in wordsFound to its value inwordCount. If the value is less than or equal, then we can make use of this word in a validsubstring - incrementwordsUsed. Otherwise, it is an excess word, and we should setexcessWord = true. - At the end of it all, if we have
wordsUsed == kwithout any excess words, then we have a valid substring. Add left to answer.
- We are dealing with a word
- Initialize a hash table
- Call
slidingWindowwith each index from 0 towordLength. Return answer once finished.
- Initialize some variables:
class Solution:
def findSubstring(self, s: str, words: List[str]) -> List[int]:
n = len(s)
k = len(words)
word_length = len(words[0])
substring_size = word_length * k
word_count = collections.Counter(words)
def sliding_window(left):
words_found = collections.defaultdict(int)
words_used = 0
excess_word = False
# Do the same iteration pattern as the previous approach - iterate
# word_length at a time, and at each iteration we focus on one word
for right in range(left, n, word_length):
if right + word_length > n:
break
sub = s[right : right + word_length]
if sub not in word_count:
# Mismatched word - reset the window
words_found = collections.defaultdict(int)
words_used = 0
excess_word = False
left = right + word_length # Retry at the next index
else:
# If we reached max window size or have an excess word
while right - left == substring_size or excess_word:
# Move the left bound over continously
leftmost_word = s[left : left + word_length]
left += word_length
words_found[leftmost_word] -= 1
if words_found[leftmost_word] == word_count[leftmost_word]:
# This word was the excess word
excess_word = False
else:
# Otherwise we actually needed it
words_used -= 1
# Keep track of how many times this word occurs in the window
words_found[sub] += 1
if words_found[sub] <= word_count[sub]:
words_used += 1
else:
# Found too many instances already
excess_word = True
if words_used == k and not excess_word:
# Found a valid substring
answer.append(left)
answer = []
for i in range(word_length):
sliding_window(i)
return answer
Complexity
- Given \(n\) as the length of \(s\), \(a\) as the length of words, and \(b\) as the length of each word:
- Time: \(O(a + n \cdot b)\)
- First, let’s analyze the time complexity of slidingWindow(). The for loop in this function iterates from the starting index left up to n, at increments of wordLength. This results in n / b total iterations. At each iteration, we create a substring of length wordLength, which costs \(O(b)\).
- Although there is a nested while loop, the left pointer can only move over each word once, so this inner loop will only ever perform a total of \(\frac{n}{wordLength}\) iterations summed across all iterations of the outer for loop. Inside that while loop, we also take a substring which costs \(O(b)\), which means each iteration will cost at most \(O(2 \cdot b)\) on average.
- This means that each call to
slidingWindowcosts \(O(\dfrac{n}{b} \cdot 2 \cdot b)\), or \(O(n)\). How many times do we call slidingWindow? wordLength, or \(b\) times. This means that all calls to slidingWindow costs \(O(n \cdot b)\). - On top of the calls to
slidingWindow, at the start of the algorithm we create a dictionary wordCount by iterating through words, which costs \(O(a)\). This gives us our final time complexity of \(O(a + n \cdot b)\). - Notice that the length of words \(a\) is not multiplied by anything, which makes this approach much more efficient than the first approach due to the bounds of the problem, as \(n > a \gg b\).
- Space: \(O(a + b)\)
- Most of the times, the majority of extra memory we use is due to the hash tables used to store word counts. In the worst-case scenario where words only has unique elements, we will store up to \(a\) keys in the tables.
- We also store substrings in sub which requires \(O(b)\) space. So the total space complexity of this approach is \(O(a + b)\). However, because for this particular problem the upper bound for \(b\) is very small (30), we can consider the space complexity to be \(O(a)\).
[76/Hard] Minimum Window Substring
Problem
-
Given two strings
sandtof lengthsmandnrespectively, return the minimum window substring ofssuch that every character int(including duplicates) is included in the window. If there is no such substring, return the empty string"". -
A substring is a contiguous sequence of characters within the string.
-
Example 1:
Input: s = "ADOBECODEBANC", t = "ABC"
Output: "BANC"
Explanation: The minimum window substring "BANC" includes 'A', 'B', and 'C' from string t.
- Example 2:
Input: s = "a", t = "a"
Output: "a"
Explanation: The entire string s is the minimum window.
- Example 3:
Input: s = "a", t = "aa"
Output: ""
Explanation: Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
- Constraints:
m == s.lengthn == t.length1 <= m, n <= 105s and t consist of uppercase and lowercase English letters.
- See problem on LeetCode.
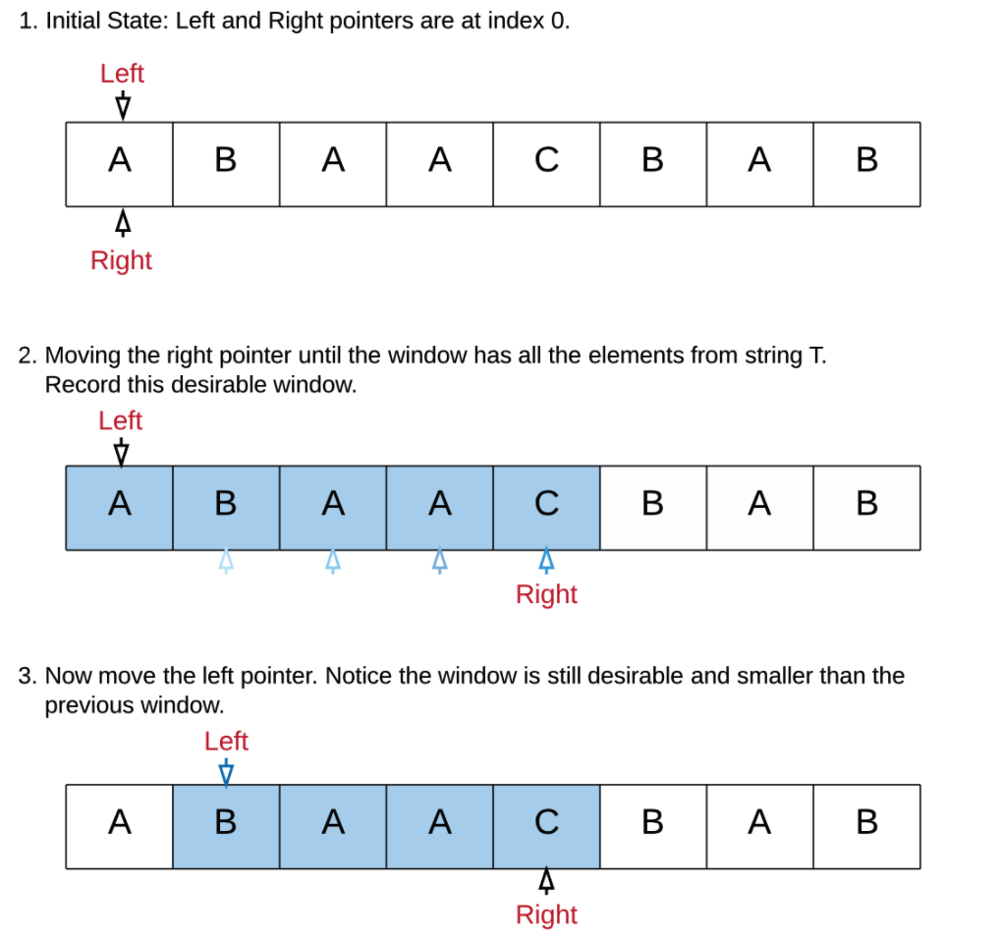
Solution: Maintain number of times a char is needed and overall missing chars; run a sliding window
- Idea:
- The current window is
s[i:j]and the result window iss[windowStart:windowEnd]. Inneed[char], store how many times charactercharis needed (can be negative) andmissingtells how many characters are still missing. In the loop, first add the new character to the window. Then, if nothing is missing, remove as much as possible from the window start and then update the result.
- The current window is
- Algorithm:
- Create a dict for the target list
need = collections.Counter(t). - Meanwhile create a empty dict for slidewindow.
- Set two point left and right from the beginning
- Valid is to calculate the item in slidewindow,the valid variable represents the number of characters in the window that meet the need condition. If the size of valid and dict_t.size() is the same, it means that the window has met the condition - and has completely covered the string T.
- Pattern for sliderwindow:
- Create a dict for the target list
class Solution:
def minWindow(self, s: str, t: str) -> str:
# hash table to store the required char frequency
need = collections.Counter(t)
# total character count we need to care about
missing = len(t)
# windowStart and windowEnd to be
windowStart, windowEnd = 0, 0
i = 0
# iterate over s starting over index 1
for j, char in enumerate(s, 1):
# if char is needed, then decrease missing (since we now have it)
if need[char] > 0:
missing -= 1
# decrease the freq of char from need (can be negative - which basically denotes
# that we have few extra characters which are not required but present in between current window)
need[char] -= 1
# we found a valid window
if missing == 0:
# trim chars from start to find the real windowStart
while i < j and need[s[i]] < 0:
# we're moving ahead (with i += 1 down below) so add to need[s[i]]
need[s[i]] += 1
# march ahead
i += 1
# if it's only one char case or curr window is smaller, then update window
if windowEnd == 0 or j-i < windowEnd-windowStart:
windowStart, windowEnd = i, j
# now reset the window to explore smaller windows
# make sure the first appearing char satisfies need[char]>0 (since we're )
need[s[i]] += 1
# missed this first char, so add missing by 1
missing += 1
#update i to windowStart+1 for next window
i += 1
return s[windowStart:windowEnd]
Complexity
- Time: \(O(n^2)\)
- Space: \(O(n)\) for
need
[167/Medium] Two Sum II - Input Array Is Sorted
Problem
-
Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order, find two numbers such that they add up to a specific target number. Let these two numbers be
numbers[index1]andnumbers[index2]where1 <= index1 < index2 <= numbers.length. -
Return the indices of the two numbers,
index1andindex2, added by one as an integer array[index1, index2]of length 2. -
The tests are generated such that there is exactly one solution. You may not use the same element twice.
-
Your solution must use only constant extra space.
-
Example 1:
Input: numbers = [2,7,11,15], target = 9
Output: [1,2]
Explanation: The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return [1, 2].
- Example 2:
Input: numbers = [2,3,4], target = 6
Output: [1,3]
Explanation: The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return [1, 3].
- Example 3:
Input: numbers = [-1,0], target = -1
Output: [1,2]
Explanation: The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return [1, 2].
- Constraints:
2 <= numbers.length <= 3 * 104-1000 <= numbers[i] <= 1000numbers is sorted in non-decreasing order.-1000 <= target <= 1000The tests are generated such that there is exactly one solution.
- See problem on LeetCode.
Solution: Sliding Window
- Follow the solution to Two Sum. The only change made below was to change the order of line #4. In the previous example, the order didn’t matter. But, here the problem asks for ascending order and since the values/indices in seen has always lower indices than your current number, it should come first. Also, note that the problem says it’s not zero based, meaning that indices don’t start from zero, which is why 1 was added to both of them.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
seen = {}
for i, value in enumerate(numbers):
remaining = target - numbers[i]
if remaining in seen:
return [seen[remaining]+1, i+1] #4
else:
seen[value] = i
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Two Pointers
- A better approach to solve this problem is to treat it as a two pointer problem. Since the array is already sorted, this works.
- You see the following approach in a lot of problems. What you want to do is to have two pointer (if it was 3sum, you’d need three pointers). One pointer move from left and one from right.
- Let’s say you have
numbers = [1,3,6,9]and yourtarget = 10. Now, left points to 1 at first, and right points to 9. There are three possibilities. If you sum numbers that left and right are pointing at, you gettemp_sum(line #1). If temp_sum is your target, you’re done! You’ll return it (line #9). - If it’s more than your target, it means that right is pointing to a very large value (line #5) and you need to bring it a little bit to the left to a smaller (or maybe an equal) value (line #6) by adding one to the index. If the
temp_sumis less than target (line #7), then you need to move your left to a little bit larger value by adding one to the index (line #9). This way, you try to narrow down the range in which you’re looking at and will eventually find a couple of number that sum to target, then, you’ll return this in line #9. - In this problem, since it says there is only one solution, nothing extra is necessary. However, when a problem asks to return all combinations that sum to target, you can’t simply return the first instance and you need to collect all the possibilities and return the list altogether (you’ll see something like this in 3sum).
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for left in range(len(numbers) -1): #1
right = len(numbers) - 1 #2
while left < right: #3
temp_sum = numbers[left] + numbers[right] #4
if temp_sum > target: #5
right -= 1 #6
elif temp_sum < target: #7
left +=1 #8
else:
return [left+1, right+1] #9
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[198/Medium] House Robber
Problem
-
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
-
Given an integer array
numsrepresenting the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police. -
Example 1:
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
- Example 2:
Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
- Constraints:
1 <= nums.length <= 1000 <= nums[i] <= 400
- See problem on LeetCode.
Solution: Recursion
- Recurrence relation:
rob(i) = max(rob(i - 2) + currentHouseValue, rob(i - 1))
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) <= 2:
return max(nums)
return self.robMax(nums, len(nums) - 1) # start from the last/top
def robMax(self, nums, i):
if i < 0:
return 0 # when i < 0 we just have to return 0
return max(nums[i] + self.robMax(nums, i - 2), self.robMax(nums, i - 1))
Complexity
- Time: \(O(2^n)\)
- Space: \(O(n)\)
Solution: Recursive/Top-Down DP
class Solution:
def rob(self, nums: List[int]) -> int:
def robMax(nums, dp, i):
if i < 0:
return 0
# Look Before You Leap (LBYL)
if dp[i] != -1: # if the value of dp[i] is not default i.e. -1 that means we have already calculated it so we dont have to do it again we just have to return it
return dp[i]
dp[i] = max(nums[i] + robMax(nums, dp, i - 2), robMax(nums, dp, i - 1))
return dp[i]
if len(nums) <= 2:
return max(nums)
dp = [-1 for _ in range(len(nums))] # cache
return robMax(nums, dp, len(nums) - 1)
Solution: Iterative/Bottom-Up DP
- Algorithm:
- For each house, the robber has two choices - to rob or not to rob. Also, you can only rob when you didn’t rob the previous house. Here, we create a DP table with size
len(nums)anddp[i]represents the maximum amount of money you can rob until the \(i^{th}\) house. The goal of this problem is to calculatedp[-1], which is the maximum amount of money you can rob until the last day. - Now, let’s write a formula for the two options we have at every stage:
- If you robbed the \((i - 2)^th\) house (and thus didn’t rob the previous \((i - 1)^th\) house, since you cannot rob adjacent houses), you can rob the current \(i^{th}\) house. This can be written as
dp[i - 2] + nums[i], becausedp[i - 2]denotes the maximum amount of money you can rob for the \((i - 2)^th\) house, and since you haven’t robbed the \(i_th\) house, you can add \(nums[i]\). - If you robbed on the previous \((i - 1)^th\) house, you can’t rob the current house. This can be written as \(dp[i - 1]\).
- If you robbed the \((i - 2)^th\) house (and thus didn’t rob the previous \((i - 1)^th\) house, since you cannot rob adjacent houses), you can rob the current \(i^{th}\) house. This can be written as
- You can choose the maximum value between these two choices above, and the larger one is the maximum amount you can rob up until the \(i^{th}\) house. This gives us the the following recurrence formula:
dp[i] = max(nums[i - 2] + nums[i], dp[i - 1])
- For each house, the robber has two choices - to rob or not to rob. Also, you can only rob when you didn’t rob the previous house. Here, we create a DP table with size
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums) < 3:
return max(nums)
dp = [0] * len(nums)
# the base cases where dp[0] is the amount you can take from 1 house and
# dp[1] is the amount you can take from 2 houses (that will be the maximum of nums[0] and nums[1])
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for num in range(2, len(nums)):
# take max of (i) the current house and two houses (i - 2) before the current house, and
# (ii) take all the gains we made up to the previous house.
# (since we cannot rob adjacent houses)
dp[num] = max(nums[num] + dp[num-2], dp[num-1]) # the recurrence relation
return dp[-1] # the last value will be your maximum amount of robbery
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: Sliding window; just book-keep the last two values
-
In the above solution, if we notice carefully we just need the last two values and not a whole array so we can further optimize it.
-
Note that in calculating
dp[i], you are just referencingdp[i - 2]anddp[i - 1]. In other words, all you need is the two values (max until the previous house and the house before), and you can discard the old values in the DP table.
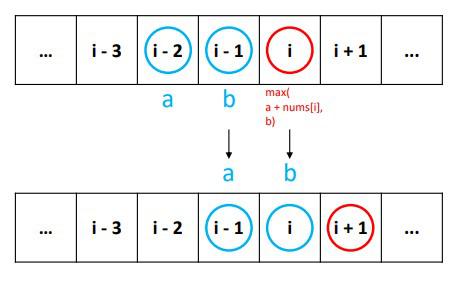
- Let
a(rob1orprevin the below solutions) be the maximum robbed amount corresponding to the \((i - 2)^th\) house, and letb(rob2orcurrin the below solutions) be the maximum robbed amount corresponding to the \((i - 1)^th\) house, today’s maximum would bemax(a + nums[i], b). And for the next house \(i\), this the maximum for the house before (i.e., the \((i - 1)^th\) house), and the maximum of the \((i - 2)^th\) house is nowb. So you can write this formula:
a, b = b, max(a + nums[i], b)
- This indicates new
ais replaced withb, and newbis replaced withmax(a + nums[i], b). By repeating this, you can calculate until the last day without storing all the values along the way. Finally,bat the end is what you want. So you can write the improved version.
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) <= 2:
return max(nums)
rob1, rob2 = nums[0], max(nums[0], nums[1])
for n in nums[2:]:
temp = max(rob1 + n, rob2) # the max amount we can rob from the given house and from the prev's previous and from the previous house
rob1, rob2 = rob2, temp # update both the variables
return temp # return the max amount
- Get rid of the
tempvariable:
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) <= 2:
return max(nums)
rob1, rob2 = nums[0], max(nums[0], nums[1])
for n in nums[2:]:
# the max amount we can rob from the given house and from the prev's previous and from the previous house
rob1, rob2 = rob2, max(rob1 + n, rob2) # update both the variables
return rob2 # return the max amount
- Simplified:
class Solution:
def rob(self, nums: List[int]) -> int:
prev, curr = 0
# every loop, calculate the maximum cumulative amount of money until current house
for i in nums:
# as the loop begins,curr represents dp[k-1],prev represents dp[k-2]
# dp[k] = max{ dp[k-1], dp[k-2] + i }
prev, curr = curr, max(curr, prev + i)
# as the loop ends,curr represents dp[k],prev represents dp[k-1]
return curr
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[904/Medium] Fruit Into Baskets
Problem
-
You are visiting a farm that has a single row of fruit trees arranged from left to right. The trees are represented by an integer array fruits where
fruits[i]is the type of fruit theithtree produces. -
You want to collect as much fruit as possible. However, the owner has some strict rules that you must follow:
-
You only have two baskets, and each basket can only hold a single type of fruit. There is no limit on the amount of fruit each basket can hold. Starting from any tree of your choice, you must pick exactly one fruit from every tree (including the start tree) while moving to the right. The picked fruits must fit in one of your baskets. Once you reach a tree with fruit that cannot fit in your baskets, you must stop. Given the integer array
fruits, return the maximum number of fruits you can pick. -
Example 1:
Input: fruits = [1,2,1]
Output: 3
Explanation: We can pick from all 3 trees.
- Example 2:
Input: fruits = [0,1,2,2]
Output: 3
Explanation: We can pick from trees [1,2,2].
If we had started at the first tree, we would only pick from trees [0,1].
- Example 3:
Input: fruits = [1,2,3,2,2]
Output: 4
Explanation: We can pick from trees [2,3,2,2].
If we had started at the first tree, we would only pick from trees [1,2].
- Constraints:
1 <= fruits.length <= 1050 <= fruits[i] < fruits.length
- See problem on LeetCode.
Solution: Sliding Window
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
fruit_types = Counter()
distinct = 0
max_fruits = 0
left = right = 0
while right < len(fruits):
# check if it is a new fruit, and update the counter
if fruit_types[fruits[right]] == 0:
distinct += 1
fruit_types[fruits[right]] += 1
# too many different fruits, so start shrinking window
while distinct > 2:
fruit_types[fruits[left]] -= 1
if fruit_types[fruits[left]] == 0:
distinct -= 1
left += 1
# set max_fruits to the max window size
max_fruits = max(max_fruits, right-left+1)
right += 1
return max_fruits
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[1291/Medium] Sequential Digits
Problem
-
An integer has sequential digits if and only if each digit in the number is one more than the previous digit.
-
Return a sorted list of all the integers in the range
[low, high]inclusive that have sequential digits. -
Example 1:
Input: low = 100, high = 300
Output: [123,234]
- Example 2:
Input: low = 1000, high = 13000
Output: [1234,2345,3456,4567,5678,6789,12345]
- Constraints:
10 <= low <= high <= 10^9
- See problem on LeetCode.
Solution: Start with a defined set of digits and run a sliding window
- One might notice that all integers that have sequential digits are substrings of string “123456789”. Hence to generate all such integers of a given length, just move the window of that length along “123456789” string.
- The advantage of this method is that it will generate the integers that are already in the sorted order.
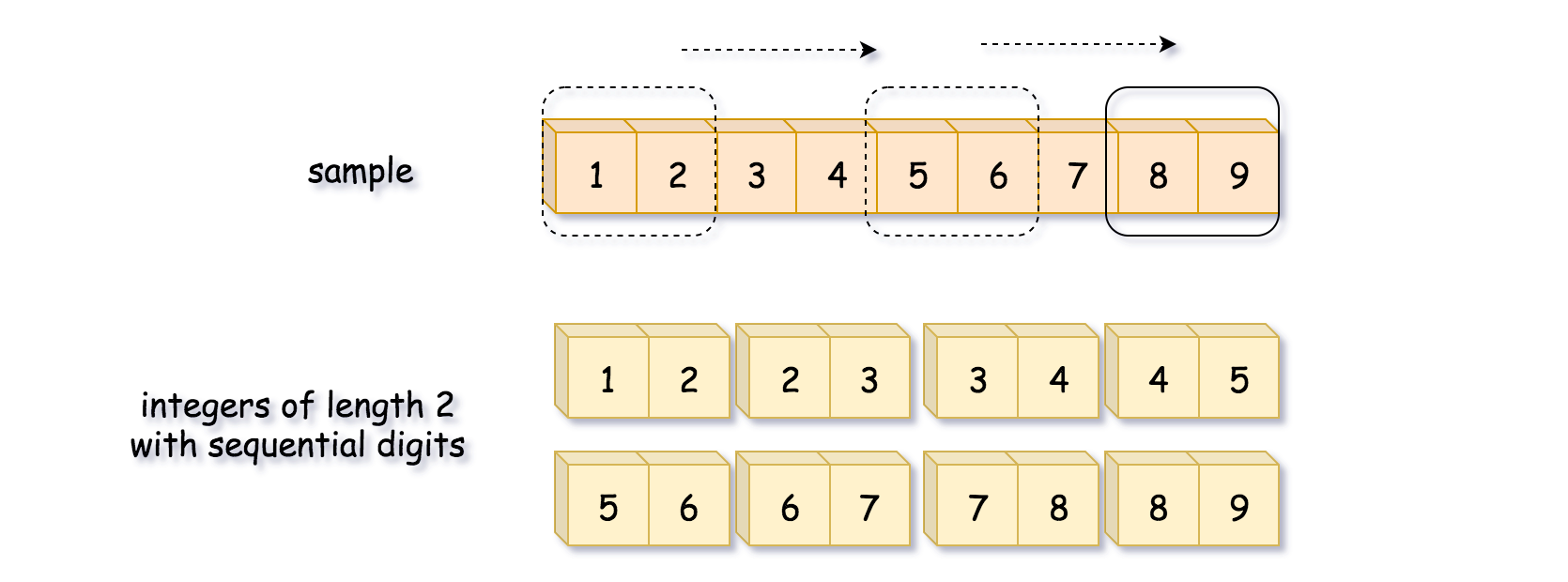
- Algorithm:
- Initialize sample string “123456789”. This string contains all integers that have sequential digits as substrings. Let’s implement sliding window algorithm to generate them.
- Iterate over all possible string lengths: from the length of
lowto the length ofhigh.- For each length iterate over all possible start indexes: from
0to10 - length.- Construct the number from digits inside the sliding window of current length.
- Add this number in the output list
nums, if it’s greater thanlowand less thanhigh.
- For each length iterate over all possible start indexes: from
- Return
nums.
class Solution:
def sequentialDigits(self, low: int, high: int) -> List[int]:
digits = "123456789"
nums = []
# Iterate over all possible string lengths: from the length of low to the length of high.
for length in range(len(str(low)), len(str(high)) + 1):
# For each length iterate over all possible start indexes: from 0 to len(digits) - length.
for start in range(len(digits) - length):
num = int(digits[start: start + length])
# Construct the number from digits inside the sliding window of current length.
if low <= num <= high:
# or if num >= low and num <= high:
# Add this number in the output list nums, if it's greater than low and less than high.
nums.append(num)
return nums
Complexity
- Time: \(O(9*9)=O(36)=O(1)\). Length of the
digitsstring is 9, and lengths oflowandhighare between 2 and 9. Hence the nested loops are executed no more than \(8 \times 8 = 64\) times.- Actually, there are 36 integers with the sequential digits. Here is how we calculate it. Starting from 9 digits in the sample string, one could construct 9 - 2 + 1 = 8 integers of length 2, 9 - 3 + 1 = 7 integers of length 3, and so on and so forth. In total, it would make 8 + 7 + … + 1 = 36 integers.
-
Space: \(O(9*9)=O(36)=O(1)\). To keep not more than 36 integers with sequential digits.
- Similar approach, worse runtime:
class Solution:
def sequentialDigits(self, low: int, high: int) -> List[int]:
digits = "123456789"
nums = []
for i in range(len(digits)):
for j in range(i+1, len(digits)):
num = int(digits[i:j+1])
if low <= num <= high:
# or if num >= low and num <= high:
nums.append(num)
return nums
Complexity
- Time: \(O(8*8)=O(36)=O(1)\). Length of the
digitsstring is 9, and lengths oflowandhighare between 2 and 9. Hence the nested loops are executed no more than \(8 \times 8 = 64\) times.- Actually, there are 36 integers with the sequential digits. Here is how we calculate it. Starting from 9 digits in the sample string, one could construct 9 - 2 + 1 = 8 integers of length 2, 9 - 3 + 1 = 7 integers of length 3, and so on and so forth. In total, it would make 8 + 7 + … + 1 = 36 integers.
- Space: \(O(8*8)=O(36)=O(1)\). To keep not more than 36 integers with sequential digits.