Distilled • LeetCode • Misc
- Pattern: Misc
- [Easy] Simple Moving Average
- [2/Medium] Add Two Numbers
- [7/Medium] Reverse Integer
- [8/Medium] String to Integer (atoi)
- [9/Easy] Palindrome Number
- [14/Easy] Longest Common Prefix
- [21/Easy] Merge Two Sorted Lists
- [31/Medium] Next Permutation
- [43/Medium] Multiply Strings
- [68/Hard] Valid Sudoku
- [68/Hard] Text Justification
- [50/Medium] Pow(x, n)
- [53/Easy] Maximum Subarray
- [54/Medium] Spiral Matrix
- [56/Medium] Merge intervals
- [57/Medium] Insert Interval
- [62/Medium] Unique Paths
- [65/Hard] Valid number
- [67/Easy] Add Binary
- [87/Hard] Scramble String
- [88/Easy] Merge Sorted Arrays
- [100/Easy] Same Tree
- [114/Medium] Flatten Binary Tree to Linked List
- [134/Medium] Gas Station
- [138/Medium] Copy List with Random Pointer
- [143/Medium] Reorder List
- [148/Medium] Sort List
- [158/Hard] Read N Characters Given read4 II - Call Multiple Times
- [203/Easy] Remove Linked List Elements
- [206/Easy] Reverse Linked List
- [214/Hard] Shortest Palindrome
- [228/Easy] Summary Ranges
- [238/Medium] Product of Array Except Self
- [252/Easy] Meeting Rooms
- [253/Easy] Meeting Rooms II
- [270/Easy] Closest Binary Search Tree Value
- [277/Medium] Find the Celebrity
- [283/Easy] Move Zeroes
- [289/Medium] Game of Life
- [Easy] Moving Average with Cold Start
- [346/Easy] Moving Average from Data Stream
- [383/Easy] Ransom Note
- [384/Medium] Shuffle an Array
- [398/Medium] Random Pick Index
- [409/Easy] Longest Palindrome
- [415/Easy] Add Strings
- [435/Medium] Non-overlapping Intervals
- [442/Medium] Find All Duplicates in an Array
- [443/Medium] String Compression
- [523/Medium] Continuous Subarray Sum
- [556/Medium] Next Greater Element III
- [567/Medium] Permutation in String
- [665/Medium] Non-decreasing Array
- [670/Medium] Maximum Swap
- [674/Easy] Longest Continuous Increasing Subsequence/Subarray
- [681/Medium] Next Closest Time
- [682/Easy] Baseball Game
- [683/Hard] K Empty Slots
- [686/Medium] Repeated String Match
- [708/Medium] Insert into a Sorted Circular Linked List
- [766/Easy] Toeplitz Matrix
- [771/Easy] Jewels and Stones
- [778/Hard] Swim in Rising Water
- [791/Medium] Custom Sort String
- [792/Medium] Number of Matching Subsequences
- [796/Easy] Rotate String
- [953/Easy] Verifying an Alien Dictionary/Mapping to Normal Order
- [989/Easy] Add to Array-Form of Integer
- [1108/Easy] Defanging an IP Address
- [1111/Medium] Maximum Nesting Depth of Two Valid Parentheses Strings
- [1268/Medium]
- [1288/Medium] Remove Covered Intervals
- [1344/Medium] Angle Between Hands of a Clock
- [1389/Easy] Create Target Array in the Given Order
- [1446/Easy] Consecutive Characters
- [1480/Easy] Running Sum of 1D Array
- [1570/Medium] Dot Product of Two Sparse Vectors
- [1662/Easy] Check If Two String Arrays are Equivalent
- [1629/Easy] Slowest Key
- [1641/Medium] Count Sorted Vowel Strings
- [1678/Easy] Goal Parser Interpretation
- [1732/Easy] Find the Highest Altitude
- [1762/Medium] Buildings With an Ocean View
- [1650/Medium] Lowest Common Ancestor of a Binary Tree III
- [1887/Medium] Reduction Operations to Make the Array Elements Equal
- [1911/Medium] Maximum Alternating Subsequence Sum
- [1920/Easy] Build Array from Permutation
- [2042/Easy] Check if Numbers Are Ascending in a Sentence
- [2060/Hard] Check if an Original String Exists Given Two Encoded Strings
- [2108/Easy] Find First Palindromic String in the Array
Pattern: Misc
[Easy] Simple Moving Average
Problem
- Given a list, calculate a moving average of a window of size
windowSizeof numbers. - Example:
Input:
a = [3, 1, 10, 3, 5]
windowSize = 2
Output:
2.0
5.5
6.5
4.0
Solution
if windowSize > len(a):
return -1
# Get the first window.
currSum = sum(a[0:windowSize])
print(currSum/windowSize)
# Slide the window from left to right.
for i in range(len(a) - windowSize):
currSum += a[windowSize+i]
currSum -= a[i]
print(currSum/windowSize)
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[2/Medium] Add Two Numbers
Problem
-
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
-
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
-
Example 1:
Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [7,0,8]
Explanation: 342 + 465 = 807.
- Example 2:
Input: l1 = [0], l2 = [0]
Output: [0]
- Example 3:
Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
Output: [8,9,9,9,0,0,0,1]
- Constraints:
The number of nodes in each linked list is in the range [1, 100].0 <= Node.val <= 9It is guaranteed that the list represents a number that does not have leading zeros.
- See problem on LeetCode.
Solution: Maintain carry and use divmod
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
carry = 0
res = n = ListNode(0)
while l1 or l2 or carry:
if l1:
carry += l1.val
l1 = l1.next
if l2:
carry += l2.val
l2 = l2.next
carry, val = int(carry) // 10, int(carry) % 10 # or divmod(carry, 10)
n.next = n = ListNode(val) # or the traditional "n.next = ListNode(val); n = n.next"
return res.next;
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[7/Medium] Reverse Integer
Problem
-
Given a signed 32-bit integer
x, returnxwith its digits reversed. If reversingxcauses the value to go outside the signed 32-bit integer range[-2^31, 2^31 - 1], then return0. -
Assume the environment does not allow you to store 64-bit integers (signed or unsigned).
-
Example 1:
Input: x = 123
Output: 321
- Example 2:
Input: x = -123
Output: -321
- Example 3:
Input: x = 120
Output: 21
- Constraints:
-2^31 <= x <= 2^31 - 1
- See problem on LeetCode.
Solution: Convert to str, reverse str and add sign
class Solution(object):
def reverse(self, x: int) -> int:
# extract the sign
s = (x > 0) - (x < 0)
# or cmp(x, 0) which returns negative if x<y, zero if x==y, positive if x>y.
# Change the sign to + for negative numbers since
# [::-1] would move the - sign to the end.
# Note that for positive numbers, this is a no op.
r = int(str(x * s)[::-1])
# Put the sign back.
return s * r * (r < 2**31)
Complexity
- Time: \(O(n + n) = O(n)\)
- Space: \(O(1)\)
[8/Medium] String to Integer (atoi)
Problem
-
Implement the
myAtoi(string s)function, which converts a string to a 32-bit signed integer (similar to C/C++’satoifunction). -
The algorithm for
myAtoi(string s)is as follows:- Read in and ignore any leading whitespace.
- Check if the next character (if not already at the end of the string) is ‘-‘ or ‘+’. Read this character in if it is either. This determines if the final result is negative or positive respectively. Assume the result is positive if neither is present.
- Read in next the characters until the next non-digit character or the end of the input is reached. The rest of the string is ignored.
- Convert these digits into an integer (i.e., “123” -> 123, “0032” -> 32). If no digits were read, then the integer is 0. Change the sign as necessary (from step 2).
- If the integer is out of the 32-bit signed integer range
[-2^31, 2^31 - 1], then clamp the integer so that it remains in the range. Specifically, integers less than -2^31 should be clamped to -2^31, and integers greater than 1. 2^31 - 1 should be clamped to 2^31 - 1. - Return the integer as the final result.
- Note:
- Only the space character ‘ ‘ is considered a whitespace character.
- Do not ignore any characters other than the leading whitespace or the rest of the string after the digits.
- Example 1:
Input: s = "42"
Output: 42
Explanation: The underlined characters are what is read in, the caret is the current reader position.
Step 1: "42" (no characters read because there is no leading whitespace)
^
Step 2: "42" (no characters read because there is neither a '-' nor '+')
^
Step 3: "42" ("42" is read in)
^
The parsed integer is 42.
Since 42 is in the range [-2^31, 2^31 - 1], the final result is 42.
- Example 2:
Input: s = " -42"
Output: -42
Explanation:
Step 1: " -42" (leading whitespace is read and ignored)
^
Step 2: " -42" ('-' is read, so the result should be negative)
^
Step 3: " -42" ("42" is read in)
^
The parsed integer is -42.
Since -42 is in the range [-2^31, 2^31 - 1], the final result is -42.
- Example 3:
Input: s = "4193 with words"
Output: 4193
Explanation:
Step 1: "4193 with words" (no characters read because there is no leading whitespace)
^
Step 2: "4193 with words" (no characters read because there is neither a '-' nor '+')
^
Step 3: "4193 with words" ("4193" is read in; reading stops because the next character is a non-digit)
^
The parsed integer is 4193.
Since 4193 is in the range [-2^31, 2^31 - 1], the final result is 4193.
- Constraints:
0 <= s.length <= 200s consists of English letters (lower-case and upper-case), digits (0-9), ' ', '+', '-', and '.'.
- See problem on LeetCode.
Solution: RegEx
class Solution(object):
def myAtoi(self, s: str) -> int:
"""
:type str: str
:rtype: int
"""
###better to do strip before sanity check (although 8ms slower):
#ls = list(s.strip())
#if len(ls) == 0 : return 0
if len(s) == 0:
return 0
ls = list(s.strip())
sign = -1 if ls[0] == '-' else 1
if ls[0] in ['-','+']:
del ls[0]
ret, i = 0, 0
while i < len(ls) and ls[i].isdigit():
ret = ret*10 + ord(ls[i]) - ord('0')
i += 1
return max(-2**31, min(sign * ret,2**31-1))
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
class Solution:
def myAtoi(self, s: str) -> int:
if len(s) == 0:
return 0
i = 0
while i < len(s) and s[i] == ' ':
i += 1
if i == len(s): # all are leading whitespace
return 0
if s[i]=='+':
sign = 1
i += 1
elif s[i]=='-':
sign = -1
i += 1
else:
sign = 1
val = 0
while i < len(s) and s[i].isdigit():
val = val*10 + ord(s[i]) - ord('0')
i += 1
res = val*sign
if res < -2**31: return -2**31
elif res > 2**31-1: return 2**31-1
else: return res
Complexity
- Time: \(O(n)\) where \(n = len(s)\)
- Space: \(O(1)\)
Solution: RegEx
class Solution:
# @return an integer
def myAtoi(self, s: str) -> int:
str = str.strip()
str = re.findall('(^[\+\-0]*\d+)\D*', str)
try:
result = int(''.join(str))
MAX_INT = 2147483647
MIN_INT = -2147483648
if result > MAX_INT > 0:
return MAX_INT
elif result < MIN_INT < 0:
return MIN_INT
else:
return result
except:
return 0
Complexity
- Time: \(O(n + n) = O(n)\)
- Space: \(O(1)\)
[9/Easy] Palindrome Number
Problem
-
Given an integer
x, return true if x is palindrome integer. -
An integer is a palindrome when it reads the same backward as forward.
-
For example,
121is a palindrome while123is not. -
Example 1:
Input: x = 121
Output: true
Explanation: 121 reads as 121 from left to right and from right to left.
- Example 2:
Input: x = -121
Output: false
Explanation: From left to right, it reads -121. From right to left, it becomes 121-. Therefore it is not a palindrome.
- Example 3:
Input: x = 10
Output: false
Explanation: Reads 01 from right to left. Therefore it is not a palindrome.
- Constraints:
-2^31 <= x <= 2^31 - 1
-
Follow up: Could you solve it without converting the integer to a string?
- See problem on LeetCode.
Solution: Convert the number to string and compare it with the reversed string
-
This is the easiest way to check if integer is palindrome.
-
Convert the number to string and compare it with the reversed string.
class Solution:
def isPalindrome(self, x: int) -> bool:
if x < 0:
return False
return str(x) == str(x)[::-1]
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for storing the reversed integer
Solution: Don’t convert the number to string, recreate a new number in reverse order
class Solution:
def isPalindrome(self, x: int) -> bool:
if x < 0:
return False
inputNum = x
newNum = 0
# reverse number
while x:
newNum = newNum * 10 + x % 10
x = x // 10
return newNum == inputNum
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for storing the reversed integer
Solution: Instead of reversing the whole integer, let’s convert half of the integer and then check if it’s palindrome
-
Instead of reversing the whole integer, let’s convert half of the integer and then check if it’s palindrome. How do we know when we’ve reached the half? Check if our new half is greater than the original one.
-
For e.g.,
Even case:
If x = 1234, then let's reverse x with a loop.
Initially, x = 1234, result = 0
Loop iteration #1: x = 123, result = 1
Loop iteration #2: x = 12, result = 12
Odd case:
If x = 15951, then let's reverse x with a loop.
Initially, x = 15951, result = 0
Loop iteration #1: x = 1595, result = 1
Loop iteration #2: x = 159, result = 15
Loop iteration #3: x = 15, result = 159
-
We see that
result > xafter3loops and we’ve crossed the digits of the integer half way the integer because it’s an integer of odd length. If it’s an even length integer, the loop stops exactly in the middle after iteration 2. -
Now we can compare
xandresultif the integer has an even length, orxandresult//10if the integer has an odd length and returnTrueif they match.
class Solution:
def isPalindrome(self, x: int) -> bool:
# if x is negative, return False. if x is positive and last digit is 0, that also cannot form a palindrome, return False.
if x < 0 or (x > 0 and x % 10 == 0):
return False
result = 0
# reverse number till the midpoint
while x > result:
result = result * 10 + x % 10
x = x // 10
return x == result or x == result // 10 # or return True if (x == result or x == result // 10) else False
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for storing the reversed integer
[14/Easy] Longest Common Prefix
Problem
-
Write a function to find the longest common prefix string amongst an array of strings.
-
If there is no common prefix, return an empty string
"". -
Example 1:
Input: strs = ["flower","flow","flight"]
Output: "fl"
- Example 2:
Input: strs = ["dog","racecar","car"]
Output: ""
Explanation: There is no common prefix among the input strings.
- Constraints:
1 <= strs.length <= 2000 <= strs[i].length <= 200strs[i] consists of only lower-case English letters.
- See problem on LeetCode.
Solution: Chop off the last character every iteration until the prefix fits the string
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
"""
:type strs: List[str]; rtype: str
"""
# early termination: if strs is None
if not strs:
return None
# early termination: if len(strs) is an iterable but has no strings inside
if not len(strs):
return None
prefix = strs[0] # or "min(strs, key=len)" or "sorted(strs, key=len)[0]"
for s in strs:
while s[:len(prefix)] != prefix: # or "while not s.startswith(prefix):"
# remove a character from "prefix" from the end
# until the prefix fits the string
prefix = prefix[:-1]
return prefix
Complexity
- Time: \(O(n^2)\)
- Space: \(O(1)\)
Solution: Aggregate the characters in each string by their positions and build the prefix incrementally until you hit >1 unique chars
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
"""
:type strs: List[str]; rtype: str
"""
# the zip() call here aggregates the characters in each string
# by their positions, so the prefix/initial characters
# feature first.
# for example:
# >>> strs = ["flower","flow","flight"]
# >>> aggregatedCharsByPos = zip(*strs) # <zip object at location>
# >>> list(aggregatedCharsByPos)
# [('f', 'f', 'f'), ('l', 'l', 'l'), ('o', 'o', 'i'), ('w', 'w', 'g')]
# note that if the length of the iterables are not equal,
# zip creates the list of tuples of length equal to the smallest iterable.
aggregatedCharsByPos, retVal = zip(*strs), ""
for ch in aggregatedCharsByPos:
# if there are >1 unique characters at the same position,
# get out of the loop since you have the longest prefix already
if len(set(ch)) > 1:
break
# build up return value
retVal += c[0]
return retVal
Complexity
- Time: \(O(n + n) = O(n)\)
- Space: \(O(1)\)
[21/Easy] Merge Two Sorted Lists
Problem
-
You are given the heads of two sorted linked lists
list1andlist2. -
Merge the two lists in a one sorted list. The list should be made by splicing together the nodes of the first two lists.
-
Return the head of the merged linked list.
-
Example 1:
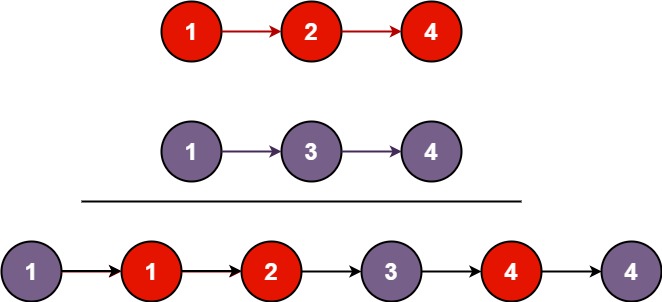
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]
- Example 2:
Input: list1 = [], list2 = []
Output: []
- Example 3:
Input: list1 = [], list2 = [0]
Output: [0]
- Constraints:
The number of nodes in both lists is in the range [0, 50].-100 <= Node.val <= 100Both list1 and list2 are sorted in non-decreasing order.
- See problem on LeetCode.
Solution
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
if list1 is None:
return list2
elif list2 is None:
return list1
elif list1.val <= list2.val:
list1.next = self.mergeTwoLists(list1.next, list2)
return list1
else:
list2.next = self.mergeTwoLists(list1, list2.next)
return list2
Complexity
- Time: \(O(m+n)\) where \(m\) and \(n\) are the lengths of the two lists respectively
- Space: \(O(1)\)
[31/Medium] Next Permutation
Problem
- A permutation of an array of integers is an arrangement of its members into a sequence or linear order.
- For example, for
arr = [1,2,3], the following are considered permutations of arr:[1,2,3], [1,3,2], [3,1,2], [2,3,1].
- For example, for
- The next permutation of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the next permutation of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
- For example, the next permutation of
arr = [1,2,3] is [1,3,2]. - Similarly, the next permutation of
arr = [2,3,1] is [3,1,2]. - While the next permutation of
arr = [3,2,1]is[1,2,3]because[3,2,1]does not have a lexicographical larger rearrangement.
- For example, the next permutation of
- Given an array of integers
nums, find the next permutation ofnums. -
The replacement must be in place and use only constant extra memory.
- Example 1:
Input: nums = [1,2,3]
Output: [1,3,2]
- Example 2:
Input: nums = [3,2,1]
Output: [1,2,3]
- Example 3:
Input: nums = [1,1,5]
Output: [1,5,1]
- Constraints:
1 <= nums.length <= 1000 <= nums[i] <= 100
- See problem on LeetCode.
Solution: Find the first non-increasing element
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
# To find next permutation, we'll start from the end.
i = j = len(nums)-1
# First we'll find the first non-increasing element starting from the end.
while i > 0 and nums[i-1] >= nums[i]:
i -= 1
# After completion of the first loop, there will be two cases:
# 1. "i" becomes zero (this will happen if the given array is sorted in decreasing order). In this case, simply reverse the sequence and return.
if i == 0:
nums.reverse()
return
# 2. If "i" is not zero then we'll find the first number greater than nums[i-1] starting from end.
while nums[j] <= nums[i-1]:
j -= 1
# Now our i and j pointers are pointing at two different positions:
# i -> first non-ascending number from end
# j -> first number greater than nums[i-1]
# We'll swap these two numbers
nums[i-1], nums[j] = nums[j], nums[i-1]
# We'll reverse the sequence starting from i to end
nums[i:]= nums[len(nums)-1:i-1:-1]
# We don't need to return anything as we've modified nums in-place
-
Take an example from Nayuki and try to hand-trace the above code manually. This will better help to understand the code.
-
Related links:
Complexity
- Time: \(O(3n) = O(n)\)
- Space: \(O(1)\)
[43/Medium] Multiply Strings
-
Given two non-negative integers
num1andnum2represented as strings, return the product ofnum1andnum2, also represented as a string. -
Note: You must not use any built-in BigInteger library or convert the inputs to integer directly.
-
Example 1:
Input: num1 = "2", num2 = "3"
Output: "6"
- Example 2:
Input: num1 = "123", num2 = "456"
Output: "56088"
- Constraints:
1 <= num1.length, num2.length <= 200num1 and num2 consist of digits only.Both num1 and num2 do not contain any leading zero, except the number 0 itself.
- See problem on LeetCode.
Solution: Decode numbers, multiply them and encode them together
class Solution:
def multiply(self, num1: str, num2: str) -> str:
if num1 == '0' or num2 == '0':
return '0'
def decode(num):
ans = 0
for i in num:
ans = ans*10 + (ord(i) - ord('0'))
return ans
def encode(s):
news = ''
while s:
a = s % 10
s = s // 10
news = chr(ord('0') + a) + news
return news
return encode(decode(num1) * decode(num2))
- Same approach; differently structured:
class Solution(object):
def multiply(self, num1: str, num2: str) -> str:
"""
:type num1: str
:type num2: str
:rtype: str
"""
res = 0 # output
carry1 = 1 # carry1 takes care of num1
for i in num1[::-1]: # this goes over num1 from right to left as we do normal multiplication, in the above example first 3 and then 2.
carry2 = 1 # takes care of num2
for j in num2[::-1]: # this goes over num2 from right to left as we do normal multiplication, in the above example first 6 and then 3.
res += int(i)*int(j)*carry1*carry2 # this is each component calculated separately and added to res
carry2 *= 10 # after first iteration (number 6 is covered), it goes to the next number from right, which is 3 here, actually 30, right? That's why it multiplies the carry2 by 10. Similar for carry1.
carry1 *= 10
return str(res)
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[68/Hard] Valid Sudoku
Problem
- Determine if a
9 x 9Sudoku board is valid. Only the filled cells need to be validated according to the following rules:- Each row must contain the digits 1-9 without repetition.
- Each column must contain the digits 1-9 without repetition.
- Each of the nine
3 x 3sub-boxes of the grid must contain the digits 1-9 without repetition. Note: - A Sudoku board (partially filled) could be valid but is not necessarily solvable.
- Only the filled cells need to be validated according to the mentioned rules.
- Example 1:

Input: board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: true
- Example 2:
Input: board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.
- Constraints:
board.length == 9board[i].length == 9board[i][j] is a digit 1-9 or '.'.
- See problem on LeetCode.
Solution: Readable
def isValidSudoku(self, board):
return (self.is_row_valid(board) and
self.is_col_valid(board) and
self.is_square_valid(board))
def is_row_valid(self, board):
for row in board:
if not self.is_unit_valid(row):
return False
return True
def is_col_valid(self, board):
for col in zip(*board):
if not self.is_unit_valid(col):
return False
return True
def is_square_valid(self, board):
for i in (0, 3, 6):
for j in (0, 3, 6):
square = [board[x][y] for x in range(i, i + 3) for y in range(j, j + 3)]
if not self.is_unit_valid(square):
return False
return True
def is_unit_valid(self, unit):
unit = [i for i in unit if i != '.']
return len(set(unit)) == len(unit)
Solution: One-liner using Counter
def isValidSudoku(self, board):
return 1 == max(collections.Counter(
x
for i, row in enumerate(board)
for j, c in enumerate(row)
if c != '.'
for x in ((c, i), (j, c), (i/3, j/3, c))
).values() + [1])
- The
+ [1]is only for the empty board, wheremaxwould get an empty list and complain. It’s not necessary to get it accepted here, as the empty board isn’t among the test cases, but it’s good to have.
Solution: One-liner using len(set).
def isValidSudoku(self, board):
seen = sum(([(c, i), (j, c), (i/3, j/3, c)]
for i, row in enumerate(board)
for j, c in enumerate(row)
if c != '.'), [])
return len(seen) == len(set(seen))
Solution: One-liner using any.
def isValidSudoku(self, board):
seen = set()
return not any(x in seen or seen.add(x)
for i, row in enumerate(board)
for j, c in enumerate(row)
if c != '.'
for x in ((c, i), (j, c), (i/3, j/3, c)))
Solution: One-liner with iterating a different way
def isValidSudoku(self, board):
seen = sum(([(c, i), (j, c), (i/3, j/3, c)]
for i in range(9) for j in range(9)
for c in [board[i][j]] if c != '.'), [])
return len(seen) == len(set(seen))
[68/Hard] Text Justification
Problem
-
Given an array of strings words and a width maxWidth, format the text such that each line has exactly maxWidth characters and is fully (left and right) justified.
-
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces ‘ ‘ when necessary so that each line has exactly maxWidth characters.
-
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
-
For the last line of text, it should be left-justified and no extra space is inserted between words.
- Note:
- A word is defined as a character sequence consisting of non-space characters only.
- Each word’s length is guaranteed to be greater than 0 and not exceed maxWidth.
- The input array words contains at least one word.
- Example 1:
Input: words = ["This", "is", "an", "example", "of", "text", "justification."], maxWidth = 16
Output:
[
"This is an",
"example of text",
"justification. "
]
- Example 2:
Input: words = ["What","must","be","acknowledgment","shall","be"], maxWidth = 16
Output:
[
"What must be",
"acknowledgment ",
"shall be "
]
Explanation: Note that the last line is "shall be " instead of "shall be", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified becase it contains only one word.
- Example 3:
Input: words = ["Science","is","what","we","understand","well","enough","to","explain","to","a","computer.","Art","is","everything","else","we","do"], maxWidth = 20
Output:
[
"Science is what we",
"understand well",
"enough to explain to",
"a computer. Art is",
"everything else we",
"do "
]
- Constraints:
1 <= words.length <= 3001 <= words[i].length <= 20words[i] consists of only English letters and symbols.1 <= maxWidth <= 100words[i].length <= maxWidth
- See problem on LeetCode.
Solution: Two loops
class Solution:
def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:
ans, cur = [], []
chars = 0
for word in words:
# if cur is empty or the total chars + total needed spaces + next word fit
if not cur or (len(word) + chars + len(cur)) <= maxWidth:
cur.append(word)
chars += len(word)
else:
# place spaces, append the line to the ans, and move on
line = self.placeSpacesBetween(cur, maxWidth - chars)
ans.append(line)
cur.clear()
cur.append(word)
chars = len(word)
# left justify any remaining text, which is easy
if cur:
extra_spaces = maxWidth - chars - len(cur) + 1
ans.append(' '.join(cur) + ' ' * extra_spaces)
return ans
def placeSpacesBetween(self, words, spaces):
if len(words) == 1: return words[0] + ' ' * spaces
space_groups = len(words)-1
spaces_between_words = spaces // space_groups
extra_spaces = spaces % space_groups
cur = []
for word in words:
cur.append(word)
# place the min of remaining spaces or spaces between words plus an extra if available
cur_extra = min(1, extra_spaces)
spaces_to_place = min(spaces_between_words + cur_extra, spaces)
cur.append(' ' * spaces_to_place)
if extra_spaces: extra_spaces -= 1
spaces -= spaces_to_place
return ''.join(cur)
Complexity
- Time: \(O(n^2)\)
- Space: \(O(n)\)
Solution: Two loops; cleaner version
class Solution:
def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:
i, N, result = 0, len(words), []
while i < N:
# decide how many words to be put in one line
oneLine, j, currWidth, positionNum, spaceNum = [words[i]], i + 1, len(words[i]), 0, maxWidth - len(words[i])
while j < N and currWidth + 1 + len(words[j]) <= maxWidth:
oneLine.append(words[j])
currWidth += 1 + len(words[j])
spaceNum -= len(words[j])
positionNum, j = positionNum + 1, j + 1
i = j
# decide the layout of one line
if i < N and positionNum:
spaces = [' ' * (spaceNum // positionNum + (k < spaceNum % positionNum)) for k in range(positionNum)] + ['']
else: # last line or the line only has one word
spaces = [' '] * positionNum + [' ' * (maxWidth - currWidth)]
result.append(''.join([s for pair in zip(oneLine, spaces) for s in pair]))
return result
Complexity
- Time: \(O(n^2)\)
- Space: \(O(n)\)
Solution: Loop over once and adjust spacing
- We’ll build the result array line-by-line while iterating over words in the input. Whenever the current line gets too big, we’ll appropriately format it and proceed with the next line until for loop is over. Last but not least, we’ll need to left-justify the last line.
class Solution:
# Why slots: https://docs.python.org/3/reference/datamodel.html#slots
# TLDR: 1. faster attribute access. 2. space savings in memory.
# For letcode problems this can save ~ 0.1MB of memory <insert is something meme>
__slots__ = ()
def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:
# Init return array in which, we'll store justified lines
lines = []
# current line width
width = 0
# current line words
line = []
for word in words:
# Gather as many words that will fit under maxWidth restrictions.
# Line length is a sum of:
# 1) Current word length
# 2) Sum of words already in the current line
# 3) Number of spaces (each word needs to be separated by at least one space)
if (len(word) + width + len(line)) <= maxWidth:
width += len(word)
line.append(word)
continue
# If the current line only contains one word, fill the remaining string with spaces.
if len(line) == 1:
# Use the format function to fill the remaining string with spaces easily and readable.
# You could also do something like:
# line = " ".join(line)
# line += " " * (maxWidth - len(line))
# lines.append(line)
lines.append(
"{0: <{width}}".format( " ".join(line), width=maxWidth)
)
else:
# Else calculate how many common spaces and extra spaces are there for the current line.
# Example:
# line = ['a', 'computer.', 'Art', 'is']
# width left in line equals to: maxWidth - width: 20 - 15 = 5
# len(line) - 1 because to the last word, we aren't adding any spaces
# Now divmod will give us how many spaces are for all words and how many extra to distribute.
# divmod(5, 3) = 1, 2
# This means there should be one common space for each word, and for the first two, add one extra space.
space, extra = divmod(
maxWidth - width,
len(line) - 1
)
i = 0
# Distribute extra spaces first
# There cannot be a case where extra spaces count is greater or equal to number words in the current line.
while extra > 0:
line[i] += " "
extra -= 1
i += 1
# Join line array into a string by common spaces, and append to justified lines.
lines.append(
(" " * space).join(line)
)
# Create new line array with the current word in iteration, and reset current line width as well.
line = [word]
width = len(word)
# Last but not least format last line to be left-justified with no extra space inserted between words.
# No matter the input, there always be the last line at the end of for loop, which makes things even easier considering the requirement.
lines.append(
"{0: <{width}}".format(" ".join(line), width=maxWidth)
)
return lines
Complexity
- Time: \(O(n)\) since there is just one for loop, which iterates over words provided as input.
- Space: \(O(n + l)\) where \(n\) is the length of words, and \(l\) max length of words in one line. Worst case scenario \(l = n\), which will add up to \(O(2n)\) but in asymptotic analysis we don’t care about constants so final complexity is still linear.
[50/Medium] Pow(x, n)
Problem
-
Implement
pow(x, n), which calculates x raised to the powern(i.e.,x^n). -
Example 1:
Input: x = 2.00000, n = 10
Output: 1024.00000
- Example 2:
Input: x = 2.10000, n = 3
Output: 9.26100
- Example 3:
Input: x = 2.00000, n = -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25
- Constraints:
-100.0 < x < 100.0-2^31 <= n <= 2^31-1
- See problem on LeetCode.
Solution: Use “**”
class Solution:
myPow = pow
- That’s even shorter than the other more obvious “cheat”:
class Solution:
def myPow(self, x: float, n: int) -> float:
return x ** n
Solution: Recursion
class Solution:
def myPow(self, x: float, n: int) -> float:
if not n:
return 1
if n < 0:
return 1 / self.myPow(x, -n)
if n % 2:
return x * self.myPow(x, n-1)
return self.myPow(x*x, n/2)
Solution: Iteration
class Solution:
def myPow(self, x: float, n: int) -> float:
if n < 0:
x = 1 / x
n = -n
pow = 1
while n:
if n & 1:
pow *= x
x *= x
n >>= 1
return pow
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[53/Easy] Maximum Subarray
Problem
-
Given an integer array
nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum. -
A subarray is a contiguous part of an array.
-
Example 1:
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
- Example 2:
Input: nums = [1]
Output: 1
- Example 3:
Input: nums = [5,4,-1,7,8]
Output: 23
- Constraints:
1 <= nums.length <= 105-104 <= nums[i] <= 104
- See problem on LeetCode.
Solution: Kadane’s algorithm
- Read more on Wikipedia: Maximum subarray problem.
class Solution:
def maxSubArray(self, A):
"""
@param A, a list of integers
@return an integer
"""
# not needed if the question says that the array should have at least one number.
if not A:
return 0
curSum = maxSum = A[0]
for num in A[1:]:
# Check if we should abandon the accumulated value so far
# and start a new run of numbers if the previous sum is negative
curSum = max(num, curSum + num) # or curSum = max(curSum, 0) + num
# Update answer if current sum is better than the previous one
maxSum = max(maxSum, curSum)
return maxSum
- Same approach; rephrased longer answer:
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
max_so_far = curr_so_far = -float('inf')
for i in range(len(nums)):
curr_so_far += nums[i] # Add current number
# Check if we should abandon the accumulated value so far
# and start a new run of numbers if the previous sum is negative
curr_so_far = max(curr_so_far, nums[i])
# Update answer
max_so_far = max(max_so_far, curr_so_far)
return max_so_far
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[54/Medium] Spiral Matrix
Problem
-
Given an
m x nmatrix, return all elements of thematrixin spiral order. -
Example 1:
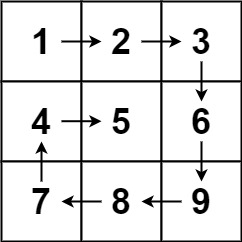
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]
- Example 2:
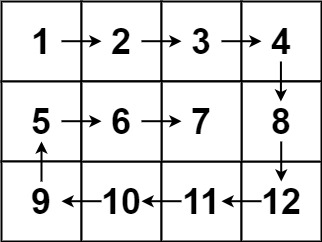
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]
- Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
- See problem on LeetCode.
Solution: Recursion
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
if len(matrix) == 0:
return []
new_matrix = []
for j in range(len(matrix[0])-1, -1, -1):
new_lst = []
for i in range(1, len(matrix)):
new_lst.append(matrix[i][j])
new_matrix.append(new_lst)
return matrix[0] + self.spiralOrder(new_matrix)
Solution: One-liner
- Take the first row plus the spiral order of the rotated remaining matrix.
def spiralOrder(self, matrix):
return matrix and [*matrix.pop(0)] + self.spiralOrder([*zip(*matrix)][::-1])
Solution
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
height = len(matrix)
width = len(matrix[0])
top = 0
bottom = height - 1
left = 0
right = width - 1
ans = []
while top < bottom and left < right:
for col in range(left, right):
ans.append(matrix[top][col])
for row in range(top, bottom):
ans.append(matrix[row][right])
for col in range(right, left, -1):
ans.append(matrix[bottom][col])
for row in range(bottom, top, -1):
ans.append(matrix[row][left])
top += 1
bottom -= 1
left += 1
right -= 1
# If a matrix remain inside it is either a 1xn or a mx1
# a linear scan will return the same order as spiral for these
if len(ans) < height*width:
for row in range(top, bottom+1):
for col in range(left, right+1):
ans.append(matrix[row][col])
return ans
- Here are 3 examples:
Example 1: row remains in middle
[1,2,3,4]
[5,6,7,8]
[9,0,1,2]
The bottom nested for loops will traverse (in-order): 6,7
Example 2: Single element remains in middle
[1,2,3]
[4,5,6]
[7,8,9]
The bottom nested for loops will traverse (in-order): 5
Example C: Column remains in middle
[1,2,3]
[4,5,6]
[7,8,9]
[0,1,2]
The bottom nested for loops will traverse (in-order): 5,8
- Same approach; no need to handle edge cases with this solution. We already know the length of our result list should be length of
m*n. So, just ignore the redundant elements and returnres[:m*n].
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m, n = len(matrix), len(matrix[0])
left, right, top, bottom = 0, n - 1, 0, m - 1
res = []
while left <= right and top <= bottom:
# top left to top right
for col in range(left, right+1):
res.append(matrix[top][col])
top += 1
# top right to right bottom
for row in range(top, bottom+1):
res.append(matrix[row][right])
right -= 1
# right bottom to right left
for col in range(right, left-1, -1):
res.append(matrix[bottom][col])
bottom -= 1
# left bottom to top left
for row in range(bottom, top-1, -1):
res.append(matrix[row][left])
left += 1
# just ignore the redundant and return length of m*n
return res[:m*n]
- Same approach (but with if-conditions so don’t have to restrict the length of
reswhen returning):
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m, n = len(matrix), len(matrix[0])
left, right, top, bottom = 0, n - 1, 0, m - 1
res = []
while left <= right and top <= bottom:
# top left to top right
for col in range(left, right+1):
res.append(matrix[top][col])
top += 1
# top right to right bottom
for row in range(top, bottom+1):
res.append(matrix[row][right])
right -= 1
if (top <= bottom):
# right bottom to right left
for col in range(right, left-1, -1):
res.append(matrix[bottom][col])
bottom -= 1
if (left <= right):
# left bottom to top left
for row in range(bottom, top-1, -1):
res.append(matrix[row][left])
left += 1
# just ignore the redundant and return length of m*n
return res
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m , n = len(matrix), len(matrix[0])
#refers to row as row can only move up or down
topBound , bottomBound = 0, m-1
#refers to cols as cols can only move right or left
leftBound, rightBound = 0, n-1
res = []
size = m*n
# we iterate until we have gone over all elements
while len(res) < size:
# we iterate until we have found the center
# or while leftBound <= rightBound and topBound <= bottomBound:
# runs through the first row straight through each col
if topBound <= bottomBound:
for col in range(leftBound, rightBound+1):
res.append(matrix[topBound][col])
topBound += 1
# next runs down the column
if leftBound <= rightBound:
for row in range(topBound, bottomBound+1):
res.append(matrix[row][rightBound])
rightBound -= 1
# goes right to left in col
if topBound <= bottomBound:
for col in range(rightBound, leftBound -1, -1):
res.append(matrix[bottomBound][col])
bottomBound -= 1
# goes up
if leftBound <= rightBound:
for row in range(bottomBound, topBound-1, -1):
res.append(matrix[row][leftBound])
leftBound += 1
return res
- Note that the
ifconditions are the “key” concept. This prevents the double counting, especially for cases where the middle most is “horizontal” or “vertical”:
1 2 3 4 or 1 2 3 or 1 2 3
5 * * 7 4 * 5 4 * 4
7 7 7 7 4 4 4 4 * 4
4 * 4
3 3 3
Complexity
- Time: \(O(H*W)\) since we traverse all elements in the matrix to be able to return them.
- Space: \(O(H*W)\) due to the size of the output variable (which is as large as the input matrix). If you don’t consider output variable size in your analysis then: \(O(1)\) space.
[56/Medium] Merge intervals
Problem
-
Given an array of
intervalswhereintervals[i] = [start_i, end_i], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input. -
Example 1:
Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].
- Example 2:
Input: intervals = [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considered overlapping.
- Constraints:
1 <= intervals.length <= 104intervals[i].length == 20 <= start_i <= end_i <= 104
- See problem on LeetCode.
Solution: sort first, then compare the start of the current interval with the end of the prior interval
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
out = []
for i in sorted(intervals, key=lambda i: i[0]):
# or for i in sorted(intervals, key=lambda i: i.start):
if out and i[0] <= out[-1][1]:
# or if out and i.start <= out[-1].end:
out[-1][1] = max(out[-1][1], i[1])
# or out[-1].end = max(out[-1].end, i.end)
else:
out += i, # Note that "i," is a tuple (because of the comma), and you can extend a tuple to a list (using "+=").
# or out += [i]
return out
- Similar: Meeting Rooms, Meeting Rooms II and Non-overlapping Intervals.
Complexity
- Time: \(O(n\log{n} + n) = O(n\log{n})\)
- Space: \(O(n)\)
[57/Medium] Insert Interval
Problem
- You are given an array of non-overlapping intervals
intervalswhereintervals[i] = [start_i, end_i]represent the start and the end of thei-thinterval and intervals is sorted in ascending order bystart_i. You are also given an intervalnewInterval = [start, end]that represents the start and end of another interval. - Insert
newIntervalintointervalssuch thatintervalsis still sorted in ascending order bystart_iand intervals still does not have any overlapping intervals (merge overlapping intervals if necessary). -
Return
intervalsafter the insertion. - Example 1:
Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]
- Example 2:
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].
- Constraints:
0 <= intervals.length <= 104intervals[i].length == 20 <= start_i <= end_i <= 105intervals is sorted by start_i in ascending order.newInterval.length == 20 <= start <= end <= 105
- See problem on LeetCode.
Solution: sort first, then compare the start of the current interval with the end of the prior interval
- First, append the new interval to the intervals list, then follow the same idea as Merge Intervals.
class Solution:
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
intervals.append(newInterval)
out = []
for i in sorted(intervals, key=lambda i: i[0]):
# or for i in sorted(intervals, key=lambda i: i.start):
if out and i[0] <= out[-1][1]:
# or if out and i.start <= out[-1].end:
out[-1][1] = max(out[-1][1], i[1])
# or out[-1].end = max(out[-1].end, i.end)
else:
out += i, # Note that "i," is a tuple (because of the comma), and you can extend an iterable to a list (using "+=").
# or out += [i] or simply out.append(i)
return out
Complexity
- Time: \(O(n\log{n} + n) = O(n\log{n})\)
- Space: \(O(n)\)
Solution: makes use of the property that the intervals were initially sorted according to their start times
class Solution:
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
result = []
for interval in intervals:
# the start of the new interval is after the end of the current interval, so we can leave the current interval because the new one does not overlap with it
if newInterval[0] > interval[1]:
result.append(interval)
# the start of the current interval is after the end of the new interval, so we can add the new interval and update it to the current one
elif interval[0] > newInterval[1]:
result.append(newInterval)
newInterval = interval
# the new interval is in the range of the other interval, we have an overlap, so we must choose the min for start and max for end of interval
elif interval[1] >= newInterval[0] or interval[0] <= newInterval[1]:
newInterval[0] = min(interval[0], newInterval[0])
newInterval[1] = max(newInterval[1], interval[1])
result.append(newInterval);
return result
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[62/Medium] Unique Paths
Problem
- There is a robot on an
m x ngrid. The robot is initially located at the top-left corner (i.e.,grid[0][0]). The robot tries to move to the bottom-right corner (i.e.,grid[m - 1][n - 1]). The robot can only move either down or right at any point in time. - Given the two integers
mandn, return the number of possible unique paths that the robot can take to reach the bottom-right corner. -
The test cases are generated so that the answer will be less than or equal to
2 * 10^9. - Example 1:
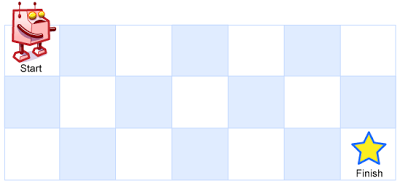
Input: m = 3, n = 7
Output: 28
- Example 2:
Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
- Constraints:
1 <= m, n <= 100
- See problem on LeetCode.
Solution: Recursion
- Since robot can move either down or right, there is only one path to reach the cells in the first row:
right->right->...->right.

- The same is valid for the first column, though the path here is
down->down-> ...->down.

- What about the “inner” cells
(m, n)? To such cell one could move either from the cell on the left(m, n - 1), or from the cell above(m - 1, n). That means that the total number of paths to move into(m, n)cell isuniquePaths(m - 1, n) + uniquePaths(m, n - 1).

class Solution:
def uniquePaths(self, m: int, n: int) -> int:
if m == 1 or n == 1:
return 1
return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)
Solution: Dynamic Programming
- One could rewrite recursive approach into dynamic programming one.
- Algorithm:
- Initiate 2D array
d[m][n] = number of paths. To start, put number of paths equal to 1 for the first row and the first column. For the simplicity, one could initiate the whole 2D array by ones. - Iterate over all “inner” cells:
d[col][row] = d[col - 1][row] + d[col][row - 1]. - Return
d[m - 1][n - 1].
- Initiate 2D array
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
"""
dp[i][j] = number of ways to reach i,j
dp[0][j] = 1, since this is the top row. To reach any element
in the top row, we can only move right, so there is only 1 way.
Similarly, dp[i][0] = 1.
dp[i][j] = num ways to reach one left + num ways to reach one above
= (number of ways to reach i, j-1) + (num ways to reach i-1, j)
= dp[i][j-1] + dp[i-1][j]
"""
d = [[1] * n for _ in range(m)]
for col in range(1, m):
for row in range(1, n):
# The robot can only move either down or right at any point in time.
# so to get to [col][row], you have to look at the previous column (left), i.e., [col - 1][row]
# and the previous row (top), i.e., [col][row - 1]
d[col][row] = d[col - 1][row] + d[col][row - 1]
return d[m - 1][n - 1]
Complexity
- Time: \(\mathcal{O}(n \times m)\)
- Space: \(\mathcal{O}(n \times m)\)
Solution: Combination
-
Could one do better than \(\mathcal{O}(n \times m)\)? The answer is yes.
-
The problem is a classical combinatorial problem: there are \(h + v\) moves to do from start to finish, \(h = m - 1\) horizontal moves, and \(v = n - 1\) vertical ones. One could choose when to move to the right, i.e. to define \(h\) horizontal moves, and that will fix vertical ones. Or, one could choose when to move down, i.e., to define \(v\) vertical moves, and that will fix horizontal ones.

- In other words, we’re asked to compute in how many ways one could choose \(p\) elements from \(p + k\) elements. In mathematics, that’s called binomial coefficients
- The number of horizontal moves to do is \(h = m - 1\), the number of vertical moves is \(v = n - 1\). That results in a simple formula
- The job is done. Now time complexity will depend on the algorithm to compute factorial function \((m + n - 2)!\). In short, standard computation for k!k! using the definition requires \(\mathcal{O}(k^2 \log k)\) time, and that will be not as good as DP algorithm.
- The best known algorithm to compute factorial function is done by Peter Borwein. The idea is to express the factorial as a product of prime powers, so that \(k!\) can be computed in \(\mathcal{O}(k (\log k \log \log k)^2)\) time. That’s better than \(\mathcal{O}(k^2)\) and hence beats DP algorithm.
- The authors prefer not to discuss here various factorial function implementations, and hence provide Python3 solution only, with built-in divide and conquer factorial algorithm. If you’re interested in factorial algorithms, please check out good review on this page.
class Solution:
def combination_solution():
###################################
# Solution 2: combination #
###################################
"""
Answer is (m+n-2) choose (m-1)
Total path length is (m-1) + (n-1).
Consider the list of moves for a single path:
[down, right, down, down, right, ...]
We choose m-1 of these to be down (or choose n-1 of these to be right).
"""
def choose(n, r):
return int(math.factorial(n) / (math.factorial(r) * math.factorial(n-r)))
return choose(m+n-2, m-1)
Complexity
- Time: \(\mathcal{O}((m + n) (\log (m + n) \log \log (m + n))^2)\)
- Space: \(\mathcal{O}(1)\)
[65/Hard] Valid number
Problem
- A valid number can be split up into these components (in order):
- A decimal number or an integer.
- (Optional) An
eorE, followed by an integer.
- A decimal number can be split up into these components (in order):
- (Optional) A sign character (either
+or-). - One of the following formats:
- One or more digits, followed by a dot
.. - One or more digits, followed by a dot
., followed by one or more digits. - A dot
., followed by one or more digits.
- One or more digits, followed by a dot
- (Optional) A sign character (either
- An integer can be split up into these components (in order):
- (Optional) A sign character (either
+or-). - One or more digits.
- (Optional) A sign character (either
- For example, all the following are valid numbers:
["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"], while the following are not valid numbers:["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"]. -
Given a string
s, returntrueifsis a valid number. - Example 1:
Input: s = "0"
Output: true
- Example 2:
Input: s = "e"
Output: false
- Example 3:
Input: s = "."
Output: false
- Constraints:
1 <= s.length <= 20sconsists of only English letters (both uppercase and lowercase), digits (0-9), plus+, minus-, or dot..
- See problem on LeetCode.
Solution
- To solve this problem, we should should just make a list of the possible error conditions and then check for each one.
- The error conditions are:
- More than one exponent character (
e/E), or seeing ane/Ewhen a number has not yet been seen. - More than one sign, or a sign appearing after a decimal or number have been seen. This gets reset when passing an
e/E. - More than one decimal, or a decimal appearing after an
e/Ehas been seen. - Any other non-number character appearing.
- Reaching the end of S without an active number.
- More than one exponent character (
- To help with this process, we can set up some boolean flags for the different things of which we’re keeping track (num, exp, sign, dec). We’ll also need to remember to reset all flags except exp when we find an
e/E, as we’re starting a new integer expression.
Solution: Rule-based
- Method 1:
class Solution:
def isNumber(self, s: str) -> bool:
num, exp, sign, dec = False, False, False, False
for c in s:
if c >= '0' and c <= '9': num = True
elif c == 'e' or c == 'E':
if exp or not num: return False
else: exp, num, sign, dec = True, False, False, False
elif c == '+' or c == '-':
if sign or num or dec: return False
else: sign = True
elif c == '.':
if dec or exp: return False
else: dec = True
else: return False
return num
- Method 2 (check for
seenDigit,seenExponentandseenDot):
class Solution:
def isNumber(self, s: str) -> bool:
seenDigit = seenExponent = seenDot = False
for i, c in enumerate(s):
if c.isdigit():
seenDigit = True
elif c in ["+", "-"]:
if i > 0 and s[i-1] != "e" and s[i-1] != "E":
return False
elif c in ["e", "E"]:
if seenExponent or not seenDigit:
return False
seenExponent = True
seenDigit = False
elif c == ".":
if seenDot or seenExponent:
return False
seenDot = True
else:
return False
return seenDigit
Complexity
- Time: \(O(n)\) where \(n\) is the number of characters in the input string, i.e.,
n = len(s). - Space: \(O(1)\)
Solution: Use a RegEx
class Solution:
def isNumber(self, s: str) -> bool:
# Example: +- 1 or 1. or 1.2 or .2 e or E +- 1
engine = re.compile(r"^[+-]?((\d+\.?\d*)|(\d*\.?\d+))([eE][+-]?\d+)?$")
return engine.match(s.strip(" ")) # i prefer this over putting more things (\S*) in regex
Complexity
- Time: \(O(n)\) where \(n\) is the number of characters in the input string, i.e.,
n = len(s). - Space: \(O(1)\)
[67/Easy] Add Binary
Problem
-
Given two binary strings a and b, return their sum as a binary string.
-
Example 1:
Input: a = "11", b = "1"
Output: "100"
- Example 2:
Input: a = "1010", b = "1011"
Output: "10101"
- Constraints:
1 <= a.length, b.length <= 104a and b consist only of '0' or '1' characters.Each string does not contain leading zeros except for the zero itself.
- See problem on LeetCode.
Solution: Pop digits from each number, add them and do
-
The overall idea is to make up the short two strings with 00 to make the two strings have the same length, and then traverse and calculate from the end to get the final result.
- Let’s understand with an example: Addition of
1and1will lead to carry1and print0, Addition of1and0give us1as carry will lead print0, Addition of last remaining carry1with no body will lead to print1, so, we get something like “1 0 0” as answer -
Since the addition will be
3then print1and carry will remain1. -
Detailed Explanation:
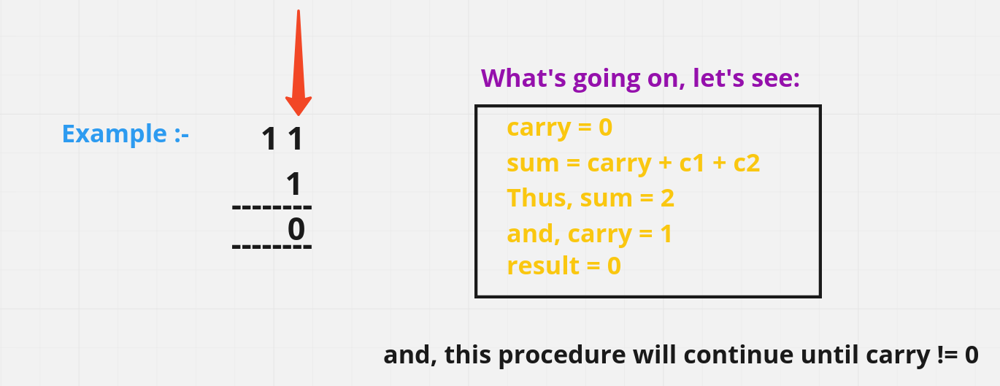
- So, first do we understand how do we perform binary addition. Take an example, given two numbers “11” + “1” where “11” is representing “3” & “1” is “1”, in decimal form. Now let’s perform binary addition it’s very similar to the decimal addition that we do. In decimal what we do we add 2 numbers & if it goes beyond 9 we take a carry. And here also we have a number in range 0 - 1, 2 values over here & in Decimal range is 0 - 9, 10 values are there. So, in binary what it means is if result more than 1, there is a carry otherwise no carry. Let me show you in diagram:
- Per the above diagram, initially
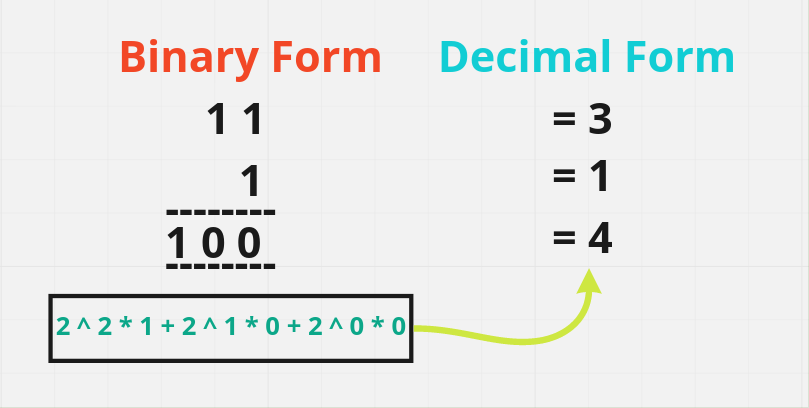
carryis0, then we add1 + 1and get2which is more than1, so there is a carry of1and result is0. Now we have carry of1, again1 + 1is0, and still left with carry of1. And the last carry one will be return as it is. - So, if you see this binary number it is
[2^2 * 1 + 2^1 * 0 + 2^0 * 0]and this is the decimal conversion of[1 0 0]which is4.
class Solution:
def addBinary(self, a: str, b: str) -> str:
# output string
res = ""
# i and j are pointers for string a and b respectively which are used to start adding from right to left
i, j, carry = len(a) - 1, len(b) - 1, 0
while i >= 0 or j >= 0:
sum = carry;
# we subtract by '0' to convert the numbers from a char type into an int, so we can perform operations on the numbers
if i >= 0: sum += ord(a[i]) - ord('0') # ord is use to get the ASCII value of the input character
if j >= 0: sum += ord(b[j]) - ord('0')
i, j = i - 1, j - 1
# obtaining a carry depends on the quotient we get by dividing sum / 2 that will be our carry. Carry could be either 1 or 0.
# if sum is 0, res is 1, then carry would be 0
# if sum is 1, res is 1, then carry would be 0
# if sum is 2, res is 0, then carry would be 1
# if sum is 3, res is 1, then carry would be 1
carry = 1 if sum > 1 else 0
# getting remainder and adding it into our result
res += str(sum % 2)
# add to res until carry becomes 0
if carry != 0 :
res += str(carry)
# you added the bits from R to L, but need the number from L to R
# so reverse the answer and return
return res[::-1]
Complexity
- Time: \(O(max(m, n))\) where \(m\) and \(n\) are the length of strings \(a\) and \(b\)
- Space: \(O(max(m, n))\) due to the
resobject
Solution: Pop digits from each number, add them and add (sum%2) to result and get carry if
class Solution:
def addBinary(self, a: str, b: str) -> str:
carry = 0
result = []
a = list(a)
b = list(b)
while a or b or carry:
if a:
# using pop(), we are reading from the last digit to the first
carry += int(a.pop())
if b:
carry += int(b.pop())
result += str(carry % 2) # result has to be {0, 1}
carry = 1 if carry > 1 else 0 # in-place integer division; can also do "carry //= 2" as above
# you added the bits from R to L, but need the number from L to R
# so reverse the answer and return
return ''.join(result)[::-1]
Complexity
- Time: \(O(max(m, n))\) where \(m\) and \(n\) are the length of strings \(a\) and \(b\)
- Space: \(O(max(m, n))\) due to the
resobject
[87/Hard] Scramble String
Problem
- We can scramble a string
sto get a stringtusing the following algorithm:- If the length of the string is 1, stop.
- If the length of the string is > 1, do the following:
- Split the string into two non-empty substrings at a random index, i.e., if the string is s, divide it to
xandywheres = x + y. - Randomly decide to swap the two substrings or to keep them in the same order. i.e., after this step,
smay becomes = x + yors = y + x. - Apply step 1 recursively on each of the two substrings
xandy.
- Split the string into two non-empty substrings at a random index, i.e., if the string is s, divide it to
-
Given two strings
s1ands2of the same length, return true ifs2is a scrambled string ofs1, otherwise, return false. - Example 1:
Input: s1 = "great", s2 = "rgeat"
Output: true
Explanation: One possible scenario applied on s1 is:
"great" --> "gr/eat" // divide at random index.
"gr/eat" --> "gr/eat" // random decision is not to swap the two substrings and keep them in order.
"gr/eat" --> "g/r / e/at" // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at" --> "r/g / e/at" // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at" --> "r/g / e/ a/t" // again apply the algorithm recursively, divide "at" to "a/t".
"r/g / e/ a/t" --> "r/g / e/ a/t" // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat" which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
- Example 2:
Input: s1 = "abcde", s2 = "caebd"
Output: false
- Example 3:
Input: s1 = "a", s2 = "a"
Output: true
- Constraints:
s1.length == s2.length1 <= s1.length <= 30s1 and s2 consist of lowercase English letters.
- See problem on LeetCode.
Solution: Recursive DP
from collections import Counter
class Solution(object):
def isScramble(self, s1, s2):
if s1 == s2:
return True
if Counter(s1) != Counter(s2):
return False # early backtracking
for i in range(1, len(s1)):
if (self.isScramble(s1[:i], s2[:i]) and self.isScramble(s1[i:], s2[i:])):
return True
if (self.isScramble(s1[:i], s2[-i:]) and self.isScramble(s1[i:], s2[:-i])):
return True
return False
- Same approach; better runtime:
- Basically we try to simulate the construction of the binary tree, and recursively split both
s1ands2into same size every time and check every pair of possible splits until all splits has only one character. - The
sortedis to avoid unnecessary recursions (that grow exponentially), and it turns out to be better thansetandcollections.Counterin terms of runtime.
- Basically we try to simulate the construction of the binary tree, and recursively split both
def isScramble(self, s1: str, s2: str) -> bool:
def split(l1, r1, l2, r2):
if r1 - l1 == 1:
return s1[l1] == s2[l2]
if sorted(s1[l1:r1]) != sorted(s2[l2:r2]):
return False
for i in range(1, r1-l1):
if split(l1, l1+i, l2, l2+i) and split(l1+i, r1, l2+i, r2) or \
split(l1, l1+i, r2-i, r2) and split(l1+i, r1, l2, r2-i):
return True
return split(0, len(s1), 0, len(s2))
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for the recursion call stacks
Solution: Recursive DP with Memoization
class Solution(object):
def __init__(self):
self.dic = {}
def isScramble(self, s1, s2):
if (s1, s2) in self.dic:
return self.dic[(s1, s2)]
if len(s1) != len(s2) or sorted(s1) != sorted(s2): # prunning
self.dic[(s1, s2)] = False
return False
if s1 == s2:
self.dic[(s1, s2)] = True
return True
for i in range(1, len(s1)):
if (self.isScramble(s1[:i], s2[:i]) and self.isScramble(s1[i:], s2[i:])) or \
(self.isScramble(s1[:i], s2[-i:]) and self.isScramble(s1[i:], s2[:-i])):
return True
self.dic[(s1, s2)] = False
return False
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for the recursion call stacks
[88/Easy] Merge Sorted Arrays
Problem
-
You are given two integer arrays
nums1andnums2, sorted in non-decreasing order, and two integersmandn, representing the number of elements innums1andnums2respectively. -
Merge
nums1andnums2into a single array sorted in non-decreasing order. -
The final sorted array should not be returned by the function, but instead be stored inside the array
nums1. To accommodate this,nums1has a length ofm + n, where the firstmelements denote the elements that should be merged, and the lastnelements are set to 0 and should be ignored. nums2 has a length ofn. -
Example 1:
Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]
Explanation: The arrays we are merging are [1,2,3] and [2,5,6].
The result of the merge is [1,2,2,3,5,6] with the underlined elements coming from nums1.
- Example 2:
Input: nums1 = [1], m = 1, nums2 = [], n = 0
Output: [1]
Explanation: The arrays we are merging are [1] and [].
The result of the merge is [1].
- Example 3:
Input: nums1 = [0], m = 0, nums2 = [1], n = 1
Output: [1]
Explanation: The arrays we are merging are [] and [1].
The result of the merge is [1].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
- Constraints:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
-
Follow up: Can you come up with an algorithm that runs in
O(m + n)time? - See problem on LeetCode.
Solution: Start at the end of both arrays, get bigger element
class Solution(object):
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
while m > 0 and n > 0:
# Start at the end of both arrays and get the bigger element.
if nums1[m - 1] > nums2[n - 1]:
nums1[m + n - 1] = nums1[m - 1]
m -= 1
else:
nums1[m + n - 1] = nums2[n - 1]
n -= 1
nums1[:n] = nums2[:n] # while n > 0:
# nums1[n-1] = nums2[n-1]
# n -= 1
Complexity
- Time: \(O(m + n + n) = O(m + n)\)
- Space: \(O(1)\) since nothing new is created (the result is calculated in-place).
[100/Easy] Same Tree
Problem
-
Given the roots of two binary trees
pandq, write a function to check if they are the same or not. -
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
-
Example 1:
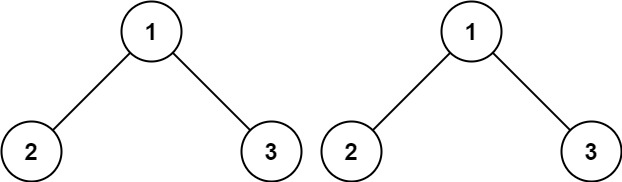
Input: p = [1,2,3], q = [1,2,3]
Output: true
- Example 2:
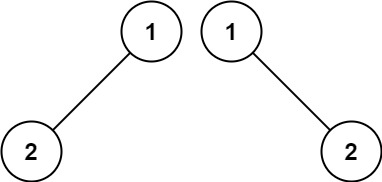
Input: p = [1,2], q = [1,null,2]
Output: false
- Example 3:
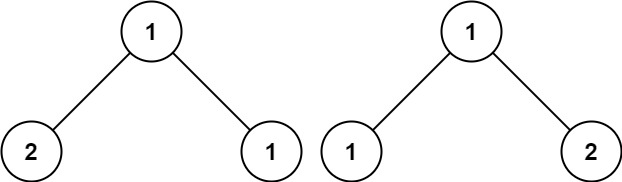
Input: p = [1,2,1], q = [1,1,2]
Output: false
- Constraints:
The number of nodes in both trees is in the range [0, 100].-104 <= Node.val <= 104
- See problem on LeetCode.
Solution: Iterative DFS with Deque
- Iteration is actually better than recursion in best case scenario, as it stops checking the tree whenever it finds the first mismatching node, but note that in Big O notation they are the same.
from collections import deque
class Solution:
def isSameTree(self, p, q):
"""
:type p: TreeNode
:type q: TreeNode
:rtype: bool
"""
def check(p, q):
# if both are None
if not p and not q:
return True
# one of p and q is None
if not q or not p:
return False
if p.val != q.val:
return False
return True
deq = deque([(p, q),])
while deq:
p, q = deq.popleft()
if not check(p, q):
return False
if p:
deq.append((p.left, q.left))
deq.append((p.right, q.right))
return True
Solution: Pre-order Recursive DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
# base case: check whether both nodes are null, if so return true.
if not p and not q:
return True
# base case: if one node is null and the other isn't, the trees can't be the same.
# note that if you've reached here both p and q can't be null (because of the if condition above)
# but one can be null.
if not q or not p: # or if not q and p or q and not p:
return False
# base case: if the node values differ, return false.
if p.val != q.val:
return False
# normal case
return self.isSameTree(p.right, q.right) and self.isSameTree(p.left, q.left)
Complexity
- Time: \(O(n)\) where \(n\) is the number of nodes in the binary tree
- Space: \(O(1)\)
[114/Medium] Flatten Binary Tree to Linked List
Problem
-
Given the
rootof a binary tree, flatten the tree into a “linked list”:- The “linked list” should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
- The “linked list” should be in the same order as a pre-order traversal of the binary tree.
-
Example 1:
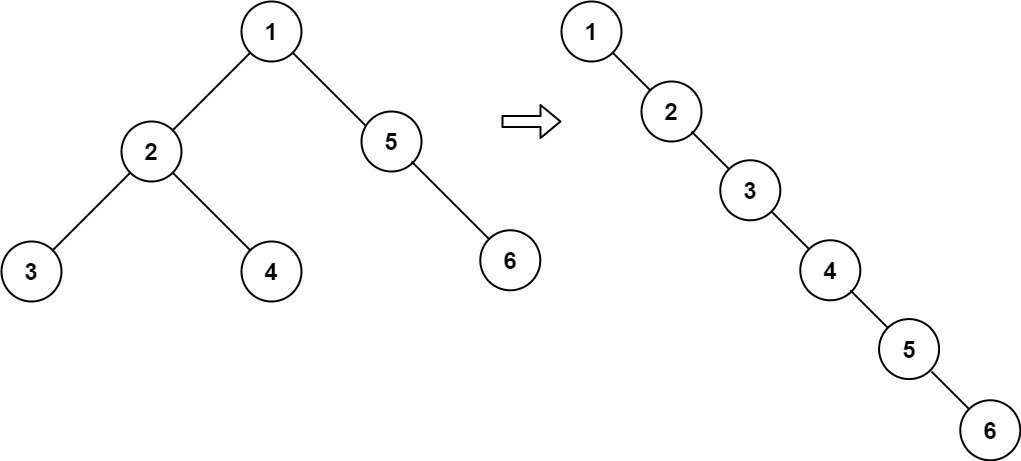
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]
- Example 2:
Input: root = []
Output: []
- Example 3:
Input: root = [0]
Output: [0]
- Constraints:
The number of nodes in the tree is in the range [0, 2000].-0 -100 <= Node.val <= 100
- See problem on LeetCode.
Solution: Morris Traversal
-
There is actually a way to traverse a binary tree with a space complexity of
O(1)while staying at a time complexity ofO(N), though it does require modifying the tree’s structure. In this problem that’s specifically being called for, so it’s a valid approach, though it won’t always be appropriate to modify the source binary tree in other situations. -
The approach is called the Morris traversal. At its heart, it takes advantage of the basic nature of ordered traversals to iterate through and unwind the tree. In a pre-order traversal of a binary tree, each vertex is processed in (
node, left, right) order. This means that the entire left subtree could be placed between the node and its right subtree. -
To do this, however, we’ll first have to locate the last node in the left subtree. This is easy enough, since we know that the last node of a pre-order tree can be found by moving right as many times as possible from its root.
-
So we should be able to move through the binary tree, keeping track of the curent node (
curr). Whenever we find a left subtree, we can dispatch arunnerto find its last node, then stitch together both ends of the left subtree into the right path ofcurr, taking heed to sever the left connection at curr. -
Once that’s done, we can continue to move
currto the right, looking for the next left subtree. Whencurrcan no longer move right, the tree will be successfully flattened.

class Solution:
def flatten(self, root: TreeNode) -> None:
curr = root
while curr:
if curr.left:
runner = curr.left
while runner.right: runner = runner.right
runner.right, curr.right, curr.left = curr.right, curr.left, None
curr = curr.right
Complexity
- Time: \(O(n)\) where \(n\) is the number of nodes in the binary tree
- Space: \(O(1)\)
Solution: \(O(1)\) Space
-
In order to properly connect the linked list, we’ll need to start at the bottom and work up. This means that we’ll need to move in reverse pre-order traversal order through the binary tree. Since pre-order traversal is normally “
node, left, right”, we’ll have to move in the reverse order of “right, left, node”. -
In order to complete this solution in \(O(1)\) space, we won’t be able to conveniently backtrack via a stack, so the key to this solution will be to retreat all the way back up to the root each time we reach a leaf. This will push the time complexity to \(O(n^2)\).
-
We’ll want to first set up head and
currto keep track of the head of the linked list we’re building and the current node we’re visiting. We’ll know we’re finished once head = root. -
To follow the reverse pre-order traversal order, we’ll first attempt to go right and then left. Since we’re backtracking to root, however, we’ll eventually run back into the same node that we’ve set as head doing this. To prevent this, we’ll stop before moving to the head node and sever the connection.
-
Now that we can’t run into already-completed territory, we can be confident that any leaf we move to must be the next value for head, so we should connect it to the old head, update head, and reset back to the root.
-
As noted before, once
head = root, we’ve finished our traversal and can exit the function.
class Solution:
def flatten(self, root: TreeNode) -> None:
head, curr = None, root
while head != root:
if curr.right == head: curr.right = None
if curr.left == head: curr.left = None
if curr.right: curr = curr.right
elif curr.left: curr = curr.left
else: curr.right, head, curr = head, curr, root
Complexity
- Time: \(O(n^2)\) where \(n\) is the number of nodes in the binary tree, due to repeated backtracking to root
- Space: \(O(1)\)
Solution: Recursive reversed preorder traversal
- The trick is to consider the order of the traversal – traverse the graph in reverse preorder: (
right, left, node). At any given node, solve the right subtree first. At the end of the right subtree,self.prevpoints to the start of the right part. Then solve the left subtree. Notice that at the beginning of the left part,self.prevstill points to the start of the right part. Finally when the left part is done,self.prevpoints to the start of the left part. - Finally, return the top of the computed solution, which is done using the last three lines. The next node to left-append to the computed solution is the root. First, after
root, comesself.prev. Second,root.left= None, which is straightforward. Finally,self.previs set toroot, becauseself.prevholds the top of the computed tree up to this point.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def __init__(self):
self.prev = None
def flatten(self, root: Optional[TreeNode]) -> None:
if not root:
return None
self.flatten(root.right)
self.flatten(root.left)
root.right = self.prev
root.left = None
self.prev = root
-
Walkthrough:
root / 1 / \ 3 4- Let’s see what is happening with this code.
- Step 1:
Node(4).right = NoneNode(4).left = Noneprev = Node(4)
- Step 2:
Node(3).right = Node(4) (prev)Node(3).left = Noneprev = Node(3)->Node(4)
- Step 3:
Node(1).right = prev = Node(3) -> Node(4)Node(1).left = Noneprev = Node(1)->Node(3)->Node(4) (which is the answer)
- The answer use self.prev to recode the ordered tree of the right part of current node.
- Remove the left part of current node.
- Step 1:
- Let’s see what is happening with this code.
-
Same approach; rehashed:
-
In order to properly connect the linked list, we’ll need to start at the bottom and work up. This means that we’ll need to move in reverse pre-order traversal order through the binary tree. Since pre-order traversal is normally “node, left, right”, we’ll have to move in the reverse order of “right, left, node”.
-
Binary tree traversal is prime ground for a recursive solution, so let’s define a helper (
revPreOrder) for the purpose. We’ll also keep a global variableheadto keep track of the head of the linked list as we work our way backwards. -
Per our reverse pre-order traversal approach, we want to recursively work down the right path first then the left path, if they exist. Once we’ve flattened the left and right paths recursively,
headshould at this point be equal to the next node after the current one, so we should set it asnode.right. We shouldn’t forget to setnode.lefttoNone, as well. -
Once we’re done with the current node, we can update
headtonodeand allow the recursion to complete and move back up to the next layer. Once the recursion stack is exhausted,headwill be equal torootagain. -
Lastly, we have to deal with an edge case of an empty root, so we can just make sure to only call the initial recursion on
rootifrootactually is a node. There is no need for a return statement ifrootisNone, because the absence of one will returnNoneautomatically to make the test suite happy.
-
class Solution:
head = None
def flatten(self, root: TreeNode) -> None:
def revPreOrder(node: TreeNode) -> None:
if node.right: revPreOrder(node.right)
if node.left: revPreOrder(node.left)
node.left, node.right, self.head = None, self.head, node
# note that there is no need for a return statement if `root` is `None`,
# because the absence of one will return `None` automatically to make the test suite happy
if root:
revPreOrder(root)
Complexity
- Time: \(O(n)\) where \(n\) is the number of nodes in the binary tree
- Space: \(O(n)\) for the recursion stack, which is as long as the maximum depth of the binary tree, which can go up to \(n\)
[134/Medium] Gas Station
Problem
-
There are
ngas stations along a circular route, where the amount of gas at thei-thstation isgas[i]. -
You have a car with an unlimited gas tank and it costs
cost[i]of gas to travel from thei-thstation to its next(i + 1)-thstation. You begin the journey with an empty tank at one of the gas stations. -
Given two integer arrays
gasandcost, return the starting gas station’s index if you can travel around the circuit once in the clockwise direction, otherwise return-1. If there exists a solution, it is guaranteed to be unique -
Example 1:
Input: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
Output: 3
Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
- Example 2:
Input: gas = [2,3,4], cost = [3,4,3]
Output: -1
Explanation:
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
- Constraints:
n == gas.length == cost.length1 <= n <= 1050 <= gas[i], cost[i] <= 104
- See problem on LeetCode.
Solution: One loop
- Intuition:
- The first idea is to check every single station:
- Choose the station as starting point.
- Perform the road trip and check how much gas we have in tank at each station.
- That means \(\mathcal{O}(N^2)\) time complexity, and for sure one could do better.
- The first idea is to check every single station:
- Let’s notice two things.
- It’s impossible to perform the road trip if
sum(gas) < sum(cost). In this situation the answer is-1.

-
One could compute total amount of gas in the tank
total_tank = sum(gas) - sum(cost)during the round trip, and then return-1if total_tank< 0. -
It’s impossible to start at a station
iifgas[i] - cost[i] < 0, because then there is not enough gas in the tank to travel toi + 1station.
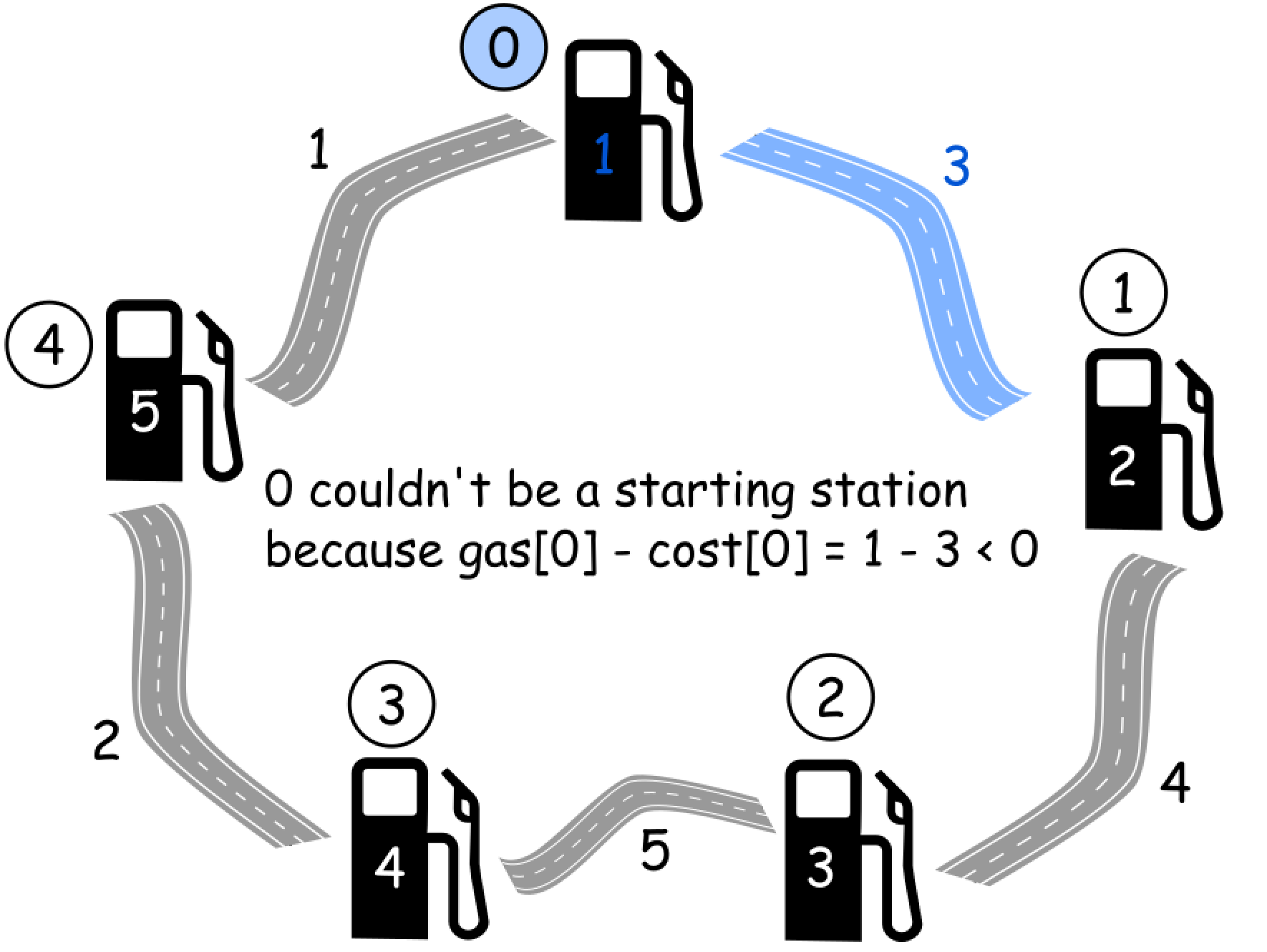
- The second fact could be generalized. Let’s introduce
curr_tankvariable to track the current amount of gas in the tank. If at some stationcurr_tankis less than0, that means that one couldn’t reach this station. - Next step is to mark this station as a new starting point, and reset
curr_tankto zero since one starts with no gas in the tank.
- It’s impossible to perform the road trip if
- Algorithm:
- Now the algorithm is straightforward:
- Initiate
total_tankandcurr_tankas zero, and choose station0as a starting station. - Iterate over all stations:
- Update
total_tankandcurr_tankat each step, by addinggas[i]and subtractingcost[i]. - If
curr_tank < 0ati + 1station, makei + 1station a new starting point and resetcurr_tank = 0to start with an empty tank.
- Update
- Return
-1iftotal_tank < 0and starting station otherwise.
- Initiate
- Now the algorithm is straightforward:
class Solution:
def canCompleteCircuit(self, gas, cost):
"""
:type gas: List[int]
:type cost: List[int]
:rtype: int
"""
n = len(gas)
total_tank, curr_tank = 0, 0
starting_station = 0
for i in range(n):
total_tank += gas[i] - cost[i]
curr_tank += gas[i] - cost[i]
# If one couldn't get here,
if curr_tank < 0:
# Pick up the next station as the starting one.
starting_station = i + 1
# Start with an empty tank.
curr_tank = 0
return starting_station if total_tank >= 0 else -1
Complexity
- Time: \(O(n)\) since there is only one loop over all stations here.
- Space: \(O(1)\) since it’s a constant space solution.
[138/Medium] Copy List with Random Pointer
Problem
-
A linked list of length
nis given such that each node contains an additional random pointer, which could point to any node in the list, ornull. -
Construct a deep copy of the list. The deep copy should consist of exactly
nbrand new nodes, where each new node has its value set to the value of its corresponding original node. Both thenextandrandompointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list. -
For example, if there are two nodes
XandYin the original list, whereX.random --> Y, then for the corresponding two nodesxandyin the copied list,x.random --> y. -
Return the head of the copied linked list.
- The linked list is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:
val: an integer representingNode.valrandom_index: the index of the node (range from0ton-1) that therandompointer points to, ornullif it does not point to any node.
-
Your code will only be given the
headof the original linked list. - Example 1:
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]
- Example 2:
Input: head = [[1,1],[2,1]]
Output: [[1,1],[2,1]]
- Example 3:
Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]
- Constraints:
0 <= n <= 1000-104 <= Node.val <= 104- Node.random is null or is pointing to some node in the linked list.
- See problem on LeetCode.
Solution: Two loops
- The first
whileloop builds the mapping of the original object to its copy while the second loop, we basically connect stuff, i.e.,nextandrandomusing the mapping:
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
# build mapping of original node to it's copy
current = head
mapping = {}
while current:
mapping[current] = Node(current.val)
current = current.next
# now that we have the complete mapping, we can use it to
# construct the linked list copy
current = head
while current:
# we have all the copy nodes but they aren't connected i.e. the next
# & random all point to None. let's connect them here. it's easy
# since we have a complete node-to-copy mapping
if current.next:
mapping[current].next = mapping[current.next]
if current.random:
mapping[current].random = mapping[current.random]
current = current.next
# return the head of the linked list copy
return mapping[head]
Complexity
- Time: \(O(n + n) = O(n)\)
- Space: \(O(n)\)
Solution: Recursion
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
def copyRandomList(self, head: 'Optional[Node]', seen={None: None}) -> 'Optional[Node]':
# Node could have been seen earlier through either random or next pointers
if head not in seen:
seen[head] = Node(head.val)
seen[head].next = self.copyRandomList(head.next, seen)
seen[head].random = self.copyRandomList(head.random, seen)
return seen[head]
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[143/Medium] Reorder List
- You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> … -> Ln - 1 -> Ln
- Reorder the list to be on the following form:
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
-
You may not modify the values in the list’s nodes. Only nodes themselves may be changed.
-
Example 1:
Input: head = [1,2,3,4]
Output: [1,4,2,3]
- Example 2:
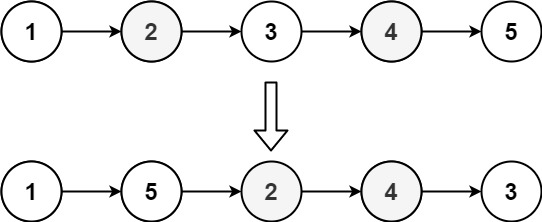
Input: head = [1,2,3,4,5]
Output: [1,5,2,4,3]
- Constraints:
The number of nodes in the list is in the range [1, 5 * 104].1 <= Node.val <= 1000
- See problem on LeetCode.
Solution: Find middle; reverse linked list; merged sorted linked lists
-
This problem is a combination of these three easy problems:
- Middle of the Linked List.
- Reverse Linked List.
- Merge Two Sorted Lists.
-
Overview:
- Find a middle node of the linked list. If there are two middle nodes, return the second middle node. Example: for the list
1->2->3->4->5->6, the middle element is4. - Once a middle node has been found, reverse the second part of the list. Example: convert
1->2->3->4->5->6into1->2->3and6->5->4. - Now merge the two sorted lists. Example: merge
1->2->3->4and6->5->4into1->6->2->5->3->4.
- Find a middle node of the linked list. If there are two middle nodes, return the second middle node. Example: for the list
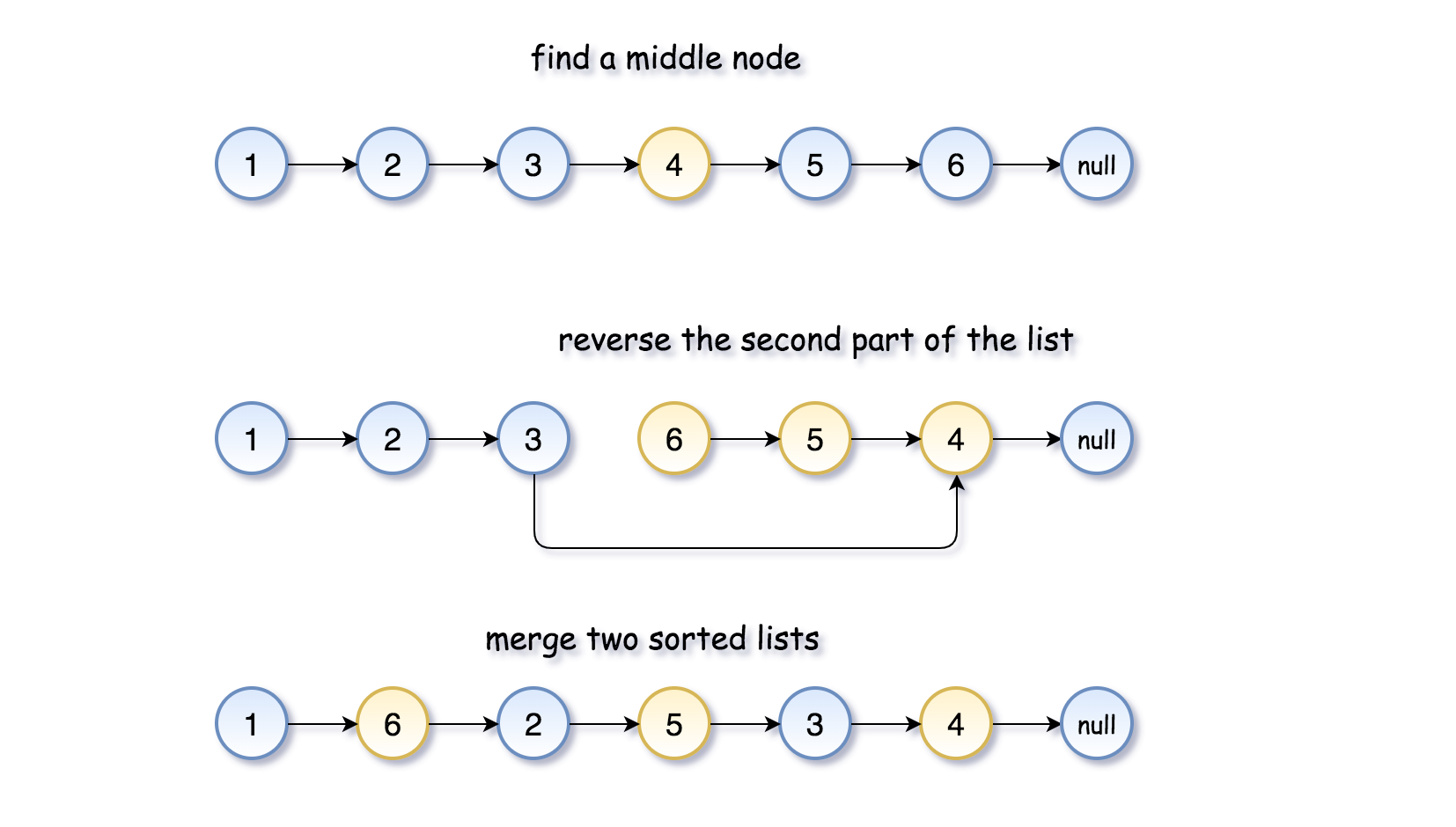
-
Now let’s check each algorithm part in more detail.
-
Find a Middle Node:
- Let’s use two pointers, slow and fast. While the slow pointer moves one step forward
slow = slow.next, the fast pointer moves two steps forwardfast = fast.next.next, i.e., fast traverses twice as fast as slow. When the fast pointer reaches the end of the list, the slow pointer should be in the middle.
- Let’s use two pointers, slow and fast. While the slow pointer moves one step forward
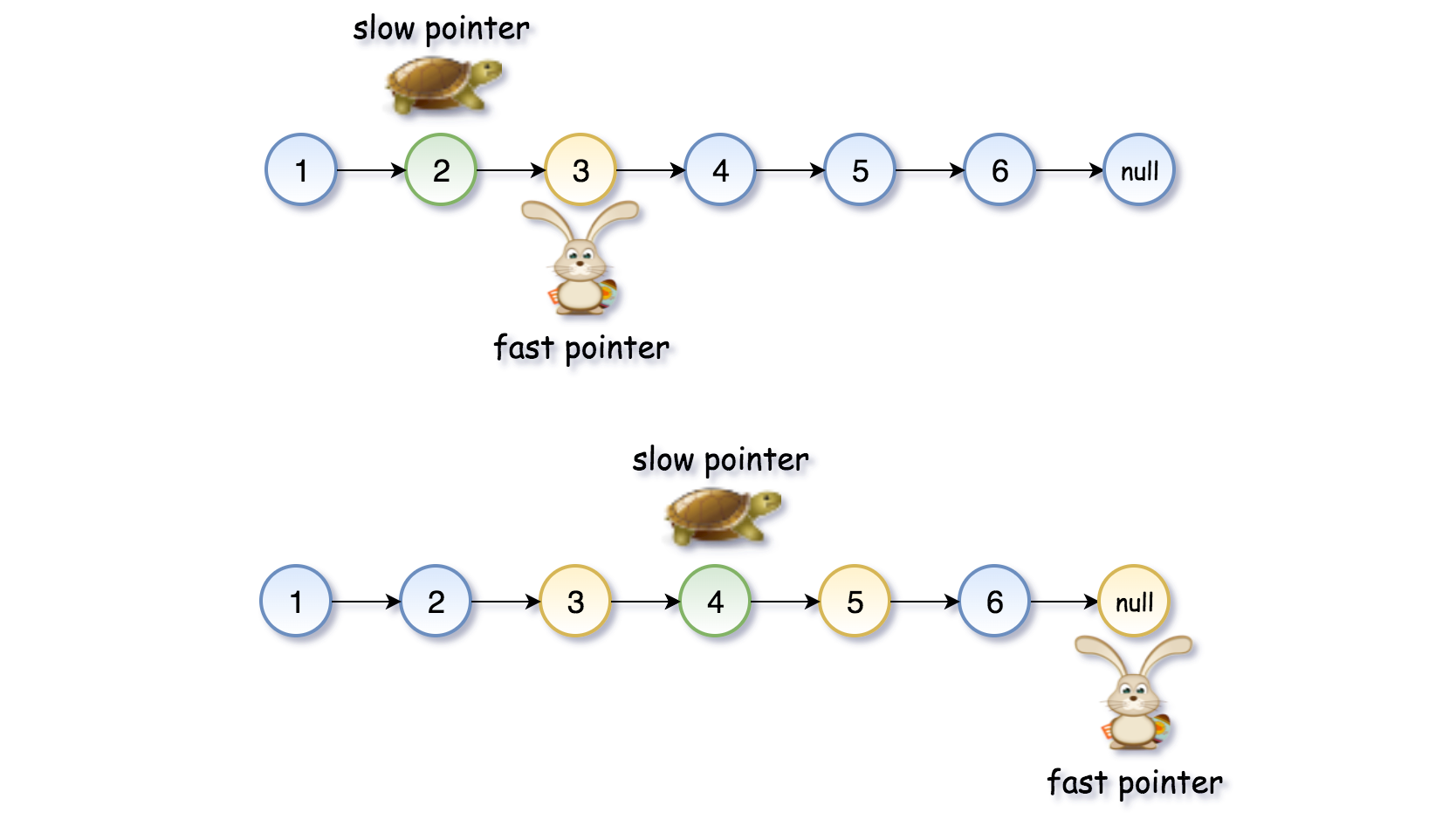
# find the middle of linked list [Problem 876]
# in 1->2->3->4->5->6 find 4
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
- Reverse the Second Part of the List:
- Let’s traverse the list starting from the middle node
slowand its virtual predecessorNone. For each current node, save its neighbors: the previous nodeprevand the next nodetmp = curr.next. - While you’re moving along the list, change the node’s next pointer to point to the previous node:
curr.next = prev, and shift the current node to the right for the next iteration:prev = curr, curr = tmp.
- Let’s traverse the list starting from the middle node
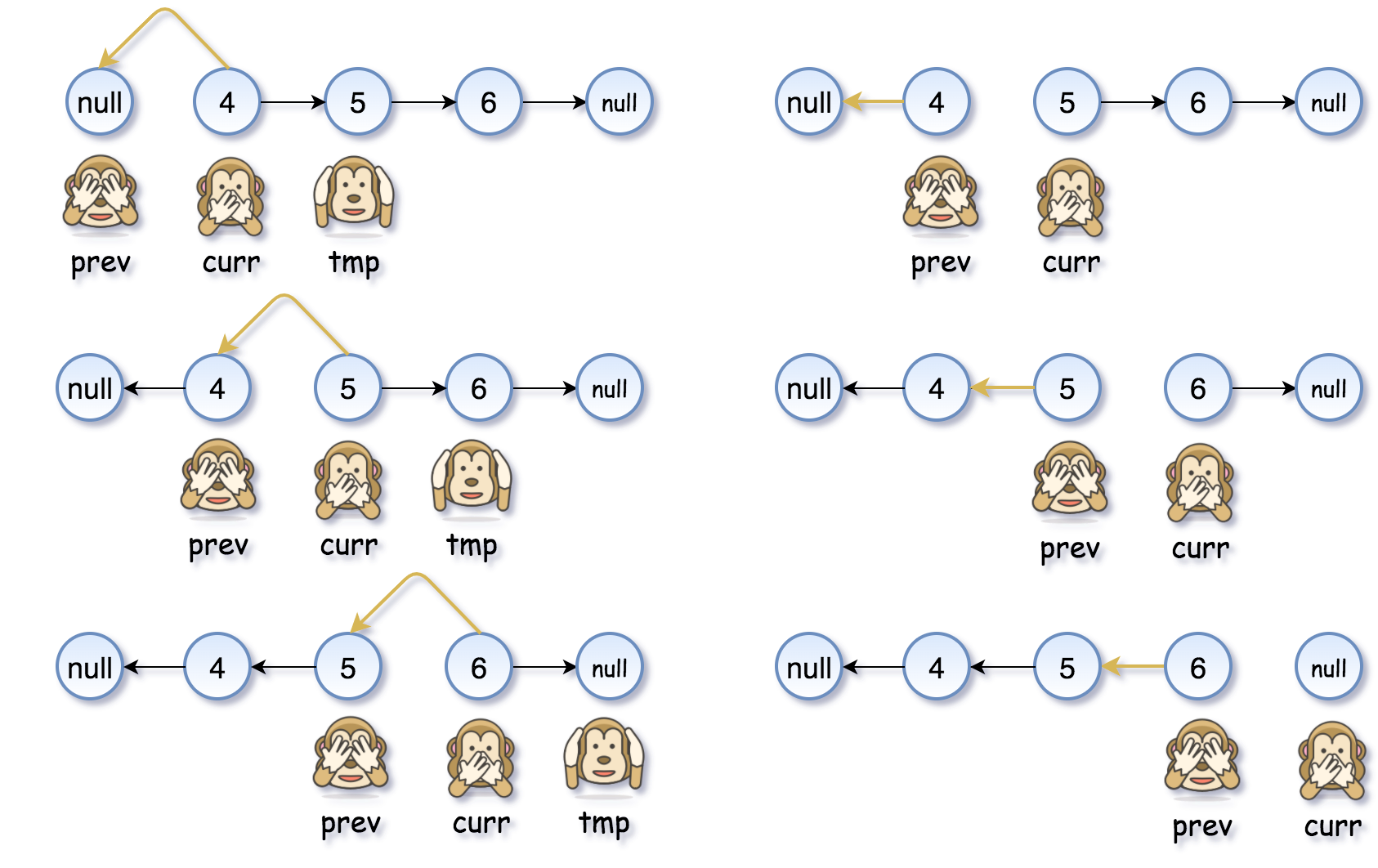
# reverse the second part of the list [Problem 206]
# convert 1->2->3->4->5->6 into 1->2->3->4 and 6->5->4
# reverse the second half in-place
prev, curr = None, slow
while curr:
tmp = curr.next
curr.next = prev
prev = curr
curr = tmp
- There is a more elegant way to do it in Python (without using a temp variable):
# reverse the second part of the list [Problem 206]
# convert 1->2->3->4->5->6 into 1->2->3->4 and 6->5->4
# reverse the second half in-place
prev, curr = None, slow
while curr:
curr.next, prev, curr = prev, curr, curr.next
-
Merge Two Sorted Lists:
-
This algorithm is similar to the one for list reversal.
-
Let’s pick the first node of each list -
firstandsecond, and save their successors. While you’re traversing the list, set the first node’s next pointer to point to the second node, and the second node’s next pointer to point to the successor of the first node. For this iteration the job is done, and for the next iteration move to the previously saved nodes’ successors.
-
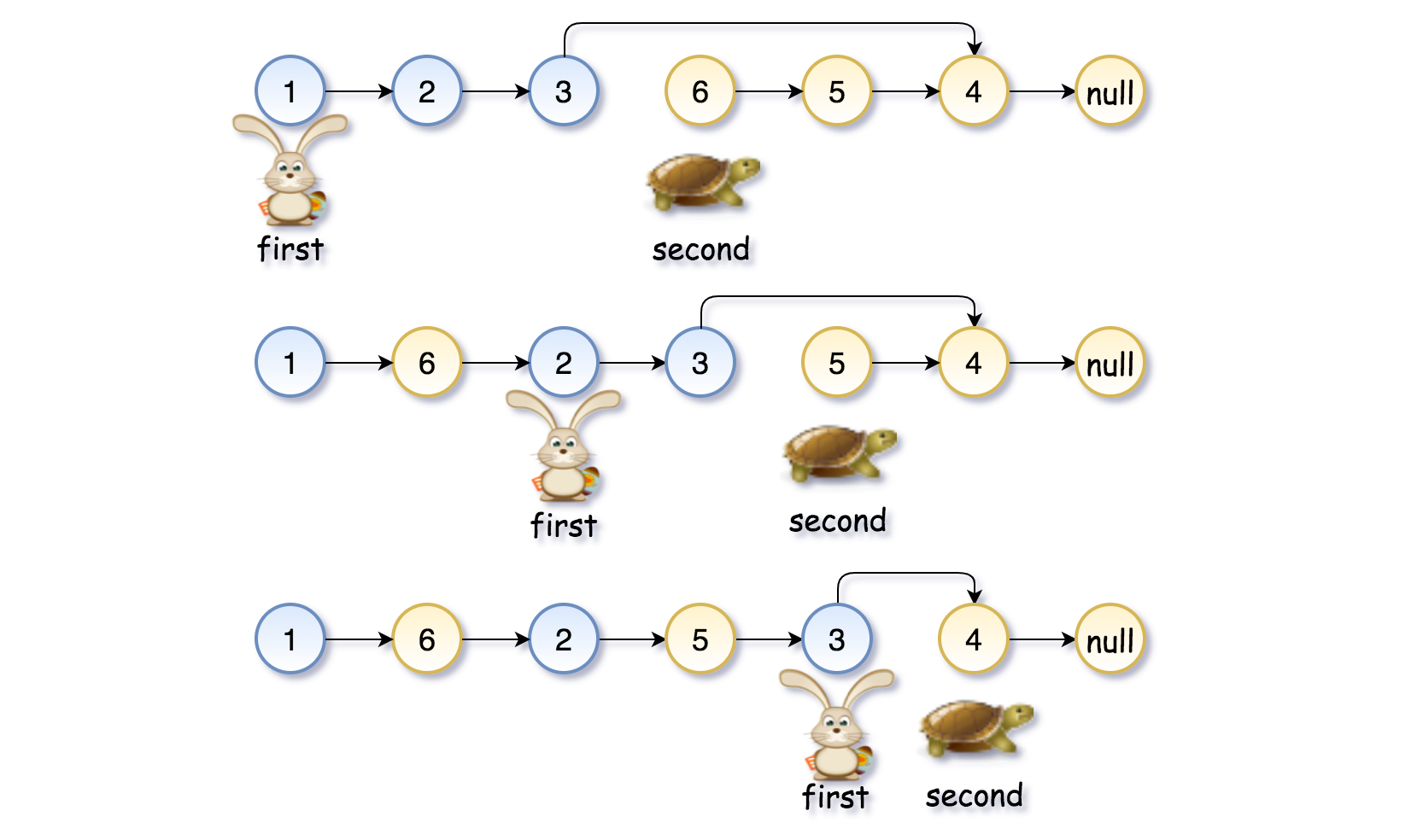
# merge two sorted linked lists [Problem 21]
# merge 1->2->3->4 and 6->5->4 into 1->6->2->5->3->4
first, second = head, prev
while second.next:
tmp = first.next
first.next = second
first = tmp
tmp = second.next
second.next = first
second = tmp
- Once again, there is a way to make things simple in Python (without using a temp variable):
# merge two sorted linked lists [Problem 21]
# merge 1->2->3->4 and 6->5->4 into 1->6->2->5->3->4
first, second = head, prev
while second.next:
first.next, first = second, first.next
second.next, second = first, second.next
- Implementation:
- Now it’s time to put all the pieces together.
class Solution:
def reorderList(self, head: ListNode) -> None:
if not head:
return
# find the middle of linked list [Problem 876]
# in 1->2->3->4->5->6 find 4
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# reverse the second part of the list [Problem 206]
# convert 1->2->3->4->5->6 into 1->2->3->4 and 6->5->4
# reverse the second half in-place
prev, curr = None, slow
while curr:
curr.next, prev, curr = prev, curr, curr.next
# merge two sorted linked lists [Problem 21]
# merge 1->2->3->4 and 6->5->4 into 1->6->2->5->3->4
first, second = head, prev
while second.next:
first.next, first = second, first.next
second.next, second = first, second.next
- Similar approach; using functions for each of the three sub-tasks:
class Solution:
def reorderList(self, head: ListNode) -> None:
def findMid(head: ListNode) -> ListNode:
prev = None
slow = head
fast = head
while fast and fast.next:
prev = slow
slow = slow.next
fast = fast.next.next
prev.next = None
return slow
def reverse(head: ListNode) -> ListNode:
prev = None
curr = head
while curr:
next = curr.next
curr.next = prev
prev = curr
curr = next
return prev
def merge(l1: ListNode, l2: ListNode) -> None:
while l2:
next = l1.next
l1.next = l2
l1 = l2
l2 = next
if not head
return
if not head.next:
return head
mid = findMid(head)
reversed = reverse(mid)
merge(head, reversed)
Complexity
- Time: \(O(n)\). There are three steps here. To identify the middle node takes \(\mathcal{O}(N)\) time. To reverse the second part of the list, one needs \(N/2\) operations. The final step, to merge two lists, requires \(N/2\) operations as well. In total, that results in \(\mathcal{O}(N)\) time complexity.
- Space: \(O(1)\), since we do not allocate any additional data structures.
[148/Medium] Sort List
-
Given the
headof a linked list, return the list after sorting it in ascending order. -
Example 1:
Input: head = [4,2,1,3]
Output: [1,2,3,4]
- Example 2:
Input: head = [-1,5,3,4,0]
Output: [-1,0,3,4,5]
- Example 3:
Input: head = []
Output: []
- Constraints:
The number of nodes in the list is in the range [0, 5 * 10^4].-10^5 <= Node.val <= 10^5
-
Follow up: Can you sort the linked list in \(O(n\log{n})\) time and \(O(1)\) memory (i.e. constant space)?
- See problem on LeetCode.
Solution: Merge Sort / Divide-and-Conquer
class Solution:
def sortList(self, head: ListNode) -> ListNode:
def merge( a, b):
if not a:
return b
elif not b:
return a
if a.val < b.val:
a.next = merge(a.next, b)
return a
else:
b.next = merge(a, b.next)
return b
## base case
if head is None:
# empty node
return None
elif head.next is None:
# one node only
return head
## general case
# divide into two halves
pre, slow, fast = None, head, head
while fast and fast.next:
pre, slow, fast = slow, slow.next, fast.next.next
pre.next = None
# sort by divide-and-conquer
first_half = self.sortList(head)
second_half = self.sortList(slow)
result = merge(first_half, second_half)
return result
Complexity
- Time: \(O(n\log{n})\)
- Space: \(O(1)\)
[158/Hard] Read N Characters Given read4 II - Call Multiple Times
-
Given a
fileand assume that you can only read the file using a given methodread4, implement a methodreadto readncharacters. Your methodreadmay be called multiple times. -
Method
read4:-
The API
read4reads four consecutive characters from file, then writes those characters into the buffer arraybuf4. -
The return value is the number of actual characters read.
-
Note that
read4()has its own file pointer, much like FILE *fp in C.
-
-
Definition of
read4:
Parameter: char[] buf4
Returns: int
buf4[] is a destination, not a source. The results from read4 will be copied to buf4[].
- Below is a high-level example of how read4 works:
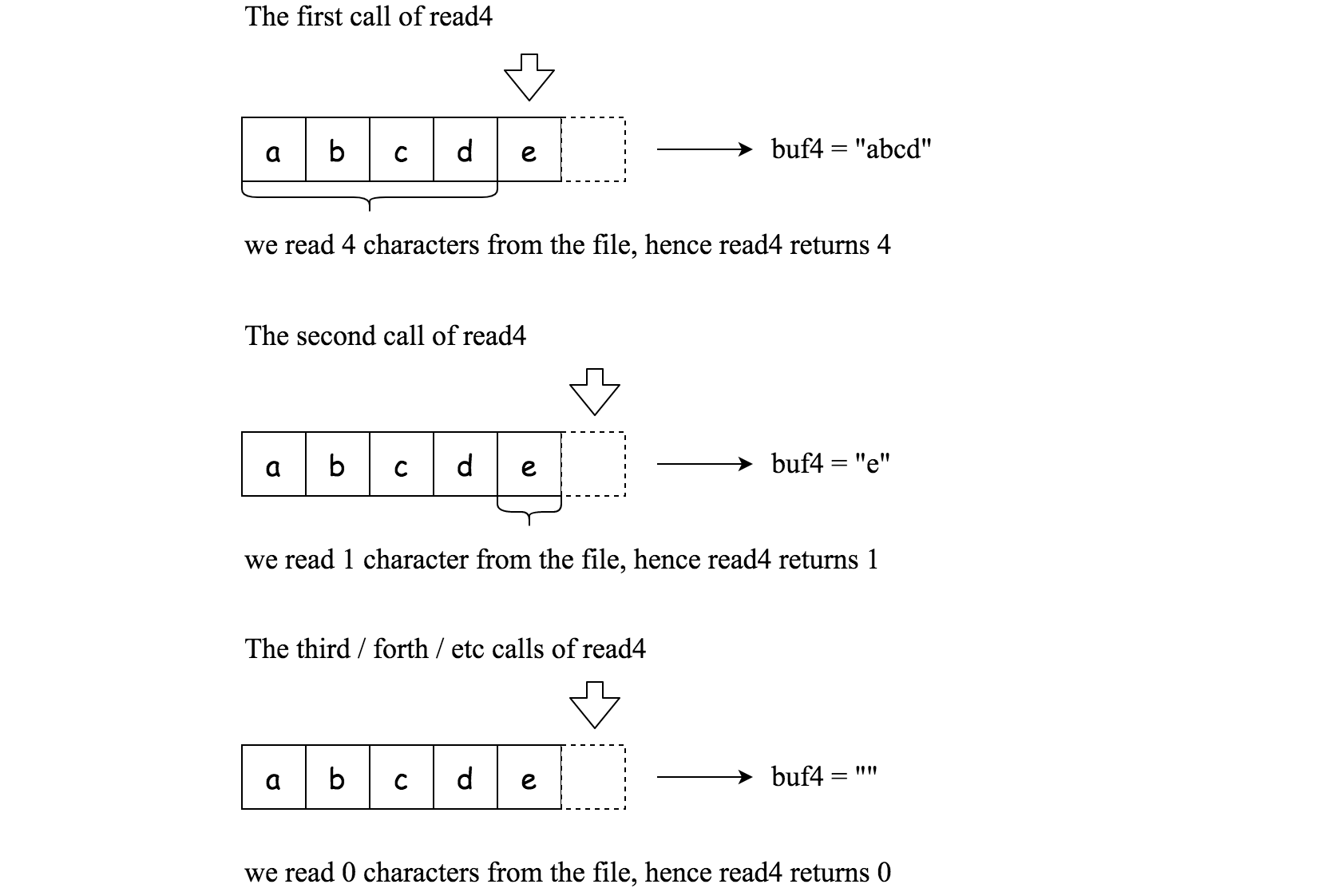
File file("abcde"); // File is "abcde", initially file pointer (fp) points to 'a'
char[] buf4 = new char[4]; // Create buffer with enough space to store characters
read4(buf4); // read4 returns 4. Now buf4 = "abcd", fp points to 'e'
read4(buf4); // read4 returns 1. Now buf4 = "e", fp points to end of file
read4(buf4); // read4 returns 0. Now buf4 = "", fp points to end of file
-
Method
read: -
By using the
read4method, implement the method read that reads n characters from file and store it in the buffer arraybuf. Consider that you cannot manipulate file directly. -
The return value is the number of actual characters read.
-
Definition of
read:
Parameters: char[] buf, int n
Returns: int
buf[] is a destination, not a source. You will need to write the results to buf[].
- Note:
Consider that you cannot manipulate the file directly. The file is only accessible for read4 but not for read.The read function may be called multiple times.Please remember to RESET your class variables declared in Solution, as static/class variables are persisted across multiple test cases. Please see here for more details.You may assume the destination buffer array, buf, is guaranteed to have enough space for storing n characters.It is guaranteed that in a given test case the same buffer buf is called by read.
- Example 1:
Input: file = "abc", queries = [1,2,1]
Output: [1,2,0]
Explanation: The test case represents the following scenario:
File file("abc");
Solution sol;
sol.read(buf, 1); // After calling your read method, buf should contain "a". We read a total of 1 character from the file, so return 1.
sol.read(buf, 2); // Now buf should contain "bc". We read a total of 2 characters from the file, so return 2.
sol.read(buf, 1); // We have reached the end of file, no more characters can be read. So return 0.
Assume buf is allocated and guaranteed to have enough space for storing all characters from the file.
- Example 2:
Input: file = "abc", queries = [4,1]
Output: [3,0]
Explanation: The test case represents the following scenario:
File file("abc");
Solution sol;
sol.read(buf, 4); // After calling your read method, buf should contain "abc". We read a total of 3 characters from the file, so return 3.
sol.read(buf, 1); // We have reached the end of file, no more characters can be read. So return 0.
- Constraints:
1 <= file.length <= 500file consist of English letters and digits.1 <= queries.length <= 101 <= queries[i] <= 500
- See problem on LeetCode.
Solution: Queue
class Solution:
# @param buf, Destination buffer (a list of characters)
# @param n, Maximum number of characters to read (an integer)
# @return The number of characters read (an integer)
def __init__(self):
self.queue = []
def read(self, buf, n):
idx = 0
while True:
buf4 = [""]*4
l = read4(buf4)
self.queue.extend(buf4)
curr = min(len(self.queue), n-idx)
for i in xrange(curr):
buf[idx] = self.queue.pop(0)
idx += 1
if curr == 0:
break
return idx
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[203/Easy] Remove Linked List Elements
Problem
-
Given the
headof a linked list and an integer val, remove all the nodes of the linked list that hasNode.val == val, and return the new head. -
Example 1:
Input: head = [1,2,6,3,4,5,6], val = 6
Output: [1,2,3,4,5]
- Example 2:
Input: head = [], val = 1
Output: []
- Example 3:
Input: head = [7,7,7,7], val = 7
Output: []
- Constraints:
The number of nodes in the list is in the range [0, 104].1 <= Node.val <= 500 <= val <= 50
- See problem on LeetCode.
Solution: Iteration
- Edge cases:
- The linked list is empty, i.e., the head node is
None. - Multiple nodes with the target value in a row.
- The head node has the target value.
- The head node, and any number of nodes immediately after it have the target value.
- All of the nodes have the target value.
- The last node has the target value.
- The linked list is empty, i.e., the head node is
- First we remove all (if any) target nodes from the beginning (we do it because the removing logic is slightly different compared to when the
headnode is not the node requiring removal). - After that we just loop over all nodes, if the next one is one that should be removed, just get it out of the list by moving the
nextpointer to thenext.nextnode. Otherwise just move along the list.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
def removeElements(self, head, val):
# empty node
if not head:
return None
# move until the first node is not val
while head is not None and head.val == val:
head = head.next
# start with non-val
current = head
while current is not None:
if current.next is not None and current.next.val == val:
# current_node.next needs removing so we simply replace it with current_node.next.next
# We know this is always "safe", because current_node.next is definitely not None (the loop condition ensures that), so we can safely access its next
current.next = current.next.next
else:
# we know that current_node.next should be kept, and so we move current_node on to be current_node.next
current = current.next
return head
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Recursion
- The idea is to change
tempwithprev,prevwithcurrent, andcurrentwithtemp.
class Solution:
def reverseList(self, head: ListNode, prev=None) -> ListNode:
if not head:
return prev
temp = head.next
head.next = prev
return self.reverseList(temp, head)
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[206/Easy] Reverse Linked List
Problem
-
Given the
headof a singly linked list, reverse the list, and return the reversed list. -
Example 1:
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]
- Example 2:
Input: head = [1,2]
Output: [2,1]
- Example 3:
Input: head = []
Output: []
- Constraints:
The number of nodes in the list is the range [0, 5000].-5000 <= Node.val <= 5000
-
Follow up: A linked list can be reversed either iteratively or recursively. Could you implement both?
- See problem on LeetCode.
Solution: Iteration
- The idea is to change
tempwithprev,prevwithcurrent, andcurrentwithtemp.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
prev = None
curr = head
while curr:
temp = curr.next
curr.next = prev
prev = curr
curr = temp
return prev
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Recursion
- The idea is to change
tempwithprev,prevwithcurrent, andcurrentwithtemp.
class Solution:
def reverseList(self, head: ListNode, prev=None) -> ListNode:
if not head:
return prev
temp = head.next
head.next = prev
return self.reverseList(temp, head)
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[214/Hard] Shortest Palindrome
Problem
-
You are given a string
s. You can convertsto a palindrome by adding characters in front of it. -
Return the shortest palindrome you can find by performing this transformation.
-
Example 1:
Input: s = "aacecaaa"
Output: "aaacecaaa"
- Example 2:
Input: s = "abcd"
Output: "dcbabcd"
- Constraints:
0 <= s.length <= 5 * 104s consists of lowercase English letters only.
- See problem on LeetCode.
Solution: Reverse string, find the suffix of the overlapping palindrome window, add it as a prefix to the original string
class Solution:
def shortestPalindrome(self, s):
# edge cases
if not s or len(s) == 1 or s == s[::-1]:
return s
# reverse string
r = s[::-1]
for i in range(len(s) + 1):
# strip characters from the end of s, i.e., s[:len(s)-i]
# strip characters from the start of r, i.e., r[:i]
# find a match which will yield the overlapping palindrome window in s and r
# (note that the r[i:] being compared is a suffix here)
# once found, add the prefix r[:i] to s
if s[:len(s)-i] == r[i:]:
# add to the start of the string
return r[:i] + s
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[228/Easy] Summary Ranges
Problem
-
You are given a sorted unique integer array
nums. -
A range
[a,b]is the set of all integers fromatob(inclusive). -
Return the smallest sorted list of ranges that cover all the numbers in the array exactly. That is, each element of
numsis covered by exactly one of the ranges, and there is no integer x such that x is in one of the ranges but not innums. -
Each range
[a,b]in the list should be output as:"a->b" if a != b"a" if a == b
-
Example 1:
Input: nums = [0,1,2,4,5,7]
Output: ["0->2","4->5","7"]
Explanation: The ranges are:
[0,2] --> "0->2"
[4,5] --> "4->5"
[7,7] --> "7"
- Example 2:
Input: nums = [0,2,3,4,6,8,9]
Output: ["0","2->4","6","8->9"]
Explanation: The ranges are:
[0,0] --> "0"
[2,4] --> "2->4"
[6,6] --> "6"
[8,9] --> "8->9"
- Constraints:
0 <= nums.length <= 20-2^31 <= nums[i] <= 2^31 - 1All the values of nums are unique.nums is sorted in ascending order.
- See problem on LeetCode.
Solution: Hold the current range in an extra variable r, format and return them
- A variation of the last solution, holding the current range in an extra variable
rto make things easier. Note thatrcontains at most two elements, so thein-check takes constant time.
class Solution:
def summaryRanges(self, nums: List[int]) -> List[str]:
ranges, r = [], []
for n in nums:
if n-1 not in r:
r = []
ranges += r,
r[1:] = n,
return ['->'.join(map(str, r)) for r in ranges] # or map('->'.join, ranges)
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: A tricky short version for Python 2
- Note that the backtick (``) operator was removed in Python 3 since it is confusingly similar to a single quote. Instead of the backtick, use the equivalent built-in function
repr().
def summaryRanges(self, nums):
ranges = r = []
for n in nums:
if `n-1` not in r:
r = []
ranges += r,
r[1:] = `n`,
return map('->'.join, ranges)
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Check if the last number and current number differ by >1; if so, add it to the output
class Solution:
def summaryRanges(self, nums: List[int]) -> List[str]:
begin, res = 0, []
strout = lambda b, e: str(b) + "->" + str(e) if b != e else str(b)
# run till "len(nums)+1" to accommodate the last number in the input
for i in range(1, len(nums)+1):
# The "i == len(nums)" check is for when we are beyond the last
# index of nums (i.e., i = len(nums)), in which case we need to
# write the output for the actual last index "nums[i-1]"
if i == len(nums) or nums[i] - nums[i-1] != 1:
res.append(strout(nums[begin], nums[i-1]))
begin = i
return res
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: Collect the ranges, then format and return them
- A variation of the first solution, without needing to hold the current range in an extra variable
r.
class Solution:
def summaryRanges(self, nums: List[int]) -> List[str]:
ranges = []
for n in nums:
if not ranges or n > ranges[-1][-1] + 1:
# add a new range list either if ranges is empty ([]) or if the current integer is greater than the previous by atleast 2
ranges += [],
# note that due to slicing below, the IndexError is avoided
# without slicing you get an IndexError: list assignment index out of range
ranges[-1][1:] = n,
# the above statement exercises two unique python features.
# to understand them, here's some examples:
# L = [1,2]
# L[2] = 3
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# IndexError: list assignment index out of range
# L[2:] = 3
#Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
#TypeError: can only assign an iterable
# L[2:] = 3, # L = [1,2,3]
# note that .join() requires an iterable with strings, so need to cast the range points to str
return ['->'.join([str(x) for x in r]) for r in ranges] # or ['->'.join(map(str, r)) for r in ranges]
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[238/Medium] Product of Array Except Self
Problem
-
Given an integer array
nums, return an array answer such thatanswer[i]is equal to the product of all the elements ofnumsexceptnums[i]. -
The product of any prefix or suffix of
numsis guaranteed to fit in a 32-bit integer. -
You must write an algorithm that runs in
O(n)time and without using the division operation. -
Example 1:
Input: nums = [1,2,3,4]
Output: [24,12,8,6]
- Example 2:
Input: nums = [-1,1,0,-3,3]
Output: [0,0,9,0,0]
- Constraints:
2 <= nums.length <= 105-30 <= nums[i] <= 30The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.
-
Follow up: Can you solve the problem in
O(1)extra space complexity? (The output array does not count as extra space for space complexity analysis.) - See problem on LeetCode.
Solution: Brute-force
def productExceptSelf(nums):
res = []
for i in range(len(nums)):
product = 1
for j in range(len(nums)):
if j == i:
continue
product *= nums[j]
res.append(product)
return res
Complexity
- Time: \(O(n^2)\)
- Space: \(O(n)\)
Solution: Two pass with division
- Note that division is not allowed per the question (this is just for reference).
def productExceptSelf1(nums):
res = []
product = 1
for i in range(len(nums)):
product *= nums[i]
for j in range(len(nums)):
res.append(int(product/nums[j]))
return res
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: Two-pass (L->R, R->L); precalculate the prefix and postfix products for each element, then multiply the corresponding prefix and postfix
- The product of elements except the
i-thone is equal to a product of elements on the left side and on the right side of that element. So the idea is to do two passes over the inputnumsand use an auxiliary listresto store intermediate results. - For the first pass, we go from left to right, i.e., from the start to the end of
nums, and on each iteration we store the accumulated product in the res at the according index such that the value of the res at thei-thindex equal to product of all elements innumsstarting from0toi-1, i.e.,res[i] = product(nums[0:i-1]). - For the second pass, we go from right to left, i.e., from the end to the start of
nums. - We accumulate a product of the prefix and postfix for each element by modifying
ressuch that the value at the indexiis equal to the product of the accumulated prefix at this index and the accumulated postfix. In the end,resis the required answer.
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
prefix = 1
res = []
# left to right
for num in nums:
res.append(prefix)
prefix *= num
# right to left
postfix = 1
for reverseIndex in range(len(nums)-1, -1,-1): # or for reverseIndex in reversed(range(len(nums))):
res[reverseIndex] *= postfix
postfix *= nums[reverseIndex]
return res
Complexity
- Time: \(O(n)\) for two passes
- Space: \(O(n)\)
[252/Easy] Meeting Rooms
Problem
-
Given an array of meeting time
intervalswhereintervals[i] = [start_i, end_i], determine if a person could attend all meetings. -
Example 1:
Input: intervals = [[0,30],[5,10],[15,20]]
Output: false
- Example 2:
Input: intervals = [[7,10],[2,4]]
Output: true
- Constraints:
0 <= intervals.length <= 104intervals[i].length == 20 <= starti < endi <= 106
- See problem on LeetCode.
Solution: Detect overlap by comparing start of current interval with end of prior interval
class Solution:
def canAttendMeetings(self, intervals: List[List[int]]) -> bool:
intervals.sort() # or the verbose: intervals.sort(key=lambda x: x[0])
for i in range(1, len(intervals)):
if intervals[i][0] < intervals[i-1][1]:
return False
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Detect overlap by comparing end of current interval with start of next interval
class Solution:
def canAttendMeetings(self, intervals: List[List[int]]) -> bool:
intervals.sort() # or the verbose: intervals.sort(key=lambda x: x[0])
for i in range(len(intervals) - 1):
if intervals[i][1] > intervals[i+1][0]:
return False
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: One-liner using all()
class Solution:
def canAttendMeetings(self, intervals: List[List[int]]) -> bool:
intervals.sort(key=lambda i: i.start)
return all(intervals[i-1].end <= intervals[i].start
for i in range(1, len(intervals)))
- Another alternative:
class Solution:
def canAttendMeetings(self, intervals: List[List[int]]) -> bool: intervals.sort(key=lambda i: i.start)
return all(i.end <= j.start for i, j in zip(intervals, intervals[1:]))
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[253/Easy] Meeting Rooms II
Problem
-
Given an array of meeting time intervals
intervalswhereintervals[i] = [start_i, end_i], return the minimum number of conference rooms required. -
Example 1:
Input: intervals = [[0,30],[5,10],[15,20]]
Output: 2
- Example 2:
Input: intervals = [[7,10],[2,4]]
Output: 1
- Constraints:
1 <= intervals.length <= 1040 <= starti < endi <= 106
- See problem on LeetCode.
Solution: Min-heap to store the earliest ending time
- The bottom-line is that we need to know when we need a new room and when we can share the room.
- We sort the interval time slot by the start time.
- The definition of overlap: the end time of the current time slot is larger than the begin time of the next time slot, for e.g.,
[1,11],[10,19], since11 > 10, there is an overlap. - If there is an overlap between the current time slot and the smallest end time in the minimum heap, we need a new room for the meeting.
- If there is no overlap between the current time and the smallest end time in the minimum heap, we don’t need a new room for the meeting since we can use the the same room of the smallest end time. But we still need the end time in the future to help us decide whether we have an overlap or not.
- We use a minimum heap to store the \(k\)-largest end time we meet until now.
- If the current time slot’s begin time is larger than the smallest end time in the minimum heap, i.e., we don’t have overlap, which implies we don’t need a new room, which in turn means that we can share the room with the smallest end time in the minimum heap. However, we need to update the minimum heap by using the
replacemethod. - If the current time slot’s begin time is less than the smallest end time in the minimum heap, we have an overlap now, i.e., we need a new room, we to use the
heappushmethod to push the current time slot’s end time into the minimum heap.
- If the current time slot’s begin time is larger than the smallest end time in the minimum heap, i.e., we don’t have overlap, which implies we don’t need a new room, which in turn means that we can share the room with the smallest end time in the minimum heap. However, we need to update the minimum heap by using the
- Note that
heapq.heapreplace(heap, item)pops and returns the smallest item from the heap, and also push the new item. The heap size doesn’t change.
import heapq
class Solution:
def minMeetingRooms(self, intervals: List[List[int]]) -> int:
intervals = sorted(intervals, key=lambda x: x[0]) # Sort by start value
heap = []
for i in intervals:
if heap and heap[0] <= i[0]:
# If the new start time is greater than or equal to the exist end time, means the room has been released, replace the previous time with the new ending time
# replacing because start time >= end time of heap[0], we can reuse the same meeting room that we used before
heapq.heapreplace(heap, i[-1])
else:
# The room is still in use, add (push a new end time to min heap) a new room
heapq.heappush(heap, i[-1])
return len(heap)
Complexity
- Time: $$O(n\log{n})
- Space: \(O(1)\)
Solution: Greedy Interval Partition
- This is an interval partition problem based on two heuristics:
- We process intervals ordered by starting time and assign each interval to a ‘current vacant’ room.
- We only check the room with the earliest ending time for global vacancy. If there is no vacant room, we add one.
- Since we iterate intervals by starting time, there is no better choice than current interval as rest intervals would all request one more room if current one does. And we also need to track the ending time since we need to determine whether there exists a vacant room at specific time. We only track the earliest ending time as we only check this room for vacancy. If this room is not vacant, there is no need to check the rest and we just add one more room.
- So combining both heuristics, we can sort starting time and ending time separately. We iterate starting time and use a pointer to track current the earliest ending time. So
sis current interval’s starting time andearliestEndingTimeIdxis the pointer to current earliest ending time. Ifs < ends[earliestEndingTimeIdx], there is no vacant room, we add one more room. Otherwise, we assign current interval to a vacant room and our current earliest ending time should be updated toends[earliestEndingTimeIdx+1].
class Solution:
def minMeetingRooms(self, intervals: List[List[int]]) -> int:
starts = sorted(i[0] for i in intervals)
ends = sorted(i[1] for i in intervals)
earliestEndingTimeIdx = roomCount = 0
for s in starts:
if s < ends[earliestEndingTimeIdx]:
# current earliest ending time room unavailable, add a vacant room
roomCount += 1
else:
# earliest ending room was available and taken; look for the next earliest one
earliestEndingTimeIdx += 1
return roomCount
Complexity
- Time: \(O(n\log{n} + n\log{n} + n) = O(n\log{n})\) since sorting takes \(O(n\log{n})\) and one greedy pass takes \(O(n)\)
- Space: \(O(1)\)
[270/Easy] Closest Binary Search Tree Value
Problem
-
Given the
rootof a binary search tree and atargetvalue, return the value in the BST that is closest to thetarget. -
Example 1:
Input: root = [4,2,5,1,3], target = 3.714286
Output: 4
- Example 2:
Input: root = [1], target = 4.428571
Output: 1
- Constraints:
The number of nodes in the tree is in the range [1, 104].0 <= Node.val <= 109-109 <= target <= 109
- See problem on LeetCode.
Solution: Recursion
- Closest is either the root’s value (
a) or the closest in the appropriate subtree (b).
class Solution(object):
def closestValue(self, root, target):
a = root.val
kid = root.left if target < a else root.right
if not kid: return a
b = self.closestValue(kid, target)
return min((b, a), key=lambda x: abs(target - x))
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: Iteration
- Walk the path down the tree close to the target, return the closest value on the path.
class Solution(object):
def closestValue(self, root, target):
path = []
while root:
path += root.val,
root = root.left if target < root.val else root.right
return min(path[::-1], key=lambda x: abs(target - x))
- Note that the
[::-1]is only for handling targets much larger than 32-bit integer range, where different path values x have the same “distance”, i.e.,abs(x - target). In such cases, the leaf value is the correct answer. If such large targets aren’t asked, then it’s unnecessary.
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: Iteration with \(O(1)\) space
- In the code below,
root.valis the present root we are currently at during each traversal from the root to the left subtree and/or right subtree; while ourclosestis what we are using to track the minimumroot.valwe have seen so far, we are updating ourclosestanytime we come across(root.val - target) < previous closest.
class Solution(object):
def closestValue(self, root, target):
closest = root.val
while root:
if abs(root.val - target) < abs(closest - target):
closest = root.val
root = root.left if target < root.val else root.right
return closest
- Same approach; rehashed:
class Solution(object):
def closestValue(self, root, target):
closest = root.val
while root:
closest = min((root.val, closest), key=lambda x: abs(target - x))
root = root.left if target < root.val else root.right
return closest
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[277/Medium] Find the Celebrity
Problem
-
Suppose you are at a party with
npeople labeled from0ton - 1and among them, there may exist one celebrity. The definition of a celebrity is that all the othern - 1people know the celebrity, but the celebrity does not know any of them. -
Now you want to find out who the celebrity is or verify that there is not one. The only thing you are allowed to do is ask questions like: “Hi, A. Do you know B?” to get information about whether A knows B. You need to find out the celebrity (or verify there is not one) by asking as few questions as possible (in the asymptotic sense).
-
You are given a helper function
bool knows(a, b)that tells you whether A knows B. Implement a functionint findCelebrity(n). There will be exactly one celebrity if they are at the party. -
Return the celebrity’s label if there is a celebrity at the party. If there is no celebrity, return
-1. -
Example 1:
Input: graph = [[1,1,0],[0,1,0],[1,1,1]]
Output: 1
Explanation: There are three persons labeled with 0, 1 and 2. graph[i][j] = 1 means person i knows person j, otherwise graph[i][j] = 0 means person i does not know person j. The celebrity is the person labeled as 1 because both 0 and 2 know him but 1 does not know anybody.
- Example 2:
Input: graph = [[1,0,1],[1,1,0],[0,1,1]]
Output: -1
Explanation: There is no celebrity.
- Constraints:
n == graph.lengthn == graph[i].length2 <= n <= 100graph[i][j] is 0 or 1.graph[i][i] == 1
-
Follow up: If the maximum number of allowed calls to the API
knowsis3 * n, could you find a solution without exceeding the maximum number of calls? - See problem on LeetCode.
Solution: Three loops; find a candidate, check if they everyone before them, and if everyone knows them
- Explanation:
- The first loop is to exclude
n - 1labels that are not possible to be a celebrity. - After the first loop,
xis the only candidate. - The second and third
any()statements are to verifyxis actually a celebrity by definition. - The key part is the first loop. To understand this you can think the
knows(a,b)as aa < bcomparison, ifaknowsbthena < b, ifadoes not knowb,a > b. Then if there is a celebrity, he/she must be the - “maximum” of thenpeople. - However, the “maximum” may not be the celebrity in the case of no celebrity at all. Thus we need the second and third
any()statements to check ifxis actually celebrity by definition. - The total calls of knows is thus
3nat most. One small improvement is that in the second loop we only need to checkiin the range[0, x). You can figure that out yourself easily.
- The first loop is to exclude
# The knows API is already defined for you.
# return a bool, whether a knows b
# def knows(a: int, b: int) -> bool:
class Solution:
def findCelebrity(self, n: int) -> int:
# Iterate through each person and find a candidate to be the celebrity
# The resulting candidate must be a celebrity by the following logic
# If there is a celebrity, they must
# a) be known by every person before them (thus, end up as "cand" at some point)
# b) not know anyone after them (thus, never relinquish "cand")
cand = 0
for i in range(n):
if knows(cand, i):
cand = i
# We've established that cand does not know anyone after it
# Let's establish that cand does not know everyone before it
if any(knows(cand, i) for i in range(cand)):
return -1
# Last thing we don't know:
# Does everyone know cand?
if any(not knows(i, cand) for i in range(n)):
return -1
return cand
- Same solution; expanded a bit by converting the
any()calls toforloops:
class Solution(object):
def findCelebrity(self, n):
"""
:type n: int
:rtype: int
"""
# Iterate through each person and find a candidate to be the celebrity
# The resulting candidate must be a celebrity by the following logic
# If there is a celebrity, they must
# a) be known by every person before them (thus, end up as "cand" at some point)
# b) not know anyone after them (thus, never relinquish "cand")
cand = 0
for i in range(n):
if knows(cand, i):
cand = i
# We've established that cand does not know anyone after it
# Let's establish that cand is known by, but does not know everyone before it
for i in range (0, cand):
if knows(cand, i):
return -1
if not knows(i, cand):
return -1
# Last thing we don't know:
# Does everyone after cand know cand?
for i in range(cand, n):
if not knows(i, cand):
return -1
return cand
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Two loops
class Solution:
def findCelebrity(self, n: int) -> int:
# Iterate through each person and find a candidate to be the celebrity
# The resulting candidate must be a celebrity by the following logic
# If there is a celebrity, they must
# a) be known by every person before them (thus, end up as "cand" at some point)
# b) not know anyone after them (thus, never relinquish "cand")
celebrity = 0
for i in range(1,n):
if knows(celebrity,i):
celebrity = i
# We've established that cand does not know anyone after it
# Let's establish that cand is known by everyone but cand does not know anyone
if celebrity != i and (knows(celebrity,i) or not knows(i, celebrity)):
return -1
return celebrity
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[283/Easy] Move Zeroes
Problem
-
Given an integer array
nums, move all 0’s to the end of it while maintaining the relative order of the non-zero elements. -
Note that you must do this in-place without making a copy of the array.
-
Example 1:
Input: nums = [0,1,0,3,12]
Output: [1,3,12,0,0]
- Example 2:
Input: nums = [0]
Output: [0]
- Constraints:
1 <= nums.length <= 104-2^31 <= nums[i] <= 2^31 - 1
- See problem on LeetCode.
Solution: Keep track of position of the first zero and the first non-zero value after the first zero, swap them
- Algorithm:
- We use
zeroto keep track of position of the first zero in the list (which changes as we go) andito keep track of the first non-zero value after the first zero. - Each time we have
zeropoint to a zero andipoint to the first non-zero afterzero, we swap the values that store atiandzero. - By doing this, we move zeros towards the end of the list gradually until
ireaches the end. - And when it does, we are done.
- We use
- Remarks:
- No return value needed, since we are doing in-place modification.
- We use
nums[i],nums[j] = nums[j],nums[i]to achieve the in-place modification because Python allows you to swaps values in a list using syntax:x, y = y, x.
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
zero = 0 # records the position of "0"
for i in range(len(nums)):
if nums[i] != 0:
nums[i], nums[zero] = nums[zero], nums[i]
zero += 1
- Note that this solution is inefficient when all nums are non zeroes since you are still swapping the variable with itself. To avoid this, check if
iandzeroare different pointers before swapping:
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
zero = 0 # records the position of "0"
for i in range(len(nums)):
if nums[i] != 0:
if i != zero:
nums[i], nums[zero] = nums[zero], nums[i]
zero += 1
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: del a zero and append one
class Solution(object):
def moveZeroes(self, nums: List[int]) -> None:
i = 0
end = len(nums)
while i < end:
if nums[i] == 0:
del nums[i]
nums.append(0)
end -= 1
else:
i += 1
- Same approach; rehashed:
class Solution(object):
def moveZeroes(self, nums: List[int]) -> None:
"""
:type nums: List[int]
:rtype: void Do not return anything, modify nums in-place instead.
"""
for _ in range(nums.count(0)):
nums.remove(0)
nums.append(0)
Complexity
- Time: \(O(n^2)\) since the
deloperation takes \(O(n)\) time - Space: \(O(1)\)
[289/Medium] Game of Life
Problem
-
According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.”
-
The board is made up of an
m x ngrid of cells, where each cell has an initial state: live (represented by a1) or dead (represented by a0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):- Any live cell with fewer than two live neighbors dies as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by over-population.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
-
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the
m x ngridboard, return the next state. -
Example 1:
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
- Example 2:
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]
- Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 25board[i][j] is 0 or 1.
- Follow up:
- Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
- In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?
- See problem on LeetCode.
Solution: In-place board modify
- In-place manipulation. At first glance, I thought it was to be solved by DFS/BFS. However, the key word is:
simultaneously, so no DFS/BFS. - When the value needs to be updated, we do not just change
0 to 1/1 to 0but we do in increments and decrements of2. Check the table below:
previous value state change current state current value
0 no change dead 0
1 no change live 1
0 changed (+2) live 2
1 changed (-2) dead -1
- In other words:
apply by using:
under-population: < 2
live to next generation: 2 or 3
over-population: > 3
reproduction: == 3
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
directions = set((x,y) for x in (-1, 0, 1) for y in (-1, 0, 1) if x or y)
# or directions = [(1,0), (1,-1), (0,-1), (-1,-1), (-1,0), (-1,1), (0,1), (1,1)]
# all new 0's denoted as -1 (1 ==> 0)
# all new 1's denoted as 2 (0 ==> 1)
for i in range(len(board)):
for j in range(len(board[0])):
# Live neighbors count
live = 0
# Check and count neighbors in all directions
for x, y in directions:
if (i + x < len(board) and i + x >= 0) and (j + y < len(board[0]) and j + y >=0) and abs(board[i + x][j + y]) == 1: # originally 1's
live += 1
# Rule 1 or Rule 3
if board[i][j] == 1 and (live < 2 or live > 3):
board[i][j] = -1
# Rule 4
if board[i][j] == 0 and live == 3:
board[i][j] = 2
for i in range(len(board)):
for j in range(len(board[0])):
board[i][j] = 1 if(board[i][j] > 0) else 0
return board
Complexity
- Time: \(O(m \times n)\) where the board is made up of an
m x ngrid of cells - Space: \(O(1)\)
[Easy] Moving Average with Cold Start
Problem
-
Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
-
Example:
Input:
a = [1, 10, 3, 5]
windowSize = 3
Output:
1.0
5.5
4.66667
6.0
Solution: Deque
from collections import deque
queue = deque()
windowSize = 3
for i in range(len(a)):
if windowSize > len(queue):
queue.append(a[i])
print(sum(queue)/len(queue))
else:
queue.popleft()
queue.append(a[i])
print(sum(queue)/windowSize)
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[346/Easy] Moving Average from Data Stream
Problem
-
Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
-
Implement the
MovingAverageclass:MovingAverage(int size)Initializes the object with the size of the window size.double next(int val)Returns the moving average of the lastsizevalues of the stream.
-
Example 1:
Input
["MovingAverage", "next", "next", "next", "next"]
[[3], [1], [10], [3], [5]]
Output
[null, 1.0, 5.5, 4.66667, 6.0]
Explanation
MovingAverage movingAverage = new MovingAverage(3);
movingAverage.next(1); // return 1.0 = 1 / 1
movingAverage.next(10); // return 5.5 = (1 + 10) / 2
movingAverage.next(3); // return 4.66667 = (1 + 10 + 3) / 3
movingAverage.next(5); // return 6.0 = (10 + 3 + 5) / 3
- Constraints:
1 <= size <= 1000-105 <= val <= 105At most 104 calls will be made to next.
- See problem on LeetCode.
Solution: Deque
import collections
class MovingAverage(object):
def __init__(self, size: int):
"""
Initialize your data structure here.
:type size: int
"""
self.queue = collections.deque(maxlen=size)
def next(self, val: int) -> float:
"""
:type val: int
:rtype: float
"""
queue = self.queue
# Appending to a `maxlen` deque will
# automatically popleft the leftmost element
queue.append(val)
return float(sum(queue))/len(queue)
# Your MovingAverage object will be instantiated and called as such:
# obj = MovingAverage(size)
# param_1 = obj.next(val)
- Same approach; more explicit deque sizing (with
self.maxandself.currLength):
from collections import deque
class MovingAverage:
def __init__(self, size: int):
"""
Initialize your data structure here.
"""
self.currLength = 0
self.max = size
self.sum = 0
self.queue = deque()
def next(self, val: int) -> float:
if self.currLength < self.max:
self.currLength +=1
else:
self.sum -= self.queue.popleft()
self.queue.append(val)
self.sum += val
return self.sum/self.currLength
- Even more cleaner:
from collections import deque
class MovingAverage:
def __init__(self, size: int):
"""
Initialize your data structure here.
"""
self.size = size
self.queue = deque()
self.sum = 0
def next(self, val: int) -> float:
if len(self.queue) >= self.size:
# Remove leftmost element value
# from sum and from the deque
self.sum -= self.queue.popleft()
self.queue.append(val)
self.sum += val
return self.sum/len(self.queue)
Complexity
- Time: \(O(1)\) since queue takes \(O(1)\) to insert.
- Space: \(O(n)\) where \(n\) is the size of queue. The algorithm needs to maintain two integers:
sumandnumVal, and a queue. So it uses linear space.
[383/Easy] Ransom Note
Problem
-
Given two strings
ransomNoteandmagazine, return true ifransomNotecan be constructed frommagazineand false otherwise. -
Each letter in
magazinecan only be used once inransomNote. -
Example 1:
Input: ransomNote = "a", magazine = "b"
Output: false
- Example 2:
Input: ransomNote = "aa", magazine = "ab"
Output: false
- Example 3:
Input: ransomNote = "aa", magazine = "aab"
Output: true
- Constraints:
1 <= ransomNote.length, magazine.length <= 105ransomNote and magazine consist of lowercase English letters.
- See problem on LeetCode.
Solution: For each unique char in ransomNote, check if it’s count in ransomNote doesn’t exceed that in magazine
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
for i in set(ransomNote):
if ransomNote.count(i) > magazine.count(i):
return False
return True
Solution: Remove ransomNote chars from magazine; confirm if length of ransomNote = 0
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
for i in ransomNote:
if i not in magazine:
return False
# str.replace(old, new[, count]) returns a copy of the string with all occurrences
# of the substring old replaced by new.
# If the optional argument count is given, only the first count occurrences are replaced.
# https://docs.python.org/3/library/stdtypes.html#str.replace
magazine = magazine.replace(i, "", 1)
if not len(ransomNote):
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[384/Medium] Shuffle an Array
Problem
-
Given an integer array
nums, design an algorithm to randomly shuffle the array. All permutations of the array should be equally likely as a result of the shuffling. - Implement the
Solutionclass:Solution(int[] nums)Initializes the object with the integer array nums.int[] reset()Resets the array to its original configuration and returns it.int[] shuffle()Returns a random shuffling of the array.
- Example 1:
Input
["Solution", "shuffle", "reset", "shuffle"]
[[[1, 2, 3]], [], [], []]
Output
[null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]
Explanation
Solution solution = new Solution([1, 2, 3]);
solution.shuffle(); // Shuffle the array [1,2,3] and return its result.
// Any permutation of [1,2,3] must be equally likely to be returned.
// Example: return [3, 1, 2]
solution.reset(); // Resets the array back to its original configuration [1,2,3]. Return [1, 2, 3]
solution.shuffle(); // Returns the random shuffling of array [1,2,3]. Example: return [1, 3, 2]
-
Constraints:
1 <= nums.length <= 50-106 <= nums[i] <= 106All the elements of nums are unique.At most 104 calls in total will be made to reset and shuffle.
-
See problem on LeetCode.
Solution
class Solution:
def __init__(self, nums: List[int]):
self.nums = nums
# keep a backup copy
self.arr = nums[:]
def reset(self) -> List[int]:
# make sure to not directly assign self.arr to self.nums
# since that will mean we will lose our backup once
# we start modifying it
self.nums = self.arr[:]
return self.nums
def shuffle(self) -> List[int]:
# shuffle returns none, so copy and shuffle
# approach 1
# random.shuffle(self.nums)
# return self.nums
# approach 2
for i in range(len(self.nums)):
# Fisher-Yates Algorithm
# generate an index in [i, len(ans))
# note that random.range(a, b) returns a random number between [a, b)
# while random.randint(a, b) returns a random number between [a, b]
# i.e., including both end points.
num = random.randrange(i, len(self.nums))
# swap ans[num] and ans[i]
self.nums[i], self.nums[num] = self.nums[num], self.nums[i]
return self.nums
# Your Solution object will be instantiated and called as such:
# obj = Solution(nums)
# param_1 = obj.reset()
# param_2 = obj.shuffle()
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for
self.numsand theself.arrbackup
[398/Medium] Random Pick Index
Problem
-
Given an integer array
numswith possible duplicates, randomly output the index of a giventargetnumber. You can assume that the given target number must exist in the array. - Implement the
Solutionclass:Solution(int[] nums): Initializes the object with the array nums.int pick(int target): Picks a random indexifromnumswherenums[i] == target. If there are multiple validi’s, then each index should have an equal probability of returning.
- Example 1:
Input
["Solution", "pick", "pick", "pick"]
[[[1, 2, 3, 3, 3]], [3], [1], [3]]
Output
[null, 4, 0, 2]
Explanation
Solution solution = new Solution([1, 2, 3, 3, 3]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums[0] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
- Constraints:
1 <= nums.length <= 2 * 104-2^31 <= nums[i] <= 2^31 - 1target is an integer from nums.At most 104 calls will be made to pick.
- See problem on LeetCode.
Solution: Form index of targets in pick and use random.choice() to pick elements from a uniform distribution
import random
class Solution:
def __init__(self, nums: List[int]):
self.nums = nums
def pick(self, target: int) -> int:
# answer is a list of indices containing the target
answer = []
for idx, num in enumerate(self.nums):
if target == num:
answer.append(idx)
# random.choice() samples uniformly (with PDF = 1/(b-a) where [a,b] are the min and max elements in the data distribution)
return random.choice(answer)
# Your Solution object will be instantiated and called as such:
# obj = Solution(nums)
# param_1 = obj.pick(target)
Complexity
- Time: \(O(n)\) for
pick() - Space: \(O(n)\) for
answer
Solution: Compute index of targets in __init__ using and use random.choice() to pick elements from a uniform distribution
import random
class Solution:
def __init__(self, nums: List[int]):
self.hash = defaultdict(list)
for i, num in enumerate(nums):
self.hash[num].append(i)
def pick(self, target: int) -> int:
return random.choice(self.hash[target])
Complexity
- Time: \(O(1)\) for
pick() - Space: \(O(n)\) for
hash
[409/Easy] Longest Palindrome
Problem
- Given a string
swhich consists of lowercase or uppercase letters, return the length of the longest palindrome that can be built with those letters. -
Letters are case sensitive, for example,
"Aa"is not considered a palindrome here. - Example 1:
Input: s = "abccccdd"
Output: 7
Explanation:
One longest palindrome that can be built is "dccaccd", whose length is 7.
- Example 2:
Input: s = "a"
Output: 1
- Example 3:
Input: s = "bb"
Output: 2
- Constraints:
1 <= s.length <= 2000s consists of lowercase and/or uppercase English letters only.
- See problem on LeetCode.
Solution: Add the number of even characters to the result; if an odd character is found, add only one of it to the result for a string to be palindrome
- For a string to be palindrome, it needs characters that occur an even number of times. For e.g.,
aabbaaoraaa. - If a character occurs once, i.e., an odd number of times, we can accommodate only one such character. For e.g.,
abaoraacbcaa. In other words, a second character occurring once will need to be discarded for the string to still be a palindrome.
class Solution:
def longestPalindrome(self, s: str) -> int:
counts = Counter(s)
res = 0
foundOdd = False
for val in counts.values():
if not val%2:
res += val
else:
foundOdd = True
# add even occurrences of the char to res by subtracting 1 from its count
res += val-1
# add only one instance of the odd character to res
return res+1 if foundOdd else res
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for
counts
[415/Easy] Add Strings
Problem
- Given two non-negative integers,
num1andnum2represented as string, return the sum ofnum1andnum2as a string. - You must solve the problem without using any built-in library for handling large integers (such as
BigInteger). You must also not convert the inputs to integers directly. - Example 1:
Input: num1 = "11", num2 = "123"
Output: "134"
- Example 2:
Input: num1 = "456", num2 = "77"
Output: "533"
- Example 3:
Input: num1 = "0", num2 = "0"
Output: "0"
- Constraints:
1 <= num1.length, num2.length <= 104num1 and num2 consist of only digits.num1 and num2 don't have any leading zeros except for the zero itself.
- See problem on LeetCode.
Solution: Use a Dictionary
class Solution:
def addStrings(self, num1: str, num2: str) -> str:
def str2int(num):
numDict = {'0' : 0, '1' : 1, '2' : 2, '3' : 3, '4' : 4, '5' : 5,
'6' : 6, '7' : 7, '8' : 8, '9' : 9}
output = 0
for d in num:
output = output * 10 + numDict[d]
return output
return str(str2int(num1) + str2int(num2))
Complexity
- Time: \(O(n + n) = O(2n) = O(n)\)
- Space: \(O(1)\)
Solution: Use ord to get unicode
class Solution:
def addStrings(self, num1: str, num2: str) -> str:
def str2int(num):
result = 0
for n in num:
result = result * 10 + ord(n) - ord('0')
return result
return str(str2int(num1) + str2int(num2))
Complexity
- Time: \(O(n + n) = O(2n) = O(n)\)
- Space: \(O(1)\)
[435/Medium] Non-overlapping Intervals
Problem
-
Given an array of intervals
intervalswhereintervals[i] = [start_i, end_i], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping. -
Example 1:
Input: intervals = [[1,2],[2,3],[3,4],[1,3]]
Output: 1
Explanation: [1,3] can be removed and the rest of the intervals are non-overlapping.
- Example 2:
Input: intervals = [[1,2],[1,2],[1,2]]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of the intervals non-overlapping.
- Example 3:
Input: intervals = [[1,2],[2,3]]
Output: 0
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.
- Constraints:
1 <= intervals.length <= 105intervals[i].length == 2-5 * 104 <= starti < endi <= 5 * 104
- See problem on LeetCode.
Solution: Sort by start time
- Algorithm:
- Attend the one with smaller start time first
- (Greedy) Remove the one with bigger end time if an overlap occurs (because it will always incur more overlappings in the remaining array with ascending order of start time)
- Example:
[[1,10], [2,3], [3,4], [5,6]]
First, we attend [1,10]
Next, [2,3] overlaps with [1,10] as 2 < 10 (i.e., [2,3] starts before [1,10] ends). Here, we are going to remove [1,10] as it would definitely produce more overlappings as we continue the iteration.
Thirdly, attend [3,4]
Last, attend [5,6]
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
intervals.sort()
prev = float("-inf")
remove = 0
for i in intervals:
if i[0] >= prev:
# no overlap case: the current interval starts after prev ended
# thus, no need to remove, just update prev
prev = i[1]
else:
# overlap case: the current interval starts before prev ended
# remove the interval with the larger end time
# and update prev to hold the smaller end time
remove += 1
prev = min(prev, i[1])
return remove
Complexity
- Time: \(O(n\log{n})\) due to sorting
- Space: \(O(1)\)
Solution: Sort by end time
-
If we think more clearly, the first solution can be improved slightly (save a line of code) by sorting the intervals with end time. Why? Because the greedy nature remains true even if we the remaining array is not sorted by start time. Meanwhile, if we sort them by end time and if overlap occurs, the interval that comes later must be the one to remove as it has larger end time. Take a look at the following example.
-
Example:
1) sort by start time
Extra procedure: after comparing [1,10] and [2,3], we have to choose which one to remove by comparing the end time.
[[1,10], [2,3], [3,4], [5,6]]
2) sort by end time
Saved procedure: after comparing [5, 6] and [1,10], we immediately can remove the later one which is [1,10] as it must produce more overlaps in the following, i.e. with [6,11] and [9,12].
[[2,3], [3,4], [5,6], [1,10], [6, 11], [9, 12]]
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
intervals.sort(key=lambda x: x[1]) # sort based on end times
prev = float("-inf")
remove = 0
for i in intervals:
if i[0] >= prev:
# no overlap case: the current interval starts after prev ended
# thus, no need to remove, just update prev
prev = i[1]
else:
# overlap case: the current interval starts before prev ended
remove += 1
return remove
Complexity
- Time: \(O(n\log{n})\) due to sorting
- Space: \(O(1)\)
[442/Medium] Find All Duplicates in an Array
Problem
-
Given an integer array
numsof lengthnwhere all the integers ofnumsare in the range[1, n]and each integer appears once or twice, return an array of all the integers that appears twice. -
You must write an algorithm that runs in
O(n)time and uses only constant extra space. -
Example 1:
Input: nums = [4,3,2,7,8,2,3,1]
Output: [2,3]
- Example 2:
Input: nums = [1,1,2]
Output: [1]
- Example 3:
Input: nums = [1]
Output: []
- Constraints:
n == nums.length1 <= n <= 1051 <= nums[i] <= nEach element in nums appears once or twice.
- See problem on LeetCode.
Solution: Use the given array as a hashmap, add element to itself, divide by two to get duplicates
class Solution:
def findDuplicates(self, nums: List[int]) -> List[int]:
"""
We can't use an extra hashmap because space complexity has to be O(1).
So let's use the given array as hashmap based on the logic that the all numbers are in the range of 1-n so we can use the index of array as the numbers (index+1 as 0th index will represent 1) keys of hashmap and the values as the number of occurrences of each number.
We can achieve the above be decrementing each element by 1 to sustain the nth index as max value of array will be n but max index would be n-1.
Now we will iterate over the array and will treat each element as the correct index of number.
Everytime we encounter a number, the value at its correct index will be incremented by n.
At the end we divide each number by n so that we get the count of each number(index of array) as the values of array.
Now the elements with value == 2 would be the duplicates.
"""
n = len(nums)
nums = [num-1 for num in nums]
print(nums)
for num in nums:
nums[num % n] += n
output = []
for key, num in enumerate(nums):
if num//n == 2:
output.append(key+1)
# or output = [(key+1) for key, num in enumerate(nums) if num//n == 2]
return output
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Cyclic Sort
class Solution:
def cyclicSort(self, nums):
i = 0
while i < len(nums):
correct = nums[i] - 1
if nums[correct] != nums[i]:
nums[correct], nums[i] = nums[i], nums[correct]
else:
i += 1
def findDuplicates(self, nums: List[int]) -> List[int]:
self.cyclicSort(nums)
output = []
for i in range(len(nums)):
if nums[i] != i+1:
output.append(nums[i])
return output
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Marking using the given array as a hashmap
class Solution:
def findDuplicates(self, nums: List[int]) -> List[int]:
output = []
"""
Since we have to solve this problem in constant space complexity so the only way is to use the space of given array and manipulate it.
Since the elements in the array are in range [1..n], we can consider the elements as idexes also and to be precise (element - 1) as it is a 0-indexed array.
Since we can't use any extra space so let us mark the elements encountered in the given array only. This can be done by multiplying the element with -1.
Now for each element, we will treat it as the index and check whether the value present at that index is visited or not. If it is visited then it is a duplicate else we mark that element as visited(multiply by -1).
"""
for num in nums:
if nums[abs(num) - 1] < 0:
output.append(abs(num))
else:
nums[abs(num) - 1] *= -1
return output
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[443/Medium] String Compression
Problem
-
Given an array of characters
chars, compress it using the following algorithm: -
Begin with an empty string
s. For each group of consecutive repeating characters inchars:- If the group’s length is
1, append the character tos. - Otherwise, append the character followed by the group’s length.
- If the group’s length is
-
The compressed string
sshould not be returned separately, but instead, be stored in the input character arraychars. Note that group lengths that are10or longer will be split into multiple characters in chars. -
After you are done modifying the input array, return the new length of the array.
-
You must write an algorithm that uses only constant extra space.
-
Example 1:
Input: chars = ["a","a","b","b","c","c","c"]
Output: Return 6, and the first 6 characters of the input array should be: ["a","2","b","2","c","3"]
Explanation: The groups are "aa", "bb", and "ccc". This compresses to "a2b2c3".
- Example 2:
Input: chars = ["a"]
Output: Return 1, and the first character of the input array should be: ["a"]
Explanation: The only group is "a", which remains uncompressed since it's a single character.
- Example 3:
Input: chars = ["a","b","b","b","b","b","b","b","b","b","b","b","b"]
Output: Return 4, and the first 4 characters of the input array should be: ["a","b","1","2"].
Explanation: The groups are "a" and "bbbbbbbbbbbb". This compresses to "ab12".
- Constraints:
1 <= chars.length <= 2000chars[i] is a lowercase English letter, uppercase English letter, digit, or symbol.
- See problem on LeetCode.
Solution: Slow/fast pointers
- Slow:
currentIdx(the idx ready to be modified) - Fast:
i(traversing the string to find how many times a char is repeated before moving onto the next char)
class Solution:
def compress(self, chars):
"""
:type chars: List[str]
:rtype: int
"""
# count: record the times one element had appeared.
count = 1
# currentIdx: the idx ready to be modified.
currentIdx = 0
for i in range(1, len(chars)+1):
# check for valid index and if current char matches the previous char
# if so, add to count
if i < len(chars) and chars[i] == chars[i-1]:
count += 1
# Look for a new element
else:
# 1) update letter: we modify char[currentIdx] to the char we're writing the count for.
chars[currentIdx] = chars[i-1]
currentIdx += 1
# 2) append count to string after char
if count == 1:
# if the previous element only appear once, skip below.
continue
# add count digit by digit
for ch in str(count):
chars[currentIdx] = ch
currentIdx += 1
# 3) reset count because we're done with the current element
count = 1
return currentIdx
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) because the input is modified in-place
[523/Medium] Continuous Subarray Sum
Problem
-
Given an integer array
numsand an integerk, returntrueifnumshas a continuous subarray of size at least two whose elements sum up to a multiple ofk, or false otherwise. -
An integer
xis a multiple ofkif there exists an integernsuch thatx = n * k. 0 is always a multiple of k. -
Example 1:
Input: nums = [23,2,4,6,7], k = 6
Output: true
Explanation: [2, 4] is a continuous subarray of size 2 whose elements sum up to 6.
- Example 2:
Input: nums = [23,2,6,4,7], k = 6
Output: true
Explanation: [23, 2, 6, 4, 7] is an continuous subarray of size 5 whose elements sum up to 42.
42 is a multiple of 6 because 42 = 7 * 6 and 7 is an integer.
- Example 3:
Input: nums = [23,2,6,4,7], k = 13
Output: false
- Constraints:
1 <= nums.length <= 1050 <= nums[i] <= 1090 <= sum(nums[i]) <= 2^31 - 11 <= k <= 2^31 - 1
- See problem on LeetCode.
Solution
- Same as subarray
sumequalskwith modification. Basic idea is that, if you get the same remainder again, it means that you’ve encountered some sum which is a multiple ofk.
class Solution:
def checkSubarraySum(self, nums: List[int], k: int) -> bool:
d = {0: -1}
prefix_sum = 0
for i, num in enumerate(nums):
prefix_sum += num
if k != 0:
prefix_sum = prefix_sum % k
if prefix_sum in d:
# we know that sum between mp[prefix_sum] + 1 and i is multiple of k, so I don't have to include mp[prefix_sum]
if i - d[prefix_sum] > 1:
return True
else:
# if prefix_sum doesn't exists, then add its index, otherwise don't update it, it is preferable to keep the
# oldest index, so that you can get length of atleast 2.
d[prefix_sum] = i
return False
- Explanation with example:
Example:
nums = [23,2,4], k = 6
Lets walk through the code with the example.
(i=0) : prefix_sum = 23 => 23%6 => (prefix_sum = 5)
(i=1) : prefix_sum = 5+2=7 => 7%6 => (prefix_sum = 1)
(i=2) : prefix_sum = 1+4=5 => 5%6 => (prefix_sum = 5)
- We have encountered the same
prefix_sum(remainder)again which means we have the subarray ofprefix_sum%k = 0. - But, there’s another aspect to this problem. The subarray must have a minimum size of 2.
- That is why we check if
(i - d[prefix_sum]) > 1. - In the above example, this if loop is executed when (
i=2) and (mp[prefix_sum]=1). - In other words, the same remainder (
prefix_sum=5) has been encountered twice and then we check for the respective difference in indices.
Counter example to understand this. Lets take nums = [23,6], k = 6
(i=0) : prefix_sum = 23 => 23%6 => (prefix_sum = 5)
(i=1) : prefix_sum = 5+6=11 => 11%6 => (prefix_sum = 5)
- So, the same
prefix_sum(remainder) has appeared again which means we’ve found the subarray but it is not a subarray of size 2 or more. - Because they’ve occurred next to each other, which means that, we have just one element in the subarray which contributes.
- If you remove
23from thenumsarray and keep6alone, it will still be a subarray whoseprefix_sum%kis 0. But, we want a subarray of size 2 or more. - This is the reason why we calculate the index difference and then return
True. - Also, if
k==0, you don’t need to find the remainder. So, you just keep addingprefix_sumand repeat the rest of the process.
[556/Medium] Next Greater Element III
Problem
-
Given a positive integer
n, find the smallest integer which has exactly the same digits existing in the integernand is greater in value thann. If no such positive integer exists, return-1. -
Note that the returned integer should fit in 32-bit integer, if there is a valid answer but it does not fit in 32-bit integer, return
-1. -
Example 1:
Input: n = 12
Output: 21
- Example 2:
Input: n = 21
Output: -1
- Constraints:
1 <= n <= 231 - 1
- See problem on LeetCode.
Solutions:
- Traverse the given number from rightmost digit, till you get a smaller digit than the previously traversed digit. For example, if the input number is
721632, stop at1. If you do not find such a digit, then the output is-1. - At the right side of digit
1find the smallest digit greater than1. For721632, the right side of1contains632. ans digit is2. - Swap the two digits
722631. - Reverse/sort the right-side digits
631to yield722136.
def next_permutation(l):
"""implementing C++ <algorithm> next_permutation()."""
n = len(l)
if n <= 1:
return False
i = n - 1
while True:
j = i
i -= 1
if l[i] < l[j]:
k = n - 1
while not (l[i] < l[k]):
k -= 1
l[i], l[k] = l[k], l[i]
l[j:] = reversed(l[j:])
return True
if i == 0:
l.reverse()
return False
class Solution:
def nextGreaterElement(self, n: int) -> int:
l = list(str(n))
has_next = next_permutation(l)
ans = int(''.join(l))
return ans if has_next and ans < 2 ** 31 else -1
Solution: Calculate permutations
- One string will be a permutation of another string only if both of them contain the same characters with the same frequency. We can consider every possible substring/window in the long string
s2of the same length as that ofs1and check the frequency of occurrence of the characters appearing in the two. If the frequencies of every letter match exactly, then onlys1’s permutation can be a substring ofs2. - Using the sliding window approach:
from itertools import permutations
class Solution:
def nextGreaterElement(self, n: int) -> int:
all_nums_of_same_digits = [int(''.join(i)) for i in set(permutations(str(n)))]
all_nums_of_same_digits.sort()
i = all_nums_of_same_digits.index(n)
try:
return all_nums_of_same_digits[i + 1] if all_nums_of_same_digits[i + 1] <= 2**31-1 else -1
except:
return -1
[567/Medium] Permutation in String
Problem
-
Given two strings
s1ands2, return true ifs2contains a permutation ofs1, or false otherwise. In other words, return true if one ofs1’s permutations is the substring ofs2. -
Example 1:
Input: s1 = "ab", s2 = "eidbaooo"
Output: true
Explanation: s2 contains one permutation of s1 ("ba").
- Example 2:
Input: s1 = "ab", s2 = "eidboaoo"
Output: false
- Constraints:
1 <= s1.length, s2.length <= 104s1 and s2 consist of lowercase English letters.
- See problem on LeetCode.
Solution: Use counter
- One string will be a permutation of another string only if both of them contain the same characters with the same frequency. We can consider every possible substring/window in the long string
s2of the same length as that ofs1and check the frequency of occurrence of the characters appearing in the two. If the frequencies of every letter match exactly, then onlys1’s permutation can be a substring ofs2. - Using the sliding window approach:
class Solution:
def checkInclusion(self, s1: str, s2: str) -> bool:
window = len(s1)
counterS1 = Counter(s1)
for i in range(len(s2)-window + 1):
counterS2 = Counter(s2[i: i+window])
if counterS1 == counterS2:
return True
return False
Complexity
- Time: \(O(n)\). Single pass.
- Space: \(O(1)\). Constant space needed.
[665/Medium] Non-decreasing Array
Problem
-
Given an array
numswithnintegers, your task is to check if it could become non-decreasing by modifying at most one element. -
We define an array is non-decreasing if
nums[i] <= nums[i + 1]holds for everyi(0-based) such that (0 <= i <= n - 2). -
Example 1:
Input: nums = [4,2,3]
Output: true
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.
- Example 2:
Input: nums = [4,2,1]
Output: false
Explanation: You can't get a non-decreasing array by modify at most one element.
- Constraints:
n == nums.length1 <= n <= 104-105 <= nums[i] <= 105
- See problem on LeetCode.
Solution: Greedy
- Intuition:
- The one thing that we should focus on here is the fact that the problem description says non-decreasing, which is just another way of saying increasing. In this case, it means the next element must always be greater than or equal to the current element. Thus, in an array, the item on the left must be less than or equal to the item on the right. Since we can only rectify a single violation of this rule, if more than one violation exists, it is impossible to make the array non-decreasing.
- The first time we encounter such a violation i.e.
nums[i - 1] > nums[i], we make a change. You don’t actually have to make a change because the question doesn’t ask us to give the final array in order, it just asks if it could become non-decreasing. Then, we move on with the rest of the array, and continue to check for other violations. If it ever so happens that the rule gets violated again, we return false since this would be the second violation of the rule. If we don’t find a second violation, we can return true since rectifying the first violation made our array non-decreasing. - Whenever we encounter a violation at a particular index
i, we need to check what modification we can make to make the array sorted. Let’s see this scenario using an example.
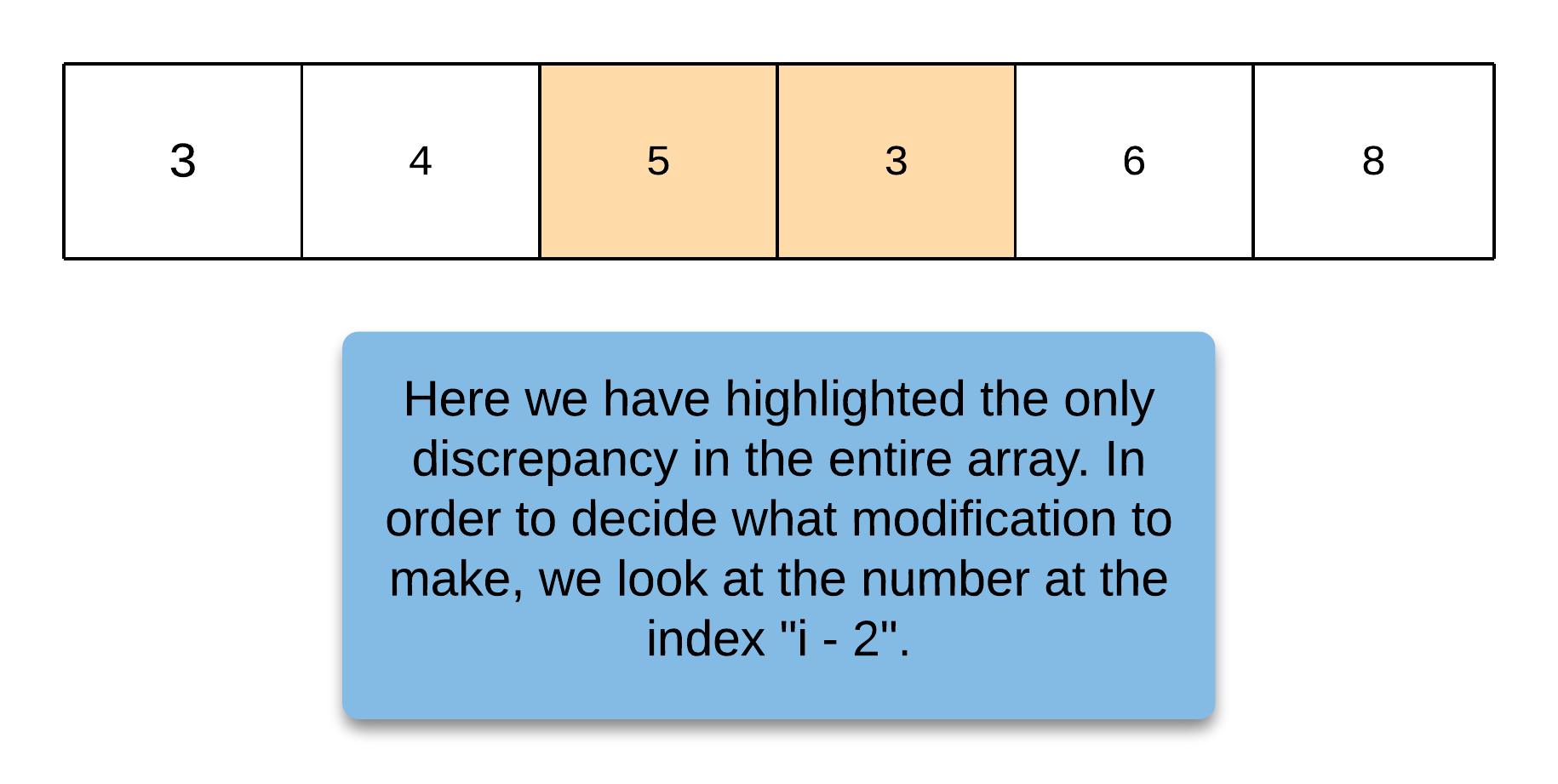
- In the example above, we consider the numbers
4, 5, 3for deciding on how to fix the violation or. In this case, the correct modification is to change the number3to5. If we change5to3, then we won’t be fixing the violation because the resulting array would be3, 4, 3, 3, 6, 8.
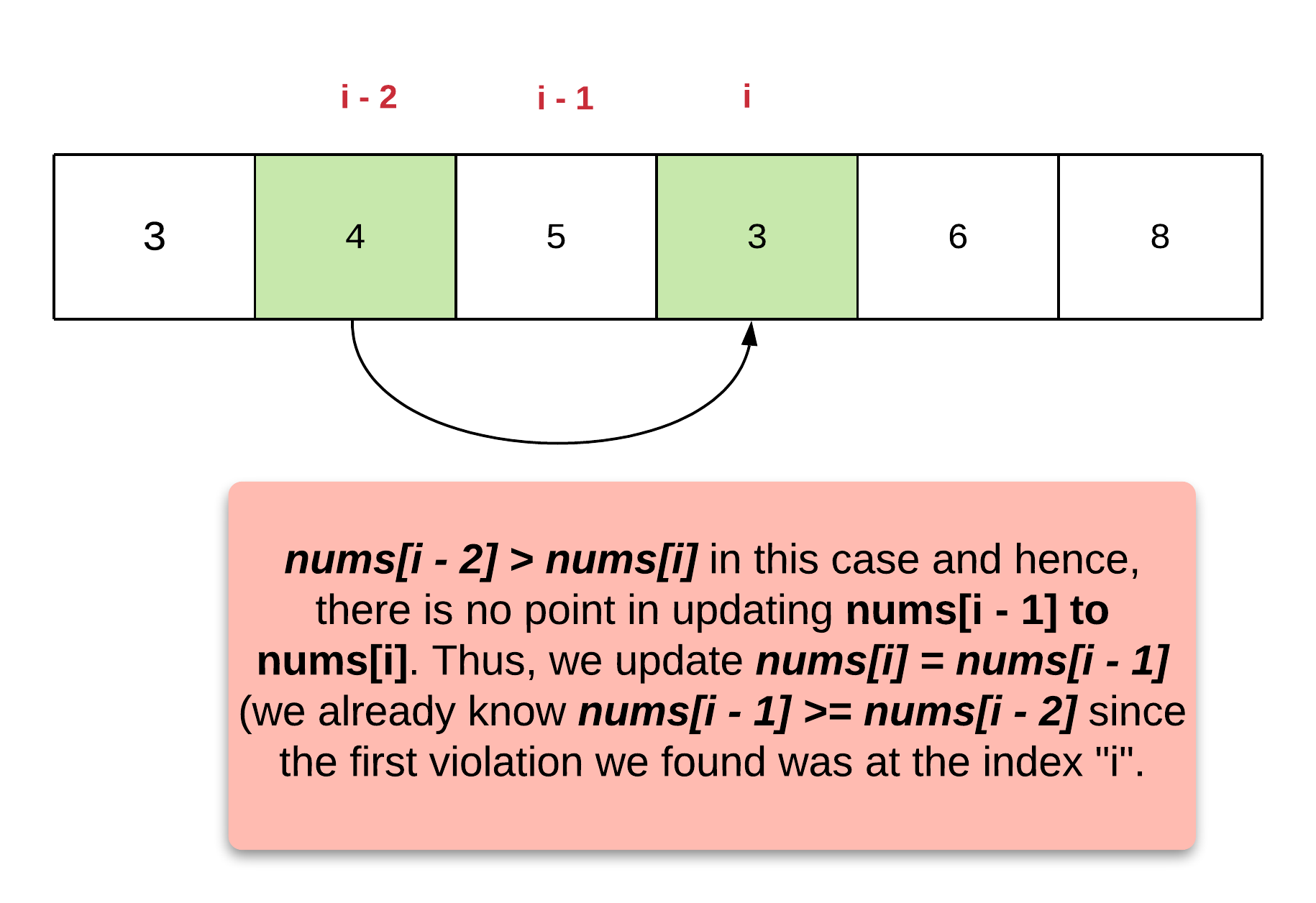
- The basic decision making process for fixing a violation is listed below. Without considering the number at the index
i - 2, we won’t be able to choose between updatingnums[i]ornums[i - 1]. The modification has to fit in with the sorted nature of the array.
if nums[i - 2] > nums[i] then nums[i] = nums[i - 1] else nums[i - 1] = nums[i]- Once we make the modification, we expect that the rest of the array will be sorted. If that is not the case, then we return false from our function. Some arrays will have violations in different places e.g. a 10 element array where
nums[4] > nums[5]and alsonums[8] > nums[9]. This array cannot be sorted by only fixing the violation atnums[5]. - Additionally, it is possible that a modification in the array leads to another violation that did not exist before. Let’s consider an example where this can happen.
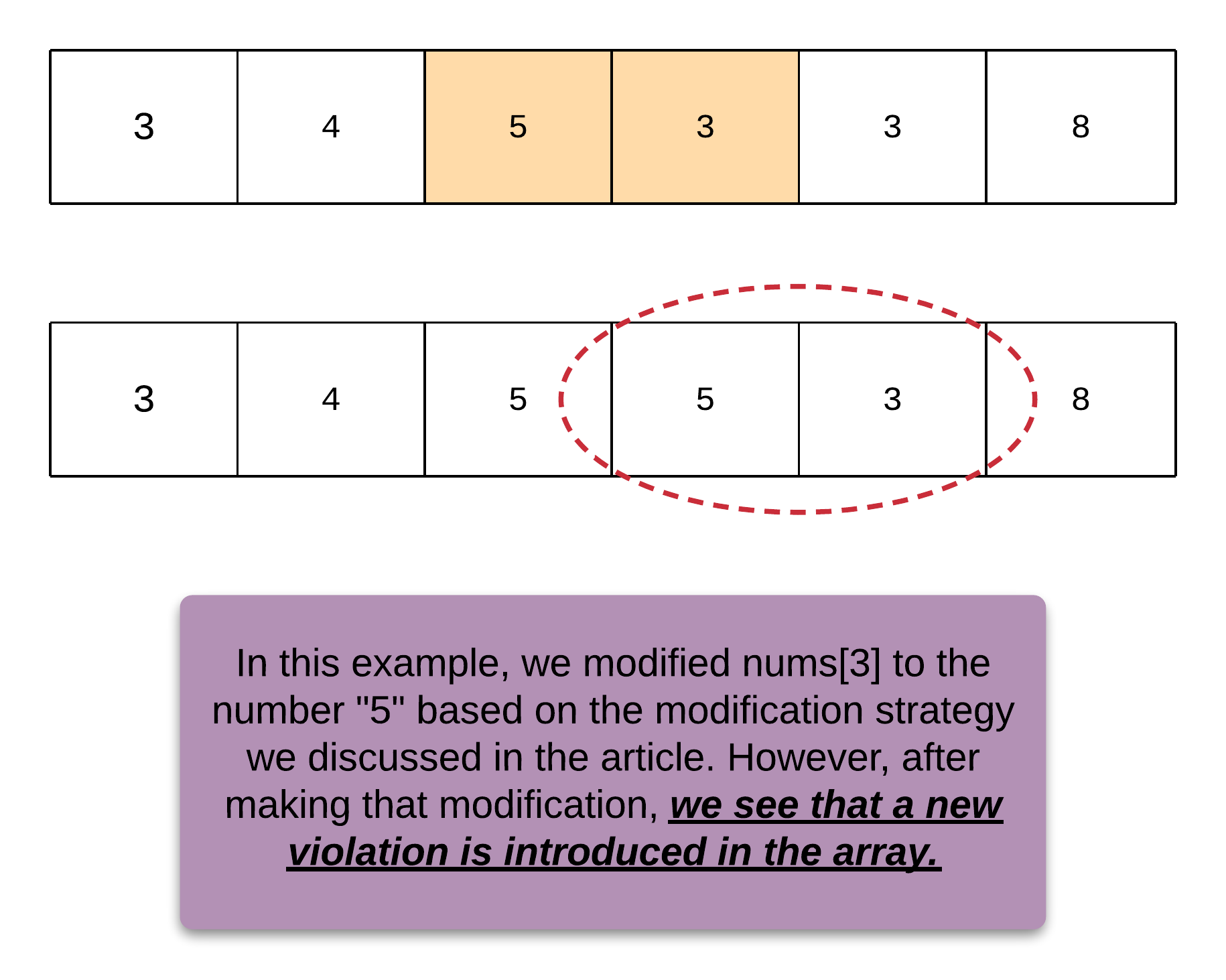
- Algorithm:
- We iterate over the array until we reach the end of the array or find a violation.
- If we reach the end of the array, we know it is sorted and we return true.
- Otherwise, we found a violation. We consider the
nums[i - 2]to fix the violation. - If the violation is at the index 1, we won’t have a
nums[i - 2]available. In that case we simply setnums[i - 1]equal tonums[i]. - Otherwise, we check if
nums[i - 2] <= nums[i]in which case we setnums[i - 1]equal tonums[i]. - Finally, if
nums[i - 2] > nums[i], then we setnums[i]equal tonums[i - 1]. - Once we make the modification, we simply iterate over the remaining array. If we find another violation, we return false. Otherwise, we return true once the iteration is complete.
class Solution:
def checkPossibility(self, nums: List[int]) -> bool:
num_violations = 0
for i in range(1, len(nums)):
if nums[i - 1] > nums[i]:
if num_violations == 1:
return False
num_violations += 1
if i < 2 or nums[i - 2] <= nums[i]:
nums[i - 1] = nums[i]
else:
nums[i] = nums[i - 1]
return True
Complexity
- Time: \(O(n)\) considering there are \(n\) elements in the array and we process each element at most once.
- Space: \(O(1)\) since we don’t use any additional space apart from a couple of variables for executing this algorithm.
[670/Medium] Maximum Swap
Problem
-
You are given an integer
num. You can swap two digits at most once to get the maximum valued number. -
Return the maximum valued number you can get.
-
Example 1:
Input: num = 2736
Output: 7236
Explanation: Swap the number 2 and the number 7.
- Example 2:
Input: num = 9973
Output: 9973
Explanation: No swap.
- Constraints:
0 <= num <= 108
- See problem on LeetCode.
Solution: Find the index of the leftmost increasing sequence
- Find a index
i, where there is a increasing order. - On the right side of
i, find the max valuemax_valand its indexmax_idx. - On the left side of
i, find the leftmost value and its indexleft_idx, which is less thanmax_val. - Swap above
left_idxandmax_idxif necessary.
class Solution:
def maximumSwap(self, num: int) -> int:
s = list(str(num)) # necessary to convert to list to mutate/swap elements
n = len(s)
for i in range(n-1): # find index where s[i] < s[i+1], meaning a chance to flip
if s[i] < s[i+1]: break
else: return num # if nothing is found, return num
max_idx, max_val = i+1, s[i+1] # keep going right, find the maximum value index
for j in range(i+1, n):
if max_val <= s[j]: max_idx, max_val = j, s[j]
left_idx = i # going right from i, find leftmost value that is less than max_val
for j in range(i, -1, -1):
if s[j] < max_val: left_idx = j
s[max_idx], s[left_idx] = s[left_idx], s[max_idx] # swap maximum after i and most left less than max
return int(''.join(s)) # re-create the integer
Complexity
- Time: \(O(n)\). Single pass.
- Space: \(O(1)\). Constant space needed.
Solution: One-pass backward iteration, track max two digits
- Iterate the list of digits backwards and keep tracking of the max digit, as well as the leftmost digit that is smaller than the max.
class Solution:
def maximumSwap(self, num: int) -> int:
# note that the conversion to a list is needed to perform the swap
# at the end (since a string is immutable/unmodifiable)
digits = list(str(num))
p, q, max_i = -1, -1, len(digits)-1
for i in range(max_i, -1, -1):
# absolute max
if digits[i] > digits[max_i]:
max_i = i
# we need the leftmost value smaller than max (hence backwards loop)
elif digits[max_i] > digits[i]:
p, q = i, max_i
# if p and q are not untouched
if p > -1 and q > -1:
# swap digits[p] and digits[q]
digits[p], digits[q] = digits[q], digits[p]
return int(''.join(digits))
Complexity
- Time: \(O(n)\). Single pass.
- Space: \(O(1)\). Constant space needed.
[674/Easy] Longest Continuous Increasing Subsequence/Subarray
Problem
-
Given an unsorted array of integers
nums, return the length of the longest continuous increasing subsequence (i.e. subarray). The subsequence must be strictly increasing. -
A continuous increasing subsequence is defined by two indices
landr(l < r) such that it is[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]and for eachl <= i < r,nums[i] < nums[i + 1]. -
Example 1:
Input: nums = [1,3,5,4,7]
Output: 3
Explanation: The longest continuous increasing subsequence is [1,3,5] with length 3.
Even though [1,3,5,7] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.
- Example 2:
Input: nums = [2,2,2,2,2]
Output: 1
Explanation: The longest continuous increasing subsequence is [2] with length 1. Note that it must be strictly
increasing.
- Constraints:
1 <= nums.length <= 104-109 <= nums[i] <= 109
- See problem on LeetCode.
Solution: Loop over each operation, process it, append outcome to a list
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if not nums:
return 0
curLen = 1
maxLen = 1
for i in range(1, len(nums)):
if nums[i] > nums[i-1]:
curLen += 1
else:
curLen = 1
maxLen = max(maxLen, curLen)
return maxLen
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[681/Medium] Next Closest Time
Problem
-
Given a time represented in the format
"HH:MM", form the next closest time by reusing the current digits. There is no limit on how many times a digit can be reused. -
You may assume the given input string is always valid. For example,
"01:34","12:09"are all valid."1:34","12:9"are all invalid. -
Example 1:
Input: time = "19:34"
Output: "19:39"
Explanation: The next closest time choosing from digits 1, 9, 3, 4, is 19:39, which occurs 5 minutes later.
It is not 19:33, because this occurs 23 hours and 59 minutes later.
- Example 2:
Input: time = "23:59"
Output: "22:22"
Explanation: The next closest time choosing from digits 2, 3, 5, 9, is 22:22.
It may be assumed that the returned time is next day's time since it is smaller than the input time numerically.
- Constraints:
time.length == 5time is a valid time in the form "HH:MM".0 <= HH < 240 <= MM < 60
- See problem on LeetCode.
Solution: Loop over each operation, process it, append outcome to a list
class Solution:
def nextClosestTime(self, time: str) -> str:
hour, minute = time.split(':')
# generate sorted permutations of the input digits
# in both hour and minute
nums = sorted(set(hour+minute))
all_time = [a+b for a in nums for b in nums]
# the only change needed is minutes
# hour remains the same
i = all_time.index(minute)
if i+1 < len(all_time) and all_time[i+1] < '60':
return hour+':'+all_time[i+1]
# we need to change both the hour and minute
# change minutes to the smallest value available
# change hour to the next value available
# for e.g., 12:59 -> 15:11
i = all_time.index(hour)
if i+1 < len(all_time) and all_time[i+1] < '24':
return all_time[i+1]+':'+all_time[0]
# it's not possible to find another time in the same day
# so find the smallest in the next day
# for e.g., 23:59 -> 22:22
return all_time[0]+':'+all_time[0]
Complexity
- Time: \(O(1)\)
- Space: \(O(perm(n+m))\) where \(n\) is the average number of unique digits in the hour and \(m\) is the average number of unique digits in the minute
- Assuming the worst case of all unique digits in the hour and number, n+m = 4, so perm(4) = 4! = 24 so \(O(24) = O(1)\)
[682/Easy] Baseball Game
Problem
-
You are keeping score for a baseball game with strange rules. The game consists of several rounds, where the scores of past rounds may affect future rounds’ scores.
-
At the beginning of the game, you start with an empty record. You are given a list of strings
ops, whereops[i]is thei-thoperation you must apply to the record and is one of the following:- An integer
x- Record a new score ofx. "+"- Record a new score that is the sum of the previous two scores. It is guaranteed there will always be two previous scores."D"- Record a new score that is double the previous score. It is guaranteed there will always be a previous score."C"- Invalidate the previous score, removing it from the record. It is guaranteed there will always be a previous score.
- An integer
-
Return the sum of all the scores on the record.
-
Example 1:
Input: ops = ["5","2","C","D","+"]
Output: 30
Explanation:
"5" - Add 5 to the record, record is now [5].
"2" - Add 2 to the record, record is now [5, 2].
"C" - Invalidate and remove the previous score, record is now [5].
"D" - Add 2 * 5 = 10 to the record, record is now [5, 10].
"+" - Add 5 + 10 = 15 to the record, record is now [5, 10, 15].
The total sum is 5 + 10 + 15 = 30.
- Example 2:
Input: ops = ["5","-2","4","C","D","9","+","+"]
Output: 27
Explanation:
"5" - Add 5 to the record, record is now [5].
"-2" - Add -2 to the record, record is now [5, -2].
"4" - Add 4 to the record, record is now [5, -2, 4].
"C" - Invalidate and remove the previous score, record is now [5, -2].
"D" - Add 2 * -2 = -4 to the record, record is now [5, -2, -4].
"9" - Add 9 to the record, record is now [5, -2, -4, 9].
"+" - Add -4 + 9 = 5 to the record, record is now [5, -2, -4, 9, 5].
"+" - Add 9 + 5 = 14 to the record, record is now [5, -2, -4, 9, 5, 14].
The total sum is 5 + -2 + -4 + 9 + 5 + 14 = 27.
- Example 3:
Input: ops = ["1"]
Output: 1
- Constraints:
1 <= ops.length <= 1000ops[i] is "C", "D", "+", or a string representing an integer in the range [-3 * 104, 3 * 104].For operation "+", there will always be at least two previous scores on the record.For operations "C" and "D", there will always be at least one previous score on the record.
- See problem on LeetCode.
Solution: Loop over each operation, process it, append outcome to a list
class Solution:
def calPoints(self, ops: List[str]) -> int:
res = []
for op in ops:
if op.isdigit():
res.append(int(op))
elif op == 'C':
res = res[:-1]
elif op == 'D':
res = int(res[-1])
res.append(double*2)
elif op == '+':
s = int(res[-1] + res[-2])
res.append(s)
else:
res.append(int(op[1:])*-1)
return sum(res)
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for
res
[683/Hard] K Empty Slots
Problem
-
You have
nbulbs in a row numbered from1 to n. Initially, all the bulbs are turned off. We turn on exactly one bulb every day until all bulbs are on after n days. -
You are given an array bulbs of length
nwherebulbs[i] = xmeans that on the(i+1)thday, we will turn on the bulb at positionxwhereiis0-indexedandxis1-indexed. -
Given an integer
k, return the minimum day number such that there exists two turned on bulbs that have exactlykbulbs between them that are all turned off. If there isn’t such day, return-1. -
Example 1:
Input: bulbs = [1,3,2], k = 1
Output: 2
Explanation:
On the first day: bulbs[0] = 1, first bulb is turned on: [1,0,0]
On the second day: bulbs[1] = 3, third bulb is turned on: [1,0,1]
On the third day: bulbs[2] = 2, second bulb is turned on: [1,1,1]
We return 2 because on the second day, there were two on bulbs with one off bulb between them.
- Example 2:
Input: bulbs = [1,2,3], k = 1
Output: -1
- Constraints:
n == bulbs.length1 <= n <= 2 * 1041 <= bulbs[i] <= nbulbs is a permutation of numbers from 1 to n.0 <= k <= 2 * 104
- See problem on LeetCode.
Solution
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for
res
[686/Medium] Repeated String Match
Problem
-
Given two strings
aandb, return the minimum number of times you should repeat stringaso that stringbis a substring of it. If it is impossible forbto be a substring of a after repeating it, return-1. -
Notice: string
"abc"repeated 0 times is"", repeated 1 time is"abc"and repeated 2 times is"abcabc". -
Example 1:
Input: a = "abcd", b = "cdabcdab"
Output: 3
Explanation: We return 3 because by repeating a three times "abcdabcdabcd", b is a substring of it.
- Example 2:
Input: a = "a", b = "aa"
Output: 2
- Constraints:
1 <= a.length, b.length <= 104a and b consist of lowercase English letters.
- See problem on LeetCode.
Solution:
- In order for
bto be ina,a’s length must be no less thanb’s. And hence we need to bottom the multiplier tox(i.e.,n // m) in order fora’s length to reachb. - On the other side, at most we multiply
aby(x + 2)and then we can easily tell whetherbcan be part of a or not. It’s easy to tell in the first example:a = "abcd",b = "cdabcdab", we need to add'head'and'tail'toa, and hencex + 2. Ifbis not ina * (x + 2), then there’s no need to further expanda. - Examples:
- Consider A =
'abc'and B ='abcabcabc':len(B)/len(A) = 3. However, you cannot dorange(1,3), you will needrange(1,4). So this causes us to need at the minimumint(len(B)/len(A)) + 1. - Consider A =
'abc'and B ='abcabcab': Now you getint(len(B)/len(A)) = 2and we will still needrange(1,4)so it will be int(len(B)/len(A)) + 2 because it rounded down. So we will need at least +2 to be safe so far. - Finally, consider the worst case scenario with residual characters in the front and beginning. A =
'abc'and B ='cabcabca': In this case we will need to buffer in front and at the end because of how the string starts and ends (starts with c and ends with a). We getint(len(B)/len(A)) = 2. However we will need 4 copies of A to cover B: ab[cabcabca]bc. This means we needrange(1,5)which means we will needint(len(B)/len(A)) + 3. This is definitely the worst case scenario because aside from the start and finish of B both needing extra copies, the rounding down, and therange(N)only going up toN-1there is no other way to create a worse situation.
- Consider A =
-
Here,
repeatStringisawhilefindStringisb. - Similar approach; rehashed:
class Solution:
def repeatedStringMatch(self, a: str, b: str) -> int:
m, n = len(a), len(b)
x = n // m
inc = [0, 1, 2]
for i in inc:
if b in a * (x + i):
return x + i
return -1
class Solution:
def repeatedStringMatch(self, repeatString: str, findString: str) -> int:
x = len(findString) // len(repeatString)
if findString in repeatString*x:
return a
elif findString in repeatString*(x+1):
return x+1
elif findString in repeatString*(x+2):
return x+2
return -1
[708/Medium] Insert into a Sorted Circular Linked List
Problem
-
Given a Circular Linked List node, which is sorted in ascending order, write a function to insert a value
insertValinto the list such that it remains a sorted circular list. The given node can be a reference to any single node in the list and may not necessarily be the smallest value in the circular list. -
If there are multiple suitable places for insertion, you may choose any place to insert the new value. After the insertion, the circular list should remain sorted.
-
If the list is empty (i.e., the given node is
null), you should create a new single circular list and return the reference to that single node. Otherwise, you should return the originally given node. -
Example 1:
Input: head = [3,4,1], insertVal = 2
Output: [3,4,1,2]
Explanation: In the figure above, there is a sorted circular list of three elements. You are given a reference to the node with value 3, and we need to insert 2 into the list. The new node should be inserted between node 1 and node 3. After the insertion, the list should look like this, and we should still return node 3.
- Example 2:
Input: head = [], insertVal = 1
Output: [1]
Explanation: The list is empty (given head is null). We create a new single circular list and return the reference to that single node.
- Example 3:
Input: head = [1], insertVal = 0
Output: [1,0]
- Constraints:
The number of nodes in the list is in the range [0, 5 * 104].-106 <= Node.val, insertVal <= 106
Solution: Iteration (One-pass)
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, next=None):
self.val = val
self.next = next
"""
class Solution:
def insert(self, head: 'Node', insertVal: int) -> 'Node':
#edge cases
if not head:
node = Node(insertVal)
node.next = node
return node
curr = head
while curr.next != head:
#insert in the normal position
if curr.val <= insertVal <= curr.next.val:
break
#insert in the link position
if curr.val > curr.next.val and (curr.val <= insertVal or insertVal <= curr.next.val):
break
curr = curr.next
#insert new nodes
insert_node = Node(insertVal, next=curr.next)
curr.next = insert_node
return head
[766/Easy] Toeplitz Matrix
Problem
-
Given an
m x nmatrix, returntrueif the matrix is Toeplitz. Otherwise, returnfalse. -
A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.
-
Example 1:
Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
Output: true
Explanation:
In the above grid, the diagonals are:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]".
In each diagonal all elements are the same, so the answer is True.
- Example 2:
Input: matrix = [[1,2],[2,2]]
Output: false
Explanation:
The diagonal "[1, 2]" has different elements.
- Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200 <= matrix[i][j] <= 99
- See problem on LeetCode.
Solution: DP
class Solution:
def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:
d = {}
for i in range(len(matrix)):
for j in range(len(matrix[0])):
if i - j in d and d[i-j] != matrix[i][j]:
return False
else: d[i-j] = matrix[i][j]
return True
Complexity
- Time: \(O(n*m)\)
- Space: \(O(n + m - 1)\)
Solution: One-loop
class Solution:
def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:
for r1, r2 in zip(matrix[:-1], matrix[1:]):
if r1[:-1] != r2[1:]:
return False
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: One-liner
class Solution:
def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:
return all(r1[:-1] == r2[1:] for r1, r2 in zip(matrix[:-1], matrix[1:]))
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[771/Easy] Jewels and Stones
Problem
- You’re given strings
jewelsrepresenting the types of stones that are jewels, andstonesrepresenting the stones you have. Each character instonesis a type of stone you have. You want to know how many of the stones you have are also jewels. -
Letters are case sensitive, so
"a"is considered a different type of stone from"A". - Example 1:
Input: jewels = "aA", stones = "aAAbbbb"
Output: 3
- Example 2:
Input: jewels = "z", stones = "ZZ"
Output: 0
- Constraints:
1 <= jewels.length, stones.length <= 50jewels and stones consist of only English letters.All the characters of jewels are unique.
- See problem on LeetCode.
Solution
class Solution:
def numJewelsInStones(self, jewels: str, stones: str) -> int:
return sum(s in jewels for s in stones)
- Same approach; rehashed:
class Solution:
def numJewelsInStones(self, jewels: str, stones: str) -> int:
count = 0
for i in stones:
if i in jewels:
count+=1
return count
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[778/Hard] Swim in Rising Water
Problem
-
You are given an
n x ninteger matrix grid where each valuegrid[i][j]represents the elevation at that point(i, j). -
The rain starts to fall. At time
t, the depth of the water everywhere ist. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at mostt. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim. -
Return the least time until you can reach the bottom right square
(n - 1, n - 1)if you start at the top left square(0, 0). -
Example 1:

Input: grid = [[0,2],[1,3]]
Output: 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.
- Example 2:
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation: The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
- Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 500 <= grid[i][j] < n2Each value grid[i][j] is unique.
- See problem on LeetCode.
Solution: Dijkstra Algorithm + Min Heap
-
This problem is about finding the shortest path from top-left point, for i.e., index
(0,0)to bottom-right point i.e, index(n-1, n-1). Dijkstra’s algorithm can be used to solve the single-source shortest-paths problem on a weighted, directed graphG = (V,E)for the case in which all edge weights are positive. -
In our case the weight between two nodes is the max of cell value of both nodes. For example if
Node1has a value of 3 andNode2has a value of 2, then weight between those will bemax(3,2) = 3. Also when moving from one vertex/Node to another, instead of adding their weights we will take only the maximum one because travel time is given as 0. -
We will use Min Heap to implement Dijkstra algorithm. For Min Heap we will use
heapqmodule. We will also create a class to represent a Node.
import heapq
class Node:
def __init__(self, x, y, val):
# (x,y) position of node in grid
self.x = x
self.y = y
# value of node. Will represent its weight
self.val = val
# We need this so that we can push Node object into out heap
def __lt__(self, other):
return self.val < other.val
# Just a wrapper to use heapq in Object Oriented Programming way
class MinHeap:
def __init__(self):
self.heap = []
def push(self, node):
heapq.heappush(self.heap, node)
def pop(self) -> Node:
return heapq.heappop(self.heap)
- Now to start solving we will push the node at index
(0,0)to Min Heap and start our loop. - We will also keep a 2D List to track which nodes we have already visited. You can instead make this a property of the node if you want instead of creating a new List.
- We will loop until we have not visited the node at
(n-1, n-1). - We will first pop out the minimum node from Min Heap; update our time taken and push all its unvisited neighbors into the heap.
- Finally our time taken will be the result.
class Solution:
def swimInWater(self, grid: List[List[int]]) -> int:
n = len(grid)
# Our 2D List to track which Nodes have been visited
visited = [[False]*n for _ in range(n)]
# Time taken. Initialised to grid[0][0] because we can't move from
# there unless time taken is atleast same as this
# Suppose grid[0][0] is 3, then we cannot move unless t = 3
t = grid[0][0]
# Our MinHeap with initial element as Node at index (0,0)
minHeap = MinHeap()
minHeap.push(Node(0, 0, grid[0][0]))
# Loop until we haven't visited the Node at (n-1, n-1)
while not visited[n-1][n-1] and minHeap:
# Get the Node with smallest value
node = minHeap.pop()
# Update its visited status
visited[node.x][node.y] = True
# Update the time taken
t = max(t, node.val)
# Push the neighbors of current node into the heap
# Make sure to check their visited status first
if node.y > 0 and not visited[node.x][node.y-1]: # Above Node
minHeap.push(Node(node.x, node.y-1, grid[node.x][node.y-1]))
if node.x > 0 and not visited[node.x-1][node.y]: # Left Node
minHeap.push(Node(node.x-1, node.y, grid[node.x-1][node.y]))
if node.y < n-1 and not visited[node.x][node.y+1]: # Below Node
minHeap.push(Node(node.x, node.y+1, grid[node.x][node.y+1]))
if node.x < n-1 and not visited[node.x+1][node.y]: # Right Node
minHeap.push(Node(node.x+1, node.y, grid[node.x+1][node.y]))
return t
Solution: Binary Search on Time/Height
-
At time ‘t’, there are t units/height of water, i.e.., each building will have a minimum height of ‘t’ due to rain water. In other words, we will be able to reach a height ‘t’ only at ‘t’ hours, not before that.
-
Also, it is given that if we have a path with height <= t at time ‘t’ from [0,0] to [n-1,m-1], we can reach from start to end in negligible amount of time.
-
So, basically for this problem time is not an issue for traveling, but we need to wait for a certain time to reach a building of height h > t.
Thus, we can perform a binary search on the minimum amount of time we need to wait, such that a path is available between [0,0] and [n-1,m-1] and all the building in the path are of height <= t.
- Now, What should be the range of our Binary Search?
- Initially we are at time 0, so left bound is 0. And max amount of time we need to wait can be the max height of the given buildings in the grid (in worst case), so max height of the buildings in the grid is our right bound for binary search.
- Now, we need to perform binary search, for minimum height for which there is a path from [0,0] to [n-1,m-1].
- How do we know that a path exists?
- Simply by performing Depth First Traversal.
- Here, we will travel in all the four directions (up, down, left, right) by not visiting the node we have visited earlier. And in this traversal we start from [0,0] and if we happen to touch [n-1,m-1], then we can say that a path exists.
- This is general Depth First Traversal, but we have another constraint that we cannot move to a height > t, so we include a constraint that we can move in any of the four directions, if and only if, the height of the building in that direction is less than ‘t’.
- Binary Search Idea:
- If at time ‘t’, we found a path, it means there is a possibility that a path may exist at time < t. So, we again search in the boundary [0, t].
- If at time ‘t’, we did not find a path, it means definitely there is no path in time <= t. So, we need to search in the boundary [t+1, max height of buildings in grid].
class Solution:
def swimInWater(self, grid: List[List[int]]) -> int:
def PathSearch(height, i, j, visited):
if not visited[i][j] and grid[i][j] <= height:
visited[i][j] = 1
if i-1 >= 0:
PathSearch(height, i-1, j, visited)
if i+1 < n:
PathSearch(height, i+1, j, visited)
if j-1 >= 0:
PathSearch(height, i, j-1, visited)
if j+1 < n:
PathSearch(height, i, j+1, visited)
def BinarySearch(l, r):
while l < r:
mid = (l+r)//2
visited = [[0]*m for _ in range(n)]
PathSearch(mid, 0, 0, visited)
if visited[n-1][m-1]:
r = mid
else:
l = mid + 1
return l
n, m = len(grid), len(grid[0])
l, r = 0, max(max(x) for x in grid)
return BinarySearch(l, r)
- For this Case, we have a square grid, so N == M.
Complexity
- Time: \(O(N * N)\) for Depth First Traversal and \(O(log (50 * 50 -1))\) for Binary Search which is constant \(= O(N^2)\)
- Why
50 * 50 -1? -> AsN = 50and the0<=grid[i][j]<=N * N - 1. So, instead of calculating the right bound = max height of the buildings in grid, we can also make the right bound as50 * 50 - 1. - For some people, they would not like to consider
N * N - 1as constant. As even though it is small, but it is still variable. (It is a debatable topic). - So for them, Time: \(O(N^2) * O(log(N^2)) = O(N^2) * 2 * O(logN) = O(N^2 log N)\).
- Why
- Space: \(O(4 * N * N)\) owing to the Depth First Traversal Recursion Tree + \(O(N * M)\) for the visited array = \(O (N^2)\) overall.
[791/Medium] Custom Sort String
Problem
- You are given two strings
orderands. All the characters oforderare unique and were sorted in some custom order previously. - Permute the characters of
sso that they match the order thatorderwas sorted. More specifically, if a characterxoccurs before a characteryin order, thenxshould occur beforeyin the permuted string. - Return any permutation of
sthat satisfies this property. - Example 1:
Input: order = "cba", s = "abcd"
Output: "cbad"
Explanation:
"a", "b", "c" appear in order, so the order of "a", "b", "c" should be "c", "b", and "a".
Since "d" does not appear in order, it can be at any position in the returned string. "dcba", "cdba", "cbda" are also valid outputs.
- Example 2:
Input: order = "cbafg", s = "abcd"
Output: "cbad"
- Constraints:
1 <= order.length <= 261 <= s.length <= 200 order and s consist of lowercase English letters.All the characters of order are unique.
- See problem on LeetCode.
Solution: Build up result by looping over order and checking for chars in string; then add chars not in order to the answer
- For each character in
order, add the number of occurrences of that character instrtoans. - Write to
ansall other letters fromstr, that is not inorder.
class Solution:
def customSortString(self, order: str, s: str) -> str:
ans = ""
for c in order:
ans += c * s.count(c)
for c in s:
if c not in order:
ans += c
return ans
Complexity
- Time: \(O(m + n)\), where
m= length of order andn= length of str. - Space: \(O(1)\)
[792/Medium] Number of Matching Subsequences
Problem
- Given a string
sand an array of stringswords, return the number ofwords[i]that is a subsequence ofs. - A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
- For example,
"ace"is a subsequence of"abcde".
- For example,
- Example 1:
Input: s = "abcde", words = ["a","bb","acd","ace"]
Output: 3
Explanation: There are three strings in words that are a subsequence of s: "a", "acd", "ace".
- Example 2:
Input: s = "dsahjpjauf", words = ["ahjpjau","ja","ahbwzgqnuk","tnmlanowax"]
Output: 2
- Constraints:
1 <= s.length <= 5 * 1041 <= words.length <= 50001 <= words[i].length <= 50s and words[i] consist of only lowercase English letters.
- See problem on LeetCode.
Solution: Build up result by looping over order and checking for chars in string; then add chars not in order to the answer
- For each character in
order, add the number of occurrences of that character instrtoans. - Write to
ansall other letters fromstr, that is not inorder.
class Solution:
def numMatchingSubseq(self, s: str, words: List[str]) -> int:
def isSubSeq(word):
index =- 1
for char in word:
# update index, always start index+1 to ensure
# you don't reuse the prior found character
# note that str.find() returns the index of first occurrence of the substring if found. If not found, it returns -1.
# the syntax of find() is: str.find(sub[, start[, end]])
# str.index() is almost the same as str.find(), the only difference is that str.index() raises an exception if the value is not found.
index = s.find(char, index+1)
if index == -1:
return False
return True
count = 0
for word in words:
if isSubSeq(word):
count+=1
return count
Complexity
- Time: \(O(m + n)\), where
m= length of order andn= length of str. - Space: \(O(1)\)
[796/Easy] Rotate String
Problem
-
Given two strings
sandgoal, returntrueif and only ifscan becomegoalafter some number of shifts ons. - A shift on
sconsists of moving the leftmost character ofsto the rightmost position.- For example, if
s = "abcde", then it will be"bcdea"after one shift.
- For example, if
- Example 1:
Input: s = "abcde", goal = "cdeab"
Output: true
- Example 2:
Input: s = "abcde", goal = "abced"
Output: false
- Constraints:
1 <= s.length, goal.length <= 100s and goal consist of lowercase English letters.
- See problem on LeetCode.
Solution
class Solution:
def rotateString(self, s: str, goal: str) -> bool:
if len(s) != len(goal):
return False
return goal in s + s
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[953/Easy] Verifying an Alien Dictionary/Mapping to Normal Order
Problem
-
In an alien language, surprisingly, they also use English lowercase letters, but possibly in a different
order. Theorderof the alphabet is some permutation of lowercase letters. -
Given a sequence of
wordswritten in the alien language, and theorderof the alphabet, returntrueif and only if the givenwordsare sorted lexicographically in this alien language. -
Example 1:
Input: words = ["hello","leetcode"], order = "hlabcdefgijkmnopqrstuvwxyz"
Output: true
Explanation: As 'h' comes before 'l' in this language, then the sequence is sorted.
- Example 2:
Input: words = ["word","world","row"], order = "worldabcefghijkmnpqstuvxyz"
Output: false
Explanation: As 'd' comes after 'l' in this language, then words[0] > words[1], hence the sequence is unsorted.
- Example 3:
Input: words = ["apple","app"], order = "abcdefghijklmnopqrstuvwxyz"
Output: false
Explanation: The first three characters "app" match, and the second string is shorter (in size.) According to lexicographical rules "apple" > "app", because 'l' > '∅', where '∅' is defined as the blank character which is less than any other character ([More info](https://en.wikipedia.org/wiki/Lexicographical_order)).
- See problem on LeetCode.
Solution
- Method 1:
def isAlienSorted(self, words: List, order: str):
m = {c: i for i, c in enumerate(order)}
words = [[m[c] for c in w] for w in words]
return all(w1 <= w2 for w1, w2 in zip(words, words[1:]))
- Method 2 (one-liner):
# slow, just for fun
def isAlienSorted(self, words: List, order: str):
return words == sorted(words, key=lambda w: map(order.index, w))
Complexity
- Time: \(O(S_1S_2)\) where \(S_1\) and \(S_2\) are the input strings
- Space: \(O(1)\)
[989/Easy] Add to Array-Form of Integer
Problem
- The array-form of an integer
numis an array representing its digits in left to right order. - For example, for
num = 1321, the array form is[1,3,2,1]. -
Given
num, the array-form of an integer, and an integerk, return the array-form of the integernum + k. - Example 1:
Input: num = [1,2,0,0], k = 34
Output: [1,2,3,4]
Explanation: 1200 + 34 = 1234
- Example 2:
Input: num = [2,7,4], k = 181
Output: [4,5,5]
Explanation: 274 + 181 = 455
- Example 3:
Input: num = [2,1,5], k = 806
Output: [1,0,2,1]
Explanation: 215 + 806 = 1021
- Constraints:
1 <= num.length <= 1040 <= num[i] <= 9numdoes not contain any leading zeros except for the zero itself.1 <= k <= 104
Solution: Stringify, convert to int and then add
class Solution:
def addToArrayForm(self, num: List[int], k: int) -> List[int]:
val = ''.join([str(n) for n in num])
ans = int(val) + k
return list(str(ans))
Complexity
- Time: \(O(n + n) = O(n)\)
- Space: \(O(1)\)
[1108/Easy] Defanging an IP Address
Problem
-
Given a valid (IPv4) IP
address, return a defanged version of that IP address. -
A defanged IP address replaces every period
"."with"[.]". -
Example 1:
Input: address = "1.1.1.1"
Output: "1[.]1[.]1[.]1"
- Example 2:
Input: address = "255.100.50.0"
Output: "255[.]100[.]50[.]0"
- Constraints:
The given address is a valid IPv4 address.
- See problem on LeetCode.
Solution
class Solution:
def defangIPaddr(self, address: str) -> str:
return address.replace(".","[.]")
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) since
str.replace()returns a new string
[1111/Medium] Maximum Nesting Depth of Two Valid Parentheses Strings
Problem
- A string is a valid parentheses string (denoted VPS) if and only if it consists of
"("and")"characters only, and:- It is the empty string, or
- It can be written as
AB(A concatenated with B), whereAandBare VPS’s, or - It can be written as (
A), whereAis a VPS.
- We can similarly define the nesting depth
depth(S)of any VPSSas follows:depth("") = 0depth(A + B) = max(depth(A), depth(B)), whereAandBare VPS’sdepth("(" + A + ")") = 1 + depth(A), whereAis a VPS.`
- For example,
"","()()", and"()(()())"are VPS’s (with nesting depths 0, 1, and 2), and")("and"(()"are not VPS’s. - Given a VPS seq, split it into two disjoint subsequences
AandB, such thatAandBare VPS’s (andA.length + B.length = seq.length). - Now choose any such
AandBsuch thatmax(depth(A), depth(B))is the minimum possible value. -
Return an
answerarray (of lengthseq.length) that encodes such a choice ofAandB:answer[i] = 0 if seq[i]is part ofA, elseanswer[i] = 1. Note that even though multiple answers may exist, you may return any of them. - Example 1:
Input: seq = "(()())"
Output: [0,1,1,1,1,0]
- Example 2:
Input: seq = "()(())()"
Output: [0,0,0,1,1,0,1,1]
- See problem on LeetCode.
Solution:
class Solution:
def maxDepthAfterSplit(self, seq: str) -> List[int]:
left = 0
right = 0
res = []
for paren in seq:
if paren == "(":
res.append(left)
# alternate between 0 and 1
left = 1-left
elif paren == ")":
res.append(right)
# alternate between 0 and 1
right = 1-right
return res
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for
res
[1268/Medium]
Problem
-
You are given an array of strings
productsand a stringsearchWord. -
Design a system that suggests at most three product names from products after each character of searchWord is typed. Suggested products should have common prefix with
searchWord. If there are more than three products with a common prefix return the three lexicographically minimums products. -
Return a list of lists of the suggested products after each character of searchWord is typed.
-
Example 1:
Input: products = ["mobile","mouse","moneypot","monitor","mousepad"], searchWord = "mouse"
Output: [
["mobile","moneypot","monitor"],
["mobile","moneypot","monitor"],
["mouse","mousepad"],
["mouse","mousepad"],
["mouse","mousepad"]
]
Explanation: products sorted lexicographically = ["mobile","moneypot","monitor","mouse","mousepad"]
After typing m and mo all products match and we show user ["mobile","moneypot","monitor"]
After typing mou, mous and mouse the system suggests ["mouse","mousepad"]
- Example 2:
Input: products = ["havana"], searchWord = "havana"
Output: [["havana"],["havana"],["havana"],["havana"],["havana"],["havana"]]
- Example 3:
Input: products = ["bags","baggage","banner","box","cloths"], searchWord = "bags"
Output: [["baggage","bags","banner"],["baggage","bags","banner"],["baggage","bags"],["bags"]]
- Constraints:
1 <= products.length <= 10001 <= products[i].length <= 30001 <= sum(products[i].length) <= 2 * 104All the strings of products are unique.products[i] consists of lowercase English letters.1 <= searchWord.length <= 1000searchWord consists of lowercase English letters.
- See problem on LeetCode.
Solution: Look for prefixes incrementally, find words that start with them and return the top 3
class Solution:
def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:
result = []
products.sort()
for x in range(len(searchWord)):
word = searchWord[:x+1]
products = [item for item in products if item.startswith(word)]
result.append(products[:3])
return result
Complexity
- Time: \(O(n\log{n})\) where \(n\) is the length of
products - Space: \(O(1)\) excluding output space required for
result
[1288/Medium] Remove Covered Intervals
Problem
-
Given an array intervals where
intervals[i] = [l_i, r_i]represent the interval[l_i, r_i), remove all intervals that are covered by another interval in the list. -
The interval
[a, b)is covered by the interval[c, d)if and only ifc <= a and b <= d. -
Return the number of remaining intervals.
-
Example 1:
Input: intervals = [[1,4],[3,6],[2,8]]
Output: 2
Explanation: Interval [3,6] is covered by [2,8], therefore it is removed.
- Example 2:
Input: intervals = [[1,4],[2,3]]
Output: 1
- Constraints:
1 <= intervals.length <= 1000intervals[i].length == 20 <= l_i < r_i <= 105All the given intervals are unique.
- See problem on LeetCode.
Solution: Sort start point by ascending order, end point by descending order; for interval overlaps, check if the current interval’s end point is less than or equal than previous interval’s end point
- Greedy Algorithm:
- The idea of greedy algorithm is to pick the locally optimal move at each step, which would lead to the globally optimal solution.
- Typical greedy solution has \(\mathcal{O}(n \log n)\) time complexity and consists of two steps:
- Figure out how to sort the input data. That would take \(\mathcal{O}(n \log n)\) time, and could be done directly by sorting or indirectly by using heap data structure. Usually sorting is better than heap usage because of gain in space.
- Parse the sorted input in \(\mathcal{O}(n)\) time to construct a solution.
- In the case of already sorted input, the greedy solution could have \(\mathcal{O}(n)\) time complexity, here is an example.
- Intuition:
- Let us figure out how to sort the input. The idea to sort by start point is pretty obvious, because it simplifies further parsing:
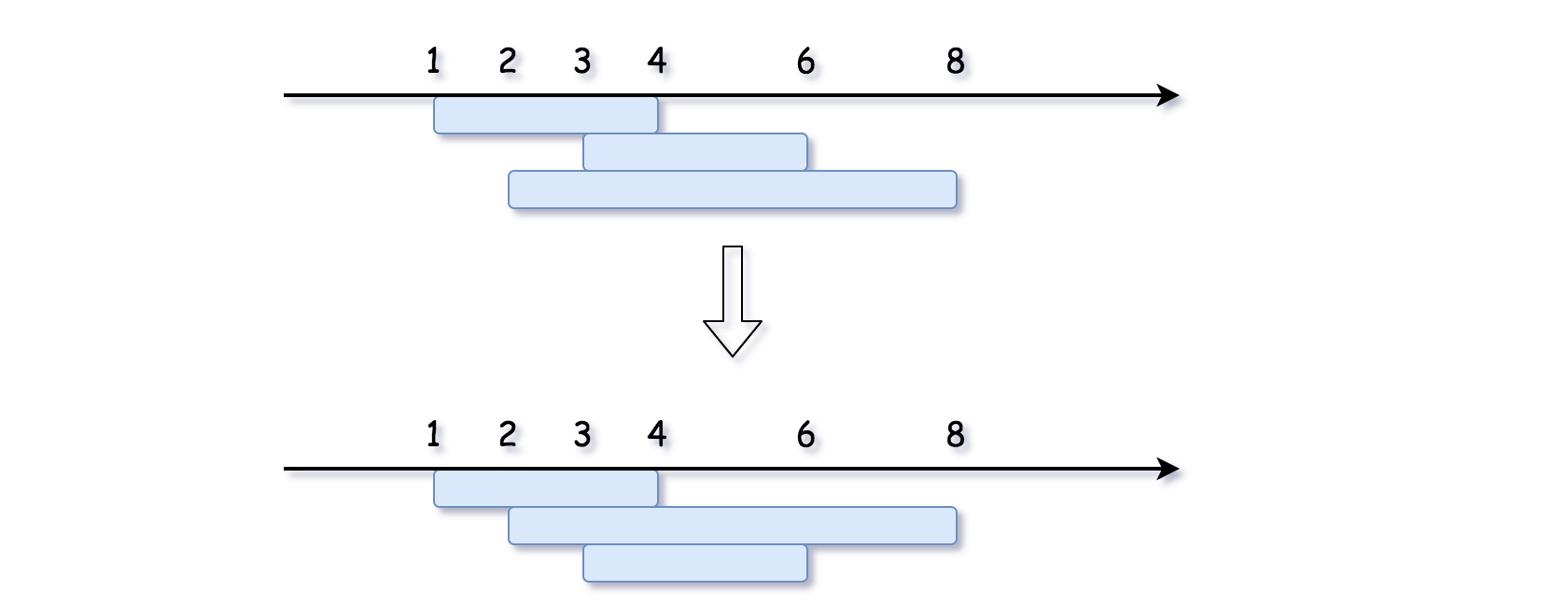
-
Let us consider two subsequent intervals after sorting. Since sorting ensures that start1 < start2, it’s sufficient to compare the end boundaries:
- If
end1 < end2, the intervals won’t completely cover one another, though they have some overlapping.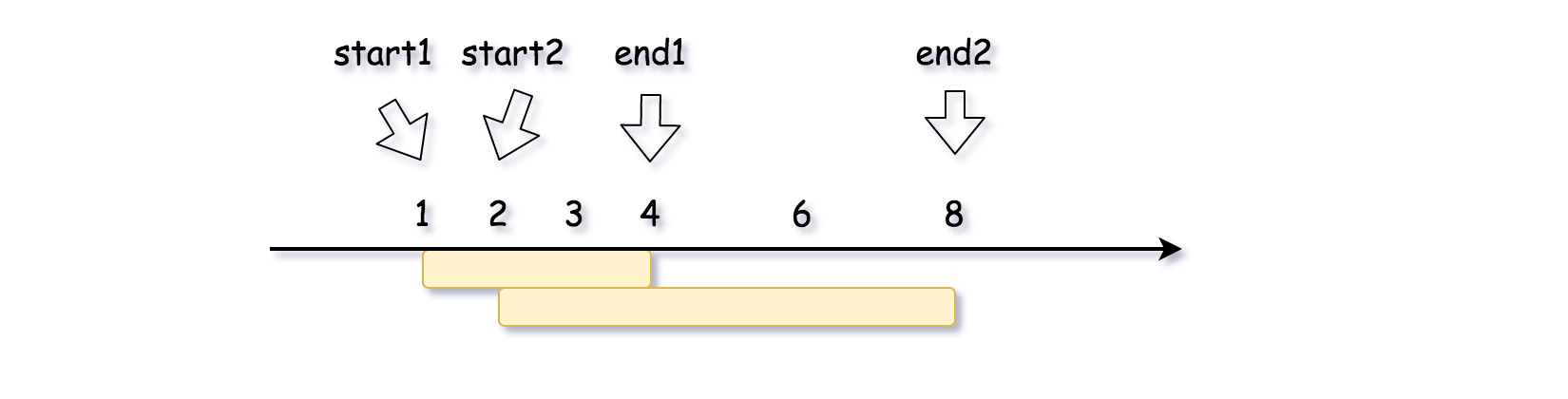
- If
end1 >= end2, the interval 2 is covered by the interval 1.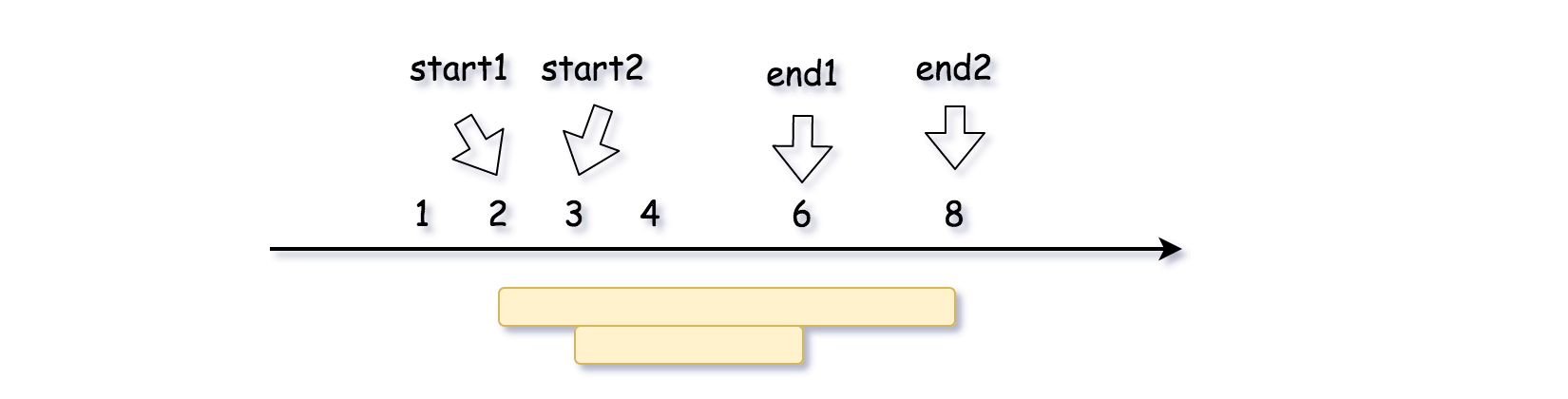
-
Edge case: How to treat intervals which share the same start point:
-
We’ve missed an important edge case in the previous discussion: what if two intervals share the start point, i.e. start1 == start2?
-
The above algorithm will fail because it cannot distinguish these two situations as follows:
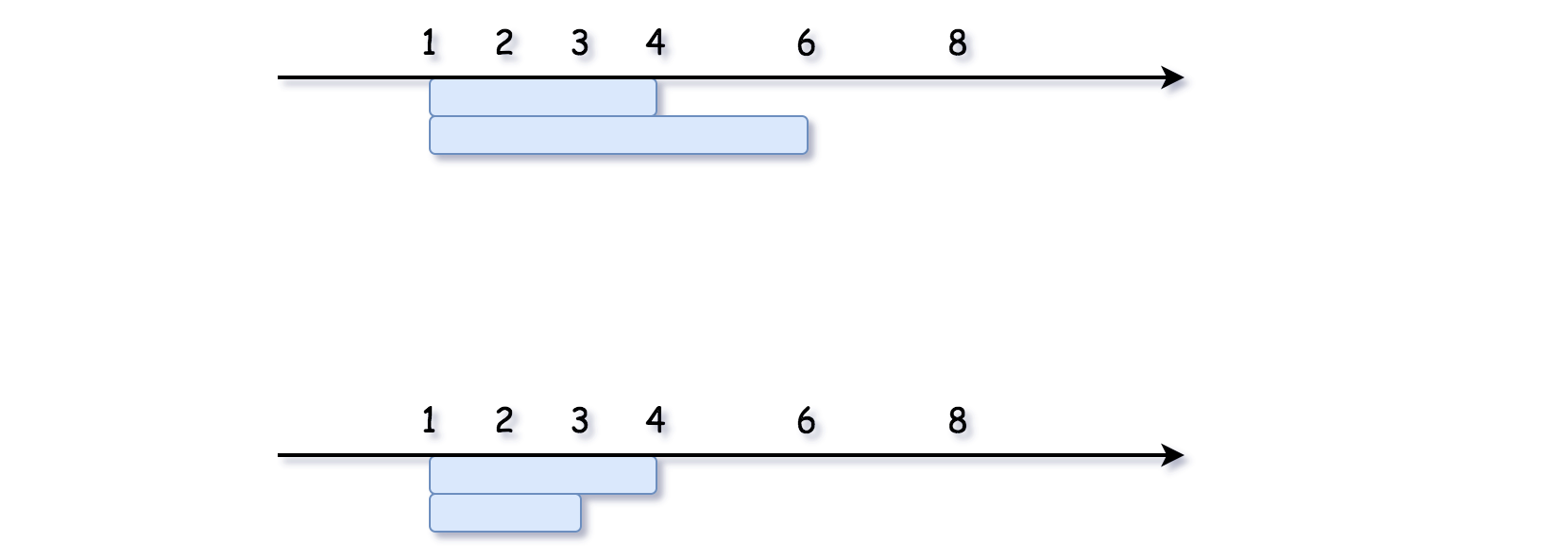
-
One of the intervals is covered by another, but if we sort only by the start point, we would not know which one. Hence, we need to sort by the end point as well.
If two intervals share the same start point, one has to put the longer interval in front.
- This way the above algorithm would work fine here as well. Moreover, it can deal with more complex cases, like the one below:
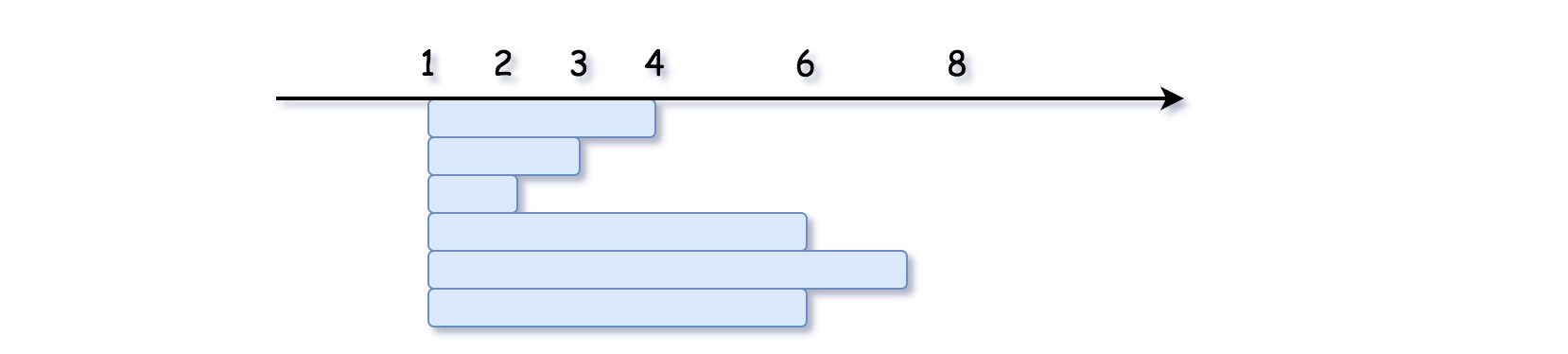
-
- If
- Algorithm:
- Sort in the ascending order by the start point. If two intervals share the same start point, put the longer one to be the first. If the array is sorted by start point in ascending order and end point in descending order, then we just need to check whether the current interval’s end is less or equal than previous end point. If it is, then the current interval is covered by one of previous intervals. Otherwise, the current interval’s starting point should be always greater or equal than the previous end point.
- Initiate the number of non-covered intervals:
count = 0. - Iterate over sorted intervals and compare end points.
- If the current interval is not covered by the previous one
end > prev_end, increase the number of non-covered intervals. Assign the current interval to be previous for the next step. - Otherwise, the current interval is covered by the previous one. Do nothing.
- If the current interval is not covered by the previous one
- Return
count. - For e.g.,
[1, 3], [2, 3], [2, 5], [2, 4]. Sorting the start point in ascending order and end point in descending order, we get,[1, 3], [2, 5], [2, 4], [2, 3].- For interval
[2, 5], since 5 is not <= 3, there is no overlap. - For interval
[2, 4], since 4 <= 5,[2, 4]is covered by one of the previous intervals. - For interval
[2, 3], since 3 <= 4,[2, 3]is covered by one of the previous intervals.
- For interval
class Solution:
def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:
if len(intervals) == 1:
return 1
# sort by start point in ascending order and end point in descending order
# in other words, sort by start point.
# If two intervals share the same start point
# put the longer one to be the first.
intervals.sort(key = lambda x: (x[0], -x[1]))
count = 0
prev_end = 0
for _, end in intervals:
# if current interval is not covered
# by the previous one
if end > prev_end:
count += 1
prev_end = end
return count
Complexity
- Time: \(O(n\log{n})\) since the sorting dominates the complexity of the algorithm.
- Space: \({O(n)}\) or \(\mathcal{O}(\log{n})\)
- The space complexity of the sorting algorithm depends on the implementation of each program language.
- For instance, the
sorted()function in Python is implemented with the Timsort algorithm whose space complexity is \(\mathcal{O}(n)\). - In Java, the Arrays.sort() is implemented as a variant of quicksort algorithm whose space complexity is \(\mathcal{O}(\log{n})\).
[1344/Medium] Angle Between Hands of a Clock
Problem
-
Given two numbers,
hourandminutes, return the smaller angle (in degrees) formed between the hour and the minute hand. -
Answers within
10^-5of the actual value will be accepted as correct. -
Example 1:
Input: hour = 12, minutes = 30
Output: 165
- Example 2:
Input: hour = 3, minutes = 30
Output: 75
- Example 3:
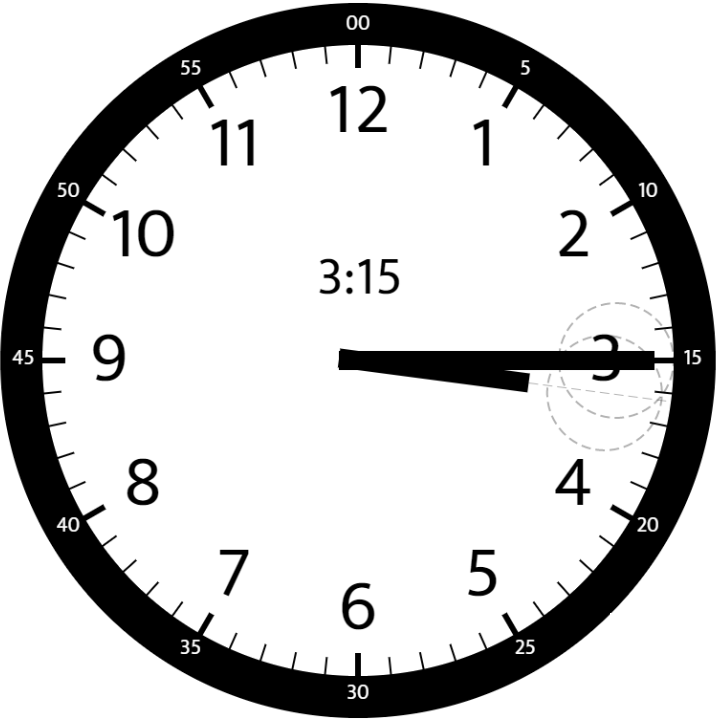
Input: hour = 3, minutes = 15
Output: 7.5
- Constraints:
1 <= hour <= 120 <= minutes <= 59
- See problem on LeetCode.
Solution: Mathematical Solution
- The minute hand moves by
minute_deg_per_min = 360° / 60 = 6°per minute. - The hour hand moves by
hour_deg_per_hour = 360° / 12 = 30°per hour. -
The hour hand has an additional movement of
hour_deg_per_min = hour_deg_per_hour / 60 = 30° / 60 = 0.5°per minute. - Therefore we get the following movements:
hour_hand_deg = (hour * hour_deg_per_hour) + (minutes * hour_deg_per_min) = hour * 30 + minutes * 0.5
minute_hand_deg = minutes * minute_deg_per_min = minutes * 6
- We need the absolute difference between those two:
diff_deg = |hour_hand_deg - minute_hand_deg| = |hour * 30 + minutes * 0.5 - minutes * 6| = |hour * 30 - minutes * 5.5|
- As we can easily see when looking at a clock there are two different angles between the hands:
- The minimum angle on one side is between 0° and 180°.
- The maximum angle on the other side is between 180° and 360°.
- We need the minimum angle. If our formula returned a number above 180° we got the maximum angle. We can calculate the minimum angle by subtracting the maximum angle from 360°.
class Solution:
def angleClock(self, hour: int, minutes: int) -> float:
diff = abs(30 * hour - 5.5 * minutes)
return diff if diff <= 180 else 360 - diff
Complexity
- Time: \(O(1)\)
- Space: \(O(1)\)
[1389/Easy] Create Target Array in the Given Order
Problem
-
Given two arrays of integers
numsandindex. Your task is to create target array under the following rules:- Initially target array is empty.
- From left to right read
nums[i]andindex[i], insert at indexindex[i]the valuenums[i]in target array. - Repeat the previous step until there are no elements to read in
numsandindex.
-
Return the target array.
-
It is guaranteed that the insertion operations will be valid.
-
Example 1:
Input: nums = [0,1,2,3,4], index = [0,1,2,2,1]
Output: [0,4,1,3,2]
Explanation:
nums index target
0 0 [0]
1 1 [0,1]
2 2 [0,1,2]
3 2 [0,1,3,2]
4 1 [0,4,1,3,2]
- Example 2:
Input: nums = [1,2,3,4,0], index = [0,1,2,3,0]
Output: [0,1,2,3,4]
Explanation:
nums index target
1 0 [1]
2 1 [1,2]
3 2 [1,2,3]
4 3 [1,2,3,4]
0 0 [0,1,2,3,4]
- Example 3:
Input: nums = [1], index = [0]
Output: [1]
- Constraints:
1 <= nums.length, index.length <= 100nums.length == index.length0 <= nums[i] <= 1000 <= index[i] <= i
- See problem on LeetCode.
Solution: Insert into list with .insert()
- The
.insert()method inserts an element to the list at the specified index. The syntax islist.insert(index, element).
class Solution:
def createTargetArray(self, n: List[int], i: List[int]) -> List[int]:
t = []
for num in range(len(n)):
t.insert(i[num], n[num])
return t
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Iterate using zip, insert into list with .insert()
class Solution:
def createTargetArray(self, nums: List[int], index: List[int]) -> List[int]:
res = []
for i, j in zip(nums, index):
res.insert(j, i)
return res
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[1446/Easy] Consecutive Characters
Problem
-
The power of the string is the maximum length of a non-empty substring that contains only one unique character.
-
Given a string
s, return the power ofs. -
Example 1:
Input: s = "leetcode"
Output: 2
Explanation: The substring "ee" is of length 2 with the character 'e' only.
- Example 2:
Input: s = "abbcccddddeeeeedcba"
Output: 5
Explanation: The substring "eeeee" is of length 5 with the character 'e' only.
- Constraints:
1 <= s.length <= 500s consists of only lowercase English letters.
- See problem on LeetCode.
Solution:
class Solution:
def maxPower(self, s: str) -> int:
ans = count = 1
for i in range(1, len(s)):
if s[i-1] == s[i]:
count += 1
ans = max(ans, count)
else:
count = 1
return ans
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[1480/Easy] Running Sum of 1D Array
Problem
-
Given an array
nums. We define a running sum of an array asrunningSum[i] = sum(nums[0]…nums[i]). -
Return the running sum of
nums. -
Example 1:
Input: nums = [1,2,3,4]
Output: [1,3,6,10]
Explanation: Running sum is obtained as follows: [1, 1+2, 1+2+3, 1+2+3+4].
- Example 2:
Input: nums = [1,1,1,1,1]
Output: [1,2,3,4,5]
Explanation: Running sum is obtained as follows: [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1].
- Example 3:
Input: nums = [3,1,2,10,1]
Output: [3,4,6,16,17]
- Constraints:
1 <= nums.length <= 1000-10^6 <= nums[i] <= 10^6
- See problem on LeetCode.
Solution: List slicing
- On each iteration of the for loop, we append the sum up to that index (sliced list) to a new list.
class Solution:
def runningSum(self, nums: List[int]) -> List[int]:
res = []
for i in range(len(nums)):
res.append(sum(nums[:i+1]))
return res
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: DP
class Solution:
def runningSum(self, nums: List[int]) -> List[int]:
dp = [0] * (len(nums)+1)
for index in range(1,len(nums)+1):
dp[index] = dp[index-1]+nums[index-1]
return dp[1:]
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: Add previous to current
def runningSum(self, nums: List[int]) -> List[int]:
n = len(nums)
for i in range(1, n):
nums[i] += nums[i-1]
return nums
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[1570/Medium] Dot Product of Two Sparse Vectors
Problem
-
Given two sparse vectors, compute their dot product.
- Implement class
SparseVector:SparseVector(nums)Initializes the object with the vectornumsdotProduct(vec)Compute the dot product between the instance of SparseVector andvec
-
A sparse vector is a vector that has mostly zero values, you should store the sparse vector efficiently and compute the dot product between two SparseVector.
-
Follow up: What if only one of the vectors is sparse?
- Example 1:
Input: nums1 = [1,0,0,2,3], nums2 = [0,3,0,4,0]
Output: 8
Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
v1.dotProduct(v2) = 1*0 + 0*3 + 0*0 + 2*4 + 3*0 = 8
- Example 2:
Input: nums1 = [0,1,0,0,0], nums2 = [0,0,0,0,2]
Output: 0
Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
v1.dotProduct(v2) = 0*0 + 1*0 + 0*0 + 0*0 + 0*2 = 0
- Example 3:
Input: nums1 = [0,1,0,0,2,0,0], nums2 = [1,0,0,0,3,0,4]
Output: 6
- Constraints:
n == nums1.length == nums2.length1 <= n <= 10^50 <= nums1[i], nums2[i] <= 100
- See problem on LeetCode.
Solution: Mark non-zero seen and multiply-add (MADD) them
class SparseVector:
def __init__(self, nums: List[int]):
self.seen = {}
for i, n in enumerate(nums):
if n:
self.seen[i] = n
# Return the dotProduct of two sparse vectors
def dotProduct(self, vec: 'SparseVector') -> int:
res = 0
for j, n in vec.seen.items():
if j in self.seen:
res += n * self.seen[j]
return res
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: One-liner
class SparseVector:
def __init__(self, A: List[int]):
self.m = {i: x for i, x in enumerate(A) if x}
def dotProduct(self, other: 'SparseVector') -> int:
return sum([x * y for i, x in self.m.items() for j, y in other.m.items() if i == j])
Complexity
- Time: \(O(n)\)
- Space: $$O(n)$
[1662/Easy] Check If Two String Arrays are Equivalent
Problem
-
Given two string arrays
word1andword2, return true if the two arrays represent the same string, and false otherwise. -
A string is represented by an array if the array elements concatenated in order forms the string.
-
Example 1:
Input: word1 = ["ab", "c"], word2 = ["a", "bc"]
Output: true
Explanation:
word1 represents string "ab" + "c" -> "abc"
word2 represents string "a" + "bc" -> "abc"
The strings are the same, so return true.
- Example 2:
Input: word1 = ["a", "cb"], word2 = ["ab", "c"]
Output: false
- Example 3:
Input: word1 = ["abc", "d", "defg"], word2 = ["abcddefg"]
Output: true
- Constraints:
1 <= word1.length, word2.length <= 1031 <= word1[i].length, word2[i].length <= 1031 <= sum(word1[i].length), sum(word2[i].length) <= 103word1[i] and word2[i] consist of lowercase letters.
- See problem on LeetCode.
Solution: Use ''.join()
class Solution:
def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:
return "".join(word1) == "".join(word2)
Complexity
- Time: \(O(max(n,m)\) where \(n\) and \(m\) are the lengths of
word1andword2respectively - Space: $$O(1)$
[1629/Easy] Slowest Key
-
A newly designed keypad was tested, where a tester pressed a sequence of
nkeys, one at a time. -
You are given a string
keysPressedof lengthn, wherekeysPressed[i]was thei-thkey pressed in the testing sequence, and a sorted listreleaseTimes, wherereleaseTimes[i]was the time thei-thkey was released. Both arrays are 0-indexed. The 0th key was pressed at the time 0, and every subsequent key was pressed at the exact time the previous key was released. -
The tester wants to know the key of the keypress that had the longest duration. The
i-thkeypress had a duration ofreleaseTimes[i] - releaseTimes[i - 1], and the 0th keypress had a duration ofreleaseTimes[0]. -
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key may not have had the same duration.
-
Return the key of the keypress that had the longest duration. If there are multiple such keypresses, return the lexicographically largest key of the keypresses.
-
Example 1:
Input: releaseTimes = [9,29,49,50], keysPressed = "cbcd"
Output: "c"
Explanation: The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
- Example 2:
Input: releaseTimes = [12,23,36,46,62], keysPressed = "spuda"
Output: "a"
Explanation: The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
- Constraints:
releaseTimes.length == n
keysPressed.length == n
2 <= n <= 1000
1 <= releaseTimes[i] <= 109
releaseTimes[i] < releaseTimes[i+1]
keysPressed contains only lowercase English letters.
- See problem on LeetCode.
Solution: Max-heap
from heapq import heappush
class Solution:
def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:
res, prev = (0, []), 0
for time, letter in zip(releaseTimes, keysPressed):
if time - prev > res[0]:
res = (time - prev, [-ord(letter)])
elif time - prev == res[0]:
heappush(res[1], -ord(letter))
prev = time
return chr(-res[1][0])
Solution: Calculate successive keys’ release times and compare with the max duration
- Using
max():
class Solution:
def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:
key = [keysPressed[0]]
max_dur = releaseTimes[0]
for i in range(1, len(releaseTimes)):
if releaseTimes[i] - releaseTimes[i - 1] == max_dur:
key.append(keysPressed[i])
if releaseTimes[i] - releaseTimes[i - 1] > max_dur:
max_dur = releaseTimes[i] - releaseTimes[i - 1]
key = [keysPressed[i]]
return max(key)
- Using
sorted():
class Solution:
def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:
res, prev = (0, []), 0
for time, letter in zip(releaseTimes, keysPressed):
if time - prev > res[0]:
res = (time - prev, [letter])
elif time - prev == res[0]:
res[1].append(letter)
prev = time
return sorted(res[1])[-1]
- Same approach; cleaner:
class Solution:
def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:
res, prev = (0, ''), 0
for time, letter in zip(releaseTimes, keysPressed):
if time - prev >= res[0]:
res = max(res, (time - prev, letter))
prev = time
return res[1]
Complexity
- Time: \(O(n)\)
- Space: $$O(1)$
[1641/Medium] Count Sorted Vowel Strings
Problem
- Given an integer
n, return the number of strings of lengthnthat consist only of vowels(a, e, i, o, u)and are lexicographically sorted. -
A string
sis lexicographically sorted if for all validi,s[i]is the same as or comes befores[i+1]in the alphabet. - Example 1:
Input: n = 1
Output: 5
Explanation: The 5 sorted strings that consist of vowels only are ["a","e","i","o","u"].
- Example 2:
Input: n = 2
Output: 15
Explanation: The 15 sorted strings that consist of vowels only are
["aa","ae","ai","ao","au","ee","ei","eo","eu","ii","io","iu","oo","ou","uu"].
Note that "ea" is not a valid string since 'e' comes after 'a' in the alphabet.
- Example 3:
Input: n = 33
Output: 66045
- Constraints:
1 <= n <= 50
- See problem on LeetCode.
Solution: Brute Force Using Backtracking
- Intuition:
- Backtracking is a general approach that works by identifying potential candidates and incrementally builds the solution using depth first search. Once the required goal is reached, we backtrack to explore another potential candidate.
- The backtracking solution for the given problem would be, to begin with, the first vowel character, continue using the same vowel until we build a string of length \(n\). Post that, backtrack and use the next character.
- As we are picking up each vowel character in alphabetically sorted order (first
a, thene, theni, and so on), we know that the resultant string is always lexicographically sorted. - Example, For
n = 3, pick the first vowela, continue picking up the same vowel until we reach \(n\). The resultant string would beaaa. Now that we have found our first combination, backtrack and pick up the next charactere. Our next string would beaae. The process continues until all the vowel characters are explored.
- Algorithm:
- As we start with the first vowel a then e and so on, we need a way to determine the current vowel in a recursive function. We use an integer variable vowel for that purpose, where 1 denotes a, 2 denotes e, and so on.
- We begin with \(n\) positions and first vowel
a(1)and use method countVowelStringUtil to recursively compute all the combinations. - On every recursion, we decrement n by 1 as we have used up that position and continue passing the same vowel. On the backtrack, we move on to the next vowel.
- Base Case:
- If
n = 0, we have reached the end of the string and found one combination. Hence, we return 1 and backtrack.
- If
- We try all the possibilities where adding the new vowel doesn’t break the lexicographic order. For example, if the last character of our actual possibility is ‘e’, we can’t add an ‘a’ after it.
def count(n, last=''):
if n == 0:
return 1
else:
nb = 0
for vowel in ['a', 'e', 'i', 'o', 'u']:
if last <= vowel:
nb += count(n-1, vowel)
return nb
Complexity
- Time: \(\mathcal{O}(n^{5})\). We have to calculate the size of the recursion tree. Let’s analyze the number of nodes generated at each level. The following figure illustrates the number of enumerations at level 2.
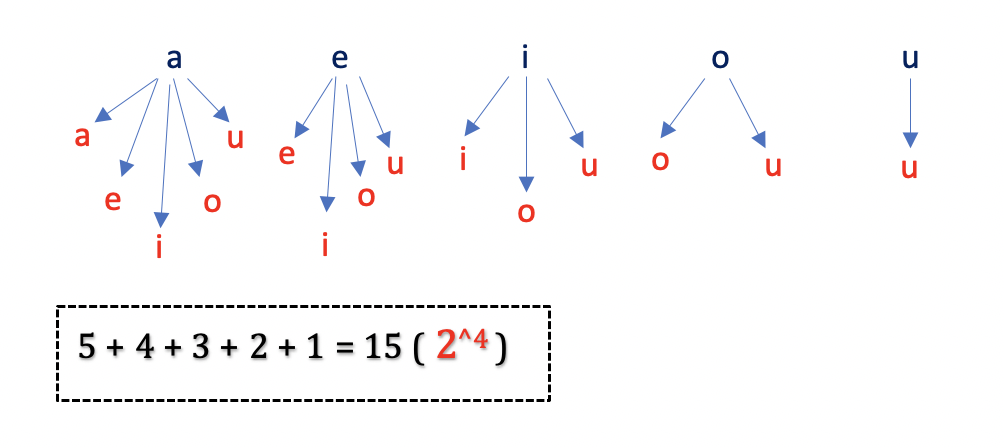
- Space: \(\mathcal{O}(n)\). This space will be used to store the recursion stack. We can’t have more than \(n\) recursive calls on the call stack at any time.
Solution: Recursion + Memoization, Top Down Dynamic Programming
- If you have solved problems on Dynamic Programming before, it is pretty easy to optimize the Approach 2 using Memoization. In the above approach, the problem can be broken down into subproblems. On drawing the recursion tree, it is evident that the same subproblems are computed multiple times.
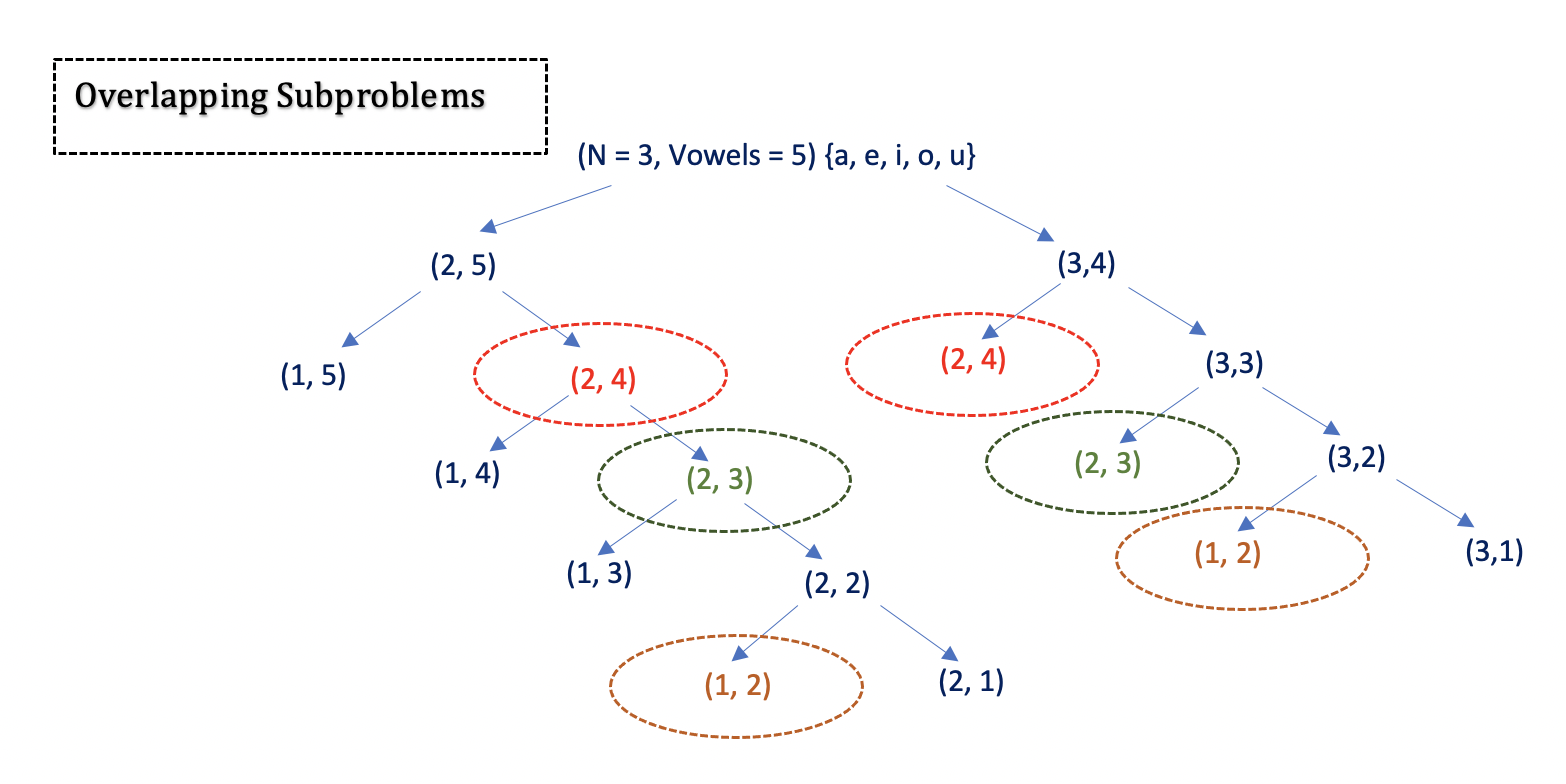
-
In the above recursion tree, we could see that subproblems
(2, 4),(2, 3)and(1, 2)are computed multiple times and the result would be always the same. The problem has Overlapping Subproblem and can be solved using Dynamic Programming. - Algorithm:
- We could have stored the results of our computation for the first time and used it later. This technique of computing once and returning the stored value is called Memoization.
- As we must store results for every \(n\) and \(\text{vowels}\), we use a two dimensional array \(\text{memo}\) of size
n x 5and follow the following steps for each recursive call:- Check in the memo if we have already calculated results for a given \(n\) and \(\text{vowels}\) and return the result stored in the memo.
- Save the results of any calculations to \(\text{memo}\).
Since arrays are 0-indexed, we initialize the array of size (n + 1, 5 + 1) and use the range 1..n and 1..5 for easier understanding and keeping it consistent with the previous approach.
- Key Insight:
- The fact that we are building strings from vowels really doesn’t matter. What does matter is that we have 5 elements and we want to know how many combinations (with replacement) we can make.
- Approach:
- Each iteration we have 2 choices. Add the current letter to the string or move on to the next letter.
- Once the string is n characters long, return 1 to signify we made 1 string. And if we reach the 6th letter, then return 0 because there are only 5 vowels to choose from so we cannot complete the string.
- Finally as the recursive function unwinds sum up how many strings were made.
@functools.lru_cache(None)
class Solution:
def countVowelStrings(self, n: int) -> int:
def helper(i, j):
if i == 5:
return 0
if j == 0:
return 1
return helper(i+1, j) + helper(i, j-1)
return helper(0, n)
Complexity
- Time: \(\mathcal{O}(n)\), as for every \(n\) and \(\text{vowels}\) we calculate result only once, the total number of nodes in the recursion tree would be
n x 5, which is roughly equal to \(n\). - Space: \(\mathcal{O}(n)\), as we use a 2D array \(\text{memo}\) of size
n x 5and the size of internal call stack would also be \(n\) (As explained in Approach 2), the space complexity would be \(\mathcal{O}(n+n) = \mathcal{O}(n)\).
Solution: One-liner
def countVowelStrings(self, n: int) -> int:
return len(list(itertools.combinations_with_replacement(range(5), n)))
Solution: Bottom Up Dynamic Programming, Tabulation
- Intuition:
- This is another approach to solve the Dynamic Programming problems. We use the iterative approach and store the result of subproblems in bottom-up fashion also known as Tabulation. We store the results of previous computations in tabular format and use those results for the next computations.
- Algorithm:
- We maintain a 2D array,
dpof sizen x 5where,dp[n][vowels]denotes the total number of combinations for givennand number of\text{vowels}. Using the recurrence relation established in Approach 2, we could iteratively calculate the value fordp[n][vowels]as,dp[n][vowels] = dp[n - 1][vowels] + dp[n][vowels - 1] - As this is the Bottom Up approach to solve the problem, we must initialize the table for the base cases. The base cases are the same as in Approach 2.
- If
n = 1, the number of combinations are always equal to number ofvowels. Hence, we initialize all the values ofdp[1][vowels]withvowels. - If
vowels = 1, the number of combinations are always equal to 1. Hence, we initialize all the values ofdp[n][1]with 1.
- If
- We maintain a 2D array,
class Solution:
def countVowelStrings(self, k: int) -> int:
dp = [1] * 5
for _ in range(1, k):
for i in range(1, 5):
dp[i] = dp[i] + dp[i-1]
return sum(dp)
Complexity
- Time: \(\mathcal{O}(n)\), as we iterate
5 x ntimes to fill thedparray, the time complexity is approximately \(\mathcal{O}(5 \cdot n) =\mathcal{O}(n)\). - Space: \(\mathcal{O}(n)\), as we use a 2D array of size
n x 5, the space complexity would be \(\mathcal{O}(n)\).
Solution: Math
- Intuition and Algorithm:
- The problem is a variant of finding Combinations. Mathematically, the problem can be described as, given 5 vowels (let k = 5k=5), we want to find the number of combinations using only nn vowels. Also, we can repeat each of those vowels multiple times.
In other words, from \(k\) vowels (\(k = 5\)), we can choose \(n\) vowels with repetition. Denoted as \(\left(\!\!{k \choose n}\!\!\right)\), the formulae for Combination with Repetition is given by \(\left(\!\!{k \choose n}\!\!\right) = \frac{(k + n - 1)!}{ (k - 1)! n!}\)
- We know that the \(k\) value is 5 as there are always 5 vowels to choose from. Substituting \(k\) as 5 in above formulae, \(\left(\!\!{5\choose n}\!\!\right) = \frac{(n+4) \cdot (n+3) \cdot (n+2) \cdot (n+1)}{24}\)
- The derivation can be illustrated as follows.

- The problem is a variant of finding Combinations. Mathematically, the problem can be described as, given 5 vowels (let k = 5k=5), we want to find the number of combinations using only nn vowels. Also, we can repeat each of those vowels multiple times.
class Solution:
def countVowelStrings(self, k: int) -> int:
return (k + 4) * (k + 3) * (k + 2) * (k + 1) // 24
Complexity
- Time: \(\mathcal{O}(1)\), as the approach runs in constant time.
- Space: \(\mathcal{O}(1)\), as the approach uses constant extra space.
[1678/Easy] Goal Parser Interpretation
Problem
-
You own a Goal Parser that can interpret a string command. The command consists of an alphabet of “G”, “()” and/or “(al)” in some order. The Goal Parser will interpret “G” as the string “G”, “()” as the string “o”, and “(al)” as the string “al”. The interpreted strings are then concatenated in the original order.
-
Given the string command, return the Goal Parser’s interpretation of command.
-
Example 1:
Input: command = "G()(al)"
Output: "Goal"
Explanation: The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal".
- Example 2:
Input: command = "G()()()()(al)"
Output: "Gooooal"
- Example 3:
Input: command = "(al)G(al)()()G"
Output: "alGalooG"
- Constraints:
1 <= command.length <= 100command consists of "G", "()", and/or "(al)" in some order.
- See problem on LeetCode.
Solution: Replace longest substring first, then replace smaller ones
class Solution:
def interpret(self, command: str) -> str:
command = command.replace('()','o')
command = command.replace('(', '')
command = command.replace(')','')
return command
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) since a new string is created when applying
.replace()(as strings are immutable)
[1732/Easy] Find the Highest Altitude
Problem
-
There is a biker going on a road trip. The road trip consists of
n + 1points at different altitudes. The biker starts his trip on point0with altitude equal0. -
You are given an integer array
gainof lengthnwheregain[i]is the net gain in altitude between pointsiandi + 1for all (0 <= i < n). Return the highest altitude of a point. -
Example 1:
Input: gain = [-5,1,5,0,-7]
Output: 1
Explanation: The altitudes are [0,-5,-4,1,1,-6]. The highest is 1.
- Example 2:
Input: gain = [-4,-3,-2,-1,4,3,2]
Output: 0
Explanation: The altitudes are [0,-4,-7,-9,-10,-6,-3,-1]. The highest is 0.
- Constraints:
n == gain.length1 <= n <= 100-100 <= gain[i] <= 100
- See problem on LeetCode.
Solution: DP
class Solution:
def largestAltitude(self, gain: List[int]) -> int:
dp = [0] * (len(gain)+1)
dp[0] = 0
for index in range (1, len(gain)+1):
dp[index] = dp[index-1] + gain[index-1]
return max(dp)
Solution: Use the gain list for iteration and append the sum of the i-th element of “res” and the i-th element of the “gain” list; then, find the max of the resulting list
class Solution:
def largestAltitude(self, gain: List[int]) -> int:
res = [0]
for i in range(len(gain)):
res.append(res[i] + gain[i])
return max(res)
[1762/Medium] Buildings With an Ocean View
Problem
- There are
nbuildings in a line. You are given an integer arrayheightsof sizenthat represents the heights of the buildings in the line. - The ocean is to the right of the buildings. A building has an ocean view if the building can see the ocean without obstructions. Formally, a building has an ocean view if all the buildings to its right have a smaller height.
-
Return a list of indices (0-indexed) of buildings that have an ocean view, sorted in increasing order.
- Example 1:
Input: heights = [4,2,3,1]
Output: [0,2,3]
Explanation: Building 1 (0-indexed) does not have an ocean view because building 2 is taller.
- Example 2:
Input: heights = [4,3,2,1]
Output: [0,1,2,3]
Explanation: All the buildings have an ocean view.
- Example 3:
Input: heights = [1,3,2,4]
Output: [3]
Explanation: Only building 3 has an ocean view.
- Constraints:
1 <= heights.length <= 1051 <= heights[i] <= 109
- See problem on LeetCode.
Solution: Reverse traversal and check for height violation
class Solution:
def findBuildings(self, heights: List[int]) -> List[int]:
retList = []
retList.append(len(heights)-1)
maxVal = heights[len(heights)-1]
for index in range(len(heights)-2,-1,-1):
if(heights[index] > maxVal):
maxVal = heights[index]
retList.append(index)
return reversed(retList) # sorted(retList)
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
[1650/Medium] Lowest Common Ancestor of a Binary Tree III
-
Given two nodes of a binary tree
pandq, return their lowest common ancestor (LCA). -
Each node will have a reference to its parent node. The definition for Node is below:
class Node {
public int val;
public Node left;
public Node right;
public Node parent;
}
-
According to the definition of LCA on Wikipedia: “The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself).”
-
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
- Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition.
- Example 3:
Input: root = [1,2], p = 1, q = 2
Output: 1
- Constraints:
The number of nodes in the tree is in the range [2, 105].-109 <= Node.val <= 109All Node.val are unique.p != qp and q exist in the tree.
- See problem on LeetCode.
Solution: Iteration
- The idea is to store the parents (
path) from root top, and then checkq’s path.
"""
# Definition for a Node.
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.parent = None
"""
class Solution:
def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
path = set()
while p:
path.add(p)
p = p.parent
while q not in path:
q = q.parent
return q
Solution: Find depth difference, move pointers to the same level, then move pointers up until they meet
- We first find the depth of each pointer, and then move each pointer to the same level in the tree. Then, we move the pointers up level by level until they meet.
- Summary:
- Find the depth of each pointer.
- Move the deeper pointer up until it is at the same level as the other pointer.
- Move each pointer up level-by-level until they meet
- Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 8 Output: 3
- Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5
"""
# Definition for a Node.
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.parent = None
"""
class Solution:
def get_depth(self, p):
# helper function to find the depth of the pointer in the tree
depth = 0
while p:
p = p.parent
depth += 1
return depth
def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
# find the depth of each pointer
p_depth = self.get_depth(p)
q_depth = self.get_depth(q)
# Move the lower pointer up so that they are each at the same level.
# For the smaller depth (p_depth < q_depth or q_depth < p_depth),
# the loop will be skipped and the pointer will stay at the same depth.
for _ in range(p_depth - q_depth):
p = p.parent
for _ in range(q_depth - p_depth):
q = q.parent
# Now that they are at the same depth, move them up the tree in parallel until they meet
while p != q:
p=p.parent
q=q.parent
return p
Complexity
- Time: \(O(h)\)
- Space: \(O(1)\)
Solution: Recursion + Set
class Solution(object):
def lowestCommonAncestor(self, p, q):
pVals = set()
def traverse_up(root):
if root == None or root in pVals:
return root
pVals.add(root)
return traverse_up(root.parent)
# This works because `None` in python evaluates to `False`, so doing `None or Node` will return `Node`.
return traverse_up(p) or traverse_up(q)
[1887/Medium] Reduction Operations to Make the Array Elements Equal
Problem
- Given an integer array
nums, your goal is to make all elements innumsequal. To complete one operation, follow these steps:- Find the largest value in
nums. Let its index bei(0-indexed) and its value be largest. If there are multiple elements with the largest value, pick the smallesti. - Find the next largest value in
numsstrictly smaller than largest. Let its value benextLargest. - Reduce
nums[i]tonextLargest.
- Find the largest value in
-
Return the number of operations to make all elements in
numsequal. - Example 1:
Input: nums = [5,1,3]
Output: 3
Explanation: It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums[0] to 3. nums = [3,1,3].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums[0] to 1. nums = [1,1,3].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums[2] to 1. nums = [1,1,1].
- Example 2:
Input: nums = [1,1,1]
Output: 0
Explanation: All elements in nums are already equal.
- Example 3:
Input: nums = [1,1,2,2,3]
Output: 4
Explanation: It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums[4] to 2. nums = [1,1,2,2,2].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums[2] to 1. nums = [1,1,1,2,2].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums[3] to 1. nums = [1,1,1,1,2].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums[4] to 1. nums = [1,1,1,1,1].
- Constraints:
1 <= nums.length <= 5 * 1041 <= nums[i] <= 5 * 104
- See problem on LeetCode.
Solution: Sort counter in descending order and build result by adding frequencies
- Algorithm:
- Go through numbers and their counts in decreasing order of frequencies.
- We keep track of remaining numbers we need to change in each iteration and add it to our result
res.
- Explanation:
sorted(Counter(nums).items(), reverse=True)gives items and their counts in reverse order- We are doing
items()instead of just taking values() as we want to order the elements in dictionary by the keys and not values.
- Example:
- Let’s take a look at
[1, 2, 2, 5, 5, 43]. - We look at 43 and add 1 to
to_change(as one of 43 needs to be changed to next number). - We look at 5 and add
to_changeto result (changing 43 to 5), and add two 5’s, which isnew_elementstoto_change. At this stage, we haveto_change = 3. - We do so until the end when we are at 1, and we end up adding remaining 2’s to the result. Note that we drop the last
new_elementsfor 1’s (since it doesn’t reflect inres).
- Let’s take a look at
class Solution:
def reductionOperations(self, nums: List[int]) -> int:
res = to_change = 0
for _, new_elements in sorted(Counter(nums).items(), reverse=True):
res += to_change
to_change += new_elements
return res
Complexity
- Time: \(O(n\log{n})\) owing to the sort
- Space: \(O(n)\) for storing the counts
Solution: Derive count add n-1-i
- First sort
nums, then go from left to right, if a mismatch is found at indexi, i.e.nums[i] != nums[i+1], then addn-1-ito the result.

class Solution:
def reductionOperations(self, nums: List[int]) -> int:
nums.sort()
n = len(nums)
count = 0
for i in range(n-1):
if nums[i] != nums[i+1]:
count += n-1-i
return count
Complexity
- Time: \(O(n\log{n})\) owing to the sort + \(O(n)\) owing to
numstraversal = \(O(n\log{n})\) - Space: \(O(1)\)
Solution: One-liner
- Same approach as above. First sort
nums, then go from left to right, if a mismatch is found at indexi, i.e.nums[i-1] != nums[i], then addn-ito the result.
class Solution:
def reductionOperations(self, nums: List[int]) -> int:
nums, n = sorted(nums), len(nums)
return sum([n-i if nums[i-1] != nums[i] else 0 for i in range(1, n)])
Complexity
- Time: \(O(n\log{n})\) owing to the sort + \(O(n)\) owing to
numstraversal = \(O(n\log{n})\) - Space: \(O(1)\)
[1911/Medium] Maximum Alternating Subsequence Sum
Problem
- The alternating sum of a 0-indexed array is defined as the sum of the elements at even indices minus the sum of the elements at odd indices.
- For example, the alternating sum of
[4,2,5,3]is(4 + 5) - (2 + 3) = 4. - Given an array nums, return the maximum alternating sum of any subsequence of nums (after reindexing the elements of the subsequence).
- A subsequence of an array is a new array generated from the original array by deleting some elements (possibly none) without changing the remaining elements’ relative order. For example, [2,7,4] is a subsequence of
[4,2,3,7,2,1,4](the underlined elements), while[2,4,2]is not. - Example 1:
Input: nums = [4,2,5,3]
Output: 7
Explanation: It is optimal to choose the subsequence [4,2,5] with alternating sum (4 + 5) - 2 = 7.
- Example 2:
Input: nums = [5,6,7,8]
Output: 8
Explanation: It is optimal to choose the subsequence [8] with alternating sum 8.
- Example 3:
Input: nums = [6,2,1,2,4,5]
Output: 10
Explanation: It is optimal to choose the subsequence [6,1,5] with alternating sum (6 + 5) - 1 = 10.
- Constraints:
1 <= nums.length <= 1051 <= nums[i] <= 105
- See problem on LeetCode.
Solution: Add and subtract current number from max count
def maxAlternatingSum(self, A):
odd = even = 0
for a in A:
odd, even = [max(odd, even - a), max(even, odd + a)]
return even
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[1920/Easy] Build Array from Permutation
Problem
-
Given a zero-based permutation
nums(0-indexed), build an arrayansof the same length whereans[i] = nums[nums[i]]for each0 <= i < nums.lengthand return it. -
A zero-based permutation nums is an array of distinct integers from
0 to nums.length - 1(inclusive). -
Example 1:
Input: nums = [0,2,1,5,3,4]
Output: [0,1,2,4,5,3]
Explanation: The array ans is built as follows:
ans = [nums[nums[0]], nums[nums[1]], nums[nums[2]], nums[nums[3]], nums[nums[4]], nums[nums[5]]]
= [nums[0], nums[2], nums[1], nums[5], nums[3], nums[4]]
= [0,1,2,4,5,3]
- Example 2:
Input: nums = [5,0,1,2,3,4]
Output: [4,5,0,1,2,3]
Explanation: The array ans is built as follows:
ans = [nums[nums[0]], nums[nums[1]], nums[nums[2]], nums[nums[3]], nums[nums[4]], nums[nums[5]]]
= [nums[5], nums[0], nums[1], nums[2], nums[3], nums[4]]
= [4,5,0,1,2,3]
- Constraints:
1 <= nums.length <= 10000 <= nums[i] < nums.lengthThe elements in nums are distinct.
-
Follow-up: Can you solve it without using an extra space (i.e.,
O(1)memory)? - See problem on LeetCode.
Solution: Simple list comprehension
class Solution:
def buildArray(self, nums: List[int]) -> List[int]:
return [nums[i] for i in nums]
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: Simple list comprehension
def buildArray(self, nums: List[int]) -> List[int]:
n = len(nums);
for i in range(n):
nums[i] += n*(nums[nums[i]]%n)
for i in range(n):
nums[i] = nums[i] // n
return nums
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[2042/Easy] Check if Numbers Are Ascending in a Sentence
Problem
- A sentence is a list of tokens separated by a single space with no leading or trailing spaces. Every token is either a positive number consisting of digits
0-9with no leading zeros, or a word consisting of lowercase English letters.- For example,
"a puppy has 2 eyes 4 legs"is a sentence with seven tokens:"2"and"4"are numbers and the other tokens such as"puppy"are words.
- For example,
- Given a string
srepresenting a sentence, you need to check if all the numbers insare strictly increasing from left to right (i.e., other than the last number, each number is strictly smaller than the number on its right in s). -
Return
Trueif so, orFalseotherwise. - Example 1:

Input: s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles"
Output: true
Explanation: The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
- Example 2:
Input: s = "hello world 5 x 5"
Output: false
Explanation: The numbers in s are: 5, 5. They are not strictly increasing.
- Example 3:
Input: s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s"
Output: false
Explanation: The numbers in s are: 7, 51, 50, 60. They are not strictly increasing.
- Constraints:
3 <= s.length <= 200s consists of lowercase English letters, spaces, and digits from 0 to 9, inclusive.The number of tokens in s is between 2 and 100, inclusive.The tokens in s are separated by a single space.There are at least two numbers in s.Each number in s is a positive number less than 100, with no leading zeros.s contains no leading or trailing spaces.
- See problem on LeetCode.
Solution: Split the string, find numbers, check if current number is greater than previous
class Solution:
def areNumbersAscending(self, s: str) -> bool:
words = s.split(" ")
prev = 0
for word in words:
if word.isnumeric(): # or word.isdigit()
# https://datagy.io/python-isdigit
if int(word) <= prev:
return False
prev = int(word)
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\) for
words
Solution: One-liner
class Solution:
def areNumbersAscending(self, s: str) -> bool:
num = [int(i) for i in s.split() if i.isnumeric()]
#check if in ascending order and unique
return True if num == sorted(num) and len(num)==len(set(num)) else False
Complexity
- Time: \(O(n\log{n})\) due to sorting
- Space: \(O(n)\)
Solution: Accumulate digits of every number, check if current number is greater than previous
class Solution:
def areNumbersAscending(self, s: str) -> bool:
prev = -1
curr = -1
temp = []
for ch in s:
if ch.isdigit(): # or ord(character) >= 48 and ord(character) <= 57:
# accumulate all the digits of the number
temp.append(ch)
# the below else is reached when we've accumulated all the digits number
else:
if len(temp) > 0:
curr = int("".join(temp))
if curr <= prev:
return False
else:
prev = curr
temp.clear() # or temp = []
# check the last number
if len(temp) > 0 and int("".join(temp)) <= prev:
return False
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[2060/Hard] Check if an Original String Exists Given Two Encoded Strings
Problem
-
An original string, consisting of lowercase English letters, can be encoded by the following steps:
- Arbitrarily split it into a sequence of some number of non-empty substrings.
- Arbitrarily choose some elements (possibly none) of the sequence, and replace each with its length (as a numeric string).
- Concatenate the sequence as the encoded string.
-
For example, one way to encode an original string “
abcdefghijklmnop” might be: - Split it as a sequence:
["ab", "cdefghijklmn", "o", "p"]. - Choose the second and third elements to be replaced by their lengths, respectively. The sequence becomes
["ab", "12", "1", "p"]. - Concatenate the elements of the sequence to get the encoded string: “ab121p”.
-
Given two encoded strings
s1ands2, consisting of lowercase English letters and digits 1-9 (inclusive), return true if there exists an original string that could be encoded as boths1ands2. Otherwise, return false. -
Note: The test cases are generated such that the number of consecutive digits in
s1ands2does not exceed 3. - Example 1:
Input: s1 = "internationalization", s2 = "i18n"
Output: true
Explanation: It is possible that "internationalization" was the original string.
- "internationalization"
-> Split: ["internationalization"]
-> Do not replace any element
-> Concatenate: "internationalization", which is s1.
- "internationalization"
-> Split: ["i", "nternationalizatio", "n"]
-> Replace: ["i", "18", "n"]
-> Concatenate: "i18n", which is s2
- Example 2:
Input: s1 = "l123e", s2 = "44"
Output: true
Explanation: It is possible that "leetcode" was the original string.
- "leetcode"
-> Split: ["l", "e", "et", "cod", "e"]
-> Replace: ["l", "1", "2", "3", "e"]
-> Concatenate: "l123e", which is s1.
- "leetcode"
-> Split: ["leet", "code"]
-> Replace: ["4", "4"]
-> Concatenate: "44", which is s2.
- Example 3:
Input: s1 = "a5b", s2 = "c5b"
Output: false
Explanation: It is impossible.
- The original string encoded as s1 must start with the letter 'a'.
- The original string encoded as s2 must start with the letter 'c'.
- Constraints:
1 <= s1.length, s2.length <= 40s1 and s2 consist of digits 1-9 (inclusive), and lowercase English letters only.The number of consecutive digits in s1 and s2 does not exceed 3.
- See problem on LeetCode.
Solution: Top-down DP
- Preliminaries:
- To get the ending index of the numeric substring of ‘s’ starting at ‘start’; we use the following code:-
def getValidPrefixLength(s,start): end = start while end < len(s) and s[end].isdigit(): end += 1 return end- To get all possibles lengths that the numeric substrings ‘s’ could represent we use the following code:-
@lru_cache(None) def possibleLengths(s): """Return all possible lengths represented by numeric string s.""" lengths = {int(s)} for i in range(1, len(s)): # add all lengths by splitting numeric string s at index i # & sum of first split part(i.e. x) and second split part(i.e. y) gives the answer lengths |= {x+y for x in possibleLengths(s[:i]) for y in possibleLengths(s[i:])} return length - Main logic:
- The main logic is implement a top-down dynamic programming based approach that takes in current pointers of both strings
s1ands2as well as the amount of prefix length lead thats2has overs1. We consider six cases in the DP in the following order:- both have reached end,
s1has not reached end ands1has numeric prefix,s2has not reached end ands2has numeric prefix,- There is no prefix lead difference between
s1ands2, s2leads overs1,s1leads overs2.
- The main logic is implement a top-down dynamic programming based approach that takes in current pointers of both strings
- Below is the self-explanatory commented code telling how these cases are implemented:
@lru_cache(None)
def dp(i, j, diff):
"""Return True if s1[i:] matches s2[j:] with given differences."""
# If both have reached end return true if none of them are leading
if i == len(s1) and j == len(s2): return diff == 0
# s1 has not reached end and s1 starts with a digit
if i < len(s1) and s1[i].isdigit():
i2 = getValidPrefixLength(s1,i)
for L in possibleLengths(s1[i:i2]):
# substract since lead of s2 decreases by L
if dp(i2, j, diff-L): return True
# s2 has not reached end and s2 starts with a digit
elif j < len(s2) and s2[j].isdigit():
j2 = getValidPrefixLength(s2,j)
for L in possibleLengths(s2[j:j2]):
# add since lead of s2 increases by L
if dp(i, j2, diff+L): return True
# if none of them have integer prefix or a lead over the other
elif diff == 0:
# if only one of them has reached end or current alphabets are not the same
if i == len(s1) or j == len(s2) or s1[i] != s2[j]: return False
# skip same alphabets
return dp(i+1, j+1, 0)
# if none of them have integer prefix & s2 lead over s1
elif diff > 0:
# no s1 to balance s2's lead
if i == len(s1): return False
# move s1 pointer forward and reduce diff
return dp(i+1, j, diff-1)
# if none of them have integer prefix & s1 lead over s2
else:
# no s2 to balance s1's lead
if j == len(s2): return False
# move s2 pointer forward and increase diff
return dp(i, j+1, diff+1)
- Finally, we call the function as
dp(0, 0, 0). The main code is:
from functools import lru_cache
class Solution:
def possiblyEquals(self, s1: str, s2: str) -> bool:
def getValidPrefixLength(s,start):
end = start
while end < len(s) and s[end].isdigit(): end += 1
return end
@lru_cache(None)
def possibleLengths(s):
"""Return all possible lengths represented by numeric string s."""
ans = {int(s)}
for i in range(1, len(s)):
# add all lengths by splitting numeric string s at i
ans |= {x+y for x in possibleLengths(s[:i]) for y in possibleLengths(s[i:])}
return ans
@lru_cache(None)
def dp(i, j, diff):
"""Return True if s1[i:] matches s2[j:] with given differences."""
# If both have reached end return true if none of them are leading
if i == len(s1) and j == len(s2): return diff == 0
# s1 has not reached end and s1 starts with a digit
if i < len(s1) and s1[i].isdigit():
i2 = getValidPrefixLength(s1,i)
for L in possibleLengths(s1[i:i2]):
# subtract since lead of s2 decreases by L
if dp(i2, j, diff-L): return True
# s2 has not reached end and s2 starts with a digit
elif j < len(s2) and s2[j].isdigit():
j2 = getValidPrefixLength(s2,j)
for L in possibleLengths(s2[j:j2]):
# add since lead of s2 increase by L
if dp(i, j2, diff+L): return True
# if none of them have integer prefix or a lead over the other
elif diff == 0:
# if only one of them has reached end or current alphabets are not the same
if i == len(s1) or j == len(s2) or s1[i] != s2[j]: return False
# skip same alphabets
return dp(i+1, j+1, 0)
# if none of them have integer prefix and s2 lead over s1
elif diff > 0:
# no s1 to balance s2's lead
if i == len(s1): return False
# move s1 pointer forward and reduce diff
return dp(i+1, j, diff-1)
# if none of them have integer prefix and s1 lead over s2
else:
# no s2 to balance s1's lead
if j == len(s2): return False
# move s2 pointer forward and increase diff
return dp(i, j+1, diff+1)
# start with starts of both s1 and s2 with no lead by any of them
return dp(0, 0, 0)
[2108/Easy] Find First Palindromic String in the Array
Problem
-
Given an array of strings
words, return the first palindromic string in the array. If there is no such string, return an empty string"". -
A string is palindromic if it reads the same forward and backward.
-
Example 1:
Input: words = ["abc","car","ada","racecar","cool"]
Output: "ada"
Explanation: The first string that is palindromic is "ada".
Note that "racecar" is also palindromic, but it is not the first.
Example 2:
Input: words = ["notapalindrome","racecar"]
Output: "racecar"
Explanation: The first and only string that is palindromic is "racecar".
- Example 3:
Input: words = ["def","ghi"]
Output: ""
Explanation: There are no palindromic strings, so the empty string is returned.
- Constraints:
1 <= words.length <= 1001 <= words[i].length <= 100words[i] consists only of lowercase English letters.
- See problem on LeetCode.
Solution
class Solution:
def firstPalindrome(self, words: List[str]) -> str:
for word in words:
if self.isPalindrome(word):
return word
return ""
def isPalindrome(self, word) -> bool:
l, r = 0, len(word)-1
while l < r:
if word[l] != word[r]:
return False
l += 1
r -= 1
return True
# or return word == word[::-1] (less efficient)
Complexity
- Time: \(O(nm)\) where \(n\) are the number of words in the input and \(m\) is the average length of each word.
- Space: \(O(n)\) for
word[::-1]