Distilled • LeetCode • Heap
- Pattern: Heap
- [23/Hard] Merge k Sorted Lists
- [347/Medium] Top K Frequent Elements
- [378/Medium] Kth Smallest Element in a Sorted Matrix
- [630/Hard] Course Schedule III
- [632/Hard] Smallest Range Covering Elements from K Lists
- [973/Medium] K Closest Points to Origin
- [1509/Medium] Minimum Difference Between Largest and Smallest Value in Three Moves
Pattern: Heap
[23/Hard] Merge k Sorted Lists
Problem
-
You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.
-
Merge all the linked-lists into one sorted linked-list and return it.
-
Example 1:
Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
1->4->5,
1->3->4,
2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6
- Example 2:
Input: lists = []
Output: []
Example 3:
Input: lists = [[]]
Output: []
- Constraints:
k == lists.length0 <= k <= 1040 <= lists[i].length <= 500-104 <= lists[i][j] <= 104lists[i] is sorted in ascending order.The sum of lists[i].length will not exceed 104.
- See problem on LeetCode.
Solution: Min-heap
-
A brute force solution could be to add all elements of the given ‘K’ lists to one list and sort it. If there are a total of ‘N’ elements in all the input lists, then the brute force solution will have a time complexity of \(O(N*\log{N})\) as we will need to sort the merged list. Can we do better than this? How can we utilize the fact that the input lists are individually sorted?
-
If we have to find the smallest element of all the input lists, we have to compare only the smallest (i.e. the first) element of all the lists. Once we have the smallest element, we can put it in the merged list. Following a similar pattern, we can then find the next smallest element of all the lists to add it to the merged list.
-
The best data structure that comes to mind to find the smallest number among a set of ‘K’ numbers is a Heap. Let’s see how can we use a heap to find a better algorithm.
- We can insert the first element of each array in a Min Heap.
- After this, we can take out the smallest (top) element from the heap and add it to the merged list.
- After removing the smallest element from the heap, we can insert the next element of the same list into the heap.
- We can repeat steps 2 and 3 to populate the merged list in sorted order.
-
Let’s take the Example-1 mentioned above to go through each step of our algorithm:
-
Given lists:
L1=[2, 6, 8], L2=[3, 6, 7], L3=[1, 3, 4]
- After inserting the first number from each list in the heap, the heap will have the following elements:

- We’ll take the top number from the heap, insert it into the merged list and add the next number in the heap.

- Again, we’ll take the top element of the heap, insert it into the merged list and add the next number to the heap.

- Repeating the above step, take the top element of the heap, insert it into the merged list and add the next number to the heap. As there are two 3s in the heap, we can pick anyone but we need to take the next element from the corresponding list to insert in the heap.

- We’ll repeat the above step to populate our merged array.
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
ListNode.__lt__ = lambda self, other: self.val < other.val
h = []
head = tail = ListNode(0)
for i in lists:
if i:
heapq.heappush(h, (i.val, i))
while h:
node = heapq.heappop(h)[1]
tail.next = node
tail = tail.next
if node.next:
heapq.heappush(h, (node.next.val, node.next))
return head.next
Complexity
- Time: Since we’ll be going through all the elements of all arrays and will be removing/adding one element to the heap in each step, the time complexity of the above algorithm will be \(O(N*logK)\), where \(N\) is the total number of elements in all the \(K\) input arrays.
- Space: The space complexity will be \(O(K)\) because, at any time, our min-heap will be storing one number from all the \(K\) input arrays.
[347/Medium] Top K Frequent Elements
Problem
-
Given an integer array
numsand an integerk, return thekmost frequent elements. You may return the answer in any order. -
Example 1:
Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]
- Example 2:
Input: nums = [1], k = 1
Output: [1]
- Constraints:
1 <= nums.length <= 105k is in the range [1, the number of unique elements in the array].It is guaranteed that the answer is unique.
- See problem on LeetCode.
Solution: Reverse sort counter output by frequency values
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
c = Counter(nums)
return sorted(c, key=lambda x: c[x], reverse=True)[:k]
- Same approach; much verbose:
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
frq = defaultdict(list)
for key, cnt in Counter(nums).items():
frq[cnt].append(key)
res = []
for times in reversed(range(len(nums) + 1)):
res.extend(frq[times])
if len(res) >= k: return res[:k]
return res[:k]
Complexity
- Time: \(O(n)\)
- Space: \(O(n)\)
Solution: Max-heap of size \(k\)
- Build a frequency dictionary - invert the sign of the frequency (negative frequency serves as the priority key for the heap later).
- Push all
(negative frequency, item)pairs into the heap. - Pop \(k\) items from heap and append to a result list.
- Return list.
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
if not nums:
return []
if len(nums) == 1:
return [nums[0]]
# first find freq - freq dict
d = {}
for num in nums:
if num in d:
d[num] -= 1 # reverse the sign on the freq for the heap's sake
else:
d[num] = -1
h = []
from heapq import heappush, heappop
for key in d:
heappush(h, (d[key], key)) # push (freq, item): O(log(k))
res = []
count = 0
while count < k:
freq, item = heappop(h) # O(log(k))
res.append(item)
count += 1
return res
Complexity
- Time: \(O(n\log{n})\)
- Space: \(O(n)\)
Solution: Min-heap of size \(n\)
- Build a frequency dictionary (freq is positive).
- Build a heap.
- Make sure heap contains \(k\) items at maximum by popping out the items with least frequency as you push to heap.
- The time complexity of adding an element in a heap is \(O(\log{k})\) and we do it \(n\) times that means \(O(n\log{k})\) time complexity for this step.
- Heap now contains \(k\) items (the desired output basically).
- Pop and append to the output list - \(O(k\log{k})\).
- Return list.
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
if len(nums) == 1:
return [nums[0]]
# freq dict
d = {}
for num in nums:
if num in d:
d[num] += 1
else:
d[num] = 1
# go over the n input items and
# insert k items into heap: O(n log(k))
h = []
from heapq import heappush, heappop
for key in d: # O(n)
heappush(h, (d[key], key)) # push (freq, item): O(log(k))
if len(h) > k:
heappop(h)
res = []
while h: # O(k)
freq, item = heappop(h) # O(log(k))
res.append(item)
return res
Complexity
- Time: \(O(n\log{k})\)
- Space: \(O(n)\)
[378/Medium] Kth Smallest Element in a Sorted Matrix
-
Given an
n x nmatrixwhere each of the rows and columns is sorted in ascending order, return thek-thsmallest element in the matrix. -
Note that it is the
k-thsmallest element in the sorted order, not thek-thdistinct element. -
You must find a solution with a memory complexity better than
O(n^2). -
Example 1:
Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: The elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8th smallest number is 13
Example 2:
Input: matrix = [[-5]], k = 1
Output: -5
- Constraints:
n == matrix.length == matrix[i].length1 <= n <= 300-109 <= matrix[i][j] <= 109All the rows and columns of matrix are guaranteed to be sorted in non-decreasing order.1 <= k <= n2
- See problem on LeetCode.
Solution: Sort
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
res = []
for r in matrix:
res += r
return sorted(res)[k-1]
Complexity
- Time: \(O(n\log{n})\)
- Space: \(O(1)\)
Solution: Binary search
-
Since each row and column of the matrix is sorted, is it possible to use Binary Search to find the Kth smallest number?
-
The biggest problem to use Binary Search, in this case, is that we don’t have a straightforward sorted array, instead, we have a matrix. As we remember, in Binary Search, we calculate the middle index of the search space (‘1’ to ‘N’) and see if our required number is pointed out by the middle index; if not we either search in the lower half or the upper half. In a sorted matrix, we can’t really find a middle. Even if we do consider some index as middle, it is not straightforward to find the search space containing numbers bigger or smaller than the number pointed out by the middle index.
- An alternative could be to apply the Binary Search on the “number range” instead of the “index range”. As we know that the smallest number of our matrix is at the top left corner and the biggest number is at the bottom right corner. These two numbers can represent the “range” i.e., the
startand theendfor the Binary Search. Here is how our algorithm will work:- Start the Binary Search with
start = matrix[0][0]andend = matrix[n-1][n-1]. - Find middle of the
startand theend. Thismiddlenumber is NOT necessarily an element in the matrix. - Count all the numbers smaller than or equal to middle in the matrix. As the matrix is sorted, we can do this in \(O(N)\).
- While counting, we can keep track of the “smallest number greater than
middle” (let’s call itn1) and at the same time the “biggest number less than or equal to the middle” (let’s call itn2). These two numbers will be used to adjust the “number range” for the Binary Search in the next iteration. - If the count is equal to ‘K’,
n2will be our required number as it is the “biggest number less than or equal to the middle”, and is definitely present in the matrix. - If the count is less than ‘K’, we can update
start = n2to search in the higher part of the matrix and if the count is greater than ‘K’, we can updateend = n1to search in the lower part of the matrix in the next iteration.
- Start the Binary Search with
- Here is a visual representation of the algorithm:



class Solution(object):
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
def count_less_equal(matrix, smaller, mid, larger):
count, n = 0, len(matrix)
row, col = n - 1, 0
while row >= 0 and col < n:
if matrix[row][col] > mid:
# as matrix[row][col] is bigger than the mid, let's keep track of the
# smallest number greater than the mid
larger = min(larger, matrix[row][col])
row -= 1
else:
# as matrix[row][col] is less than or equal to the mid, let's keep track of the
# biggest number less than or equal to the mid
smaller = max(smaller, matrix[row][col])
count += row + 1
col += 1
return count, smaller, larger
l, r = matrix[0][0], matrix[-1][-1]
while l < r:
mid = (l + r) // 2 # or l + (r - l) // 2
# calculate how many numbers are on the left of middle number
count, smaller, larger = count_less_equal(matrix, mid, l, r)
# or order = sum(bisect.bisect(row, m) for row in matrix) < k:
if count >= k:
r = smaller # search lower
else:
l = larger # search higher
return l
- Note that
bisect.bisect(array, x)returns an insertion point which comes after (to the right of) any existing entries ofxin array.
Complexity
- Time: The Binary Search could take \(O(\log{max-min})\) iterations where \(max\) is the largest and \(min\) is the smallest element in the matrix and in each iteration we take \(O(n)\) for counting, therefore, the overall time complexity of the algorithm will be \(O(n*\log{max-min})\)
- Space: \(O(1)\)
Solution: Binary search (cleaner)
- Same approach; cleaner:
class Solution(object):
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
def findCount(matrix, val):
count = 0
for row in matrix:
for col in row:
if col <= val: count += 1
return count
l, r = matrix[0][0], matrix[-1][-1]
while l < r:
mid = (l + r) // 2 # or l + (r - l) // 2
# calculate how many numbers are on the left of middle number
count = findCount(matrix, mid)
# or count = sum(bisect.bisect(row, m) for row in matrix) < k:
if count >= k:
r = mid # search lower
else:
l = mid + 1 # search higher
return l
Complexity
- Time: \(O(n\log{(max-min)})\) for the solution using
findCount()or \(O(\log{n}\log{(max-min)})\) for the solution usingbisect.bisect()wherenis number of rows.- \(O(n)\) for
findCount()or \(O(\log{n})\) forbisect.bisect() - \(O(\log{(max-min)})\) for the
whileloop
- \(O(n)\) for
- Space: \(O(1)\)
Solution: Min-Heap of size \(n\)
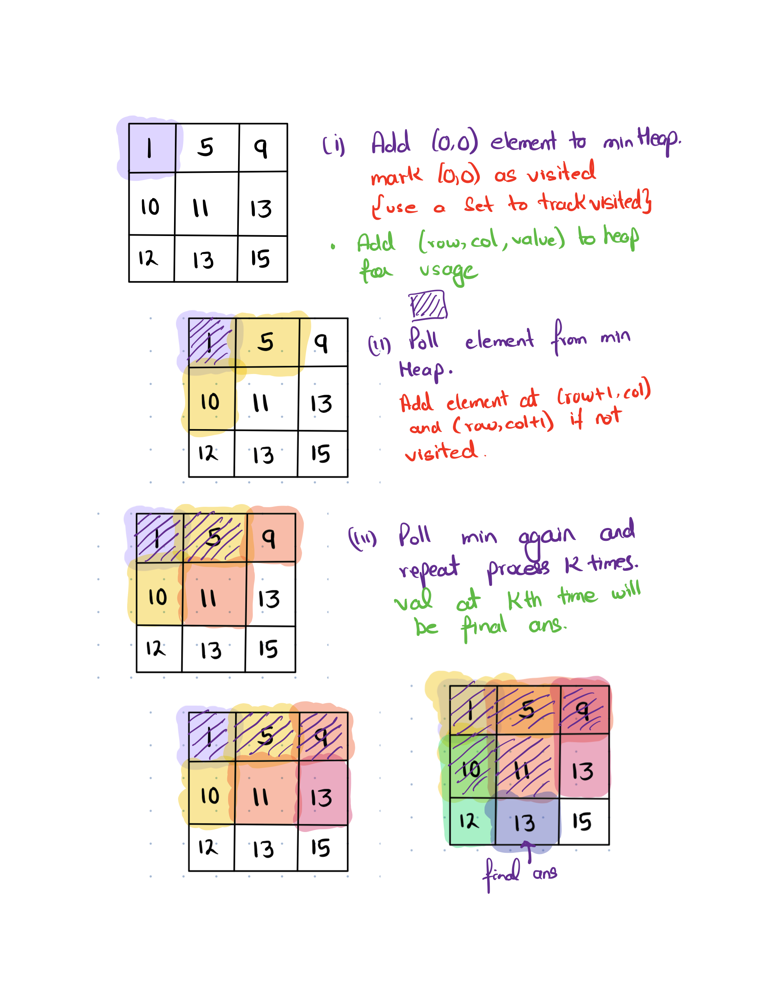
from heapq import heappush, heappop
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
a, res = [], -1
for r in matrix:
for e in r:
heappush(a, e)
for _ in range(k):
res = heappop(a)
return res
Complexity
- Time: \(n\) times
heappushis \(O(n\log{n})\) and \((k)\) timesheappopis \(O((k)\log{n})\). Overall, \(O((n+k)\log{n})\) - Space: \(O(1)\)
Solution: Min-Heap of size \(n\) with heapify
class Solution(object):
def kthSmallest(self, matrix, k):
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
import heapq
vals = [val for row in matrix for val in row]
heapq.heapify(vals)
for _ in range(k):
ans = heapq.heappop(vals)
return ans
Complexity
- Time: heapify is \(O(n)\) and \(k\) times pop is \(O(k \log{n})\) so overall time complexity is: \(O(n + k\log{n})\)
- Space: \(O(1)\)
Solution: Min-Heap of size \(k\)
- Same approach; better time complexity:
import heapq
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
if not matrix or not matrix[0]:
return -1
heap = []
for row in range(len(matrix)):
for col in range(len(matrix[0])):
# Negate element to emulate a max-heap
nextVal = -matrix[row][col]
# If the length of your heap is less than k, push elements
if len(heap) < k:
heapq.heappush(heap, nextVal)
# If your heap has k elements and if the current element is
# greater than the max element so far, pop out the current max
# and add the new one in
elif nextVal > heap[0]:
heapq.heappushpop(heap, nextVal)
return -heap[0]
Complexity
- Time: \(k\) times
heappushis \(O(k\log{n})\) and \((n-k)\) timesheappushpopis \(O((n - k)\log{n})\). Overall, \(O(n\log{n})\) - Space: \(O(1)\)
[630/Hard] Course Schedule III
-
There are
ndifferent online courses numbered from 1 to n. You are given an array courses wherecourses[i] = [durationi, lastDayi]indicate that theithcourse should be taken continuously fordurationidays and must be finished before or onlastDayi. -
You will start on the 1st day and you cannot take two or more courses simultaneously.
-
Return the maximum number of courses that you can take.
-
Example 1:
Input: courses = [[100,200],[200,1300],[1000,1250],[2000,3200]]
Output: 3
Explanation:
There are totally 4 courses, but you can take 3 courses at most:
First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day.
Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day.
Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day.
The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
- Example 2:
Input: courses = [[1,2]]
Output: 1
- Example 3:
Input: courses = [[3,2],[4,3]]
Output: 0
- Constraints:
1 <= courses.length <= 1041 <= durationi, lastDayi <= 104
- See problem on LeetCode.
Solution: Max heap acting as a priority-queue
- Idea:
-
If we think of this problem in a larger sense, we can envision a slightly more simplistic situation without the issues of the last day cutoff for each course. In that scenario, we could quite easily add up all the course durations, then selectively remove the courses with the longest remaining duration until we’ve found the ideal number of courses that will fit into our desired timeframe.
-
The trouble here, of course, is that we do have cutoffs for each course, which means we can no longer fill the entire time before removing courses. Instead, we’ll have to selectively backtrack and remove courses as we iterate through the input array (
C). -
As is often the case in a scheduling-type problem, this leads to a particular issue: we’ll want to sort the data in two distinctly different ways. Since we’ll be progressing through C as if we’re progressing through time, we’ll want to sort
Cbased on the courses’ cutoffs (end), but when we backtrack to potentially remove a course, we’ll want to sort the courses we’ve accepted by their duration (dur). -
The need for a data structure that will maintain its sort through insertions and max value removals means that we’re looking for a max priority queue or max-heap.
-
Once we’ve sorted
Cand set up our max priority queue or heap (pq/heap), it’s simply a matter of iterating throughC, adding the courses to pq/heap, and then removing the max duration course as necessary to stay underneath the currentendvalue with our accumulated duration (total). -
In order to minimize unnecessary insertions/removals, we can perform a few basic conditional checks to tell if they’re necessary. If the current course will already fit, we can just add it, or if the current course is a better fit than our longest course, then we can swap them.
-
Then, once we reach the end of
C, pq/heap should contain all the non-discarded courses, so we can return its size as our answer.
-
- Implementation:
- Note that to avoid having to use a custom comparator for Python, which defaults to a min heap, we can just switch the sign before insertion and after extraction to mimic a max heap.
from heapq import heappush
class Solution:
def scheduleCourse(self, C: List[List[int]]) -> int:
heap, total = [], 0
for dur, end in sorted(C, key=lambda el: el[1]):
if dur + total <= end:
total += dur
heappush(heap, -dur)
elif heap and -heap[0] > dur:
total += dur + heappop(heap)
heappush(heap, -dur)
return len(heap)
Complexity
-
Time: \(O\big(n \log n\big)\) where \(n\) is the length of \(C\), due to both the sort and the priority queue / heap implementation. At most \(n\) elements are added to the priority queue / heap implementation. Adding each element is followed by heapification, which takes \(O\big(\log n\big)\) time.
-
Space: \(O(n)\). The priority queue / heap data containing the durations of the courses taken can have at most \(n\) elements.
[632/Hard] Smallest Range Covering Elements from K Lists
Problem
-
You have
klists of sorted integers in non-decreasing order. Find the smallest range that includes at least one number from each of theklists. -
We define the range
[a, b]is smaller than range[c, d]ifb - a < d - cora < c if b - a==d - c. -
Example 1:
Input: nums = [[4,10,15,24,26],[0,9,12,20],[5,18,22,30]]
Output: [20,24]
Explanation:
List 1: [4, 10, 15, 24,26], 24 is in range [20,24].
List 2: [0, 9, 12, 20], 20 is in range [20,24].
List 3: [5, 18, 22, 30], 22 is in range [20,24].
- Example 2:
Input: nums = [[1,2,3],[1,2,3],[1,2,3]]
Output: [1,1]
- Constraints:
nums.length == k1 <= k <= 35001 <= nums[i].length <= 50-105 <= nums[i][j] <= 105nums[i] is sorted in non-decreasing order.
- See problem on LeetCode.
Solution
import heapq
class Solution:
def smallestRange(self, nums: List[List[int]]) -> List[int]:
result = []
hq = []
high = -sys.maxsize
for i in range(len(nums)):
heapq.heappush(hq, (nums[i][0], i, 0))
high = max(high, nums[i][0])
result = [hq[0][0], high]
while True:
num , listIndex, numIndex = heapq.heappop(hq)
if numIndex == len(nums[listIndex]) - 1:
break;
nextNum = nums[listIndex][numIndex + 1]
heapq.heappush(hq, (nextNum, listIndex, numIndex + 1))
high = max(high, nextNum)
if high - hq[0][0] < result[1] - result[0]:
result = [hq[0][0], high]
return result
Complexity
- Time: \(O(n\log{k})\)
- Space: \(O(k)\)
[973/Medium] K Closest Points to Origin
Problem
- Given an array of
pointswherepoints[i] = [x_, y_i]represents a point on the X-Y plane and an integerk, return thekclosest points to the origin(0, 0). - The distance between two points on the X-Y plane is the Euclidean distance (i.e.,
sqrt((x1 - x2)^2 + (y1 - y2)^2). - You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).
- Example 1:
Input: points = [[1,3],[-2,2]], k = 1
Output: [[-2,2]]
Explanation:
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest k = 1 points from the origin, so the answer is just [[-2,2]].
- Example 2:
Input: points = [[3,3],[5,-1],[-2,4]], k = 2
Output: [[3,3],[-2,4]]
Explanation: The answer [[-2,4],[3,3]] would also be accepted.
- Constraints:
1 <= k <= points.length <= 104-104 < x_i, y_i < 104
- See problem on LeetCode.
Solution: Sort
- Sort the list according to the distance to origin. However, note that this does more than the question has asked – we sorted all the input points, while the question only ask for top \(K\). To improve time complexity, we need to think about how to get we ask without extra effort. This is where the heap data structure comes in.
class Solution:
def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
points.sort(key = lambda P: P[0]**2+P[1]**2)
return points[:K]
Complexity
- Time: \(O(N \log{N})\)
Solution: Min-heap of size \(N\)
- We insert \(N\) distance measurements corresponding to each input point to a min-heap of size \(N\).
- Calling
heapq.heappop(distance)will pop the smallest item in the heap. So callingheappop()\(K\) times will be yield the result.
import heapq
class Solution:
def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
distance = []
for i in points:
heapq.heappush(distance, (i[0]**2 + i[1]**2, i))
K_points = []
for i in range(K):
K_points.append(heapq.heappop(distance)[1])
return K_points
- The problem with the above approach is that we stored all the \(N\) elements so the time complexity is \(O(N\log{N})\). Since we only need the top \(k\) smallest elements, we don’t care about the order of other elements.
- So if we keep a min-heap of size \(k\), use the
heap[0]element as threshold, iterate through the array, only the \(K\) elements will be added to the heap.
Complexity
- Time: Inserting an item to a heap of size \(n\) would take \(O(\log{n})\) time. And we do this for each of the \(n\) items/points. So runtime is \(O(n * \log{n})\) where \(n\) is the number of input points.
- Space: \(O(n)\) for our heap.
Solution: Min-heap of size \(K\)
- We store \(K\) distance measurements corresponding to each input point to a min-heap of size \(K\).
- If inserting an item makes the heap size larger than \(K\), then we immediately pop an item after inserting (
heappushpop()).
import heapq
class Solution:
def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
heap = []
for (x, y) in points:
dist = -(x*x + y*y)
if len(heap) == K:
heapq.heappushpop(heap, (dist, x, y))
else:
heapq.heappush(heap, (dist, x, y))
return [(x,y) for (dist, x, y) in heap]
Complexity
- Time: Inserting an item to a heap of size \(K\) would take \(O(\log{K})\) time. And we do this for each of the \(n\) items/points. So runtime is \(O(n * \log{K})\) where \(n\) is the number of input points.
- Space: \(O(K)\) for our heap.
Solution: Max heap of size \(K\)
- Since Python doesn’t have a built-in max heap, we use a min-heap to achieve maximum heap’s by storing inverted (negated) versions of the input points.
import heapq
class Solution:
def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
distance = []
for p in points:
if len(distance) <= K-1:
heapq.heappush(distance, (-p[0]**2-p[1]**2, p))
else:
if -p[0]**2-p[1]**2 > distance[0][0]:
heapq.heappop(distance)
heapq.heappush(distance, (-p[0]**2-p[1]**2, p)) # or heapq.heapreplace(distance, (-p[0]**2-p[1]**2, p))
res = []
for i in range(K):
res.append(heapq.heappop(distance)[1])
return res
Complexity
- Time:
heapqis a binary heap, with \(O(\log{n})\) push and \(O(\log{n})\) pop. \(n\) is the size of the minimum heap. In this case, \(n = K\). So the runtime is \(O(N * \log{K})\) where \(N\) is the length of points. - Space: \(O(K)\) for our heap.
Solution: Max heap of size \(N\) (Simpler)
import heapq
class Solution:
def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
heap = []
for x, y in points:
d = -(x*x + y*y)
heapq.heappush(heap, (d, x, y))
if len(heap) > K:
heapq.heappop(heap)
return [[x, y] for _, x, y in heap]
Complexity
- Time:
heapqis a binary heap, with \(O(\log{n})\) push and \(O(\log{n})\) pop. \(n\) is the size of the minimum heap. In this case, \(n = K\). So the runtime is \(O(N * \log{K})\) where \(N\) is the length of points. - Space: \(O(K)\) for our heap.
[1509/Medium] Minimum Difference Between Largest and Smallest Value in Three Moves
Problem
-
You are given an integer array nums. In one move, you can choose one element of nums and change it by any value.
-
Return the minimum difference between the largest and smallest value of nums after performing at most three moves.
-
Example 1:
Input: nums = [5,3,2,4]
Output: 0
Explanation: Change the array [5,3,2,4] to [2,2,2,2].
The difference between the maximum and minimum is 2-2 = 0.
- Example 2:
Input: nums = [1,5,0,10,14]
Output: 1
Explanation: Change the array [1,5,0,10,14] to [1,1,0,1,1].
The difference between the maximum and minimum is 1-0 = 1.
- Constraints:
1 <= nums.length <= 105-109 <= nums[i] <= 109
- See problem on LeetCode.
Solution: Sort, then look for the minimum difference among the first three and last three elements
- Intuition:
- If we can do 0 move, return
max(A) - min(A). - If we can do 1 move, return
min(the second max(A) - min(A), the max(A) - second min(A))since we’re looking to minimize the difference between the maximum and minimum element by either reducing the maximum element to the match the minimum element or increasing the minimum element to match the maximum element. and so on.
- If we can do 0 move, return
- Explanation:
- If there are 4 or less elements in it, we’re going to be left with 1 element at most, making the difference b/w min and max 0.
- If there are more elements, then we have one of these four choices:
- Get rid of the 3 biggest elements.
- Get rid of 2 biggest elements, and the smallest.
- Get rid of the biggest element, and 2 smallest.
- Get rid of the 3 smallest elements.
- And in these four choices respectively, the min and the max will be the following:
- 1st element, and 4th from the last.
- 2nd element, and 3rd from the last.
- 3rd element, and 2nd from the last.
- 4th element, and (1st from) the last.
- In other words, we simply need to take the pairwise difference b/w the 4 smallest elements in the array, and the 4 largest elements in the array (in reverse order). Sorting the entire array for this is inefficient. A more efficient way is provided by the
heapqmodule. - And of course, we can use this for any number of moves, not just 3. At a large number of moves though, it would be faster to sort the entire array.
-
Example:
A = [1,5,6,13,14,15,16,17] (note that the array is sorted) n = 8 Case 1: kill 3 biggest elements All three biggest elements can be replaced with 14 [1,5,6,13,14,15,16,17] -> [1,5,6,13,14,14,14,14] == can be written as A[n-4] - A[0] == (14-1 = 13) Case 2: kill 2 biggest elements + 1 smallest elements [1,5,6,13,14,15,16,17] -> [5,5,6,13,14,15,15,15] == can be written as A[n-3] - A[1] == (15-5 = 10) Case 3: kill 1 biggest elements + 2 smallest elements [1,5,6,13,14,15,16,17] -> [6,6,6,13,14,15,16,16] == can be written as A[n-2] - A[2] == (16-6 = 10) Case 4: kill 3 smallest elements [1,5,6,13,14,15,16,17] -> [13,13,13,13,14,15,16,17] == can be written as A[n-1] - A[3] == (17-13 = 4) Answer is the minimum of all these cases!
class Solution:
def minDifference(self, nums: List[int]) -> int:
nums.sort()
return 0 if len(nums) <= 4 else min(b - a for a, b in zip(nums[:4], nums[-4:]))
Complexity
- Time: \(O(n\log{n})\)
- Space: \(O(log{n})\)
Solution: Partial Sorting using a Heap, then look for the minimum difference among the first three and last three elements
class Solution:
def minDifference(self, nums: List[int]) -> int:
# return 0 if len(nums) <= 4 else min(a - b for a, b in zip(heapq.nlargest(4, nums), reversed(heapq.nsmallest(4, nums))))
return 0 if len(nums) <= 4 else min(a - b for a, b in zip(heapq.nlargest(4, nums), heapq.nsmallest(4, nums)[::-1]))
Complexity
- Time: \(O(n\log{k})\)
- Space: \(O(log{k})\)