Aman's AI Journal • Distilled • LeetCode • Dictionary/Hash Table/Set

Pattern: Dictionary/Hash Table/Set

Pattern: Dictionary/Hash Table/Set

[12/Medium] Integer to Roman

Problem

Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.

Symbol       Value
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

For example, 2 is written as II in Roman numeral, just two one’s added together. 12 is written as XII, which is simply X + II. The number 27 is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:
- I can be placed before V (5) and X (10) to make 4 and 9.
- X can be placed before L (50) and C (100) to make 40 and 90.
- C can be placed before D (500) and M (1000) to make 400 and 900.
Given an integer, convert it to a roman numeral.
Example 1:

Input: num = 3
Output: "III"
Explanation: 3 is represented as 3 ones.

Example 2:

Input: num = 58
Output: "LVIII"
Explanation: L = 50, V = 5, III = 3.

Example 3:

Input: num = 1994
Output: "MCMXCIV"
Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.

Constraints:
- 1 <= num <= 3999
See problem on LeetCode.

Solution: Dictionary

Just like Roman to Integer, this problem is most easily solved using a lookup table for the conversion between digit and numeral. In this case, we can easily deal with the values in descending order and insert the appropriate numeral (or numerals) as many times as we can while reducing the our target number (num) by the same amount.
Once num runs out, we can return ans.

class Solution:
    def intToRoman(self, num: int) -> str:
        val = [1000,900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1]
        rom = ["M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"]

        ans = ""
        for i in range(len(val)):
            while num >= val[i]:
                ans += rom[i]
                num -= val[i]
                
        return ans

Complexity

Time: $O(n)$
Space: $O(1)$ for val and rom

[13/Easy] Roman to Integer

Problem

Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.

Symbol       Value
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

For example, 2 is written as II in Roman numeral, just two one’s added together. 12 is written as XII, which is simply X + II. The number 27 is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:
- I can be placed before V (5) and X (10) to make 4 and 9.
- X can be placed before L (50) and C (100) to make 40 and 90.
- C can be placed before D (500) and M (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
Example 1:

Input: s = "III"
Output: 3
Explanation: III = 3.

Example 2:

Input: s = "LVIII"
Output: 58
Explanation: L = 50, V= 5, III = 3.

Example 3:

Input: s = "MCMXCIV"
Output: 1994
Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.

Constraints:
- 1 <= s.length <= 15
- s contains only the characters ('I', 'V', 'X', 'L', 'C', 'D', 'M').
- It is guaranteed that s is a valid roman numeral in the range [1, 3999].
See problem on LeetCode.

Solution: Reverse the numeral, check if previous symbol is >= than the current one

def romanToInt(self, s: str) -> int:
    res, prev = 0, 0
    mappingTable = {'I': 1, 'V': , 'X': 10, 'L': 50, 'C': 100, 'D': 500, 'M': 1000}
    
    for i in s[::-1]: # rev the s
        if mappingTable[i] >= prev:
            res += mappingTable[i] # sum the value iff previous value same or more
        else:
            res -= mappingTable[i] # subtract when value is like "IV" --> 5-1, "IX" --> 10 -1 etc 
        prev = mappingTable[i]
        
    return res

Complexity

Time: $O(n)$
Space: $O(1)$ for mappingTable

[146/Medium] LRU Cache

Problem

Design a data structure that follows the constraints of a Least Recently Used (LRU) cache.
Implement the LRUCache class:
- LRUCache(int capacity) Initialize the LRU cache with positive size capacity.
- int get(int key) Return the value of the key if the key exists, otherwise return -1.
- void put(int key, int value) Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.
The functions get and put must each run in O(1) average time complexity.
Example 1:

Input
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
Output
[null, null, null, 1, null, -1, null, -1, 3, 4]

Explanation
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1);    // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2);    // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1);    // return -1 (not found)
lRUCache.get(3);    // return 3
lRUCache.get(4);    // return 4

Constraints:
- 1 <= capacity <= 3000
- 0 <= key <= 104
- 0 <= value <= 105
- At most 2 * 105 calls will be made to get and put.
See problem on LeetCode.

Solution: Deque

The slow approach implementation is simple but it is not efficient.
Things to keep in mind:
- Putting:
  - Whenever you are putting a key-value pair in, you have to check whether the key already exists.
  - If it exists, you get that key-value pair, update the value and put that pair at the the end of the cache.
  - If the key does not exist, you check whether the cache size is already at limit.
    - If the cache size is at limit, pop the key-value pair at the beginning of the cache and push the new key-value pair at the end of the cache.
    - If the cache is still under size limit, simply push the new key-value pair at the end of the cache.
- Getting:
  - Whenever you are getting the value of the key, check whether the key exists in the cache.
    - If it exists, put that key-value pair at the end of the cache and return the value.
    - If it does not exist, return -1.

from collections import deque

class LRUCache:

    def __init__(self, capacity: int):
        self.size = capacity
        self.deque = deque()
    
    def _find(self, key: int) -> int:
        """ Linearly scans the deque for a specified key. Returns -1 if it does not exist, returns the index of the deque if it exists"""
        for i in range(len(self.deque)):
            n = self.deque[i]
            if n[0] == key:
                return i 
        return -1
    
    def get(self, key: int) -> int:
        idx = self._find(key)
        if idx == -1:
            return -1
        else:
            k, v = self.deque[idx]
            del self.deque[idx] # We have to put this pair at the end of the queue so, we have to delete it first
            self.deque.append((k, v)) # And now, we put it at the end of the queue. So, the most viewed ones will be always at the end and be saved from popping when new capacity got hit.
            return v
                
    def put(self, key: int, value: int) -> None:
        idx = self._find(key)
        if idx == -1:
            if len(self.deque) >= self.size:
                self.deque.popleft()
            self.deque.append((key,value))
        else:
            del self.deque[idx]
            self.deque.append((key, value))

Solution: Deque + Dictionary

class LRUCache:
    def __init__(self, capacity: int):
        self.cap = capacity
        self.dq = collections.deque()
        self.valueMap = {}

    def get(self, key: int) -> int:
        if key not in self.valueMap:
            return -1
        self.dq.remove(key)
        self.dq.append(key)
        
        return self.valueMap[key]

    def put(self, key: int, value: int) -> None:
        if key not in self.valueMap:
            if len(self.dq) == self.cap:
                del self.valueMap[self.dq.popleft()]
        else:
            self.dq.remove(key)
        
        self.dq.append(key)
        self.valueMap[key] = value

Note that you can also use plain dictionaries in place of a deque since they preserve the order of insertion. To update the order of the entry retrieved using get, you simply delete and insert it again.

Solution: `OrderedDict`

The fast approach implementation is much better using OrderedDict (so that you have $O(1)$ access time).
OrderedDict has .move_to_end() and .popitem(last=False) (set last=True if you want to pop the last element, last=False if you want to pop the first element) which make things easy.

from collections import OrderedDict

class LRUCache:

    def __init__(self, capacity: int):
        self.size = capacity
        self.cache = OrderedDict()
    
    def get(self, key: int) -> int:
        if key not in self.cache:
            return -1
        else:
            self.cache.move_to_end(key) # Refresh key as the newest one, move to end of OrderedDict
            # Can also use "v = self.dic.pop(key); self.dic[key] = v" in place of move_to_end(key) on older Python releases   
            return self.cache[key]

    def put(self, key: int, value: int) -> None:
        if key not in self.cache:
            if len(self.cache) >= self.size:
                self.cache.popitem(last=False) # last=True, LIFO; last=False, FIFO. We want to remove in FIFO fashion. 
        else:
            self.cache.move_to_end(key) # Gotta keep this pair fresh, move to end of OrderedDict
            
        self.cache[key] = value    

Complexity

Time: $O(1)$ access time
Space: $O(n)$

[208/Medium] Implement Trie (Prefix Tree)

Problem

A trie (pronounced as “try”) or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
- Trie() Initializes the trie object.
- void insert(String word) Inserts the string word into the trie.
- boolean search(String word) Returns true if the string word is in the trie (i.e., was inserted before), and false otherwise.
- boolean startsWith(String prefix) Returns true if there is a previously inserted string word that has the prefix prefix, and false otherwise.
Example 1:

Input
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
Output
[null, null, true, false, true, null, true]

Explanation
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // return True
trie.search("app");     // return False
trie.startsWith("app"); // return True
trie.insert("app");
trie.search("app");     // return True

Constraints:
- 1 <= word.length, prefix.length <= 2000
- word and prefix consist only of lowercase English letters.
- At most 3 * 104 calls in total will be made to insert, search, and startsWith.
See problem on LeetCode.

Solution: Dictionary without a `TrieNode` class

There is no need to create a TrieNode class. Using a dictionary can give much better performance. Nodes are replaced by dictionary. is_word is replaced by adding a - key to the dictionary.

class Trie(object):
    def __init__(self):
        self.trie = {}

    def insert(self, word):
        t = self.trie
        
        for c in word:
            if c not in t: t[c] = {}
            t = t[c]
            
        t["-"] = True

    def search(self, word):
        t = self.trie
        
        for c in word:
            if c not in t: return False
            t = t[c]
            
        return "-" in t

    def startsWith(self, prefix):
        t = self.trie
        
        for c in prefix:
            if c not in t: return False
            t = t[c]
            
        return True   

Complexity

Time: $O(n)$
Space: $O(n)$ for self.trie

Solution: Using a `TrieNode` class implemented using a dict/`defaultdict`

Using a dictionary to implement a TrieNode class:

class TrieNode:
    def __init__(self):
        self.childNodes = {}
        self.isWordEnd = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word: str) -> None:
        """
        we will start with root node and check for the first character
        if there is already a node present for the character we will fetch that node, else we will create a new node
        then we will iterate to next character
        """
        currNode = self.root
        for ch in word:
            node = currNode.childNodes.get(ch, TrieNode())
            currNode.childNodes[ch] = node
            currNode = node

        # after all the characters are traversed, mark the last node as end of word
        currNode.isWordEnd = True

    def search(self, word: str) -> bool:
        """
        we will start from root node and check for all the characters
        if we could not find a node for a character we will return False there
        once we iterate through all character we will check if that is a word end
        """

        currNode = self.root
        for ch in word:
            node = currNode.childNodes.get(ch) # or if ch not in currNode.childNodes:
            if not node:                       #        return False
                return False
            currNode = node

        return currNode.isWordEnd

    def startsWith(self, prefix: str) -> bool:
        """
        starts with is similar to search except here we don't have to check whether the last character is end of word
        """
        currNode = self.root
        for ch in prefix:
            node = currNode.childNodes.get(ch)
            if not node:
                return False
            currNode = node

        return True

Using a defaultdict to implement a TrieNode class:

from collections import defaultdict

class TrieNode(object):
    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.nodes = defaultdict(TrieNode) # Easy to insert new node.
        self.isword = False  # True for the end of the trie.

class Trie(object):
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word):
        """
        Inserts a word into the trie by creating nodes with individual chars.
        :type word: str
        :rtype: void
        """
        curr = self.root
        for char in word:
            curr = curr.nodes[char]
        curr.isword = True

    def search(self, word):
        """
        Returns True if the word is in the trie.
        :type word: str
        :rtype: bool
        """
        curr = self.root
        for char in word:
            if char not in curr.nodes:
                return False
            curr = curr.nodes[char]
        return curr.isword

    def startsWith(self, prefix):
        """
        Returns if there is any word in the trie
        that starts with the given prefix.
        :type prefix: str
        :rtype: bool
        """
        curr = self.root
        for char in prefix:
            if char not in curr.nodes:
                return False
            curr = curr.nodes[char]
        return True

Complexity

Time: $O(n)$
Space: $O(n)$ for self.nodes

[246/Medium] Strobogrammatic Number

Problem

Given a string num which represents an integer, return true if num is a strobogrammatic number.
A strobogrammatic number is a number that looks the same when rotated 180 degrees (looked at upside down).
Example 1:

Input: num = "69"
Output: true

Example 2:

Input: num = "88"
Output: true

Example 3:

Input: num = "962"
Output: false

Constraints:
- 1 <= num.length <= 50
- num consists of only digits.
- num does not contain any leading zeros except for zero itself.
See problem on LeetCode.

Solution: Set

def isStrobogrammatic(self, num):
    """
    :type num: str
    :rtype: bool
    """
    # note that maps is a set
    maps = {("0", "0"), ("1", "1"), ("6", "9"), ("8", "8"), ("9", "6")}
    i,j = 0, len(num) - 1
    
    while i <= j:
        if (num[i], num[j]) not in maps:
            return False
        i += 1
        j -= 1
    
    return True    

Complexity

Time: $O(n)$
Space: $O(1)$

[249/Medium] Group Shifted Strings

Problem

We can shift a string by shifting each of its letters to its successive letter.
- For example, "abc" can be shifted to be "bcd".
We can keep shifting the string to form a sequence.
- For example, we can keep shifting "abc" to form the sequence: "abc" -> "bcd" -> ... -> "xyz".
- Given an array of strings strings, group all strings[i] that belong to the same shifting sequence. You may return the answer in any order.
Example 1:

Input: strings = ["abc","bcd","acef","xyz","az","ba","a","z"]
Output: [["acef"],["a","z"],["abc","bcd","xyz"],["az","ba"]]

Example 2:

Input: strings = ["a"]
Output: [["a"]]

Constraints:
- 1 <= strings.length <= 200
- 1 <= strings[i].length <= 50
- strings[i] consists of lowercase English letters.
See problem on LeetCode.

Solution: Dictionary

We can solve this problem by mapping each string in strings to a key in a dictionary. We then return hashmap.values().

{
     (1, 1): ['abc', 'bcd', 'xyz'],  
  (2, 2, 1): ['acef'],   
      (25,): ['az', 'ba'],   
         (): ['a', 'z']
}

The key can be represented as a tuple of the “differences” between adjacent characters. Characters map to integers (e.g. ord('a') = 97). For example, abc maps to (1,1) because ord('b') - ord('a') = 1 and ord('c') - ord('b') = 1. We need to watch out for the “wraparound” case - for example, 'az' and 'ba' should map to the same “shift group” as a + 1 = b and z + 1 = a. Given the above point, the respective tuples would be (25,) (122 - 97) and (-1,) (79 - 80) and az and ba would map to different groups. This is incorrect. To account for this case, we add 26 to the difference between letters (smallest difference possible is -25, za) and mod by 26. So, (26 + 122 - 97) % 26 and (26 + 79 - 80) % 26 both equal (25,).

class Solution:
    def groupStrings(self, strings: List[str]) -> List[List[str]]:
        hashmap = {}
        
        for s in strings:
            key = ()
            
            for i in range(len(s) - 1):
                circular_difference = 26 + ord(s[i+1]) - ord(s[i])
                key += circular_difference % 26,
            
            hashmap[key] = hashmap.get(key, []) + [s]
            
        return list(hashmap.values())        

Complexity

Time: $O(ab)$ where $a$ is the total number of strings and $b$ is the length of the longest string in strings.
Space: $O(n)$ as the most space we would use is the space required for strings and the keys of our hashmap.

[266/Easy] Palindrome Permutation

Problem

Given a string s, return true if a permutation of the string could form a palindrome.
Example 1:

Input: s = "code"
Output: false

Example 2:

Input: s = "aab"
Output: true

Example 3:

Input: s = "carerac"
Output: true

Constraints:
- 1 <= s.length <= 5000
- s consists of only lowercase English letters.
See problem on LeetCode.

Solution: Set

Iterate over the given string, add the character to the set if it is not there. Remove it when it is.
At the end, if the length of the sets is <= 1, then a permutation of the string could form a palindrome, else it cannot.

class Solution:
    # TC O(n) 
    # SC O(1) 
    # This is bounded (constant),
    def canPermutePalindrome(self, s: str) -> bool:
        sets = set()
        for char in s:
            if char not in sets:
                sets.add(char)
            else:
                sets.remove(char)
        
        return (len(sets) <= 1)   

Complexity

Time: $O(n)$ where $n$ is the number of the character of string
Space: $O(1)$ since the maximum size of the set would be 128 ASCII characters

Solution: Counter

Just check that no more than one character appears an odd number of times. Because if there is one, then it must be in the middle of the palindrome. So we can’t have two of them.

class Solution:
    def canPermutePalindrome(self, s):
        """
        :type s: str
        :rtype: bool
        """
        counter = collections.Counter(s)
        
        odd = 0
        
        for count in counter.values():
            if count % 2:
                odd += 1
            
            if odd > 1:
                return False
        
        return True

Same approach; with a hash table to count the number of occurrence of characters while iterating over the input string:

class Solution:
    def canPermutePalindrome(self, s: str) -> bool:
        # key: Character, value: count
        maps = collections.defaultdict(int)
        for char in s:
            if maps.get(char):
                maps[char] += 1
            else:
                maps[char] = 1
      
        # Traverse over the map to find even number
        count = 0
        for key in maps:
            count += maps[key] %2
            # if maps[key] % 2 == 1:
            #     # Odd number of occurrence
        # if the count is lesser than 2, it is palindrome
        return (count <= 1)  

Complexity

Time: $O(n)$
Space: $O(1)$

Solution: Counter one-liner

def canPermutePalindrome(self, s):
    return sum(v % 2 for v in collections.Counter(s).values()) < 2

Complexity

Time: $O(n)$
Space: $O(1)$

[273/Hard] Integer to English Words

Problem

Convert a non-negative integer num to its English words representation.
Example 1:

Input: num = 123
Output: "One Hundred Twenty Three"

Example 2:

Input: num = 12345
Output: "Twelve Thousand Three Hundred Forty Five"

Example 3:

Input: num = 1234567
Output: "One Million Two Hundred Thirty Four Thousand Five Hundred Sixty Seven"

Constraints:
- 0 <= num <= 2^31 - 1
See problem on LeetCode.

Solution: Brute force with Dictionary

class Solution:
    def __init__(self):
        self.lessThan20 = ["","One","Two","Three","Four","Five","Six","Seven","Eight","Nine","Ten","Eleven","Twelve","Thirteen","Fourteen","Fifteen","Sixteen","Seventeen","Eighteen","Nineteen"]
        self.tens = ["","Ten","Twenty","Thirty","Forty","Fifty","Sixty","Seventy","Eighty","Ninety"]
        self.thousands = ["","Thousand","Million","Billion"]

    def helper(self, num: int) -> str:
        # edge case
        if num == 0:
            return ""
        elif num < 20:
            return self.lessThan20[num] + " "
        elif num < 100:
            return self.tens[num//10] + " " + self.helper(num%10)
        else:
            return self.lessThan20[num//100] + " Hundred " + self.helper(num%100)

    def numberToWords(self, num: int) -> str:
        # edge case
        if num == 0:
            return "Zero"
            
        res = ""
        for i in range(len(self.thousands)):
            if num % 1000 != 0:
                res = self.helper(num%1000) + self.thousands[i] + " " + res
            num //= 1000
        
        return res.strip()

Complexity

Time: $O(n)$ where $n$ is the number of digits
Space: $O(1)$

[290/Easy] Word Pattern

Given a pattern and a string s, find if s follows the same pattern.
Here follow means a full match, such that there is a bijection between a letter in pattern and a non-empty word in s.
Example 1:

Input: pattern = "abba", s = "dog cat cat dog"
Output: true

Example 2:

Input: pattern = "abba", s = "dog cat cat fish"
Output: false

Example 3:

Input: pattern = "aaaa", s = "dog cat cat dog"
Output: false

Constraints:
- 1 <= pattern.length <= 300
- pattern contains only lower-case English letters.
- 1 <= s.length <= 3000
- s contains only lowercase English letters and spaces ' '.
- s does not contain any leading or trailing spaces.
- All the words in s are separated by a single space.
See problem on LeetCode.

Solution: Use a pattern dictionary to track pattern

class Solution:
    def wordPattern(self, pattern: str, s: str) -> bool:
        words, dic = s.split(' '), {}
        if len(words) != len(pattern) or len(set(words)) != len(set(pattern)):
            return False
        
        for i in range(len(words)):
            # new word? add it to our pattern dict
            if words[i] not in dic:
                dic[words[i]] = pattern[i]
            # word in pattern dict but pattern doesn't match
            elif dic[words[i]] != pattern[i]:
                return False
        
        return True

Complexity

Time: $O(n)$ where $n$ is len(words)
Space: $O(n)$ for dic

[311/Medium] Sparse Matrix Multiplication

Problem

Given two sparse matrices mat1 of size m x k and mat2 of size k x n, return the result of mat1 x mat2. You may assume that multiplication is always possible.
Example 1:

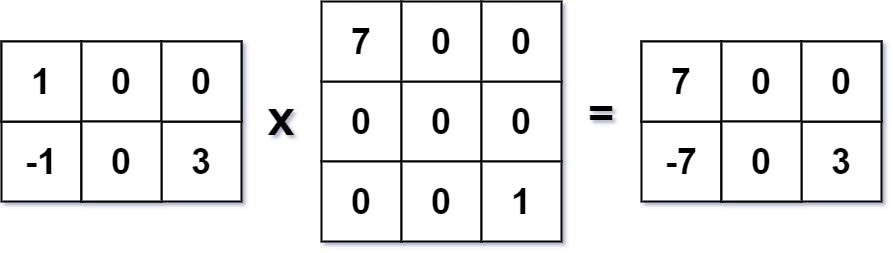
Input: mat1 = [[1,0,0],[-1,0,3]], mat2 = [[7,0,0],[0,0,0],[0,0,1]]
Output: [[7,0,0],[-7,0,3]]

Example 2:

Input: mat1 = [[0]], mat2 = [[0]]
Output: [[0]]

Constraints:
- m == mat1.length
- k == mat1[i].length == mat2.length
- n == mat2[i].length
- 1 <= m, n, k <= 100
- -100 <= mat1[i][j], mat2[i][j] <= 100
See problem on LeetCode.

Solution: Use an if-condition to run the third loop only when we have a non-zero element

class Solution:
    def multiply(self, mat1: List[List[int]], mat2: List[List[int]]) -> List[List[int]]:
        ## For a typical matrix multiplication, solution is without the if condition. but its N^3
        ## However, as this is sparse matrix, most of the elements are 0's. so we can make it efficient to run the third loop only when we have element in mat1 matrix.
        mmat1, nmat1, nmat2 = len(mat1), len(mat1[0]), len(mat2[0])
        res = [[0]*len(mat2[0]) for _ in range(mmat1)]
        for i in range(mmat1):
            for j in range(nmat1):
                if mat1[i][j]:
                    for k in range(nmat2):
                        res[i][k] += mat1[i][j]*mat2[j][k]
        return res

Complexity

Time: $O(n)$ where $n =$len(mat1) x len(mat1[0]) x len(mat2[0])
Space: $O(len(mat1 \times mat2))$

Solution: Store non-zero elements in nested dictionaries and check those while calculating answer

class Solution:
    def multiply(self, mat1: List[List[int]], mat2: List[List[int]]) -> List[List[int]]:    
        ## The above solution is not efficient, so we store non-zero elements in nested hashmaps and checking those while calculating ans
        ## (m1 * n1) x (m2 * n2) = (m1 * n2) [n1 = m2 always, we check the same here while looping through hashmaps]
        m1, n1 = len(mat1), len(mat1[0])
        m2, n2 = len(mat2), len(mat2[0])
        res = [[0 for i in range(n2)] for j in range(m1)]
        X, Y = [dict() for i in range(m1)], [dict() for j in range(n2)]
        
        for i in range(m1):
            for j in range(n1):
                if mat1[i][j] != 0:
                    X[i][j] = mat1[i][j]
        
        for i in range(m2):
            for j in range(n2):
                if mat2[i][j] != 0:
                    # watchout (j,i)
                    Y[j][i] = mat2[i][j]
                    
        for i in range(m1):
            for j in range(n2):
                for r in X[i]:
                    if r in Y[j]:
                        res[i][j] += X[i][r] * Y[j][r]
        return res

Complexity

Time: $O(m1 \cdot n1 + m2 \cdot n2 + m1 \cdot n2)$
Space: $O(len(mat1 \times mat2))$

Solution: Two dictionaries

Given A and B are sparse matrices, we could use lookup tables to speed up. Surprisingly, it seems like detecting non-zero elements for both A and B on the fly without additional data structures provided the fastest performance on current test set.

class Solution(object):
    def multiply(self, mat1, mat2):
        """
        :type mat1: List[List[int]]
        :type mat2: List[List[int]]
        :rtype: List[List[int]]
        """
        if mat1 is None or mat2 is None: return None
        m, n = len(mat1), len(mat1[0])
        if len(mat2) != n:
            raise Exception("mat1's column number must be equal to mat2's row number.")
        l = len(mat2[0])
        table_mat1, table_mat2 = {}, {}
        
        for i, row in enumerate(mat1):
            for j, ele in enumerate(row):
                if ele:
                    if i not in table_mat1: table_mat1[i] = {}
                    table_mat1[i][j] = ele
                    
        for i, row in enumerate(mat2):
            for j, ele in enumerate(row):
                if ele:
                    if i not in table_mat2: table_mat2[i] = {}
                    table_mat2[i][j] = ele
                    
        C = [[0 for j in range(l)] for i in range(m)]
        for i in table_mat1:
            for k in table_mat1[i]:
                if k not in table_mat2: continue
                for j in table_mat2[k]:
                    C[i][j] += table_mat1[i][k] * table_mat2[k][j]
        return C

Complexity

Time: $O(len(mat1) + len(mat2) + len(mat1 \times mat2)) = O(len(mat1 \times mat2))$
Space: $O(len(mat1 \times mat2))$

[325/Medium] Maximum Size Subarray Sum Equals k

Problem

Given an integer array nums and an integer k, return the maximum length of a subarray that sums to k. If there is not one, return 0 instead.
Example 1:

Input: nums = [1,-1,5,-2,3], k = 3
Output: 4
Explanation: The subarray [1, -1, 5, -2] sums to 3 and is the longest.

Example 2:

Input: nums = [-2,-1,2,1], k = 1
Output: 2
Explanation: The subarray [-1, 2] sums to 1 and is the longest.

Constraints:
- 1 <= nums.length <= 2 * 105
- -104 <= nums[i] <= 104
- -109 <= k <= 109
See problem on LeetCode.

Solution: Dictionary

The dictionary stores the sum of all elements from the beginning until index i as key, and i as value. For each i, check not only the currentSum but also (currentSum - previousSum) to see if there is any that equals k, and update max_len.

class Solution:
    def maxSubArrayLen(self, nums: List[int], k: int) -> int:
        sum_to_index_mapping = {} # key: cumulative sum until index i, value: i
        curr_sum = max_len = 0 # set initial values for cumulative sum and max length sum to 0
        
        for i in range(len(nums)):
            curr_sum += nums[i] # update cumulative sum
            
            # two cases where we can update max_len
            if curr_sum == k:
                max_len = max(max_len, i + 1) # case 1: cumulative sum is k, update max_len for sure
            elif curr_sum - k in sum_to_index_mapping:
                max_len = max(max_len, i - sum_to_index_mapping[curr_sum - k]) # case 2: cumulative sum is different from k, but we can truncate a prefix of the array
                
            # store cumulative sum in dictionary, only if it is not seen
            # because only the earlier (thus shorter) subarray is valuable, when we want to get the max_len after truncation
            if curr_sum not in sum_to_index_mapping:
                sum_to_index_mapping[curr_sum] = i
                
        return max_len

Simplified version:

class Solution:
    def maxSubArrayLen(self, nums: List[int], k: int) -> int:
        sum_to_index_mapping = {0: -1} # key: cumulative sum until index i, value: i
        curr_sum = max_len = 0 # set initial values for cumulative sum and max length sum to 0
        
        for i in range(len(nums)):
            curr_sum += nums[i] # update cumulative sum
            
            # update max_len when cumulative sum is different from k, but we can truncate a prefix of the array
            if curr_sum - k in sum_to_index_mapping:
                max_len = max(max_len, i - sum_to_index_mapping[curr_sum - k])
                
            # store cumulative sum in dictionary, only if it is not seen
            # because only the earlier (thus shorter) subarray is valuable, when we want to get the max_len after truncation
            if curr_sum not in sum_to_index_mapping:
                sum_to_index_mapping[curr_sum] = i
                
        return max_len

Complexity

Time: $O(n)$
Space: $O(1)$

[336/Hard] Palindrome Pairs

Problem

Given a list of unique words, return all the pairs of the distinct indices (i, j) in the given list, so that the concatenation of the two words words[i] + words[j] is a palindrome.
Example 1:

Input: words = ["abcd","dcba","lls","s","sssll"]
Output: [[0,1],[1,0],[3,2],[2,4]]
Explanation: The palindromes are ["dcbaabcd","abcddcba","slls","llssssll"]

Example 2:

Input: words = ["bat","tab","cat"]
Output: [[0,1],[1,0]]
Explanation: The palindromes are ["battab","tabbat"]

Example 3:

Input: words = ["a",""]
Output: [[0,1],[1,0]]

Constraints:
- 1 <= words.length <= 5000
- 0 <= words[i].length <= 300
- words[i] consists of lower-case English letters.
See problem on LeetCode.

Solution: Trie

Build a Trie with words. When reach the end of the word, use “isword” to keep the index of the word. During adding a word to the Trie, if the rest of the word is palin, add the index of the word to key “ids” of that node.
Then for each word, look for the reverse of the word in the Trie. During searching for each word, if word ends but the trie path still continues, check the “ids” key of that node (node["ids"] keeps the index of the word which substring is palin after this node).
Check for empty string separately at last.
Current algorithm has a high worst case time complexity, but can be improved to guarantee O(n) (total number of characters of all words). A KMP method is used to calculate the suffix palin for each word in $O(len(word))$, and also for each reverse word. Therefore the ispalin can be check in $O(1)$ after a linear preprocess for each word. However, that solution went TLE. The reason is for the current algorithm, we don’t need to do ispalin check for a good part of cases. However, for that preprocess method, we can’t escape a linear preprocessing.

class TrieNode:
    def __init__(self):
        self.next = collections.defaultdict(TrieNode)
        self.ending_word = -1
        self.palindrome_suffixes = []

class Solution:
    def palindromePairs(self, words):

        # Create the Trie and add the reverses of all the words.
        trie = TrieNode()
        for i, word in enumerate(words):
            word = word[::-1] # We want to insert the reverse.
            current_level = trie
            for j, c in enumerate(word):
                # Check if remainder of word is a palindrome.
                if word[j:] == word[j:][::-1]:# Is the word the same as its reverse?
                    current_level.palindrome_suffixes.append(i)
                # Move down the trie.
                current_level = current_level.next[c]
            current_level.ending_word = i

        # Look up each word in the Trie and find palindrome pairs.
        solutions = []
        for i, word in enumerate(words):
            current_level = trie
            for j, c in enumerate(word):
                # Check for case 3.
                if current_level.ending_word != -1:
                    if word[j:] == word[j:][::-1]: # Is the word the same as its reverse?
                        solutions.append([i, current_level.ending_word])
                if c not in current_level.next:
                    break
                current_level = current_level.next[c]
            else: # Case 1 and 2 only come up if whole word was iterated.
                # Check for case 1.
                if current_level.ending_word != -1 and current_level.ending_word != i:
                    solutions.append([i, current_level.ending_word])
                # Check for case 2.
                for j in current_level.palindrome_suffixes:
                    solutions.append([i, j])
                    
        return solutions

Complexity:

Time: $O(k^2 \cdot n)$ where let $n$ be the number of words, and $k$ be the length of the longest word.
- There were 2 major steps to the algorithm. Firstly, we needed to build the Trie. Secondly, we needed to look up each word in the Trie.
- Inserting each word into the Trie takes O(k)O(k) time. As well as inserting the word, we also checked at each letter whether or not the remaining part of the word was a palindrome. These checks had a cost of $O(k)$, and with $k$ of them, gave a total cost of $O(k^2)$. With $n$ words to insert, the total cost of building the Trie was therefore $O(k^2 \cdot n)$.
- Checking for each word in the Trie had a similar cost. Each time we encountered a node with a word ending index, we needed to check whether or not the current word we were looking up had a palindrome remaining. In the worst case, we’d have to do this $k$ times at a cost of $k$ for each time. So like before, there is a cost of $k^{2k}$ for looking up a word, and an overall cost of $k^2 \cdot nk$ for all the checks.
- This is the same as for the hash table approach.
Space: $O((k + n)^2)$.
- The Trie is the main space usage. In the worst case, each of the $O(n \cdot k)$ letters in the input would be on separate nodes, and each node would have up to nn indexes in its list. This gives us a worst case of $O(n^2 \cdot k)$, which is strictly larger than the input or the output.
- Inserting and looking up words only takes $k$ space though, because we’re not generating a list of prefixes like we were in approach 2. This is insignificant compared to the size of the Trie itself.
- So in total, the size of the Trie has a worst case of $O(k \cdot n^2)$. In practice however, it’ll use a lot less, as we based this on the worst case. Tries are difficult to analyze in the general case, because their performance is so dependent on the type of data going into them. As $n$ gets really, really, big, the Trie approach will eventually beat the hash table approach on both time and space. For the values of nn that we’re dealing with in this question though, you’ll probably notice that the hash table approach performs better.

Solution: check each word for prefixes (and suffixes) that are themselves palindromes

The basic idea is to check each word for prefixes (and suffixes) that are themselves palindromes. If you find a prefix that is a valid palindrome, then the suffix reversed can be paired with the word in order to make a palindrome. Let’s explain with an example.

words = ["bot", "t", "to"]

Starting with the string bot. We start checking all prefixes. If "", "b", "bo", "bot" are themselves palindromes. The empty string and b are palindromes. We work with the corresponding suffixes ("bot", "ot") and check to see if their reverses ("tob", "to") are present in our initial word list. If so (like the word "to"), we have found a valid pairing where the reversed suffix can be prepended to the current word in order to form "to" + "bot" = "tobot".
You can do the same thing by checking all suffixes to see if they are palindromes. If so, then finding all reversed prefixes will give you the words that can be appended to the current word to form a palindrome.
The process is then repeated for every word in the list. Note that when considering suffixes, we explicitly leave out the empty string to avoid counting duplicates. That is, if a palindrome can be created by appending an entire other word to the current word, then we will already consider such a palindrome when considering the empty string as prefix for the other word.

class Solution:
    def palindromePairs(self, words: List[str]) -> List[List[int]]:
        
        lookup = {w:i for i,w in enumerate(words)} # swap key (index) and value (word)
        res = []
        
        for i, w in enumerate(words):
            for j in range(len(w)+1):
                pre, suf = w[:j], w[j:] # prefix and suffix
                
                # consider prefixes
                # 1. note that suf[::-1] != w is there to ensure we do use the current input word (w) 
                # as a suffix since the input words are unique (so we do not have have two of "w")
                # 2. also note that if the prefix slice of the input word is a palindrome, 
                # we need to look for the reversed suffixed (and thus treat it as a prefix)
                # and add it as the first element in the tuple (since it is a prefix for our result) 
                if pre == pre[::-1] and suf[::-1] != w and suf[::-1] in lookup:
                    res.append([lookup[suf[::-1]], i]) # palindrome prefix e.g. 'lls' and 's', 'sssll' and 'lls' in Example 1
                        
                # consider suffixes
                # 1. note that pre[::-1] != w is there to ensure we do use the current input word (w) 
                # as a prefix since the input words are unique (so we do not have have two of "w")
                # 2. also note that if the suffix slice of the input word is a palindrome, 
                # we need to look for the reversed prefix (and thus treat it as a suffix)
                # and add it as the second element in the tuple (since it is a suffix for our result) 
                if j != len(w) and suf == suf[::-1] and pre[::-1] != w and pre[::-1] in lookup: # j==len(w) case is already checked above
                    res.append([i, lookup[pre[::-1]]]) # palindrome suffix e.g. 'sll' and 's'
        
        return res

Complexity

Time: $O(n * m)$ where $n$ is the length of words and $m$ is the average length of the words in words
Space: $O(n)$ for res, pre, suf, lookup

[340/Medium] Longest Substring with At Most K Distinct Characters

Problem

Given a string s and an integer k, return the length of the longest substring of s that contains at most k distinct characters.
Example 1:

Input: s = "eceba", k = 2
Output: 3
Explanation: The substring is "ece" with length 3.

Example 2:

Input: s = "aa", k = 1
Output: 2
Explanation: The substring is "aa" with length 2.

Constraints:
- 1 <= s.length <= 5 * 104
- 0 <= k <= 50
See problem on LeetCode.

Solution: Two pointers + Hashmap

Use a hashmap to maintain count for the number of seen distinct characters.
Maintain a sliding window with two pointers start and end.
The idea is to first build a window starting from the left. Then as soon as we have more distinct characters in the window than k, we trim it from the left end.

class Solution:
    def lengthOfLongestSubstringKDistinct(self, s: str, k: int) -> int:
        seen = Counter()
        start = 0
        maxCount = 0
        
        # sliding window from start to end
        for end, char in enumerate(s):
            # saw a char? add it to our hashmap
            seen[char] += 1
            
            # do you have more chars than what we need?
            while len(seen) > k:
                # start removing character from left
                leftChar = s[start]
                seen[leftChar] -= 1
                
                # if count for a char is 0, delete it from our hashmap
                if seen[leftChar] == 0:
                    del seen[leftChar]
                    
                # move the left pointer ahead
                start += 1
                
            # current window
            count = end - start + 1
            maxCount = max(count, maxCount)
        
        return maxCount

Complexity

Time: $O(kn) = O(n)$
Space: $O(n)$ due to seen

[348/Medium] Design Tic-Tac-Toe

Problem

Assume the following rules are for the tic-tac-toe game on an n x n board between two players:
- A move is guaranteed to be valid and is placed on an empty block.
- Once a winning condition is reached, no more moves are allowed.
- A player who succeeds in placing n of their marks in a horizontal, vertical, or diagonal row wins the game.
Implement the TicTacToe class:
- TicTacToe(int n) Initializes the object the size of the board n.
- int move(int row, int col, int player) Indicates that the player with id player plays at the cell (row, col) of the board. The move is guaranteed to be a valid move.
Example 1:

Input
["TicTacToe", "move", "move", "move", "move", "move", "move", "move"]
[[3], [0, 0, 1], [0, 2, 2], [2, 2, 1], [1, 1, 2], [2, 0, 1], [1, 0, 2], [2, 1, 1]]
Output
[null, 0, 0, 0, 0, 0, 0, 1]
Explanation
TicTacToe ticTacToe = new TicTacToe(3);
Assume that player 1 is "X" and player 2 is "O" in the board.
ticTacToe.move(0, 0, 1); // return 0 (no one wins)
|X| | |
| | | |    // Player 1 makes a move at (0, 0).
| | | |

ticTacToe.move(0, 2, 2); // return 0 (no one wins)
|X| |O|
| | | |    // Player 2 makes a move at (0, 2).
| | | |

ticTacToe.move(2, 2, 1); // return 0 (no one wins)
|X| |O|
| | | |    // Player 1 makes a move at (2, 2).
| | |X|

ticTacToe.move(1, 1, 2); // return 0 (no one wins)
|X| |O|
| |O| |    // Player 2 makes a move at (1, 1).
| | |X|

ticTacToe.move(2, 0, 1); // return 0 (no one wins)
|X| |O|
| |O| |    // Player 1 makes a move at (2, 0).
|X| |X|

ticTacToe.move(1, 0, 2); // return 0 (no one wins)
|X| |O|
|O|O| |    // Player 2 makes a move at (1, 0).
|X| |X|

ticTacToe.move(2, 1, 1); // return 1 (player 1 wins)
|X| |O|
|O|O| |    // Player 1 makes a move at (2, 1).
|X|X|X|

Constraints:
- 2 <= n <= 100
- player is 1 or 2.
- 0 <= row, col < n
- (row, col) are unique for each different call to move.
- At most n2 calls will be made to move.
Follow-up: Could you do better than O(n^2) per move() operation?
See problem on LeetCode.

Solution: Counter to track each row, column and both diag counts for each player

Create a Counter to track each row, column and both diag counts for each player. Here, (row, col, row+col, row-col) means (row, col, diag, anti-diag).
In other words, the idea is that you can uniquely identify diagonals by row - col, and anti-diagonals by row + col.
The counter is per type per player.

class TicTacToe(object):
    def __init__(self, n):
        count = collections.Counter()
        def move(row, col, player):
            for i, x in enumerate((row, col, row+col, row-col)):
                count[i, x, player] += 1
                if count[i, x, player] == n:
                    return player
            return 0
        self.move = move

Complexity

Time: $O(1)$
Space: $O(n)$

Solution: Four loops, one for each of row, col, diag and anti-diag

class TicTacToe:
    def __init__(self, n: int):
        self.board = [ [0] * n for i in range(n) ]
        self.size = n     

    def move(self, row: int, col: int, player: int) -> int:
        if self.board[row][col] == 0: self.board[row][col] = player
        
        for i in range(self.size):
            if self.board[row][i] != player: break
        else: return player
        
        for i in range(self.size):
            if self.board[i][col] != player: break
        else: return player
            
        for i in range(self.size):
            if self.board[i][i] != player: break
        else: return player
        
        for i in range(self.size):
            if self.board[self.size-i-1][i] != player: break
        else: return player
        
        return 0   

Same approach; concise:

class TicTacToe:

    def __init__(self, n: int):
        self.board, self.size = [[0] * n for _ in range(n)], n
        
    def move(self, row: int, col: int, player: int) -> int:
        if self.board[row][col] != 0: 
            return 0
        
        self.board[row][col] = player
        
        def r()-> bool:
            return sum(1 for j in range(self.size) if self.board[row][j] == player) == self.size

        def c() -> bool:
            return sum(1 for i in range(self.size) if self.board[i][col] == player) == self.size

        def d() -> bool:
            return sum(1 for i in range(self.size) if self.board[i][i] == player) == self.size

        def ad() -> bool:
            return sum(1 for i in range(self.size - 1, -1, -1) if self.board[i][self.size - i - 1] == player) == self.size
        
        return player if (r() or c() or d() or ad()) else 0

Complexity

Time: $O(1)$
Space: $O(n)$

Solution: Use a list/hash table to record the occurrence for each rows, cols and two diagonals

Algorithm:
- There are only n (rows) + n (cols) + 2 (diagonals) ways to win the game.
- So use a list or hash table to record the occurrence.
- For player 1, +1; for player 2, -1, verify the value after each call to determine the winner.

class TicTacToe:
    def __init__(self, n: int):
        self.n = n
        self.row = [0] * n
        self.col = [0] * n
        self.dia = [0] * 2

    def move(self, row: int, col: int, player: int) -> int:
        if player == 1:
            self.row[row] += 1
            self.col[col] += 1
            if row == col: 
                self.dia[0] += 1
            if row + col == self.n-1: 
                self.dia[1] += 1
            if self.row[row] == self.n or self.col[col] == self.n or self.dia[0] == self.n or self.dia[1] == self.n:
                return 1
        else:     
            self.row[row] -= 1
            self.col[col] -= 1
            if row == col: 
                self.dia[0] -= 1
            if row + col == self.n-1: 
                self.dia[1] -= 1
            if self.row[row] == -self.n or self.col[col] == -self.n or self.dia[0] == -self.n or self.dia[1] == -self.n: 
                return 2
        return 0

Complexity

Time: $O(1)$
Space: $O(n)$

[380/Medium] Insert Delete GetRandom O(1)

Problem

Implement the RandomizedSet class:
- RandomizedSet() Initializes the RandomizedSet object.
- bool insert(int val) Inserts an item val into the set if not present. Returns true if the item was not present, false otherwise.
- bool remove(int val) Removes an item val from the set if present. Returns true if the item was present, false otherwise.
- int getRandom() Returns a random element from the current set of elements (it’s guaranteed that at least one element exists when this method is called). Each element must have the same probability of being returned.
You must implement the functions of the class such that each function works in average O(1) time complexity.
Example 1:

Input
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]

Output

[null, true, false, true, 2, true, false, 2]

Explanation:

RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomizedSet.remove(2); // Returns false as 2 does not exist in the set.
randomizedSet.insert(2); // Inserts 2 to the set, returns true. Set now contains [1,2].
randomizedSet.getRandom(); // getRandom() should return either 1 or 2 randomly.
randomizedSet.remove(1); // Removes 1 from the set, returns true. Set now contains [2].
randomizedSet.insert(2); // 2 was already in the set, so return false.
randomizedSet.getRandom(); // Since 2 is the only number in the set, getRandom() will always return 2.

Constraints:
- -2^31 <= val <= 2^31 - 1
- At most 2 * 105 calls will be made to insert, remove, and getRandom.
- There will be at least one element in the data structure when getRandom is called.
See problem on LeetCode.

Solution: Dictionary

In order to have O(1) insert and remove operations, we need an unordered set or dict.
In order to have O(1) getRandom operations, we need a data structure with random access. That means we need a list (or vector in C). The hardest part is connecting the two.
What we can do is have a dictionary that for every value we store the index in the list of that value. This way, when we need to remove an element by its value, we know what element from the list to remove without having to traverse the whole list.
Removing an element from the middle of the list while preserving the order of everything else is O(n). But we don’t need to preserve the order. So when removing an element from the middle of the list, we can just swap it with the last element of the list, then remove the last element of the list. This makes the remove operation O(1) as whole. Care must be taken to maintain the dictionary of indexes for the swap!

class RandomizedSet:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.index = {}
        self.elems = []

    def insert(self, val: int) -> bool:
        """
        Inserts a value to the set. Returns true if the set did not already contain the specified element.
        """
        
        # New element will be at the end of list
        if val not in self.index:
            # assign last element idx to the val
            self.index[val] = len(self.elems)
            self.elems.append(val)
            return True
        
        # if val was already in self.index
        return False
    
    def remove(self, val: int) -> bool:
        """
        Removes a value from the set. Returns true if the set contained the specified element.
        """
        if val not in self.index:
            return False
        
        # We're overwriting the element to be removed with the last element in the list.
        # In other words, the last element will move to the position of the element to be removed.
        # We then pop the last element.
        if self.elems[-1] != val: # or if self.index[val] < len(self.elems)-1: # Make sure we're not already at the last element.
            # update index of the last element to be the index of val
            self.index[self.elems[-1]] = self.index[val]
            
            # overwrite the last element to the position of the val
            self.elems[self.index[val]] = self.elems[-1]

        # Remove the last element. This is O(1).
        self.elems.pop()
        
        # The removed element no longer has an index in the list. Update dictionary.
        self.index.pop(val) # or del self.index[val]
            
        return True

    def getRandom(self) -> int:
        """
        Get a random element from the set.
        """
        return random.choice(self.elems)

Complexity

Time:
- Insert: $O(1)$
- Remove: $O(1)$
- GetRandom: $O(1)$
Space: $O(n)$ where $n$ is the size of the dictionary.

[381/Medium] Insert Delete GetRandom O(1) - Duplicates allowed

Problem

RandomizedCollection is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also removing a random element.
Implement the RandomizedCollection class:
- RandomizedCollection() Initializes the empty RandomizedCollection object.
- bool insert(int val) Inserts an item val into the multiset, even if the item is already present. Returns true if the item is not present, false otherwise.
- bool remove(int val) Removes an item val from the multiset if present. Returns true if the item is present, false otherwise. Note that if val has multiple occurrences in the multiset, we only remove one of them.
- int getRandom() Returns a random element from the current multiset of elements. The probability of each element being returned is linearly related to the number of same values the multiset contains.
You must implement the functions of the class such that each function works on average O(1) time complexity.
Note: The test cases are generated such that getRandom will only be called if there is at least one item in the RandomizedCollection.
Example 1:

Input
["RandomizedCollection", "insert", "insert", "insert", "getRandom", "remove", "getRandom"]
[[], [1], [1], [2], [], [1], []]
Output
[null, true, false, true, 2, true, 1]

Explanation
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1);   // return true since the collection does not contain 1.
                                  // Inserts 1 into the collection.
randomizedCollection.insert(1);   // return false since the collection contains 1.
                                  // Inserts another 1 into the collection. Collection now contains [1,1].
randomizedCollection.insert(2);   // return true since the collection does not contain 2.
                                  // Inserts 2 into the collection. Collection now contains [1,1,2].
randomizedCollection.getRandom(); // getRandom should:
                                  // - return 1 with probability 2/3, or
                                  // - return 2 with probability 1/3.
randomizedCollection.remove(1);   // return true since the collection contains 1.
                                  // Removes 1 from the collection. Collection now contains [1,2].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.

Constraints:
- -231 <= val <= 231 - 1
- At most 2 * 105 calls in total will be made to insert, remove, and getRandom.
- There will be at least one element in the data structure when getRandom is called.
See problem on LeetCode.

Solution: Dictionary

In order to have O(1) insert and remove operations, we need an unordered set or dict.
In order to have O(1) getRandom operations, we need a data structure with random access. That means we need a list (or vector in C). The hardest part is connecting the two.
What we can do is have a default dictionary (a regular dict can work too, every time you encounter a new key val, initialize a new set using set() as the value for that key) that for every value we store the index in the list of that value. This way, when we need to remove an element by its value, we know what element from the list to remove without having to traverse the whole list.
Removing an element from the middle of the list while preserving the order of everything else is O(n). But we don’t need to preserve the order. So when removing an element from the middle of the list, we can just swap it with the last element of the list, then remove the last element of the list. This makes the remove operation O(1) as whole. Care must be taken to maintain the dictionary of indexes for the swap!

from collections import defaultdict
from random import choice

class RandomizedCollection:
    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.elems = []
        self.index = defaultdict(set)

    def insert(self, val: int) -> bool:
        """
        Inserts a value to the collection. Returns true if the collection did not already contain the specified element.
        """
        # Stores the indexes of the "val" inserted in the dictionary and also append this val randomly to the elems 
        self.index[val].add(len(self.elems))
        self.elems.append(val)
        return len(self.index[val]) == 1


    def remove(self, val: int) -> bool:
        """
        Removes a value from the collection. Returns true if the collection contained the specified element.
        """
        # remove "val" from the postions or indexes by virtual swapping i.e. the index to be removed is placed with the "last " element  value and the popped index is then use to add to
        # "last" elemnt in dict to occupy the postition of "deleted 'val'" and and "last" element postion in self.elems is removed from dict and elems subsequntly
        
        if not self.index[val]: 
            return False
        
        # We're overwriting the element to be removed with the last element in the list.
        # In other words, the last element will move to the position of the element to be removed.
        # We then pop the last element.

        # the pop() method removes a random item from the set. 
        val_idx = self.index[val].pop()
        last = self.elems[-1]
                
        # overwrite the last element to the position of the val
        self.elems[val_idx] = last        

        # update index of the last element to be the index of val
        self.index[last].add(val_idx)

        # the last element has now moved to val_idx; so remove the "last" (len(self.elems)-1) index corresponding to the last elem
        # note that the set.remove() method raises an error when the specified element doesn't exist in the given set, 
        # however the discard() method doesn't raise any error if the specified element is not present in the set 
        # and the set remains unchanged, i.e., it fails silently.
        self.index[last].discard(len(self.elems) - 1)            

        # Remove the last element. This is O(1).
        self.elems.pop()
                    
        return True        

    def getRandom(self) -> int:
        """
        Get a random element from the collection.
        """
        return choice(self.elems)
        
# Your RandomizedCollection object will be instantiated and called as such:
# obj = RandomizedCollection()
# param_1 = obj.insert(val)
# param_2 = obj.remove(val)
# param_3 = obj.getRandom()        

Complexity

Time:
- Insert: $O(1)$
- Remove: $O(1)$
- GetRandom: $O(1)$
Space: $O(n)$ where $n$ is the size of the dictionary.

[498/Medium] Diagonal Traverse

Problem

Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.
Example 1:

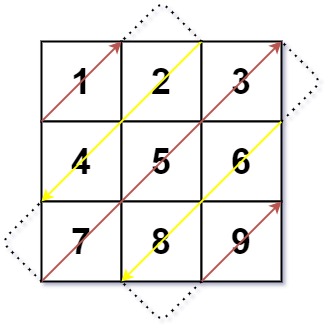
Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]

Example 2:

Input: mat = [[1,2],[3,4]]
Output: [1,2,3,4]

Constraints:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 104
- 1 <= m * n <= 104
- -105 <= mat[i][j] <= 105
See problem on LeetCode.

Solution: Sum of indices = Diagonal

The key here is to realize that the sum of indices on all diagonals are equal.
For example, in the input below, 2, 4 are on the same diagonal, and they share the index sum of 1. (2 is matrix[0][1] and 4 is in matrix[1][0]). 3,5,7 are on the same diagonal, and they share the sum of 2. (3 is matrix[0][2], 5 is matrix[1][1], and 7 is matrix [2][0]).

[1,2,3]
[4,5,6]
[7,8,9]

So, if you can loop through the matrix, store each element by the sum of its indices in a dictionary, you have a collection of all elements on shared diagonals.
The last part is easy, build your answer (a list) by elements on diagonals. To capture the ‘zig zag’ or ‘snake’ phenomena of this problem, simply reverse ever other diagonal level. So check if the level is divisible by 2.
Takeaways:
1. Diagonals are defined by the equal sum of indices in a 2-dimensional array.
2. The snake phenomena can be achieved by reversing every other diagonal level, therefore check if divisible by 2.

class Solution(object):
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
        """
        d={}
        #loop through matrix
        for i in range(len(matrix)):
            for j in range(len(matrix[i])):
                #if no entry in dictionary for sum of indices aka the diagonal, create one
                if i + j not in d:
                    d[i+j] = [matrix[i][j]]
                else:
                #If you've already passed over this diagonal, keep adding elements to it!
                    d[i+j].append(matrix[i][j])
                    
        # we're done with the pass, let's build our answer array
        ans= []
        #look at the diagonal and each diagonal's elements
        for entry in d.items():
            #each entry looks like (diagonal level (sum of indices), [elem1, elem2, elem3, ...])
            #snake time, look at the diagonal level
            if entry[0] % 2 == 0:
                #Here we append in reverse order because its an even numbered level/diagonal. 
                [ans.append(x) for x in entry[1][::-1]]
            else:
                [ans.append(x) for x in entry[1]]
                
        return ans

Same approach; cleaner solution:

from collections import defaultdict
class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        R, C = len(mat), len(mat[0])
        diagonalDict = defaultdict(list)
        
        # key - diagonal elements have the same r + c value.
        for r in range(R):
            for c in range(C):
                diagonalDict[r+c].append(mat[r][c])
                
        ans = []
        for i, value in enumerate(diagonalDict.values()):
            if i % 2 == 0:
                ans += value[::-1]
            else:
                ans += value
                
        return ans

[560/Medium] Subarray Sum Equals $K$

Problem

Given an array of integers nums and an integer k, return the total number of subarrays whose sum equals to k.
Example 1:

Input: nums = [1,1,1], k = 2
Output: 2

Example 2:

Input: nums = [1,2,3], k = 3
Output: 2

Constraints:
- 1 <= nums.length <= 2 * 104
- -1000 <= nums[i] <= 1000
- -107 <= k <= 107
See problem on LeetCode.

Solution: Dictionary

Algorithm:
- First of all, the basic idea behind this code is that, whenever the sums has increased by a value of k, we’ve found a subarray of sums=k.
- But why do we need to initialize a 0 in the hashmap?
- Example: Let’s say our elements are [1,2,1,3] and k = 3 and our corresponding running sums = [1,3,4,7]
- Now, if you notice the running sums array, from 1->4, there is increase of k and from 4->7, there is an increase of k. So, we’ve found 2 subarrays of sums=k.
- But, if you look at the original array, there are 3 subarrays of sums==k. Now, you’ll understand why 0 comes in the picture.
- In the above example, 4-1=k and 7-4=k. Hence, we concluded that there are 2 subarrays.
- However, if sums==k, it should’ve been 3-0=k. But 0 is not present in the array. To account for this case, we include the 0.
- Now the modified sums array will look like [0,1,3,4,7]. Now, try to see for the increase of k.
```
  0->3
  1->4
  4->7
```
- Hence, 3 sub arrays of sums=k.
Comments:
- I:
  - Single scan. Given the current sum and the k, we check if (sum-k) existed as previous sum at an earlier stage (aka smaller window size)
  - Keep expanding the sum while checking whether we have seen (sum - k) before
- II:
  - It’s possible that the freq of a sum could be greater than 1 only when the nums list conatins a zero. For e.g., nums = [1,2,3,0,4]
  - Because sum will be the same for two consecutive iterations.
  - It’s important to capture this edge case in order to return the correct number of subarrays that
  - Add up to target.
  - If we are guaranteed that the list nums has no zeros, then we can replace the prefix dict with a prefix set

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        ans = 0
        prefsum = 0
        d = {0:1}

        for num in nums:
            prefsum = prefsum + num

            if prefsum-k in d: # I
                ans = ans + d[prefsum-k]

            if prefsum not in d:
                d[prefsum] = 1
            else:
                d[prefsum] = d[prefsum]+1 # II

        return ans

Same approach but rehashed:

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        # first we start from a sum which is equal to 0, and the count of it is 1.
        # this is the input list e.g.: [1 4 9 -5 8]
        # this is the sum array (s) e.g.: [0  1    5    13    8    16 ]    

        ans, n = 0, len(nums)
        preSum = 0
        sumDict = {}
        sumDict[0] = 1
        
        for i in nums:
            #we keep adding to the cumulative sums, preSum:
            preSum += i
            
            # we make sure to check if preSum sum - k is already in the dictionary, if so, increase the count.         
            if preSum-k in dic: # I
                ans += sumDict[preSum-k] 
            
            # we check if s is already in the sumDict, if so, increase by 1, if not assign 1.    
            sumDict[preSum] = sumDict.get(preSum, 0) + 1 # II
        
        return ans        

Complexity

Time: $O(n)$
Space: $O(n)$

[621/Medium] Task Scheduler

Problem

Given a characters array tasks, representing the tasks a CPU needs to do, where each letter represents a different task. Tasks could be done in any order. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer n that represents the cooldown period between two same tasks (the same letter in the array), that is that there must be at least n units of time between any two same tasks.
Return the least number of units of times that the CPU will take to finish all the given tasks.
Example 1:

Input: tasks = ["A","A","A","B","B","B"], n = 2
Output: 8
Explanation: 
A -> B -> idle -> A -> B -> idle -> A -> B
There is at least 2 units of time between any two same tasks.

Example 2:

Input: tasks = ["A","A","A","B","B","B"], n = 0
Output: 6
Explanation: On this case any permutation of size 6 would work since n = 0.
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
And so on.

Example 3:

Input: tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
Output: 16
Explanation: 
One possible solution is
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> idle -> idle -> A -> idle -> idle -> A

Constraints:
- 1 <= task.length <= 104
- tasks[i] is upper-case English letter.
- The integer n is in the range [0, 100].
See problem on LeetCode.

Solution: Mathematical model to develop a template and quantify the number of cycles needed; Counter to track most frequent tasks

Take the maximum frequency element and make those many number of slots/groups with each slot/group sized n+1.
- Slot size = (n+1). Therefore, if n = 2 => slot size = 3 . For e.g., {A:5, B:1} => ABxAxxAxxAxxAxx => indices of A = 0,2 and middle there should be n elements, so slot size should be n+1.
  - As an example: ``` tasks = [“A”,”A”,”A”,”B”,”B”,”B”], n = 2
  Procedure:
  
  1. # Build a dictionary for tasks # key : task # value : occurrence of task
  
  max_occ = 3
  
  number_of_taks_of_max_occ = 2 with {‘A’, ‘B’}
  
  2. #Make (max_occ - 1) = 2 groups, groups size = n+1 = 3 #Fill each group with uniform iterleaving as even as possible
  
  group = ‘_ _ _’ with size = 3
  
  => make 2 groups with uniform iterleaving
  
  A B _ A B _
  
  3. # At last, execute for the last time of max_occ jobs
  
  A B _ A B _ A B
  
  length of task scheduling with cooling = 8
```
  - Another example:
```
  ## Ex: {A:6,B:4,C:2} n = 2 ## final o/p will be ## slot size / cycle size = 3 ## Number of rows = number of A’s (most freq element) # [ # [A, B, C], # [A, B, C], # [A, B, idle], # [A, B, idle], # [A, idle, idle], # [A - - ], # ] # # so from above total time intervals = (max_freq_element - 1) * (n + 1) + (all elements with max freq) # ans = rows_except_last * columns + last_row ```
- But consider {A:5, B:1, C:1, D:1, E:1, F:1, G:1, H:1, I:1, J:1, K:1, L:1}; n = 1 as an input. In this case, the total time intervals by above formula will be 4 * 2 + 1 = 9, which is less than number of elements, which is not possible. So we have to return max(ans, number of tasks).

class Solution:
    def leastInterval(self, tasks: List[str], n: int) -> int:
      if n == 0:
            # Quick response for special case on n = 0
            # no requirement for cooling, just do those jobs in original order
            return len(tasks)
                    
        # Build a counter with
        # key  : task
        # value: occurrence of tasks                     
        freq = list(collections.Counter(tasks).values())
        
        # max frequency among tasks
        maxFreq = max(freq)
        
        # figure out number of tasks with the max frequency
        maxFreqCount = freq.count(maxFreq)
        
        # Make (maxFreq-1) groups, each groups size is (n+1) to meet the requirement of cooling
        # Fill each group with uniform interleaving as much as possible. 
        # For the last row of the slot matrix, add maxFreqCount jobs        
        ans = (maxFreq - 1) * (n+1) + maxFreqCount
        
        # Minimal length is original length on best case.
        # Otherwise, it need some cooling intervals in the middle (which is accommodated in "ans")
        return max(ans, len(tasks))

Complexity

Time: $O(n)$
Space: $O(1)$

[935/Medium] Knight Dialer

Problem

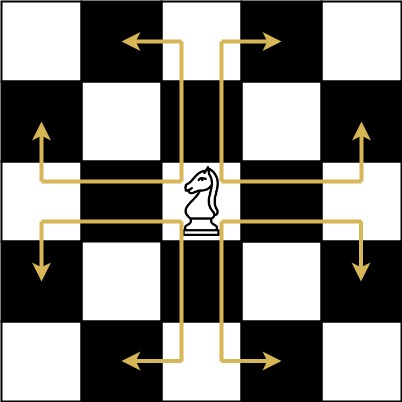
The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:

We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

Given an integer n, return how many distinct phone numbers of length n we can dial.
You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.
As the answer may be very large, return the answer modulo 10^9 + 7.
Example 1:

Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.

Constraints:
- 1 <= n <= 5000
See problem on LeetCode.

Solution: DP

class Solution:
    def knightDialer(self, n: int) -> int:
        # Neighbors maps K: starting_key -> V: list of possible destination_keys
        neighbors = {
            0:(4,6),
            1:(6,8),
            2:(7,9),
            3:(4,8),
            4:(0,3,9),
            5:(),
            6:(0,1,7),
            7:(2,6),
            8:(1,3),
            9:(2,4)
        }
        
        current_counts = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
        for _ in range(n-1):
            next_counts = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
            for src_key in range(10):
                for dst_key in neighbors[src_key]:
                    next_counts[dst_key] = (next_counts[dst_key] + current_counts[src_key]) % (10**9 + 7)
            current_counts = next_counts
            
        return sum(current_counts) % (10**9 + 7)

Blog post from a Googler that explains the background of this question, common pitfalls candidates encounter, four different ways to solve it, and how a Google interviewer will evaluate your solution.

Complexity

Time: $O(n)$
Space: $O(1)$

Solution: Recursion + Memoization

class Solution:
    def knightDialer(self, n: int) -> int:
    # paths represents every key we can go to from given key
    # -1 is starting condition, we can start from any key
        paths = {-1: [0,1,2,3,4,5,6,7,8,9], 0: [4,6], 1: [6,8], 2: [7,9], 
        3: [4,8], 4: [0,3,9], 5: [], 6: [0,1,7], 7: [2,6], 8: [1,3], 9: [2,4] }
        
        return self.helper(paths, n, -1, {}) % (10 ** 9 + 7)
        
    def helper(self, paths, idx, curr, cache):
        if (idx,curr) in cache:
            return cache[(idx,curr)]
        if idx == 0:
            return 1
        
        count = 0
        for num in paths[curr]:
            count += self.helper(paths, idx-1, num, cache)
        
        cache[(idx,curr)] = count
        return count

Complexity

Time: $O(n)$
Space: $O(1)$

Solution: Using NumPy

Algorithm:
- Create a NumPy matrix representing 1 move.
- Subtract 1 from n because the the number of moves is the length of the string minus 1.
- Multiplying that move matrix by itself represents 2 moves.
- Doing that n times, represents 2**n moves.
- Initialize our answer as a 1x10 vector of ones (i.e., one move on each square).
- For each power of 2, if that power of 2 is in n, we add it to our answer.
- Then we create the next power of 2 by multiplying it by itself.
- Mod by 10**9 + 7 (because the question says so).

import numpy as np
MOD = (10**9 + 7)
oneMove = np.zeros((10, 10), dtype=np.int64)
for i, j in ((1, 8), (1, 6), (2, 7), (2, 9), (3, 4), (3, 8), (4, 9), (4, 0), (6, 7), (6, 0)):
    oneMove[i][j] = 1
    oneMove[j][i] = 1
class Solution:
    def knightDialer(self, n: int) -> int:
        n -= 1
        currMove = oneMove
        sumMoves = np.ones((10,), dtype=np.int64)
        while n > 0:
            if n & 1:
                sumMoves = np.matmul(sumMoves, currMove)
                sumMoves = np.mod(sumMoves, MOD)
            n >>= 1
            if n > 0:
                currMove = np.matmul(currMove, currMove)
                currMove = np.mod(currMove, MOD)
        return np.sum(sumMoves) % MOD

Complexity

Time: $O(\log{n})$
Space: $O(1)$

[1147/Medium] Snapshot Array

Problem

Implement a SnapshotArray that supports the following interface:
- SnapshotArray(int length) initializes an array-like data structure with the given length. Initially, each element equals 0.
- void set(index, val) sets the element at the given index to be equal to val.
- int snap() takes a snapshot of the array and returns the snap_id: the total number of times we called snap() minus 1.
- int get(index, snap_id) returns the value at the given index, at the time we took the snapshot with the given snap_id.
Example 1:

Input: ["SnapshotArray","set","snap","set","get"]
[[3],[0,5],[],[0,6],[0,0]]
Output: [null,null,0,null,5]
Explanation: 
SnapshotArray snapshotArr = new SnapshotArray(3); // set the length to be 3
snapshotArr.set(0,5);  // Set array[0] = 5
snapshotArr.snap();  // Take a snapshot, return snap_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0);  // Get the value of array[0] with snap_id = 0, return 5

Constraints:
- 1 <= length <= 50000
- At most 50000 calls will be made to set, snap, and get.
- 0 <= index < length
- 0 <= snap_id < (the total number of times we call snap())
- 0 <= val <= 10^9
See problem on LeetCode.

Solution: Brutal Force

Straight forward solution, actual do snap very time snap is called.
This is quick to access, but take lots of extra space and it takes time to take snap shot, as we need to make a copy.

class SnapshotArray:
    def __init__(self, length: int):
        self.cache = []
        self.d = dict()
        self.i = 0

    def set(self, index: int, val: int) -> None:
        self.d[index] = val

    def snap(self) -> int:
        self.cache.append(dict(self.d))
        self.i += 1
        return self.i-1

    def get(self, index: int, snap_id: int) -> int:
        snap = self.cache[snap_id]
        return snap[index] if index in snap else 0

Solution: `defaultdict` + `OrderedDict` + Binary Search

Take individual snap shot when set is called, increment snap id (self.i), when snap is called
This is fast to set and snap but relatively slow when you do an get.
- Even if it’s binary search, make keys indexable take time.
It saves space too!

class SnapshotArray:
    def __init__(self, length: int):
        self.cache = collections.defaultdict(lambda : collections.OrderedDict())
        self.i = 0

    def set(self, index: int, val: int) -> None:
        self.cache[index][self.i] = val

    def snap(self) -> int:
        self.i += 1
        return self.i-1
        
    @lru_cache(maxsize=None)    
    def get(self, index: int, snap_id: int) -> int:
        if index not in self.cache: return 0
        else:
            idx_cache = self.cache[index]
            if snap_id in idx_cache: return idx_cache[snap_id]
            else:
                keys = list(idx_cache.keys()) 
                i = bisect.bisect(keys, snap_id)
                if snap_id > keys[-1]: return idx_cache[keys[-1]]
                elif i == 0: return 0
                else: return idx_cache[keys[i-1]]

Solution: List of lists + Binary Search

A combination of two approaches above:
Space used in greater than approach #2 and less than approach #1.
Fast to set and snap, get speed should be faster than apporach #2 but slower than approach #1.

class SnapshotArray(object):
    def __init__(self, n):
        self.cache = [[[-1, 0]] for _ in range(n)]
        self.i = 0

    def set(self, index, val):
        self.cache[index].append([self.i, val])

    def snap(self):
        self.i += 1
        return self.i - 1

    @lru_cache(maxsize=None)
    def get(self, index, snap_id):
        i = bisect.bisect(self.cache[index], [snap_id + 1]) - 1
        return self.cache[index][i][1]  

Solution: Dictionary

class SnapshotArray:

    def __init__(self, length: int):
        self.d = {}
        self.snap_d = {}
        self.snap_times = -1

    def set(self, index: int, val: int) -> None:
        self.d[index] = val

    def snap(self) -> int:
        self.snap_times += 1
        self.snap_d[self.snap_times] = self.d.copy()
        return self.snap_times

    def get(self, index: int, snap_id: int) -> int:
        if snap_id in self.snap_d:
            d_at_snap = self.snap_d[snap_id]
            if index in d_at_snap:
                return d_at_snap[index]
                
        return 0

# Your SnapshotArray object will be instantiated and called as such:
# obj = SnapshotArray(length)
# obj.set(index,val)
# param_2 = obj.snap()
# param_3 = obj.get(index,snap_id)

[1169/Medium] Invalid Transactions

Problem

A transaction is possibly invalid if:
- the amount exceeds $1000, or;
- if it occurs within (and including) 60 minutes of another transaction with the same name in a different city.
You are given an array of strings transaction where transactions[i] consists of comma-separated values representing the name, time (in minutes), amount, and city of the transaction.
Return a list of transactions that are possibly invalid. You may return the answer in any order.
Example 1:

Input: transactions = ["alice,20,800,mtv","alice,50,100,beijing"]
Output: ["alice,20,800,mtv","alice,50,100,beijing"]
Explanation: The first transaction is invalid because the second transaction occurs within a difference of 60 minutes, have the same name and is in a different city. Similarly the second one is invalid too.

Example 2:

Input: transactions = ["alice,20,800,mtv","alice,50,1200,mtv"]
Output: ["alice,50,1200,mtv"]

Example 3:

Input: transactions = ["alice,20,800,mtv","bob,50,1200,mtv"]
Output: ["bob,50,1200,mtv"]

Constraints:
- transactions.length <= 1000
- Each transactions[i] takes the form "{name},{time},{amount},{city}"
- Each {name} and {city} consist of lowercase English letters, and have lengths between 1 and 10.
- Each {time} consist of digits, and represent an integer between 0 and 1000.
- Each {amount} consist of digits, and represent an integer between 0 and 2000.
See problem on LeetCode.

Solution: Dictionary

Record all transactions done at a particular time. Recording the person and the location.

{time: {person: {location}, person2: {location1, location2}}, time: {person: {location}}}
Example:
['alice,20,800,mtv', 'bob,50,1200,mtv', 'bob,20,100,beijing']

{   
20: {'alice': {'mtv'}, 'bob': {'beijing'}}, 
50: {'bob': {'mtv'}}
} 

For each transaction, check if the amount is invalid - and add it to the invalid transactions if so.
For each transaction, go through invalid times (+-60), check if a transaction by the same person happened in a different city - and add it to the invalid transactions if so.

class Solution:
    def invalidTransactions(self, transactions: List[str]) -> List[str]:        
        transactions_by_name = {}
        
        for transaction in transactions:
            name, time, amount, city = transaction.split(',')
            if name in transactions_by_name:
                transactions_by_name[name].add((int(time), city))
            else:
                transactions_by_name[name] = {(int(time), city)}
        
        invalid = []
        
        for transaction in transactions:
            name, time, amount, city = transaction.split(',')
            if int(amount) > 1000:
                invalid.append(transaction)
            elif self.isInvalid(int(time), city, transactions_by_name[name]):
                invalid.append(transaction) # Only want to append once because it will eventually get to the other transaction and look it up
            
        return invalid
    
    def isInvalid(self, time, city, transactions_by_name):
        for current_time, current_city in transactions_by_name:
            if city != current_city and time in range(current_time-60, current_time+61):
                return True
        return False

Similar approach; streamlined:

class Solution(object):
    def invalidTransactions(self, transactions):
        """
        :type transactions: List[str]
        :rtype: List[str]
        
        memo = dictionary --> create a dictionary to keep track of previous transaction 
        invalid_tran = set --> to store invalid transaction / I use set to avoid duplication 
        
        Iterate over transactions:
            -> if the amount is greater than 1000 add it to the invalid_tran
            -> if there is any other previous transaction done by similar person , check it from the memo
                    -> bring all previous transaction done by similar person (iterate over the memo)
                            -> check if the absolute time difference is less than 60 and the city is the same 
                                    -> if that is true add it to the invalid transaction 
            -> add the transaction to the dictionary (memo) - always keep track of previous transaction 
        """
        import collections
        if not transactions:
            return []
        
        memo = collections.defaultdict(list)    #create a dictionary to keep track of previous transaction 
        invalid_tran = set()                    #to store invalid transaction / I use set to avoid duplication
        for i,transaction  in enumerate (transactions):
            
            name, time, amount, city = (int(i) if i.isnumeric() else i for i in transaction.split(','))
            
            if amount > 1000:                   #if the amount is greater than 1000 add it to the invalid_tran
                invalid_tran.add(transaction)               
                 
            if name in memo:                    # if there is any other previous transaction done by similar person , check it from the memo
                for tran in memo[name]:         # bring all previous transaction done by similar person (iterate over the memo)
                    _, prev_time, _, prev_city =(int(i) if i.isnumeric() else i for i in  tran.split(','))
                    if abs(time-prev_time) <= 60 and prev_city != city:  #check if the absolute time difference is less than 60 and the city is the same
                        invalid_tran.add(tran) 
                        invalid_tran.add(transaction)                    
            
            memo[name].append(transaction)  # add the transaction to the dictionary (memo) - always keep track of previous transaction 
        return invalid_tran

Complexity

Time: $O(n)$
Space: $O(n)$

[1198/Medium] Find Smallest Common Element in All Rows

Given an m x n matrix mat where every row is sorted in strictly increasing order, return the smallest common element in all rows.
If there is no common element, return -1.
Example 1:

Input: mat = [[1,2,3,4,5],[2,4,5,8,10],[3,5,7,9,11],[1,3,5,7,9]]
Output: 5

Example 2:

Input: mat = [[1,2,3],[2,3,4],[2,3,5]]
Output: 2

Constraints:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 500
- 1 <= mat[i][j] <= 104
- mat[i] is sorted in strictly increasing order.
See problem on LeetCode.

Solution: Set intersection

    # 568 ms, set
    def smallestCommonElement1(self, mat: List[List[int]]) -> int:
        s = set(mat[0])
        
        for arr in mat[1:]:
            s = s.intersection(arr)
            
        return s.pop() if s else -1

Solution: Binary search all values in the first array, check if they’re in other arrays

# 544 ms, binary search
class Solution:
    def smallestCommonElement(self, mat: List[List[int]]) -> int:
        # simple binary search
        def is_in_array(val, arr):
            lo, hi = 0, len(arr) - 1
            
            while lo <= hi:
                mid = (lo + hi)//2
                if val == arr[mid]: return 1 # return "found"
                elif val >= arr[mid]: lo = mid + 1
                else: hi = mid - 1
                
            return 0 # return "not found"
            
        # loop through each val in first array
        for num in mat[0]:
            for arr in mat[1:]:
                if not is_in_array(num, arr):
                    break 
            else:
                # this occurs only when there is no break for a num in mat[0]
                return num 
                
        return -1

Complexity

Time: $O(nm\log{n})$
Space: $O(n)$

Solution: Store all values in a dictionary and keep track of occurrences

# 652 ms, hashmap
class Solution:
    def smallestCommonElement(self, mat: List[List[int]]) -> int:
        D = collections.defaultdict(int) # or c = collections.Counter()
        
        for arr in mat:
            for num in arr:
                D[num] += 1
                if D[num] == len(mat):
                    return num
                    
        return -1    

Complexity

Time: $O(nm)$ where where $n$ is number of numbers in an array, $m$ is number of arrays in matrix
Space: $O(10000)$

[1207/Easy] Unique Number of Occurrences

Problem

Given an array of integers arr, return true if the number of occurrences of each value in the array is unique, or false otherwise.
Example 1:

Input: arr = [1,2,2,1,1,3]
Output: true
Explanation: The value 1 has 3 occurrences, 2 has 2 and 3 has 1. No two values have the same number of occurrences.

Example 2:

Input: arr = [1,2]
Output: false

Example 3:

Input: arr = [-3,0,1,-3,1,1,1,-3,10,0]
Output: true

Constraints:
- 1 <= arr.length <= 1000
- -1000 <= arr[i] <= 1000
See problem on LeetCode.

Solution: Run a counter, loop through values and add unique ones to a list while checking for duplicates

class Solution:
    def uniqueOccurrences(self, arr: List[int]) -> bool:
        count = Counter(arr)
        dup = []
        
        for i in count.values():
            if i not in dup:
                dup.append(i)
            else:
                return False
        
        return True     

Complexity

Time: $O(n)$ where $n$ is number of numbers in the input array
Space: $O(n)$ for dup

[1347/Medium] Minimum Number of Steps to Make Two Strings Anagram

Problem

You are given two strings of the same length s and t. In one step you can choose any character of t and replace it with another character.
Return the minimum number of steps to make t an anagram of s.
An anagram of a string is a string that contains the same characters with a different (or the same) ordering.
Example 1:

Input: s = "bab", t = "aba"
Output: 1
Explanation: Replace the first 'a' in t with b, t = "bba" which is anagram of s.

Example 2:

Input: s = "leetcode", t = "practice"
Output: 5
Explanation: Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.

Example 3:

Input: s = "anagram", t = "mangaar"
Output: 0
Explanation: "anagram" and "mangaar" are anagrams. 

Constraints:
- 1 <= s.length <= 5 * 104
- s.length == t.length
- s and t consist of lowercase English letters only.
See problem on LeetCode.

Solution: Find unique characters in `t`

class Solution:
    def minSteps(self, s: str, t: str) -> int:
        for ch in s:
            # Find and replace only one occurrence of each character in "s" within "t"
            t = t.replace(ch, '', 1)
        
        # The remaining chars are 
        return len(t)

Complexity

Time: $O(n^2)$
Space: $O(n)$

Solution: DefaultDict

Idea: the strings are equal in length
- Replacing is the only operation.
- Find how many characters t and s shares.
- And the remaining would be the needed replacement.
  - Count the letter occurrence in the s.
  - Iterate over t and when you get same letter as in s, subtract it from s.
Return the remaining number of letters in s.

import collections 

class Solution:
    def minSteps(self, s: str, t: str) -> int:
        memo = collections.defaultdict(int)
        # saving the number of occurrence of characters in s
        for char in s:
            memo[char] += 1
            
        count = 0
        for char in t:
            if memo[char]:
                memo[char] -=1 # if char in t is also in memo, subtract that from the counted number
            else:
                count += 1

        # return count #or
        return sum(memo.values())

Complexity

Time: $O(n)$
Space: $O(n)$

Solution: Counter

class Solution:
    def minSteps(self, s: str, t: str) -> int:
        return sum((Counter(t) - Counter(s)).values())

Complexity

Time: $O(n)$
Space: $O(n)$

[1365/Easy] How Many Numbers Are Smaller Than the Current Number

Problem

Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j’s such that j != i and nums[j] < nums[i].
Return the answer in an array.
Example 1:

Input: nums = [8,1,2,2,3]
Output: [4,0,1,1,3]
Explanation: 
For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3). 
For nums[1]=1 does not exist any smaller number than it.
For nums[2]=2 there exist one smaller number than it (1). 
For nums[3]=2 there exist one smaller number than it (1). 
For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2).

Example 2:

Input: nums = [6,5,4,8]
Output: [2,1,0,3]

Example 3:

Input: nums = [7,7,7,7]
Output: [0,0,0,0]

Constraints:
- 2 <= nums.length <= 500
- 0 <= nums[i] <= 100
See problem on LeetCode.

Solution: The number of smaller numbers than the current number is the index of the number in a sorted array

Sort the input array.
Store the mapping of the number to it’s index in the sorted array.
Lookup this index to build the result.

class Solution:
    def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:
        index = {}
        for i, n in enumerate(sorted(nums)):
            if n not in d: 
                index[n] = i
                
        return [index[i] for i in nums]        

Complexity

Time: $O(n)$
Space: $O(n)$ for index

[1507/Easy] Reformat Date

Problem

Given a date string in the form Day Month Year, where:
- Day is in the set {"1st", "2nd", "3rd", "4th", ..., "30th", "31st"}.
- Month is in the set {"Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"}`.
- Year is in the range [1900, 2100].
Convert the date string to the format YYYY-MM-DD, where:
- YYYY denotes the 4 digit year.
- MM denotes the 2 digit month.
- DD denotes the 2 digit day.
Example 1:

Input: date = "20th Oct 2052"
Output: "2052-10-20"

Example 2:

Input: date = "6th Jun 1933"
Output: "1933-06-06"

Example 3:

Input: date = "26th May 1960"
Output: "1960-05-26"

Constraints:
- The given dates are guaranteed to be valid, so no error handling is necessary.
See problem on LeetCode.

Solution: String Formatting

Using .format():

class Solution:
    def reformatDate(self, date: str) -> str:
        day,month,year = date.split()
        months = ('Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec')
        return '{}-{:02}-{:0>2}'.format(year, months.index(month) + 1, day[:-2])

Using f-strings; cleaner:

class Solution:
    def reformatDate(self, date: str) -> str:
        day,month,year = date.split()
        months = ('Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec')
        return f'{year}-{months.index(month) + 1:02}-{day[:-2]:0>2}'

Complexity

Time: $O(n)$
Space: $O(1)$

Solution: Map month to number using a dictionary and use replace

class Solution:
    def reformatDate(self, date: str) -> str:

        list_date = date.split()  

        d = {"Jan" : '01', "Feb": '02'
             , "Mar": '03', "Apr": '04'
             , "May": '05', "Jun": '06'
             , "Jul": '07', "Aug": '08'
             , "Sep": '09', "Oct": '10'
             , "Nov": '11', "Dec": '12'}

        day = list_date[0].replace("th","").replace("nd","").replace("st","").replace("rd","")
        month = list_date[1]
        year = list_date[2]

        if int(day) < 10:
            day = '0'+day

        res = year + '-' + d[month] + '-' + day
        return res

Complexity

Time: $O(n)$
Space: $O(1)$

[1512/Easy] Number of Good Pairs/Number of Identical Pairs

Given an array of integers nums, return the number of good pairs.
A pair (i, j) is called good if nums[i] == nums[j] and i < j.
Example 1:

Input: nums = [1,2,3,1,1,3]
Output: 4
Explanation: There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.

Example 2:

Input: nums = [1,1,1,1]
Output: 6
Explanation: Each pair in the array are good.

Example 3:

Input: nums = [1,2,3]
Output: 0

Constraints:
- 1 <= nums.length <= 100
- 1 <= nums[i] <= 100
See problem on LeetCode.

Solution: Use a defaultdict to hold count of the number of times a number is encountered

from collections import defaultdict

class Solution:
    def numIdenticalPairs(self, nums: List[int]) -> int:
        d = defaultdict(int)
        res = 0
        
        for n in nums:
            res += d[n]
            d[n] += 1
        
        return res

Complexity

Time: $O(n)$
Space: $O(1)$

[1636/Easy] Sort Array by Increasing Frequency

Problem

Given an array of integers nums, sort the array in increasing order based on the frequency of the values. If multiple values have the same frequency, sort them in decreasing order.
Return the sorted array.
Example 1:

Input: nums = [1,1,2,2,2,3]
Output: [3,1,1,2,2,2]
Explanation: '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.

Example 2:

Input: nums = [2,3,1,3,2]
Output: [1,3,3,2,2]
Explanation: '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.

Example 3:

Input: nums = [-1,1,-6,4,5,-6,1,4,1]
Output: [5,-1,4,4,-6,-6,1,1,1]

Constraints:
- 1 <= nums.length <= 100
- -100 <= nums[i] <= 100
See problem on LeetCode.

Solution: built-in sort (2x)

class Solution:
    def frequencySort(self, nums):
        c = Counter(nums)
        
        # reverse sort first to satisfy the requirement: "if multiple values have the same frequency, sort them in decreasing order"
        nums.sort(reverse=True)
        
        nums.sort(key=lambda x: c[x])
        
        return nums

Complexity

Time: $O(n\log{n})$
Space: $O(n)$ for Counter

Solution: One-Liner

class Solution:
    def frequencySort(self, nums):
        return (lambda c: sorted(sorted(nums, reverse=True), key=lambda x: c[x]))(Counter(nums))

Complexity

Time: $O(n\log{n})$
Space: $O(n)$ for Counter

Solution: built-in sort (1x) using a sorting key tuple

class Solution:
    def frequencySort(self, nums):
        
        c = Counter(nums)
        nums.sort(key=lambda x: (c[x], -x))
        
        return nums

Complexity

Time: $O(n\log{n})$
Space: $O(n)$ for Counter

Solution: One-Liner

class Solution:
    def frequencySort(self, nums):
        return (lambda c : sorted(nums, key=lambda x: (c[x], -x)))(Counter(nums))

Complexity

Time: $O(n\log{n})$
Space: $O(n)$ for Counter

[1639/Hard] Number of Ways to Form a Target String Given a Dictionary

Problem

You are given a list of strings of the same length words and a string target.
Your task is to form target using the given words under the following rules:
- target should be formed from left to right.
- To form the ith character (0-indexed) of target, you can choose the kth character of the jth string in words if target[i] = words[j][k].
- Once you use the kth character of the jth string of words, you can no longer use the xth character of any string in words where x <= k. In other words, all characters to the left of or at index k become unusuable for every string.
- Repeat the process until you form the string target.
Notice that you can use multiple characters from the same string in words provided the conditions above are met.
Return the number of ways to form target from words. Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:

Input: words = ["acca","bbbb","caca"], target = "aba"
Output: 6
Explanation: There are 6 ways to form target.
"aba" -> index 0 ("acca"), index 1 ("bbbb"), index 3 ("caca")
"aba" -> index 0 ("acca"), index 2 ("bbbb"), index 3 ("caca")
"aba" -> index 0 ("acca"), index 1 ("bbbb"), index 3 ("acca")
"aba" -> index 0 ("acca"), index 2 ("bbbb"), index 3 ("acca")
"aba" -> index 1 ("caca"), index 2 ("bbbb"), index 3 ("acca")
"aba" -> index 1 ("caca"), index 2 ("bbbb"), index 3 ("caca")

Example 2:

Input: words = ["abba","baab"], target = "bab"
Output: 4
Explanation: There are 4 ways to form target.
"bab" -> index 0 ("baab"), index 1 ("baab"), index 2 ("abba")
"bab" -> index 0 ("baab"), index 1 ("baab"), index 3 ("baab")
"bab" -> index 0 ("baab"), index 2 ("baab"), index 3 ("baab")
"bab" -> index 1 ("abba"), index 2 ("baab"), index 3 ("baab")

Constraints:
- 1 <= words.length <= 1000
- 1 <= words[i].length <= 1000
- All strings in words have the same length.
- 1 <= target.length <= 1000
- words[i] and target contain only lowercase English letters.
See problem on LeetCode.

Solution: Counter/Dictionary

class Solution:
    def numWays(self, words: List[str], target: str) -> int:
        n, mod = len(target), 10**9 + 7
        res = [1] + [0] * n
        
        for i in range(len(words[0])):
            count = collections.Counter(w[i] for w in words)
            for j in range(n - 1, -1, -1):
                res[j + 1] += res[j] * count[target[j]] % mod
                
        return res[n] % mod

Complexity

Time: $O(n^2)$
Space: $O(n)$

[1684/Easy] Count the Number of Consistent Strings

Problem

You are given a string allowed consisting of distinct characters and an array of strings words. A string is consistent if all characters in the string appear in the string allowed.
Return the number of consistent strings in the array words.
Example 1:

Input: allowed = "ab", words = ["ad","bd","aaab","baa","badab"]
Output: 2
Explanation: Strings "aaab" and "baa" are consistent since they only contain characters 'a' and 'b'.

Example 2:

Input: allowed = "abc", words = ["a","b","c","ab","ac","bc","abc"]
Output: 7
Explanation: All strings are consistent.

Example 3:

Input: allowed = "cad", words = ["cc","acd","b","ba","bac","bad","ac","d"]
Output: 4
Explanation: Strings "cc", "acd", "ac", and "d" are consistent.

Constraints:
- 1 <= words.length <= 104
- 1 <= allowed.length <= 26
- 1 <= words[i].length <= 10
- The characters in allowed are distinct.
- words[i] and allowed contain only lowercase English letters.
See problem on LeetCode.

Solution: Set difference

Take the set difference between the words in words and allowed.
If there is no difference, increment the count.
Note that x.difference(y) returns a set that contains the items that only exist in set x (i.e., are unique to x), and don’t exist in set y.

class Solution:
    def countConsistentStrings(self, allowed: str, words: List[str]) -> int:
        count = 0
        
        for i in words:
            if not set(i).difference(set(allowed)):
                count += 1
                
        return count

Complexity

Time: $O(n)$
Space: $O(n)$

Pattern: Dictionary/Hash Table/Set

[12/Medium] Integer to Roman

Problem

Solution: Dictionary

Complexity

[13/Easy] Roman to Integer

Problem

Solution: Reverse the numeral, check if previous symbol is >= than the current one

Complexity

[146/Medium] LRU Cache

Problem

Solution: Deque

Solution: Deque + Dictionary

Solution: OrderedDict

Complexity

[208/Medium] Implement Trie (Prefix Tree)

Problem

Solution: Dictionary without a TrieNode class

Complexity

Solution: Using a TrieNode class implemented using a dict/defaultdict

Complexity

[246/Medium] Strobogrammatic Number

Problem

Solution: Set

Complexity

[249/Medium] Group Shifted Strings

Problem

Solution: Dictionary

Complexity

[266/Easy] Palindrome Permutation

Problem

Solution: Set

Complexity

Solution: Counter

Complexity

Solution: Counter one-liner

Complexity

[273/Hard] Integer to English Words

Problem

Solution: Brute force with Dictionary

Complexity

[290/Easy] Word Pattern

Solution: Use a pattern dictionary to track pattern

Complexity

[311/Medium] Sparse Matrix Multiplication

Problem

Solution: Use an if-condition to run the third loop only when we have a non-zero element

Complexity

Solution: Store non-zero elements in nested dictionaries and check those while calculating answer

Complexity

Solution: Two dictionaries

Complexity

[325/Medium] Maximum Size Subarray Sum Equals k

Problem

Solution: Dictionary

Complexity

[336/Hard] Palindrome Pairs

Problem

Solution: Trie

Complexity:

Solution: check each word for prefixes (and suffixes) that are themselves palindromes

Complexity

[340/Medium] Longest Substring with At Most K Distinct Characters

Problem

Solution: Two pointers + Hashmap

Complexity

[348/Medium] Design Tic-Tac-Toe

Problem

Solution: Counter to track each row, column and both diag counts for each player

Complexity

Solution: Four loops, one for each of row, col, diag and anti-diag

Complexity

Solution: Use a list/hash table to record the occurrence for each rows, cols and two diagonals

Complexity

[380/Medium] Insert Delete GetRandom O(1)

Problem

Solution: Dictionary

Complexity

[381/Medium] Insert Delete GetRandom O(1) - Duplicates allowed

Problem

Solution: `OrderedDict`

Solution: Dictionary without a `TrieNode` class

Solution: Using a `TrieNode` class implemented using a dict/`defaultdict`

Solution: `defaultdict` + `OrderedDict` + Binary Search

Solution: Find unique characters in `t`