Distilled • LeetCode • Graphs

• Pattern: Graphs
  • [797/Medium] All Paths From Source to Target
    • Problem
    • Solution: DFS
    • Solution: Recursive One-liner
      • Complexity
  • [997/Easy] Find the Town Judge
    • Problem
    • Solution: Maintain a score for each person to be a town judge candidate; add/subtract one if the person is trusted/trusts; check for count
      • Complexity
  • [1791/Easy] Find Center of Star Graph
    • Problem
    • Solution: Check the first two edges and return the overlapping node
      • Complexity
    • Solution: Generalized version: find multiple centers in a multi-star graph
      • Complexity
  • [1971/Easy] Find if Path Exists in Graph
    • Problem
    • Solution: DFS
      • Complexity

Pattern: Graphs

[797/Medium] All Paths From Source to Target

Problem

• Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

• The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

• Example 1:

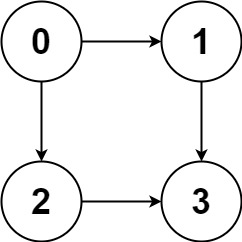
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

• Example 2:

Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

• Constraints:
  • n == graph.length
  • 2 <= n <= 15
  • 0 <= graph[i][j] < n
  • graph[i][j] != i (i.e., there will be no self-loops).
  • All the elements of graph[i] are unique.
  • The input graph is guaranteed to be a DAG.
• See problem on LeetCode.

Solution: DFS

• If it asks for just the number of paths, we can generally solve it in two ways:
  • Count from start to target in topological order.
  • Count using DFS with memo.
• Note that both of them have time \(O(Edges)\) and space \(O(Nodes)\).
• This problem asks for all paths. Memo might not save much time.
• Imagine the worst case that we have \(node-1\) to \(node-N\), and \(node-i\) linked to \(node-j\) if \(i < j\).
• There are \(2^(N-2)\) paths and \((N+2)*2^(N-3)\) nodes in all paths. We can roughly say \(O(2^N)\).

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        def dfs(cur, path):
            if cur == len(graph) - 1: 
                res.append(path)
            else:
                for i in graph[cur]: 
                    dfs(i, path + [i])
                    
        res = []
        dfs(0, [0])
        return res

Solution: Recursive One-liner

class Solution:
    def allPathsSourceTarget(self, g, cur=0):
        if cur == len(g) - 1: 
            return [[len(g) - 1]]
        
        return [([cur] + path) for i in g[cur] for path in self.allPathsSourceTarget(g, i)]

Complexity

• Time: \(O(n)\)
• Space: \(O(1)\)

[997/Easy] Find the Town Judge

Problem

• In a town, there are n people labeled from 1 to n. There is a rumor that one of these people is secretly the town judge.

• If the town judge exists, then:

  • The town judge trusts nobody.
  • Everybody (except for the town judge) trusts the town judge.
  • There is exactly one person that satisfies properties 1 and 2.

• You are given an array trust where trust[i] = [a_i, b_i] representing that the person labeled a_i trusts the person labeled bi.

• Return the label of the town judge if the town judge exists and can be identified, or return -1 otherwise.

• Example 1:

Input: n = 2, trust = [[1,2]]
Output: 2

• Example 2:

Input: n = 3, trust = [[1,3],[2,3]]
Output: 3

• Example 3:

Input: n = 3, trust = [[1,3],[2,3],[3,1]]
Output: -1

• Constraints:
  • 1 <= n <= 1000
  • 0 <= trust.length <= 104
  • trust[i].length == 2
  • All the pairs of trust are unique.
  • a_i != b_i
  • 1 <= a_i, b_i <= n
• See problem on LeetCode.

Solution: Maintain a score for each person to be a town judge candidate; add/subtract one if the person is trusted/trusts; check for count

from collections import Counter

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        # base case: early termination
        if n == 1 and trust == []:
            return 1
            
        # score for each person to be a town judge candidate
        score = Counter()
        
        # if a person trusts another person, decrease their score by one
        # (since the town judge trusts nobody)
        # if a person is trusted, increase their score by one
        # (since everybody trusts the town judge)
        for a, b in trust:
            score[a] -= 1
            score[b] += 1
        
        # count number of people which trust the candidates
        # if n-1 people trust one candidate it is the town judge
        for i in range(1, n + 1):
            if score[i] == n - 1:
                return i
                
        return -1

Complexity

• Time: \(O(n)\)
• Space: \(O(1)\)

[1791/Easy] Find Center of Star Graph

Problem

• There is an undirected star graph consisting of n nodes labeled from 1 to n. A star graph is a graph where there is one center node and exactly n - 1 edges that connect the center node with every other node.

• You are given a 2D integer array edges where each edges[i] = [u_i, v_i] indicates that there is an edge between the nodes u_i and v_i. Return the center of the given star graph.

• Example 1:

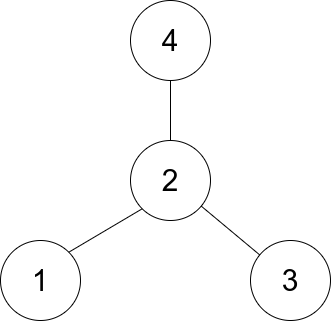
Input: edges = [[1,2],[2,3],[4,2]]
Output: 2
Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.

• Example 2:

Input: edges = [[1,2],[5,1],[1,3],[1,4]]
Output: 1

• Constraints:
  • 3 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 1 <= ui, vi <= n
  • ui != vi
  • The given edges represent a valid star graph.
• See problem on LeetCode.

Solution: Check the first two edges and return the overlapping node

• The solution is based on the following points:
  • The center is the only node that has more than one edge.
  • The center is also connected to all other nodes.
  • Any two edges must have a common node, which is the center.
• We can only check the first two edges and return the common node:

class Solution:
    def findCenter(self, edges: List[List[int]]) -> int:
        for i in edges[0]:
            if i in edges[1]:
                return i

class Solution:
    def findCenter(self, edges: List[List[int]]) -> int:
        return edges[0][0] if edges[0][0] == edges[1][0] or edges[0][0] == edges[1][1] else edges[0][1]

Complexity

• Time: \(O(1)\)
• Space: \(O(1)\)

Solution: Generalized version: find multiple centers in a multi-star graph

class Solution(object):
    def findCenter(self, edges):
        """
        :type edges: List[List[int]]
        :rtype: int
        """
        n = max(max(my_list) for my_list in edges)
        adj_list = [[] for _ in range(n)]
        
        for edge in edges:
            adj_list[edge[0]-1].append(edge[1]-1)
            adj_list[edge[1]-1].append(edge[0]-1)
            
        for i in range(len(adj_list)):
            if len(adj_list[i]) == n-1:
                return i +1

Complexity

• Time: \(O(n)\)
• Space: \(O(1)\)

[1971/Easy] Find if Path Exists in Graph

Problem

• There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [u_i, v_i] denotes a bi-directional edge between vertex u_i and vertex v_i. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

• You want to determine if there is a valid path that exists from vertex source to vertex destination.

• Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

• Example 1:

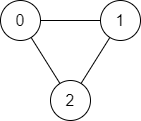
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

• Example 2:

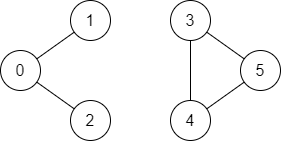
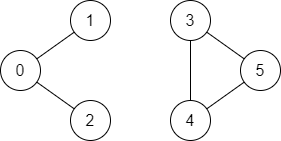
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

• Constraints:
  • 1 <= n <= 2 * 105
  • 0 <= edges.length <= 2 * 105
  • edges[i].length == 2
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 0 <= source, destination <= n - 1
  • There are no duplicate edges.
  • There are no self edges.
• See problem on LeetCode.

Solution: DFS

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        graph = self.makeGraph(edges)
        return self.depthFirstSearch(graph, source, destination, set())
    
    # format: {x: [y], y: [x]}
    def makeGraph(self,edges):
        graph = {}
        
        for edge in edges:
            x,y = edge
            
            if x not in graph:
                graph[x] = []
            if y not in graph:
                graph[y] = []
            
            graph[x].append(y)
            graph[y].append(x)
        return graph

    def depthFirstSearch(self, graph, node, target, visited):
        # base case: reached target
        if node == target:
            return True
        
        # mark visited nodes
        visited.add(node)
        
        for node in graph[node]:
            # don't want to visit a visited node
            if node not in visited:
                if self.depthFirstSearch(graph, node, target, visited):
                    return True
        
        return False

Complexity

• Time: \(O(n)\)
• Space: \(O(2n + n + n) = O(n)\)