Introduction

  • Dynamic Programming (DP) is a powerful technique used for solving a particular class of problems. The concept is based on a very simple overarching idea:

If you have solved a problem with a particular input, save the result for future reference, so as to avoid solving the same problem again!

Always remember:

“Those who can’t remember the past are condemned to repeat it!”

Two Ways of Solving DP Problems

  • Top-Down : Start solving the given problem by breaking it down. If you see that the problem has been solved already, then just return the saved answer. If it has not been solved, solve it and save the answer. This is referred to as memoization. Depending on the problem, the recursive method of DP is usually easy to think of and more intuitive than the bottom-up method.

The top-down paradigm of solving DP problems involves splitting the given problem repeatedly and ultimately working towards solving the base cases.

  • Bottom-Up : Analyze the problem and see the order in which the sub-problems are solved and start solving from the trivial sub-problem, up towards the given problem. In this process, it is guaranteed that the sub-problems are solved before solving the problem. This is referred to as dynamic programming.

The bottom-up paradigm of solving DP problems involves building up the solution by solving the base cases and working towards the given problem.

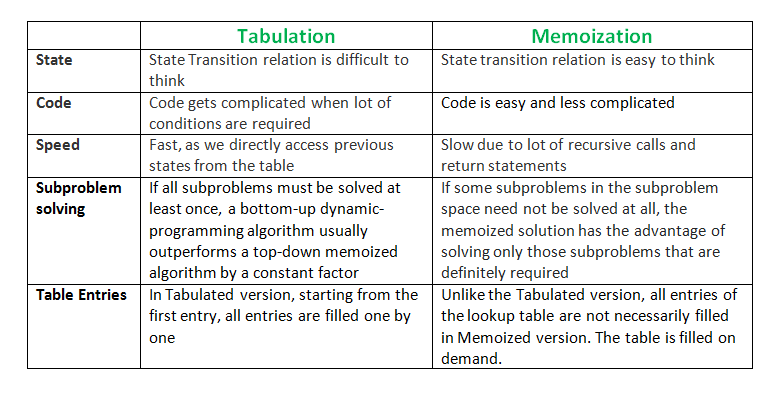
Tabulation vs. Memoization

  • As highlighted above, there are two different ways to store the values so that the values of a sub-problem can be reused. Here, will discuss two patterns of solving dynamic programming (DP) problems:

    1. Tabulation: Bottom-Up
    2. Memoization: Top-Down
  • Before getting to the definitions of the above two terms consider the following statements:
    • Version 1: Study the theory of DP, then practice some problems on classic DP, and ultimately master DP.
    • Version 2: To master DP, practice DP problems to realize the concepts of DP.
  • Both versions say the same thing, the difference simply lies in the way of conveying the message and that’s exactly how Bottom-Up and Top-Down DP differs. Version 1 can be associated with Bottom-Up DP and Version 2 can be associated with Top-Down DP.

Tabulation Method – Bottom Up Dynamic Programming

  • As the name itself suggests starting from the bottom and accumulating answers while working your way to the top. Let’s discuss in terms of state transitions.
  • Let’s define our DP problem to be finding dp[x], where dp[x = 0] is the base state and dp[x = n] is our destination state. In other words, the goal here is to find the value of the destination state, i.e., dp[n] using .
  • If we begin our series of transitions from the base state, i.e., dp[0] and follow our state transitions to reach our destination state dp[n], we call it the Bottom-Up approach, as reflected in it’s name – we started our series of transitions from the bottom-most base state and reached the top-most desired state.
  • Why do we call it the tabulation method? To know this let’s first look at some code to calculate the factorial of a number using a bottom-up approach. Once again, as our general procedure to solve a DP problem, we start by defining a state. In this case, we define a state as dp[x], where dp[x] is the factorial of x.
  • Per the definition of factorial, \(n! = n \times (n-1)!\). In terms of the aforementioned states, dp[x+1] = dp[x] * (x+1) or dp[x] = dp[x-1] * x
# Tabulated/bottom-up version to find the factorial of x.
dp = [0] * (n+1)

# base case
dp[0] = 1 # since 0! = 1

for i in range(1, n):
    dp[i] = dp[i-1] * i
  • The above code clearly follows the bottom-up approach as it starts its transition from the bottom-most base case dp[0] and reaches its destination state dp[n]. Here, we may notice that the DP table is being populated sequentially and we are directly accessing the calculated states from the table itself and hence, we call it the tabulation method (since the process is akin to sequentially entering rows of entries holding the results within a table and accessing them in future iterations).

Memoization Method – Top-Down Dynamic Programming

  • Similar to the bottom-up DP method above, let’s describe the process of solving DP problems in terms of state transitions. If we need to find the value for a state, say dp[n], instead of starting from the base state, i.e., dp[0], we seek our answer from states that arise as a result of splitting the state dp[n] into sub-problems following the state transition relation – which is the gist of the top-down pattern of DP.
  • Here, we start our journey from the top-most destination state and compute its answer by utilizing states that can help reach the destination state, till we reach the bottom-most base state.
  • Here’s some code for the factorial problem following the top-down DP pattern:
# Memoized version to find the factorial of x.
# To speed up, we store the values of calculated states.

# initialized to -1 to signify untouched states
dp = [0] * (n+1)

# return factorial of x!
def solve(x):
    # if x is <= 0
    if not x:
        return 1
        
    # if the result is pre-computed, 
    # return it as-is
    if dp[x] != -1
        return dp[x]
    
    # else compute dp[x] recursively
    dp[x] = x * solve(x-1)
    
    return dp[x]
  • As seen in the code snipped above, we are storing our answers in a DP cache so that if next time we’re looking to figure out the answer corresponding to this state, we can simply return it from memory. This is basically why we call this mode of solving DP problems “memoization”, since we are storing the results from processed states.
  • In this case, since the memory layout is linear, it may seem that the memory is being filled in a sequential manner (similar to the tabulation method), but you may consider other top-down DPs having a 2D memory layout such as Min Cost Path, where the memory is not filled in a sequential manner.

Advantages

  • Memoization is an optimization technique that is especially useful when it comes to dynamic programming which makes applications more efficient and hence faster. It does this by storing computation results in cache, and retrieving that same information from the cache the next time it’s needed instead of computing it again. A memoized function is usually faster because if the function is called subsequently with the previous value(s), then instead of executing the function, it would simply be fetching the result from the cache.

Comparison table

Example: Length of the Longest Increasing Subsequence

  • Given a sequence, the goal of the longest increasing subsequence problem is, as the name suggests, to find the longest increasing subsequence. Formally, given a sequence \(S={a_1, a_2, a_3, a_4, \ldots, a_{n-1}, a_n}\) we have to find a longest subset such that for all \(i\) and \(j\), \(j < i\) in the subset \(a_j < a_i\).
  • We start off by trying to find the value of the longest subsequence at every index \(i\), say \(LS_i\), with the last element of sequence being \(a_i\). As such, the largest \(LS_i\) would be the longest subsequence in the given sequence. To begin \(LSi\) is assigned to be one since \(a_i\) is element of the sequence (last element). Then for all \(j\) such that \(j < i\) and \(a_j < a_i\), we find the largest \(LS_j\) and add it to \(LSi\).
  • The algorithm is quadratic in time. In other words, it has a time complexity of \(O(n^2)\)

Pseudo-code

  • The time complexity of the algorithm can be reduced by using better a data structure rather than an array. Storing the predecessor array and its index would make the algorithm efficient.

  • A similar concept could be applied in finding longest path in Directed Acyclic Graph (DAG).

for i=0 to n-1
    LS[i]=1
    for j=0 to i-1
        if (a[i] > a[j] and LS[i] < LS[j])
            LS[i] = LS[j] + 1
for i=0 to n-1
    if (largest < LS[i])

Pattern: Dynamic Programming

[10/Hard] Regular Expression Matching

Problem

  • Given an input string s and a pattern p, implement regular expression matching with support for . and * where:
    • . Matches any single character.
    • * Matches zero or more of the preceding element.

  • The matching should cover the entire input string (not partial).

  • Example 1:
Input: s = "aa", p = "a"
Output: false
Explanation: "a" does not match the entire string "aa".
  • Example 2:
Input: s = "aa", p = "a*"
Output: true
Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa".
  • Example 3:
Input: s = "ab", p = ".*"
Output: true
Explanation: ".*" means "zero or more (*) of any character (.)".
  • Constraints:
    • 1 <= s.length <= 20
    • 1 <= p.length <= 30
    • s contains only lowercase English letters.
    • p contains only lowercase English letters, '.', and '*'.
    • It is guaranteed for each appearance of the character '*', there will be a previous valid character to match.
  • See problem on LeetCode.
Solution: DP
  • The following solution uses the in-place OR operator (|=) in Python, implemented using the __ior__() magic (check [here] or here for more info):
class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        # Initialize DP table
        # Row indices represent the lengths of subpatterns
        # Col indices represent the lengths of substrings
        dp = [
            [False for _ in range(len(s)+1)]
            for _ in range(len(p)+1)
        ]

        # Mark the origin as True, since p[:0] == "" and s[:0] == ""
        dp[0][0] = True

        # Consider all subpatterns p[:i], i > 0 against empty string s[:0]
        for i in range(1, len(p)+1):
            # Subpattern matches "" only if it consists of "{a-z}*" pairs
            dp[i][0] = i > 1 and dp[i-2][0] and p[i-1] == '*'

        # Consider the empty pattern p[:0] against all substrings s[:j], j > 0
        # Since an empty pattern cannot match non-empty strings, cells remain False

        # Match the remaining subpatterns (p[:i], i > 0) with the remaining
        # substrings (s[:j], j > 0)
        for i in range(1, len(p)+1):
            for j in range(1, len(s)+1):

                # Case 1: Last char of subpattern p[i-1] is an alphabet or '.'
                if p[i-1] == s[j-1] or p[i-1] == '.':
                    dp[i][j] |= dp[i-1][j-1]

                # Case 2: Last char of subpattern p[i-1] is '*'
                elif p[i-1] == '*':

                    # Case 2a: Subpattern doesn't need '*' to match the substring

                    # If the subpattern without '*' matches the substring,
                    # the subpattern with '*' must still match
                    dp[i][j] |= dp[i-1][j]

                    # If the subpattern without '*' and its preceding alphabet
                    # matches the substring, then the subpattern with them
                    # must still match
                    dp[i][j] |= i > 1 and dp[i-2][j]

                    # Case 2b: Subpattern needs '*' to match the substring

                    # If the alphabet preceding '*' matches the last char of
                    # the substring, then '*' is used to extend the match for
                    # the substring without its last char
                    if i > 1 and p[i-2] == s[j-1] or p[i-2] == '.':
                        dp[i][j] |= dp[i][j-1]

        return dp[-1][-1]

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        s, p = ' '+ s, ' '+ p
        lenS, lenP = len(s), len(p)
        dp = [[0]*(lenP) for i in range(lenS)]
        dp[0][0] = 1

        for j in range(1, lenP):
            if p[j] == '*':
                dp[0][j] = dp[0][j-2]

        for i in range(1, lenS):
            for j in range(1, lenP):
                if p[j] in {s[i], '.'}:
                    dp[i][j] = dp[i-1][j-1]
                elif p[j] == "*":
                    dp[i][j] = dp[i][j-2] or int(dp[i-1][j] and p[j-1] in {s[i], '.'})

        return bool(dp[-1][-1])
Complexity
  • Time: \(O(m+n)\) where m are the number of unique elements in encoded1, and n are unique numbers in encoded2
  • Space: \(O(len(encoded1) + len(encoded2))\)

[53/Easy] Maximum Subarray

Problem

  • Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

  • A subarray is a contiguous part of an array.

  • Example 1:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
  • Example 2:
Input: nums = [1]
Output: 1
  • Example 3:
Input: nums = [5,4,-1,7,8]
Output: 23
  • Constraints:
    • 1 <= nums.length <= 105
    • -104 <= nums[i] <= 104

F- ollow up: If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

Solution: Optimized Brute Force

  • Intuition:
    • This algorithm doesn’t reliably run under the time limit here on LeetCode. We’ll still look briefly at it though, as in an interview scenario it would be a great start if you’re struggling to come up with a better approach.
    • Calculate the sum of all subarrays, and keep track of the best one. To actually generate all subarrays would take \(O(n^3)\) time, but with a little optimization, we can achieve brute force in \(O(n^2)\) time. The trick is to recognize that all of the subarrays starting at a particular value will share a common prefix.
  • Algorithm:
    • Initialize a variable maxSubarray = -infinity to keep track of the best subarray. We need to use negative infinity, not 0, because it is possible that there are only negative numbers in the array.
    • Use a for loop that considers each index of the array as a starting point.
    • For each starting point, create a variable currentSubarray = 0. Then, loop through the array from the starting index, adding each element to currentSubarray. Every time we add an element it represents a possible subarray - so continuously update maxSubarray to contain the maximum out of the currentSubarray and itself.
    • Return maxSubarray.
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        max_subarray = -math.inf
        
        for i in range(len(nums)):
            current_subarray = 0
            for j in range(i, len(nums)):
                current_subarray += nums[j]
                max_subarray = max(max_subarray, current_subarray)
        
        return max_subarray
Complexity
  • Time: \(O(n^2)\), where \(n\) is the length of nums. We use two nested for loops, with each loop iterating through nums.
  • Space: \(O(1)\) since no matter how big the input is, we are only ever using two variables: ans and currentSubarray.

Solution: Kadane’s Algorithm: Track both min and max/DP

  • Intuition:
    • Whenever you see a question that asks for the maximum or minimum of something, consider Dynamic Programming as a possibility. The difficult part of this problem is figuring out when a negative number is “worth” keeping in a subarray. This question in particular is a popular problem that can be solved using an algorithm called Kadane’s Algorithm. If you’re good at problem solving though, it’s quite likely you’ll be able to come up with the algorithm on your own. This algorithm also has a very greedy-like intuition behind it.
    • Let’s focus on one important part: where the optimal subarray begins. We’ll use the following example. 
        nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
    • We can see that the optimal subarray couldn’t possibly involve the first 3 values - the overall sum of those numbers would always subtract from the total. Therefore, the subarray either starts at the first 4, or somewhere further to the right.
    • What if we had this example though? 
        nums = [-2,1000000000,-3,4,-1,2,1,-5,4]
    • We need a general way to figure out when a part of the array is worth keeping.
    • As expected, any subarray whose sum is positive is worth keeping. Let’s start with an empty array, and iterate through the input, adding numbers to our array as we go along. Whenever the sum of the array is negative, we know the entire array is not worth keeping, so we’ll reset it back to an empty array.
    • However, we don’t actually need to build the subarray, we can just keep an integer variable current_subarray and add the values of each element there. When it becomes negative, we reset it to 0 (an empty array).
  • Algorithm:
    • Initialize 2 integer variables. Set both of them equal to the first value in the array.
      • currentSubarray will keep the running count of the current subarray we are focusing on.
      • maxSubarray will be our final return value. Continuously update it whenever we find a bigger subarray.
    • Iterate through the array, starting with the 2nd element (as we used the first element to initialize our variables). For each number, add it to the currentSubarray we are building. If currentSubarray becomes negative, we know it isn’t worth keeping, so throw it away. Remember to update maxSubarray every time we find a new maximum.
    • Return maxSubarray.
  • Implementation:
    • A clever way to update currentSubarray is using currentSubarray = max(num, currentSubarray + num). If currentSubarray is negative, then num > currentSubarray + num.
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        # Initialize our variables using the first element.
        current_subarray = max_subarray = nums[0]
        
        # Start with the 2nd element since we already used the first one.
        for num in nums[1:]:
            # If current_subarray is negative, throw it away. Otherwise, keep adding to it.
            current_subarray = max(num, current_subarray + num)
            max_subarray = max(max_subarray, current_subarray)
        
        return max_subarray
Complexity
  • Time: \(O(n)\) where \(n\) is the size of nums. The algorithm achieves linear runtime since we are going through nums only once.
  • Space: \(O(1)\) since no matter how long the input is, we are only ever using two variables: currentSubarray and maxSubarray.

[70/Easy] Climbing Stairs

Problem

  • You are climbing a staircase. It takes n steps to reach the top.

  • Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

  • Example 1:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
  • Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
  • Constraints:
    • 1 <= n <= 45
  • See problem on LeetCode.
Solution: Bottom-up/Iterative DP
class Solution:
    def climbStairs(self, n: int) -> int:
        # edge cases
        if n == 0: return 0
        if n == 1: return 1
        if n == 2: return 2
                                      
        stairs = [0] * (n + 1)
        # consider 1st and 2nd step
        stairs[1] = 1
        stairs[2] = 2
        
        # start iteration from 3rd index        
        for i in range(3, n + 1):
            stairs[i] = stairs[i - 1] + stairs[i - 2]
        
        return stairs[n]
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

[139/Medium] Word Break

Problem

  • Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.

  • Note that the same word in the dictionary may be reused multiple times in the segmentation.

  • Example 1:

Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".
  • Example 2:
Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.
  • Example 3:
Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: false
  • Constraints:
    • 1 <= s.length <= 300
    • 1 <= wordDict.length <= 1000
    • 1 <= wordDict[i].length <= 20
    • s and wordDict[i] consist of only lowercase English letters.
    • All the strings of wordDict are unique.
  • See problem on LeetCode.

Solution: Brute Force

  • The naive approach to solve this problem is to use recursion and backtracking. For finding the solution, we check every possible prefix of that string in the dictionary of words, if it is found in the dictionary, then the recursive function is called for the remaining portion of that string. And, if in some function call it is found that the complete string is in dictionary, then it will return true.
class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        def wordBreakRecur(s: str, word_dict: Set[str], start: int):
            if start == len(s):
                return True
   
            for end in range(start + 1, len(s) + 1):
                if s[start:end] in word_dict and wordBreakRecur(s, word_dict, end):
                    return True
   
            return False

        return wordBreakRecur(s, set(wordDict), 0)
Complexity
  • Time: \(O(2^n)\). Given a string of length \(n\), there are \(n + 1\) ways to split it into two parts. At each step, we have a choice: to split or not to split. In the worse case, when all choices are to be checked, that results in \(O(2^n)\).
  • Space: \(O(n)\). The depth of the recursion tree can go upto \(n\).

Solution: Recursion with memoization

  • In the previous approach we can see that many subproblems were redundant, i.e., we were calling the recursive function multiple times for a particular string. To avoid this we can use memoization method, where an array is used to store the result of the subproblems. Now, when the function is called again for a particular string, value will be fetched and returned using the array, if its value has been already evaluated.
  • With memoization many redundant subproblems are avoided and recursion tree is pruned and thus it reduces the time complexity by a large factor.
class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        @lru_cache
        def wordBreakMemo(s: str, word_dict: FrozenSet[str], start: int):
            if start == len(s):
                return True
                
            for end in range(start + 1, len(s) + 1):
                if s[start:end] in word_dict and wordBreakMemo(s, word_dict, end):
                    return True
            return False

        return wordBreakMemo(s, frozenset(wordDict), 0)

Complexity

  • Time: \(O(n^3)\). \(n\) for the for loop. \(n\) for the substring. And \(n\) for recursion tree.
  • Space: \(O(n)\). The depth of recursion tree can go up to \(n\).
  • Another approach is to use Breadth-First-Search. Visualize the string as a tree where each node represents the prefix upto index \(end\). Two nodes are connected only if the substring between the indices linked with those nodes is also a valid string which is present in the dictionary. In order to form such a tree, we start with the first character of the given string (say \(s\)) which acts as the root of the tree being formed and find every possible substring starting with that character which is a part of the dictionary.
  • Further, the ending index (say \(i\)) of every such substring is pushed at the back of a queue which will be used for Breadth First Search. Now, we pop an element out from the front of the queue and perform the same process considering the string \(s(i+1,end)\) to be the original string and the popped node as the root of the tree this time. This process is continued, for all the nodes appended in the queue during the course of the process. If we are able to obtain the last element of the given string as a node (leaf) of the tree, this implies that the given string can be partitioned into substrings which are all a part of the given dictionary.
class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        word_set = set(wordDict)
        q = deque()
        visited = set()

        q.append(0)
        
        while q:
            start = q.popleft()
            if start in visited:
                continue
                
            for end in range(start + 1, len(s) + 1):
                if s[start:end] in word_set:
                    q.append(end)
                    if end == len(s):
                        return True
            visited.add(start)
            
        return False

Complexity

  • Time: \(O(n^3)\). \(n\) for the while loop. \(n\) for the for loop. \(n\) for the substring. Note that for every starting index, the search can continue till the end of the given string.
  • Space: \(O(n)\)

Solution: Dynamic Programming

  • The intuition behind this approach is that the given problem (\(s\)) can be divided into subproblems \(s1\) and \(s2\). If these subproblems individually satisfy the required conditions, the complete problem, ss also satisfies the same. e.g. “catsanddog” can be split into two substrings “catsand”, “dog”. The subproblem “catsand” can be further divided into “cats”,”and”, which individually are a part of the dictionary making “catsand” satisfy the condition. Going further backwards, “catsand”, “dog” also satisfy the required criteria individually leading to the complete string “catsanddog” also to satisfy the criteria.
  • Now, we’ll move onto the process of dp array formation. We make use of dp array of size \(n+1\), where \(n\) is the length of the given string. We also use two index pointers \(i\) and \(j\), where \(i\) refers to the length of the substring \(\left(s^{\prime}\right)\) considered currently starting from the beginning, and \(j\) refers to the index partitioning the current substring \(\left(s^{\prime}\right)\) into smaller substrings \(s^{\prime}(0, j)\) and \(s^{\prime}(j+1, i)\). To fill in the dp array, we initialize the element \(\mathrm{dp}[0]\) as true, since the null string is always present in the dictionary, and the rest of the elements of dp as false. We consider substrings of all possible lengths starting from the beginning by making use of index \(i\). For every such substring, we partition the string into two further substrings \(s 1^{\prime}\) and \(s 2^{\prime}\) in all possible ways using the index \(j\) (Note that the \(i\) now refers to the ending index of \(s 2^{\prime}\) ). Now, to fill in the entry \(\mathrm{dp}[i]\), we check if the \(\operatorname{dp}[j]\) contains true, i.e. if the substring \(s 1^{\prime}\) fulfills the required criteria. If so, we further check if \(s 2^{\prime}\) is present in the dictionary. If both the strings fulfill the criteria, we make \(dp[i]\) as true, otherwise as false.
class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:

        dp = [False] * (len(s)+1)
        dp[0] = True
        
        for i in range(1, len(s)+1):
            for j in range(i):
                if dp[j] and s[j:i] in wordDict:
                    dp[i] = True
                    break
        
        return dp[-1] # or dp[len(s)]

Complexity

  • Time: \(O(n^3)\). There are two nested loops, and substring computation at each iteration. Overall that results in \(O(n^3)\) time complexity.
  • Space: \(O(n)\). Length of \(p\) array is \(n+1\).

[152/Medium] Maximum Product Subarray

Problem

  • Given an integer array nums, find a contiguous non-empty subarray within the array that has the largest product, and return the product.

  • The test cases are generated so that the answer will fit in a 32-bit integer.

  • A subarray is a contiguous subsequence of the array.

  • Example 1:

Input: nums = [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.
  • Example 2:
Input: nums = [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.
  • Constraints:
    • 1 <= nums.length <= 2 * 104
    • -10 <= nums[i] <= 10
    • The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.
  • See problem on LeetCode.

Solution: Brute Force

  • Intuition:
    • The most naive way to tackle this problem is to go through each element in nums, and for each element, consider the product of every a contiguous subarray starting from that element. This will result in a cubic runtime. 
        for i in [0...nums-1]: 
      for j in [i..nums-1]: 
          accumulator = 1
          for k in [i..j]:
              accumulator = accumulator * nums[k]
          result = max(result, accumulator)
    • We can improve the runtime from cubic to quadratic by removing the innermost for loop in the above pseudo code. Rather than calculating the product of every contiguous subarray over and over again, for each element in nums (the outermost for loop), we accumulate the products of contiguous subarrays starting from that element to subsequent elements as we go through them (the second for loop). By doing so, we only need to multiply the current number with accumulated product to get the product of numbers up to the current number.

    Note: This brute force approach is included solely to build the foundation for understanding the following approach. This approach is not expected to pass all test cases.

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if len(nums) == 0:
            return 0

        result = nums[0]

        for i in range(len(nums)):
            accu = 1
            for j in range(i, len(nums)):
                accu *= nums[j]
                result = max(result, accu)

        return result
Complexity
  • Time: \(O(n^2)\) where \(n\) is the size of nums. Since we are checking every possible contiguous subarray following every element in nums we have quadratic runtime.
  • Space: \(O(1)\) since we are not consuming additional space other than two variables: result to hold the final result and accu to accumulate product of preceding contiguous subarrays.

Solution: Kadane’s Algorithm: Track both min and max/DP

  • Intuition:
    • The key intuition here is that when we can come upon a negative number, our current max can suddenly becomes a min but is still a max by absolute value. Following the next negative number, our min can become a max again. Therefore keeping track of min is useful.
  • Explanation:
    • Rather than looking for every possible subarray to get the largest product, we can scan the array and solve smaller subproblems.
    • Let’s see this problem as a problem of getting the highest combo chain. The way combo chains work is that they build on top of the previous combo chains that you have acquired. The simplest case is when the numbers in nums are all positive numbers. In that case, you would only need to keep on multiplying the accumulated result to get a bigger and bigger combo chain as you progress.
    • However, two things can disrupt your combo chain:
      • Zeros
      • Negative numbers
    • Zeros will reset your combo chain. A high score which you have achieved will be recorded in placeholder result. You will have to restart your combo chain after zero. If you encounter another combo chain which is higher than the recorded high score in result, you just need to update the result.
    • Negative numbers are a little bit tricky. A single negative number can flip the largest combo chain to a very small number. This may sound like your combo chain has been completely disrupted but if you encounter another negative number, your combo chain can be saved. Unlike zero, you still have a hope of saving your combo chain as long as you have another negative number in nums (Think of this second negative number as an antidote for the poison that you just consumed). However, if you encounter a zero while you are looking your another negative number to save your combo chain, you lose the hope of saving that combo chain.
    • While going through numbers in nums, we will have to keep track of the maximum product up to that number (we will call max_so_far) and minimum product up to that number (we will call min_so_far). The reason behind keeping track of max_so_far is to keep track of the accumulated product of positive numbers. The reason behind keeping track of min_so_far is to properly handle negative numbers.
    • max_so_far is updated by taking the maximum value among:
      1. Current number.
      • This value will be picked if the accumulated product has been really bad (even compared to the current number). This can happen when the current number has a preceding zero (e.g. [0,4]) or is preceded by a single negative number (e.g. [-3,5]). 1. Product of last max_so_far and current number.
      • This value will be picked if the accumulated product has been steadily increasing (all positive numbers). 1. Product of last min_so_far and current number.
      • This value will be picked if the current number is a negative number and the combo chain has been disrupted by a single negative number before (In a sense, this value is like an antidote to an already poisoned combo chain).
    • min_so_far is updated in using the same three numbers except that we are taking minimum among the above three numbers.
    • In the animation below, you will observe a negative number -5 disrupting a combo chain but that combo chain is later saved by another negative number -4. The only reason this can be saved is because of min_so_far. You will also observe a zero disrupting a combo chain.
class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if len(nums) == 0:
            return 0

        max_so_far = nums[0]
        min_so_far = nums[0]
        result = max_so_far

        for i in range(1, len(nums)):
            curr = nums[i]

            # have a temp because max gets calculated first and it will affect min's calculation
            temp_max = max(curr, max_so_far * curr, min_so_far * curr)
            min_so_far = min(curr, max_so_far * curr, min_so_far * curr)

            max_so_far = temp_max

            result = max(max_so_far, result)
        return result
  • Same approach; rehashed:
def maxProduct(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        prev_max = nums[0] # max from previous iteration
        prev_min = nums[0] # min from previous iteration
        max_to_n = nums[0] # max this iteration
        min_to_n = nums[0] # min this iteration
        ans = nums[0]
        
        for i in nums[1:]
            # use previous max/min*current i or restart from i. The absolute value of the min could be larger so we store it.
            max_to_n = max(max(prev_max*i, prev_min*i), i)
            min_to_n = min(min(prev_max*i, prev_min*i), i)
            prev_max = max_to_n
            prev_min = min_to_n
            ans = max(ans, max_to_n)
        return ans
Complexity
  • Time: \(O(n)\) where \(n\) is the size of nums. The algorithm achieves linear runtime since we are going through nums only once.
  • Space: \(O(1)\) since no additional space is consumed rather than variables which keep track of the maximum product so far, the minimum product so far, current variable, temp variable, and placeholder variable for the result.

[304/Medium] Range Sum Query 2D - Immutable

Problem

  • Given a 2D matrix matrix, handle multiple queries of the following type:

    • Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

  • Implement the NumMatrix class:

    • NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
    • int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

  • Example 1:

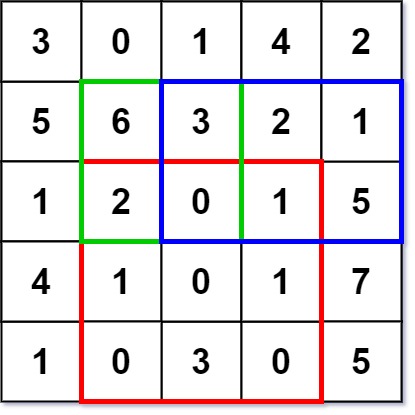
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
  • Constraints:
    • m == matrix.length
    • n == matrix[i].length
    • 1 <= m, n <= 200
    • -105 <= matrix[i][j] <= 105
    • 0 <= row1 <= row2 < m
    • 0 <= col1 <= col2 < n
  • See problem on LeetCode.

Solution: Precompute sums for all matrices with (0, 0) as top left corner and (i, j) as bottom right corner

  • Simple explanation:
    • The idea is simple, just precompute sums for all matrices with (0, 0) as top left corner and (i, j) as bottom right corner. There are \(O(n^2)\) of these matrices, so we store them in a 2D table. In order to make code simpler, we add an extra column and row, filled with 0.
  • Detailed explanation:
    • This problem brings up one of the characteristics of a 2D matrix: the sum of the elements in any rectangular range of a matrix (M) can be defined mathematically by the overlap of four other rectangular ranges that originate at matrix[0][0].
    • The sum of the rectangle (0,0)->(i,j) is equal to the cell (i,j), plus the rectangle (0,0)->(i,j-1), plus the rectangle (0,0)->(i-1,j), minus the rectangle (0,0)->(i-1,j-1). We subtract the last rectangle because it represents the overlap of the previous two rectangles that were added.

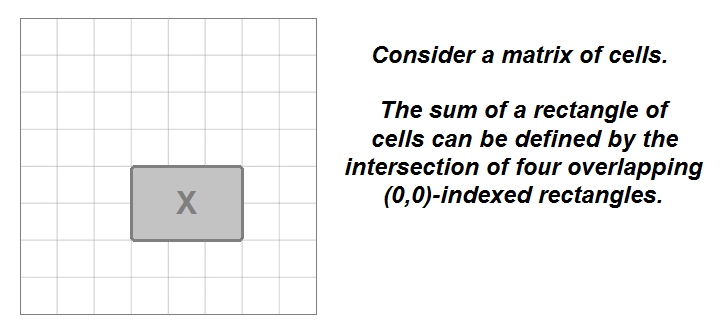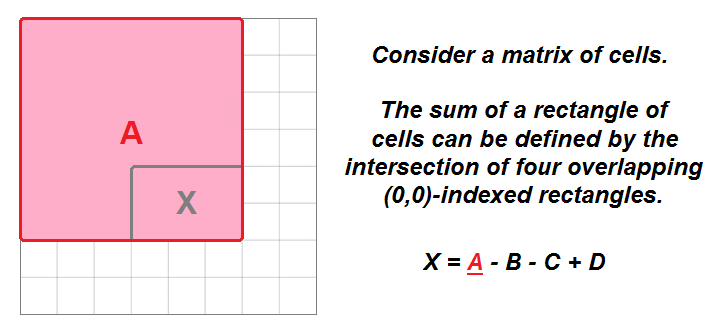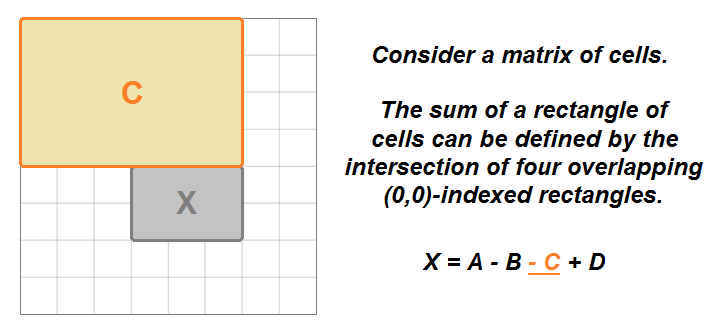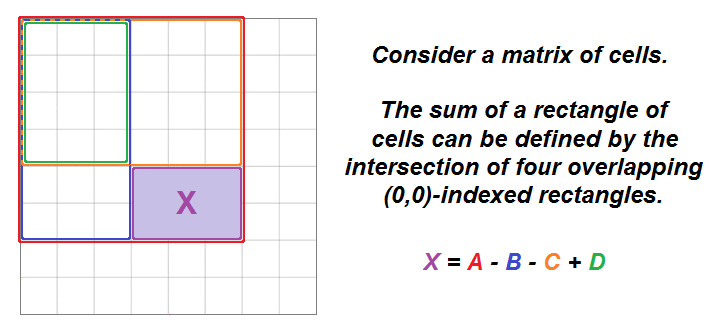
    • With this information, we can use a dynamic programming (DP) approach to build a prefix sum matrix (dp) from matrix iteratively, where dp[i][j] will represent the sum of the rectangle (0,0)->(i,j). We’ll add an extra row and column in order to prevent out-of-bounds issues at i-1 and j-1 (similar to a prefix sum array), and we’ll fill dp with 0s.
    • At each cell, we’ll add its value from matrix to the dp values of the cell on the left and the one above, which represent their respective rectangle sums, and then subtract from that the top-left diagonal value, which represents the overlapping rectangle of the previous two additions.
    • Then, we just reverse the process for sumRegion(): We start with the sum at dp[row2+1][col2+1] (due to the added row/column), then subtract the left and top rectangles before adding back in the doubly-subtracted top-left diagonal rectangle.
    • Note: Even though the test cases will pass when using an int matrix for dp, the values of dp can range from -4e9 to 4e9 per the listed constraints, so we should use a data type capable of handling more than 32 bits.
class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        if not matrix:
            return 
            
        ylen, xlen = len(matrix), len(matrix[0])
        self.dp = [[0 for _ in range(xlen+1)] for _ in range(ylen+1)] # or [[0] * (xlen+1) for _ in range(ylen+1)]
        for i in range(ylen):
            for j in range(xlen):
                self.dp[i+1][j+1] = matrix[i][j] + self.dp[i][j+1] + self.dp[i+1][j] - self.dp[i][j]
        # or 
        # for i in range(1, ylen):
        #    for j in range(1, xlen):
        #        self.dp[i][j] = dp[i-1][j-1] + self.dp[i-1][j] + self.dp[i][j-1] - self.dp[i-1][j-1]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.dp[row2+1][col2+1] - self.dp[row1][col2+1] - self.dp[row2+1][col1] + self.dp[row1][col1]
        
# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)
Complexity
  • Time:
    • constructor: \(O(m * n)\) where \(m\) and \(n\) are the dimensions of the input matrix
    • sumRegion: \(O(1)\)
  • Space:
    • constructor: \(O(m * n)\) for the DP matrix
    • constructor: \(O(1)\) if you’re able to modify the input and use an in-place DP approach
    • sumRegion: \(O(1)\)

[322/Medium] Coin Change

Problem

  • You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

  • Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

  • You may assume that you have an infinite number of each kind of coin.

  • Example 1:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1
  • Example 2:
Input: coins = [2], amount = 3
Output: -1
  • Example 3:
Input: coins = [1], amount = 0
Output: 0
  • Constraints:
    • 1 <= coins.length <= 12
    • 1 <= coins[i] <= 2^31 - 1
    • 0 <= amount <= 104
  • See problem on LeetCode.

Solution: Brute-Force

  • The problem could be modeled as the following optimization problem : \(\min_{x} \sum_{i=0}^{n - 1} x_i\) subject to \(\sum_{i=0}^{n - 1}\) , where \(a\) is the amount, \(c_i\) is the coin denominations, \(x_i\) is the number of coins with denominations \(c_i\) used in change of amount \(a\). We could easily see that \(x_i = [{0, \frac{a}{c_i}}]\)

  • A trivial solution is to enumerate all subsets of coin frequencies \([x_0\dots x_{n - 1}]\) that satisfy the constraints above, compute their sums and return the minimum among them.

  • Algorithm:
    • To apply this idea, the algorithm uses backtracking technique to generate all combinations of coin frequencies \([x_0\dots x_{n-1}]\) in the range \(([{0, \frac{a}{c_i}}])\) which satisfy the constraints above. It makes a sum of the combinations and returns their minimum or -1 in case there is no acceptable combination.

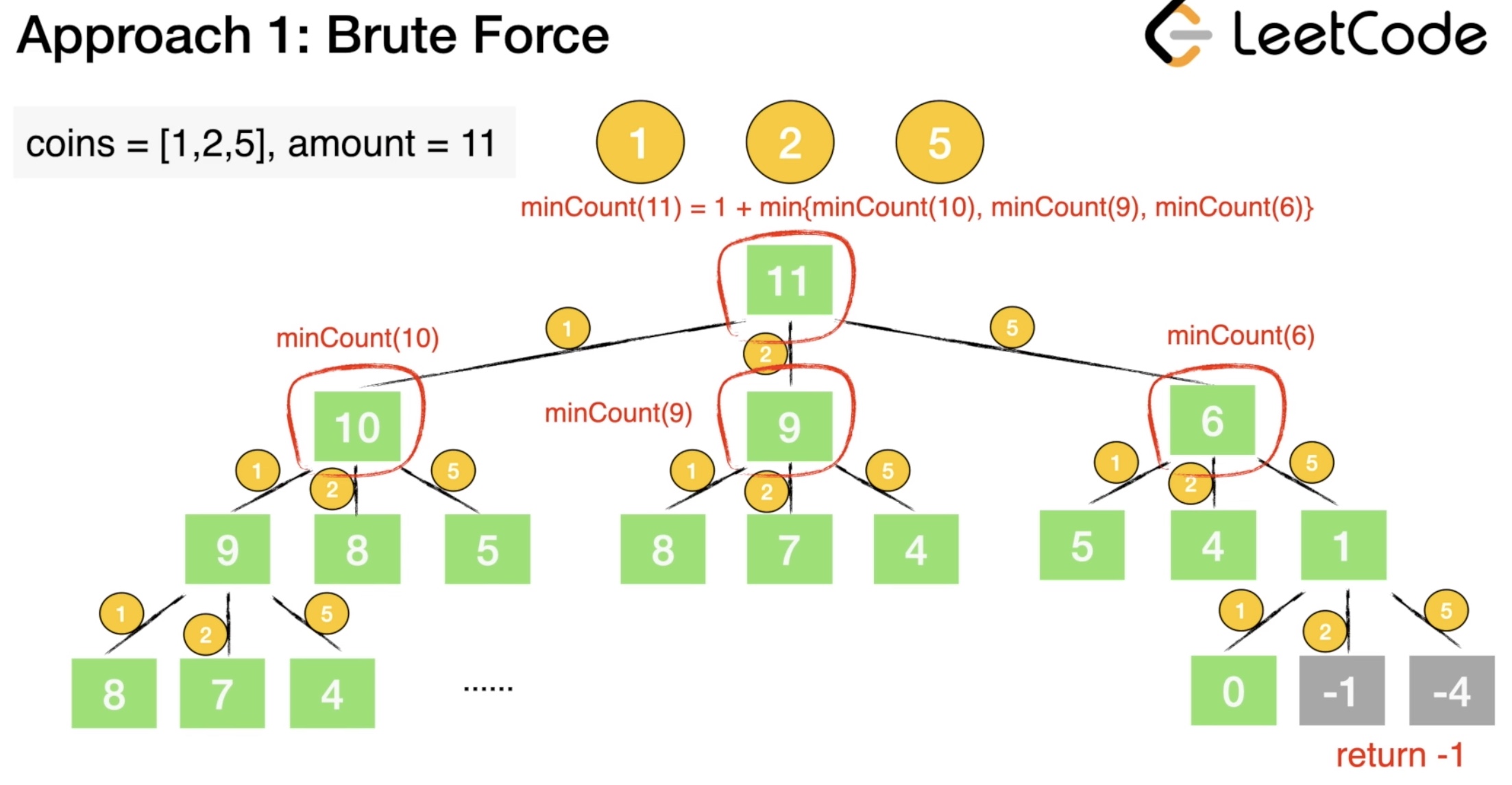
Complexity
  • Time: \(O(a^n)\). In the worst case, we would have \(a\) subproblems, where each subproblem can be solved in \(n\) ways.
  • Space: \(O(a)\). In the worst case, we would need to use coins of denomination 1 to make up the amount, making the depth of recursion \(a\). Therefore we need \(O(a)\) space used by the system recursive stack.

Solution: Top-down/Recursive DP

  • Intuition:
    • Could we improve the exponential solution above? Definitely! The problem could be solved with polynomial time using Dynamic Programming. First, let’s define:

    \(F(a)\) - minimum number of coins needed to make change for amount \(a\) using coin denominations \([{c_0\ldots c_{n-1}}]\)

    • We note that this problem has an optimal substructure property, which is the key piece in solving any Dynamic Programming problems. In other words, the optimal solution can be constructed from optimal solutions of its subproblems. How to split the problem into subproblems? Let’s assume that we know \(F(a)\) where some change val_1, val_2, … for \(a\) which is optimal and the last coin’s denomination is CC. Then the following equation should be true because of optimal substructure of the problem:
    \[F(a) = F(a - C) + 1\]
    • But we don’t know which is the denomination of the last coin \(C\). We compute \(F(a - c_i)\) for each possible denomination \(c_0, c_1, c_2 \ldots c_{n -1}\) and choose the minimum among them. The following recurrence relation holds:

    \(F(a) = \min_{i=0 ... n-1} { F(a - c_i) } + 1 \\ \text{subject to} \ a-c_i \geq 0\) - \(F(a)=0, \text{when} a=0 \\ F(a) = -1 , \text{when} n = 0\)

  • Recursion tree for finding coin change of amount 6 with coin denominations {1,2,3}:

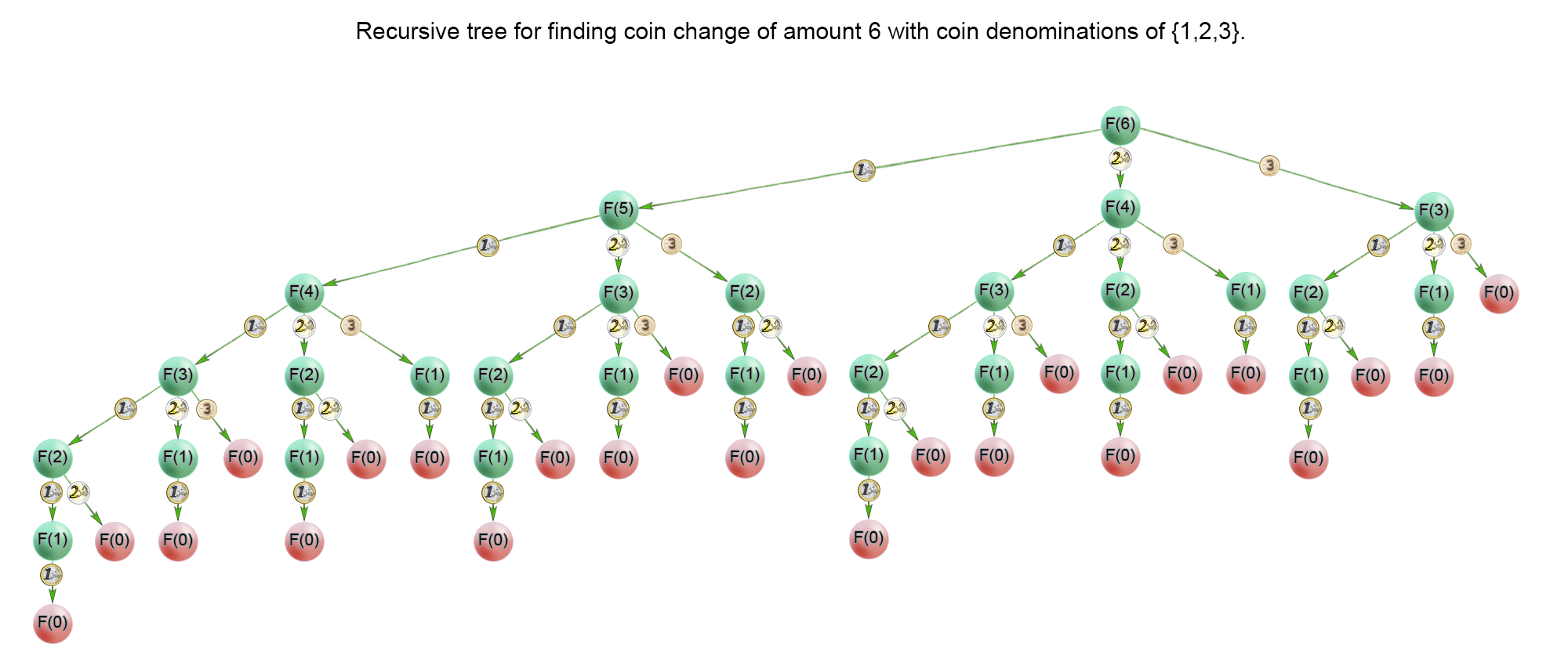
  • In the recursion tree above, we could see that a lot of subproblems were calculated multiple times. For example the problem \(F(1)\) was calculated 1313 times. Therefore we should cache the solutions to the subproblems in a table and access them in constant time when necessary.

  • Algorithm:

    • The idea of the algorithm is to build the solution of the problem from top to bottom. It applies the idea described above. It use backtracking and cut the partial solutions in the recursive tree, which doesn’t lead to a viable solution. Тhis happens when we try to make a change of a coin with a value greater than the amount \(a\). To improve time complexity we should store the solutions of the already calculated subproblems in a table.
Complexity
  • Time: \(O(a*n)\). where \(a\) is the amount, \(n\) is number of denominations available. In the worst case, the recursive tree of the algorithm has height of \(a\) and the algorithm solves only \(a\) subproblems because it caches precalculated solutions in a table. Each subproblem is computed with \(n\) iterations, each corresponding to one coin denomination. Therefore there is \(O(a*n)\) time complexity.
  • Space: \(O(a)\). We use extra space for the memoization table.

Solution: Bottom-up/Iterative DP

  • The problem could be solved with polynomial time using Dynamic Programming. First, let’s define:

    \(F(a)\) - minimum number of coins needed to make change for amount \(a\) using coin denominations \([{c_0\ldots c_{n-1}}]\)

  • We note that this problem has an optimal substructure property, which is the key piece in solving any Dynamic Programming problems. In other words, the optimal solution can be constructed from optimal solutions of its subproblems. How to split the problem into subproblems? Let’s assume that we know \(F(a)\) where some change val_1, val_2, … for \(a\) which is optimal and the last coin’s denomination is CC. Then the following equation should be true because of optimal substructure of the problem:

\[F(a) = F(a - C) + 1\]

  • But we don’t know which is the denomination of the last coin \(C\). We compute \(F(a - c_i)\) for each possible denomination \(c_0\), \(c_1\), \(c_2 \ldots c_{n -1}\) and choose the minimum among them.

  • Before calculating \(F(i)\), we have to compute all minimum counts for amounts up to \(i\). On each iteration \(i\) of the algorithm \(F(i)\) is computed as \(\min_{j=0 \ldots n-1}{F(i -c_j)} + 1\).

  • In the example above you can see that:
\[\begin{aligned} F(3) &= \min{(F(3- c_1), F(3-c_2), F(3-c_3))} + 1 \\ &= \min{(F(3- 1), F(3-2), F(3-3))} + 1 \\ &= \min{(F(2), F(1), F(0))} + 1 \\ &= \min{(1, 1, 0)} + 1 \\ &= 1 \end{aligned}\] 
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1) # or math.inf
        dp[0] = 0
        
        for coin in coins:
            # for each coin, go from the difference in value of the current coin to the amount 
            # and add the number of combinations for (index-coin)
            # note that the loop starts from the value of the coin because a coin does not impact 
            # any combination counts less than it's value. 
            # as shown above -- consider value=2, all amounts less than 2 are not impacted by the presence of 2 cent coins.            
            for x in range(coin, amount + 1):
                # the +1 below is because we've considered "coin", we need to add 1 to the number of coins 
                dp[x] = min(dp[x], dp[x-coin] + 1)
        
        return dp[amount] if dp[amount] != float('inf') else -1 # or math.inf
Complexity
  • Time: \(O(a*n)\). where \(a\) is the amount, \(n\) is number of denominations available. In the worst case, we have \(S\) subproblems. Each subproblem is computed with \(n\) iterations, each corresponding to one coin denomination. In other words, on each step the algorithm finds the next \(F(i)\) in \(n\) iterations, where \(1\leq i \leq S\). Therefore in total the iterations are \(S*n\).
  • Space: \(O(a)\). We use extra space for the memoization table.

[329/Hard] Longest Increasing Path in a Matrix

Problem

  • Given an m x n integers matrix, return the length of the longest increasing path in matrix.

  • From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

  • Example 1:

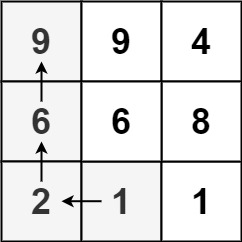
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].
  • Example 2:

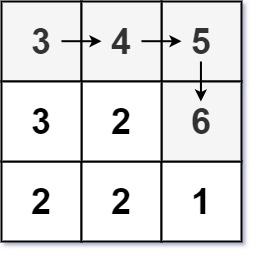
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.
  • Example 3:
Input: matrix = [[1]]
Output: 1
  • Constraints:
    • m == matrix.length
    • n == matrix[i].length
    • 1 <= m, n <= 200
    • 0 <= matrix[i][j] <= 2^31 - 1
  • See problem on LeetCode.

Solution: Topological Sort with BFS

  • Search around to find the # of incoming nodes.
  • Start with zero indegree with queue, pop from queue, search around and reduce the indegree by 1.
  • Push to queue if indegree is 0.
  • Output the steps.
class Solution:
    def longestIncreasingPath(self, matrix):
        if not matrix:
            return 0
            
        m, n = len(matrix), len(matrix[0])
        directions = [(1,0), (-1,0), (0,1), (0,-1)]
        hmap = {}
        
        queue = collections.deque()
        for i in range(m):
            for j in range(n):
                cnt = 0
                for dx, dy in directions:
                    x = i + dx
                    y = j + dy
                    if 0 <= x <= m-1 and 0 <= y <= n-1 and matrix[x][y] < matrix[i][j]:
                        cnt += 1
                        
                hmap[(i, j)] = cnt # map point to the # of incoming degree
                if cnt == 0:
                    queue.append((i, j)) # append point (i,j) to queue
                    
        # bfs with queue, and update the step until queue is empty
        step = 0
        while queue:
            size = len(queue)
            for k in range(size):
                i, j = queue.popleft()
                for dx, dy in directions:
                    x = i + dx
                    y = j + dy
                    if 0 <= x <= m-1 and 0 <= y <= n-1 and matrix[x][y] > matrix[i][j] and (x, y) in hmap:
                        hmap[(x, y)] -= 1
                        if hmap[(x, y)] == 0:
                            queue.append((x, y))
            step += 1
        return step
Complexity
  • Time: \(O(\midV\mid+\midE\mid)\)
  • Space: \(O(\midV\mid+\midE\mid)\)

Solution: Recursive/Top-down DP with DFS

  • Summary:
    • Take dp of each element in the matrix to show the maximum length of path that can be traveled from that element (source) to any other element (destination) keeping the path strictly increasing.
  • Solution:
    • The maximum value out of all the dp of elements will give us the longest increasing path possible.
  • Flow:
    • We can find longest decreasing path instead, the result will be the same. Initialize dp as -1 to show every element in matrix as unvisited (not calculated), recursively go through each element and keep on upsolving the dp by visiting neighbour elements (left, right, up, down) if possible (inside the matrix) and conditions satisfy (strictly increasing). Use dp to record previous results and choose the max dp value of smaller neighbors.
def longestIncreasingPath(matrix: [[int]]) -> int:
    def dfs(row: int, col: int) -> int:
        if dp[row][col] == -1:  # only calculate if not already done
            val = matrix[row][col]
            dfs_up = dfs(row - 1, col) if row and val < matrix[row - 1][col] else 0
            dfs_down = dfs(row + 1, col) if row + 1 < m and val < matrix[row + 1][col] else 0
            dfs_left = dfs(row, col - 1) if col and val < matrix[row][col - 1] else 0
            dfs_right = dfs(row, col + 1) if col + 1 < n and val < matrix[row][col + 1] else 0
            dp[row][col] = 1 + max(dfs_up, dfs_down, dfs_left, dfs_right)
        return dp[row][col]

    m, n = len(matrix), len(matrix[0])
    dp = [[-1] * n for _ in range(m)]
    return max(dfs(r, c) for r in range(m) for c in range(n))
  • Similar approach; rehashed:
class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        def dfs(i, j):
            if not dp[i][j]:
                val = matrix[i][j]
                dp[i][j] = 1 + max(
                    dfs(i - 1, j) if i and val > matrix[i - 1][j] else 0,
                    dfs(i + 1, j) if i < M - 1 and val > matrix[i + 1][j] else 0,
                    dfs(i, j - 1) if j and val > matrix[i][j - 1] else 0,
                    dfs(i, j + 1) if j < N - 1 and val > matrix[i][j + 1] else 0)
            return dp[i][j]

        if not matrix or not matrix[0]: return 0
        M, N = len(matrix), len(matrix[0])
        dp = [[0] * N for i in range(M)]
        
        return max(dfs(x, y) for x in range(M) for y in range(N))
Complexity
  • Time: \(O(mn)\) since we check the items of matrix just only one.
    • This looks like a graph problem. If we define $G=(V, E)$, where:
    • \(V=v_{i j}\) for \(0 \leq i<\mid\) matrix \(\mid\) and \(0 \leq j<\mid\) matrix \([i] \mid\)
    • \(E=(u, v)\) for \(u \epsilon V, v \epsilon\) neighbor \(s(u) \epsilon V\) and \(\operatorname{val}(u)<\operatorname{val}(v)\)
    • Now we need to find the longest path in the directed graph.
    • We can do a DFS from each vertex and track the max path length. DFS is \(O(V+E)\), but we have at most 4 edges per vertex in this graph, so this DFS is \(O(V)\). since we do it \(V\) times, the runtime is \(O\left(V^{2}\right)\). With caching, the DFS only has to touch each vertex once, so the total runtime is \(O(V)=O(m n)\).
  • Space: \(O(mn)\) for dp

Solution: Recursive/Top-down DP with DFS and Memoization

  • Using lru_cache:

    • The naive approach here would be to iterate through the entire matrix (M) and attempt to traverse down each branching path, but we’d find ourselves repeating the same stretches of path over and over again.

    • Rather than having to repeat sub-problems, we should cache those completed sub-problem results for future use in a memoization data structure. Since the paths can branch at any location, we should also use a depth-first search (DFS) approach with recursion to efficiently traverse the paths. Python’s @lru_cache offers great in-built memoization instead of having to manually create a memoization data structure. It enables us to record previous results to smaller sub-problems and we simply choose the max value among all four directions.

    • Note that it is possible to use a bottom-up dynamic programming (DP) approach here as well, but since there’s no convenient fixed point bottom location, we’d have to use a max-heap priority queue in order to traverse M in proper bottom-up order. That would push the time complexity to O(N * M * log(N * M)), so the memoization code is more efficient.)

    • So we can just iterate through every cell in M and run our recursive helper (dfs) which will fill in values in memo as it returns. For a given cell, if that cell’s solution has already been found, we can return it, otherwise we’ll take the best result of each of the four possible path directions.

    • Once the main iteration has finished, the highest value in memo will be our answer. so we should return it.

  • Implementation:
    • Python can make good use of @lru_cache instead of having to manually create a memoization data structure.
class Solution:
    def longestIncreasingPath(self, M: List[List[int]]) -> int:
        ylen, xlen = len(M), len(M[0])
        
        @lru_cache(maxsize=None)
        def dfs(y, x):
            val = M[y][x]
            return 1 + max(
                dfs(y+1, x) if y < ylen - 1 and val > M[y+1][x] else 0,
                dfs(y-1, x) if y > 0 and val > M[y-1][x] else 0, 
                dfs(y, x+1) if x < xlen - 1 and val > M[y][x+1] else 0,
                dfs(y, x-1) if x > 0 and val > M[y][x-1] else 0)
            
        return max(dfs(y, x) for y in range(ylen) for x in range(xlen))
  • Same approach; indexing using complex numbers:
class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        def length(z):
            if z not in memo:
                memo[z] = 1 + max([length(Z)
                                   for Z in (z+1, z-1, z+1j, z-1j)
                                   if Z in matrix and matrix[z] > matrix[Z]]
                                  or [0])
            return memo[z]
        memo = {}
        matrix = {i + j*1j: val
                  for i, row in enumerate(matrix)
                  for j, val in enumerate(row)}
                  
        return max(map(length, matrix) or [0])
Complexity
  • Time: \(O(mn)\) since we check the items of matrix just only one.
    • This looks like a graph problem. If we define $G=(V, E)$, where:
    • \(V=v_{i j}\) for \(0 \leq i<\mid\) matrix \(\mid\) and \(0 \leq j<\mid\) matrix \([i] \mid\)
    • \(E=(u, v)\) for \(u \epsilon V, v \epsilon\) neighbor \(s(u) \epsilon V\) and \(\operatorname{val}(u)<\operatorname{val}(v)\)
    • Now we need to find the longest path in the directed graph.
    • We can do a DFS from each vertex and track the max path length. DFS is \(O(V+E)\), but we have at most 4 edges per vertex in this graph, so this DFS is \(O(V)\). since we do it \(V\) times, the runtime is \(O\left(V^{2}\right)\). With caching, the DFS only has to touch each vertex once, so the total runtime is \(O(V)=O(m n)\).
  • Space: \(O(mn)\) for memoization.

Solution: Iterative/Bottom-up DP

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        matrix = {i + j*1j: val
                  for i, row in enumerate(matrix)
                  for j, val in enumerate(row)}
                  
        length = {}
        for z in sorted(matrix, key=matrix.get):
            length[z] = 1 + max([length[Z]
                                 for Z in (z+1, z-1, z+1j, z-1j)
                                 if Z in matrix and matrix[z] > matrix[Z]]
                                or [0])
            
        return max(length.values() or [0])
Complexity
  • Time: \(O(mn)\) since we check the items of matrix just only one.
    • This looks like a graph problem. If we define $G=(V, E)$, where:
    • \(V=v_{i j}\) for \(0 \leq i<\mid\) matrix \(\mid\) and \(0 \leq j<\mid\) matrix \([i] \mid\)
    • \(E=(u, v)\) for \(u \epsilon V, v \epsilon\) neighbor \(s(u) \epsilon V\) and \(\operatorname{val}(u)<\operatorname{val}(v)\)
    • Now we need to find the longest path in the directed graph.
    • We can do a DFS from each vertex and track the max path length. DFS is \(O(V+E)\), but we have at most 4 edges per vertex in this graph, so this DFS is \(O(V)\). since we do it \(V\) times, the runtime is \(O\left(V^{2}\right)\). With caching, the DFS only has to touch each vertex once, so the total runtime is \(O(V)=O(m n)\).
  • Space: \(O(mn)\) for dp

[516/Medium] Longest Palindromic Subsequence

Problem

  • Given a string s, find the longest palindromic subsequence’s length in s.

  • A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

  • Example 1:

Input: s = "bbbab"
Output: 4
Explanation: One possible longest palindromic subsequence is "bbbb".
  • Example 2:
Input: s = "cbbd"
Output: 2
Explanation: One possible longest palindromic subsequence is "bb".
  • Constraints:
    • 1 <= s.length <= 1000
    • s consists only of lowercase English letters.
  • See problem on LeetCode.

Solution: Top-down Recursive DP: If left == right, add 1; else chip one end at a time and take the max

class Solution:
    def longestPalindromeSubseq(self, s):
            """
            :type s: str
            :rtype: int
            """
            return self._longestPalindromeSubseq(s, 0, len(s) - 1, {})
        
        def _longestPalindromeSubseq(self, s, start, end, memo):
            key = (start, end)
            if key in memo:
                return memo[key]
            if start == end:
                return 1
                
            if start > end:
                return 0
            
            if s[start] == s[end]:
                memo[key] = self._longestPalindromeSubseq(s, start + 1, end - 1, memo) + 2
            else:
                memo[key] = max(
                    self._longestPalindromeSubseq(s, start + 1, end, memo),
                    self._longestPalindromeSubseq(s, start, end - 1, memo)
                )
            return memo[key]
  • lru_cache for memoization:
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        
        @lru_cache(None)
        def maxMatchCount(left, right):           
            if left > right:
                return 0
            
            if left == right:
                return 1            
            
            if s[left] == s[right]:
                # delve deeper into the string by chipping at both ends 
                # and add 2 for the current "left" and "right" match
                return maxMatchCount(left+1, right-1) + 2
            else:
                # if s[left] != s[right], chip one edge at a time and move ahead
                return max(maxMatchCount(left+1, right), maxMatchCount(left, right-1))
        
        return maxMatchCount(0, len(s)-1)
Complexity
  • Time: \(O(n^2)\)
  • Space: \(O(n^2)\) due to the callstacks for the recursion tree structure for maxMatchCount/_longestPalindromeSubseq and memoization memo

[518/Medium] Coin Change 2

Problem

  • You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

  • Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return 0.

  • You may assume that you have an infinite number of each kind of coin.

  • The answer is guaranteed to fit into a signed 32-bit integer.

  • Example 1:

Input: amount = 5, coins = [1,2,5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
  • Example 2:
Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.
  • Example 3:
Input: amount = 10, coins = [10]
Output: 1
  • Constraints:
    • 1 <= coins.length <= 300
    • 1 <= coins[i] <= 5000
    • All the values of coins are unique.
    • 0 <= amount <= 5000
  • See problem on LeetCode.

Solution: Bottom-up/Iterative DP

  • dp[i] is the number of combinations when amount = i, the target is to find dp[amount] where edge case is dp[0] = 1.

  • For each coin in coins, if the coin is selected, then i-coin must exist, that is, dp[i] = sum(dp[i-coin]).

  • Template:
    • This is a classical dynamic programming problem.
    • Here is a template one could use:
      • Define the base cases for which the answer is obvious.
      • Develop the strategy to compute more complex case from more simple one.
      • Link the answer to base cases with this strategy.
  • Example:
    • Let’s take an example: amount = 11, available coins - 2 cent, 5 cent and 10 cent. Note, that coins are unlimited.

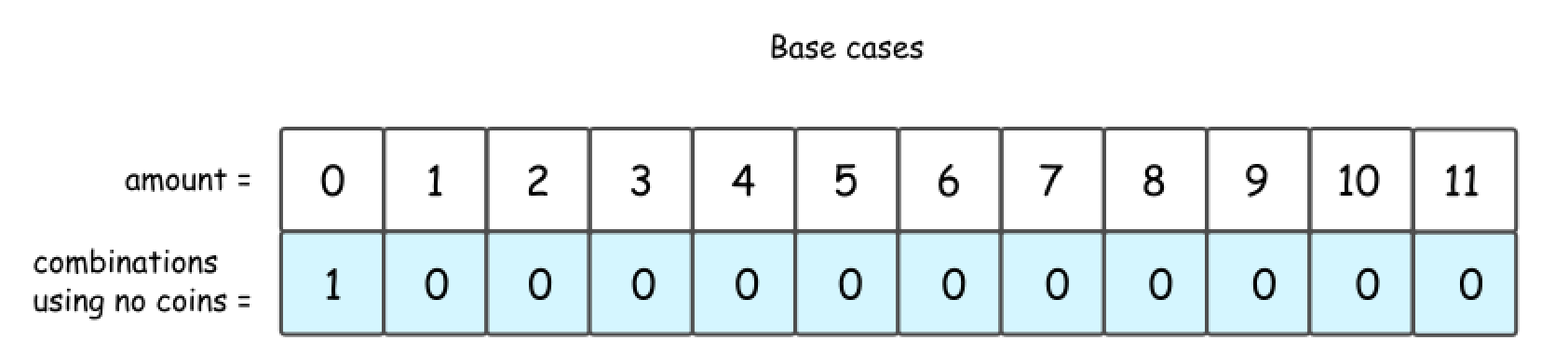
  • Base Cases: No Coins or Amount = 0
    • If the total amount of money is zero, there is only one combination: to take zero coins, hence dp[0] = 1.
    • Another base case is no coins: zero combinations for amount > 0 and one combination for amount == 0.

  • 2 Cent Coins
    • Let’s go one step further and consider the situation with one kind of available coins: 2 cent.

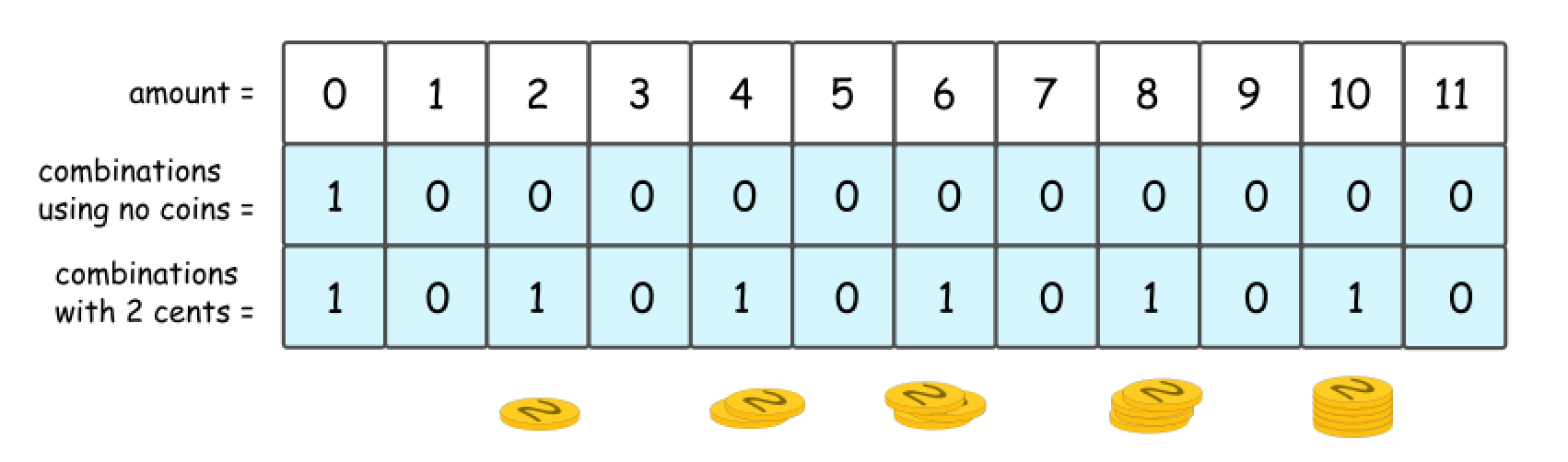
    • It’s quite evident that there could be 1 or 0 combinations here, 1 combination for even amount and 0 combinations for the odd one.

    • Note that the same answer could be received in a recursive way, by computing the number of combinations for all amounts of money, from 0 to 11.

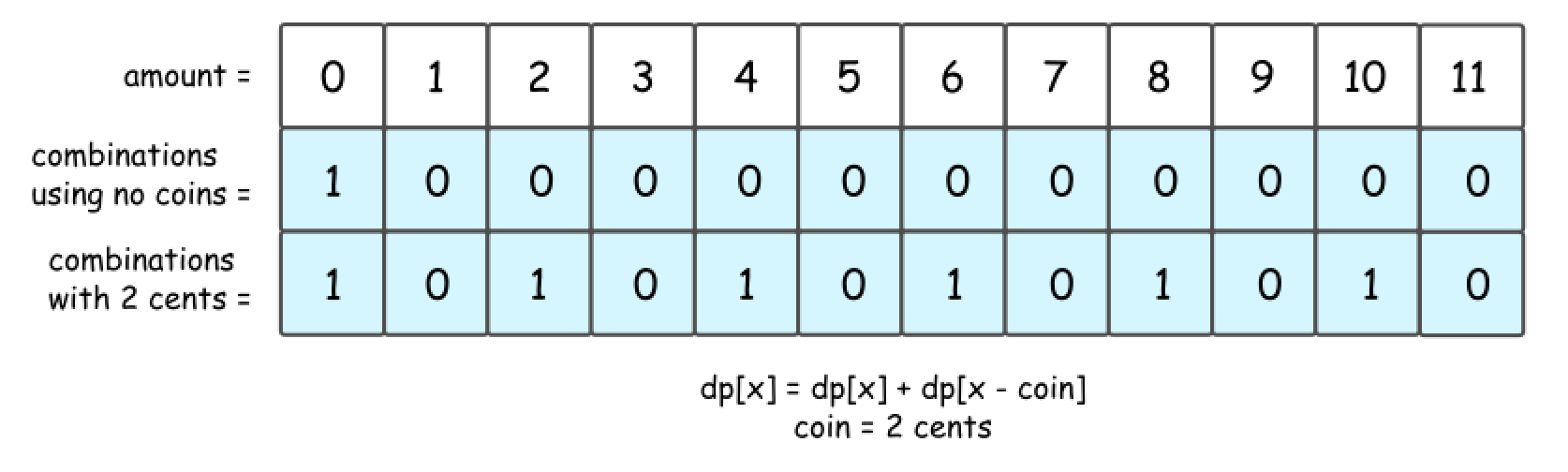
    • First, that’s quite obvious that all amounts less than 2 are not impacted by the presence of 2 cent coins. Hence for amount = 0 and for amount = 1 one could reuse the results from the figure 2.

    • Starting from amount = 2, one could use 2 cent coins in the combinations. Since the amounts are considered gradually from 2 to 11, at each given moment one could be sure to add not more than one coin to the previously known combinations.

    • So let’s pick up 2 cent coin, and use it to make up amount = 2. The number of combinations with this 2 cent coin is a number combinations for amount = 0, i.e. 1.

    • Now let’s pick up 2 cent coin, and use it to make up amount = 3. The number of combinations with this 2 cent coin is a number combinations for amount = 1, i.e. 0.

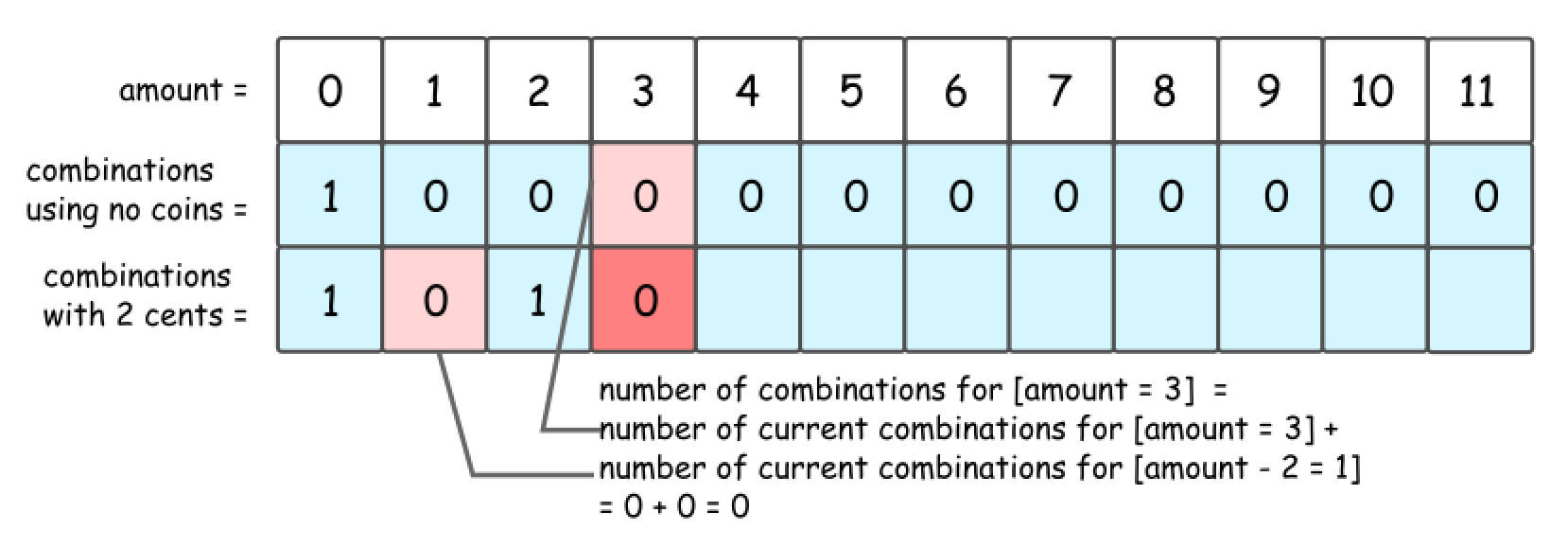
    • That leads to DP formula for number of combinations to make up the amount = x: dp[x] = dp[x] + dp[x - coin], where coin = 2 cents is a value of coins we’re currently adding.

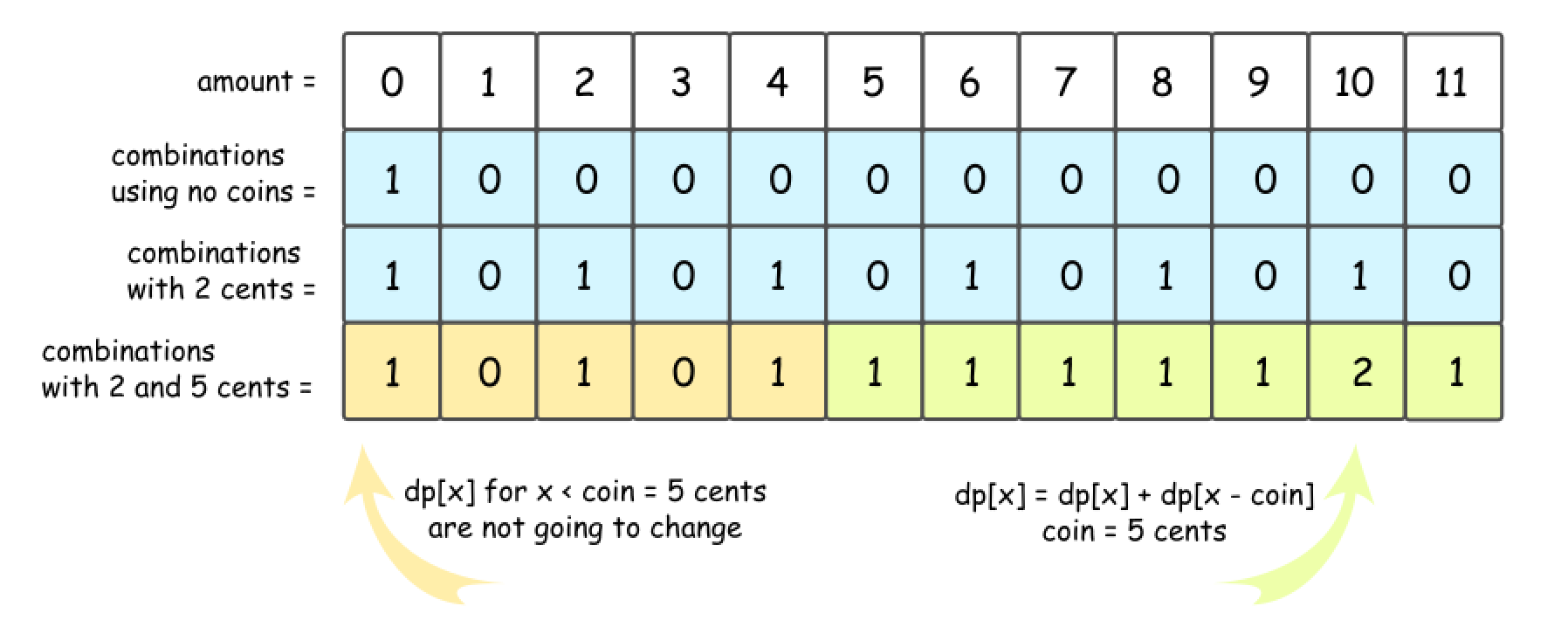
  • 2 Cent Coins + 5 Cent Coins + 10 Cent Coins
    • Now let’s add 5 cent coins. The formula is the same, but do not forget to add dp[x], number of combinations with 2 cent coins.

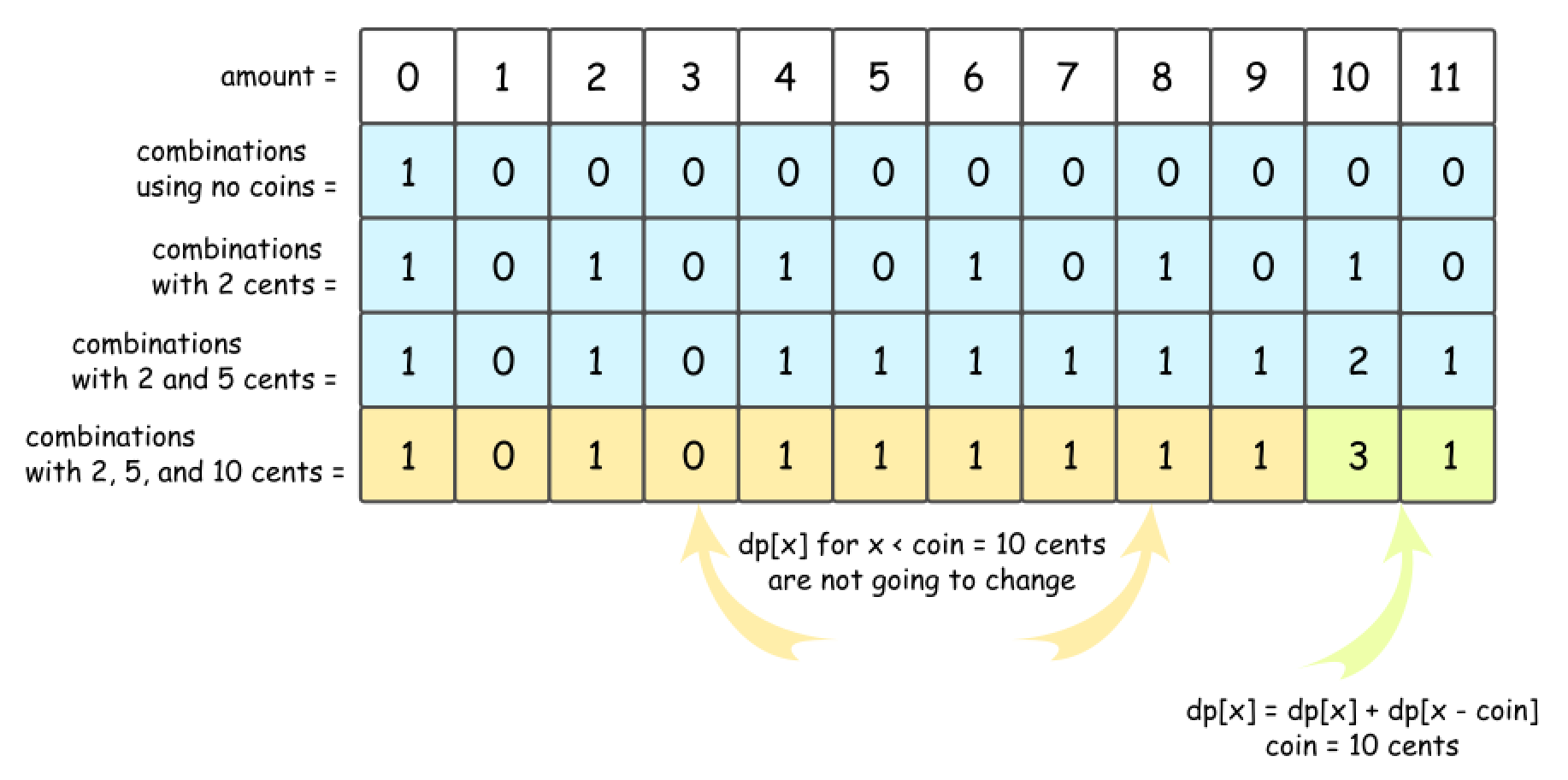
    • The story is the same for 10 cent coins.

  • Now the strategy is here:
    • Add coins one-by-one, starting from base case “no coins”.
    • For each added coin, compute recursively the number of combinations for each amount of money from 0 to amount.
  • Algorithm:
    • Initiate number of combinations array with the base case “no coins”: dp[0] = 1, and all the rest = 0.
    • Loop over all coins:
      • For each coin, loop over all amounts from 0 to amount:
      • For each amount x, compute the number of combinations: dp[x] += dp[x - coin].
    • Return dp[amount].
class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        dp = [0] * (amount + 1)
        dp[0] = 1
        
        for coin in coins:
            # for each coin, go from the difference in value of the current coin to the amount 
            # and add the number of combinations for (index-coin)
            # note that the loop starts from the value of the coin because a coin does not impact 
            # any combination counts less than it's value. 
            # as shown above -- consider value=2, all amounts less than 2 are not impacted by the presence of 2 cent coins.
            for index in range(coin, amount+1):
                dp[index] += dp[index-coin]
                
        return dp[amount]
Complexity
  • Time: \(O(n \times amount)\) where \(n\) is the length of the coins array.
  • Space: \(O(amount)\) for dp array.

[542/Medium] 01 Matrix

Problem

  • Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

  • The distance between two adjacent cells is 1.

  • Example 1:

Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]
  • Example 2:

Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]
  • Constraints:
    • m == mat.length
    • n == mat[i].length
    • 1 <= m, n <= 104
    • 1 <= m * n <= 104
    • mat[i][j] is either 0 or 1.
    • There is at least one 0 in mat.
  • See problem on LeetCode.

Solution: BFS

from collections import deque
class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        rows, cols = len(mat), len(mat[0])
        dir = [(1,0), (-1,0), (0,1), (0,-1)]
        q = deque()
        
        # iterate through whole matrix
        # add coords of 0s to queue
        # set non zero cells to #
        for r in range(rows):
            for c in range(cols):
                if mat[r][c] == 0:
                    q.append((r,c))
                else:
                    mat[r][c] = "#"
        
        # start bfs
        # first iterate through 0s and mark neighbors with corresponding values
        # append neighbors to queue for further exploration
        while q:
            r, c = q.popleft()
            for d in dir:
                nr, nc = r + d[0], c + d[1]
                if 0 <= nr < rows and 0 <= nc < cols and mat[nr][nc] == "#":
                    mat[nr][nc] = mat[r][c] + 1
                    q.append((nr, nc))
        return mat
Complexity
  • Time: \(O(r*c*\text{number of 0s})\) where \(r\) and \(c\) are the number of rows and cols in the input.
  • Space: \(O(r*c)\)

Solution: DP

  • Algorithm:

    • First calculate distance of cell based on its top and left cell.

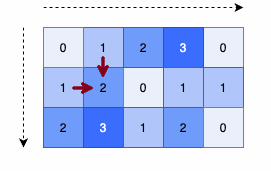
    • Second calculate distance of cell based on its bottom and right cell. 

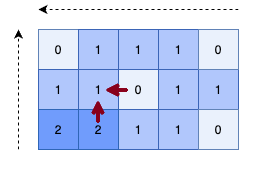
class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        
        rows = len(mat)
        cols = len(mat[0])
        
        # General idea:
        # First check if our current mat[r][c]>0, if so, lets update it to the min number to the top or left
        # Then lets do the same with bottom and right
        #0(r*c)^2
        for r in range(rows):
            for c in  range(cols):
                if mat[r][c] > 0:
                    top = mat[r - 1][c] if r > 0 else math.inf
                    left = mat[r][c - 1] if c > 0 else math.inf
                    mat[r][c] = 1 + min(top, left)
                    
        for r in range(rows - 1, -1, -1):
            for c in  range(cols - 1, -1, -1):
                if mat[r][c] > 0:
                    bottom = mat[r + 1][c] if r < rows - 1 else math.inf
                    right = mat[r][c + 1] if c < cols - 1 else math.inf
                    mat[r][c] = min(bottom + 1, right + 1, mat[r][c])
                    
        return mat
Complexity
  • Time: \(O(r*c)\) where \(r\) and \(c\) are the number of rows and cols in the input.
  • Space: \(O(1)\)

[689/Hard] Maximum Sum of 3 Non-Overlapping Subarrays

Problem

  • Given an integer array nums and an integer k, find three non-overlapping subarrays of length k with maximum sum and return them.

  • Return the result as a list of indices representing the starting position of each interval (0-indexed). If there are multiple answers, return the lexicographically smallest one.

  • Example 1:

Input: nums = [1,2,1,2,6,7,5,1], k = 2
Output: [0,3,5]
Explanation: Subarrays [1, 2], [2, 6], [7, 5] correspond to the starting indices [0, 3, 5].
We could have also taken [2, 1], but an answer of [1, 3, 5] would be lexicographically larger.
  • Example 2:
Input: nums = [1,2,1,2,1,2,1,2,1], k = 2
Output: [0,2,4]
  • Constraints:
    • 1 <= nums.length <= 2 * 104
    • 1 <= nums[i] < 216
    • 1 <= k <= floor(nums.length / 3)
  • See problem on LeetCode.

Solution: Brute force

  • One thing you’ll notice, if you do the brute force, is how many overlapping sub problems there are. This is a good place to start, because it can lead into the intuition for how DP might work. You try every index, and every non overlapping k-th window offset from that window, and then every k-th window offset from the offset window. You literally try every solution.
class Solution:
    def maxSumOfThreeSubarraysCustom(self, nums: List[int], k: int) -> List[int]:    
        maxS = float('-inf')
        res = []

        # e1, e2, e3 are ending indices of first, second and third intervals.
        for e1 in range(k-1, N - 2*k):
            s1 = e1 - k + 1
            for e2 in range(e1+k, N - k):
                s2 = e2 - k + 1
                for e3 in range(e2+k, N):
                    s3 = e3 - k + 1
                    tsum = dp[e1] + dp[e2] + dp[e3] 
                    if tsum > maxS:
                        maxS = tsum
                        res = [s1, s2, s3]
                        
        return res
Complexity
  • Time: \(O(n^3)\)
  • Space: \(O(1)\)

Solution: Top Down DP without Memoization

  • The idea here is similar, but implemented in a recursive top down approach. Note that this will also TLE, but gives use a better understanding of how caching might be implemented to save overlapping sub problems.
class Solution:
    def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:
        res = self.window_sum(nums, k, 0, 0)
        return res[1]

    def window_sum(self, nums, k, idx, used):
        # we can only have 3 windows at a time
        if used == 3:
            return 0, []

        # are we going to overflow over our nums array?
        if idx - (used * k) > (len(nums)):
            return 0, []

        take_curr_sum, take_curr_indices = self.window_sum(nums, k, idx + k, used + 1)
        take_curr_sum += sum(nums[idx:idx + k])

        skip_curr_sum, skip_curr_indices = self.window_sum(nums, k, idx + 1, used)

        if take_curr_sum >= skip_curr_sum:
            return take_curr_sum, ([idx] + take_curr_indices)
        else:
            return skip_curr_sum, skip_curr_indices
Complexity
  • Time: \(O(2^n)\)
  • Space: \(O(n)\)

Solution: Top down with Memo

  • It’s very slow, but with the memo solution this is close to a true O(n) sol. Note that this can be sped up using a prefix sum array, which will allow us to look up the sums of any interval between indices.
class Solution:
    def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:
        memo = {}
        res = self.window_sum(nums, k, 0, 0, memo)
        return res[1]

    def window_sum(self, nums, k, idx, used, memo):
        # we can only have 3 windows at a time
        if used == 3:
            return 0, []

        # are we going to overflow over our nums array?
        if idx - (used * k) > (len(nums)):
            return 0, []

        if (idx, used) in memo:
            return memo[(idx, used)]

        take_curr_sum, take_curr_indices = self.window_sum(nums, k, idx + k, used + 1, memo)
        take_curr_sum += sum(nums[idx:idx + k])

        skip_curr_sum, skip_curr_indices = self.window_sum(nums, k, idx + 1, used, memo)

        if take_curr_sum >= skip_curr_sum:
            memo[(idx, used)] = (take_curr_sum, ([idx] + take_curr_indices))
            return memo[(idx, used)]
        else:
            memo[(idx, used)] = (skip_curr_sum, skip_curr_indices)
            return memo[(idx, used)]
Complexity
  • Time: \(O(n^2)\) due to sum(nums[idx:idx + k]) but could be O(n) using prefix sum.
  • Space: \(O(n)\)

Solution: DFS

  • Simple DFS + memoization solution.
  • Algorithm:
    • Use prefix sum, in order to compute the sum in a certain range in \(O(N)\) and later accesses in \(O(1)\).
    • DFS approach with 2 options: take \(k\) elements or skip the current element. During backtracking we take the solution with maximum sum. To obtain the lexicographically smallest one, we update the best solution even when the total sum is the same.
class Solution:
    def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:
        def get_prefix_sum():
            prefix_sum = [0]*(L+1)
            
            for i in range(L):
                prefix_sum[i+1] = prefix_sum[i] + nums[i]
                
            return prefix_sum
            
        def dfs(i, N): #(i: index in nums, N: numbers of subarrays)
            if not N:
                return [], 0
            if L-i < k*N:
                return None, -float("inf")
            if (i, N) in memo:
                return memo[(i, N)]
                
            # 2 options: take k elements or skip current value
            include, cnt_in = dfs(i+k, N-1) # take k elements
            include, cnt_in = [i] + include, cnt_in+prefix_sum[i+k]-prefix_sum[i] # build array and sum during backtracking
            exclude, cnt_ex = dfs(i+1, N) # skip current value
            if cnt_in >= cnt_ex:  # to obtain the lexicographically smallest one
                memo[(i,N)] = include, cnt_in
            else:
                memo[(i,N)] = exclude, cnt_ex
            return memo[(i,N)]
            
        memo = {}
        L = len(nums)
        prefix_sum = get_prefix_sum()
        return dfs(0, 3)[0]

Solution: Sliding Window

  • The code below is an extension of this problem for unlimited \(m\) sliding windows. Note that \(m=3\) is just one case.

  • The basic principles are the standard:

    • We create a new sliding_window[i], and use the results from our previous iterations to track the maximum value behind it. In this way, we can create generations of optimal results for a growing number of windows.

    • The process can be initialized with an empty array of zeros (nothing found behind the first window).

    • At every step, we discard any results that didn’t create a new maximum (and copy our old values instead).

class Solution:
    def makeS(self,nums,k):
        s = sum(nums[:k])
        S = [ s ]
        for i in range(k,len(nums)):
            s += nums[i] - nums[i-k]
            S.append( s )
        return S
        
    def maxSumOfThreeSubarrays(self, nums, k, m = 3):
        L = len(nums)
        if (k*m)>=L:
            return sum( nums )
        #
        S    = self.makeS(nums,k)
        Aprev = [ [0,[]] for _ in range(L) ]
        for i in range(m):
            Anew  = [ [ Aprev[0][0]+S[i*k], Aprev[0][1] + [i*k] ] ]
            for j in range(i*k+1,len(S)):
                sp,ip = Aprev[j-i*k]
                s = S[j] + sp
                if s>Anew[-1][0]:
                    Anew.append( [s, ip + [j] ] )
                else:
                    Anew.append( Anew[-1] )
            Aprev = Anew
        return Anew[-1][-1]
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

[983/Hard] Minimum Cost For Tickets

Problem

  • Given an integer array nums and an integer k, find three non-overlapping subarrays of length k with maximum sum and return them.

  • Return the result as a list of indices representing the starting position of each interval (0-indexed). If there are multiple answers, return the lexicographically smallest one.

  • Example 1:

Input: nums = [1,2,1,2,6,7,5,1], k = 2
Output: [0,3,5]
Explanation: Subarrays [1, 2], [2, 6], [7, 5] correspond to the starting indices [0, 3, 5].
We could have also taken [2, 1], but an answer of [1, 3, 5] would be lexicographically larger.
  • Example 2:
Input: nums = [1,2,1,2,1,2,1,2,1], k = 2
Output: [0,2,4]
  • Constraints:
    • 1 <= nums.length <= 2 * 104
    • 1 <= nums[i] < 216
    • 1 <= k <= floor(nums.length / 3)
  • See problem on LeetCode.

Solution: Top-down DP with Recursion + Memoization

class Solution:
    def mincostTickets(self, days: List[int], costs: List[int]) -> int:
        # to speed up element checking for days
        travel_days = set(days)
        
        # use python built-in cache as memoization for DP
        @cache
        def dp(day_d):
            # Base case
            if day_d == 0:
                # no cost on before traveling
                return 0
            
            # General cases
            if day_d not in travel_days:
                # no extra cost on non-travel day
                return dp(day_d-1)
            else:
                # compute minimal cost on travel day
                with_1_day_pass = dp(max(0, day_d - 1)) + costs[0]
                with_7_day_pass = dp(max(0, day_d - 7) ) + costs[1]
                with_30_day_pass = dp(max(0, day_d - 30)) + costs[2]
                
                return min(with_1_day_pass, with_7_day_pass, with_30_day_pass)
            
        last_travel_day = days[-1]
        
        # Cost on last travel day of this year is the answer
        return dp(last_travel_day)

Solution: Bottoms-up DP with Iteration (i.e., Tabulation Method)

  • dp[i] means overall costs until the i-th day (included)
  • We have to check two conditions:
    1. i in days list:
      • We have three options:
        • 1-pass: dp[i] = dp[i-1] + costs[0]
        • 7-pass: dp[i] = dp[i-7] + costs[1]
        • 30-pass: dp[i] = dp[i-30] + costs[2]
      • In order to avoid invalid/negative indexes which are out-of-boundary:
        • 1-pass: dp[i] = dp[max(0,i-1)] + costs[0]
        • 7-pass: dp[i] = dp[max(0,i-7)] + costs[1]
        • 30-pass: dp[i] = dp[max(0,i-30)] + costs[2]
    2. i not in days: dp[i] = dp[i-1]
      • which simply means we don’t have to spend money, and total costs remains same.
class Solution:
    def mincostTickets(self, days: List[int], costs: List[int]) -> int:
        # set of travel days
        dy = set(days)
        
        # last travel day
        last_travel_day = days[-1]
        
        # Base case: no cost before first day (i.e., no travel)
        # DP Table, record for minimum cost of ticket to travel
        dp = [0 for _ in range(last_travel_day+1)]        
        
        # Solve min cost by Dynamic Programming        
        for i in range(last_travel_day+1):
            if i not in dy: 
                # Today is not a traveling day, so no extra cost
                dp[i] = dp[i-1]
            # For traveling day
            else: 
                # Compute minimum cost for subproblem using DP
                # cost[0]: the cost of 1-day-pass ticket
                # cost[1]: the cost of 7-day-pass ticket
                # cost[2]: the cost of 30-day-pass ticket
                dp[i] = min(dp[max(0, i-1)] + costs[0], dp[max(0, i-7)] + costs[1], dp[max(0, i-30)] + costs[2])

        # Cost on last travel day of this year is the answer                
        return dp[-1]
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\) where \(n\) = last day in days list + 1
    • Note that the max time and space complexity is \(O(366)\)

[1048/Medium] Longest String Chain

Problem

  • You are given an array of words where each word consists of lowercase English letters.
  • wordA is a predecessor of wordB if and only if we can insert exactly one letter anywhere in wordA without changing the order of the other characters to make it equal to wordB.
    • For example, “abc” is a predecessor of “abac”, while “cba” is not a predecessor of “bcad”.
  • A word chain is a sequence of words [word1, word2, ..., wordk] with k >= 1, where word1 is a predecessor of word2, word2 is a predecessor of word3, and so on. A single word is trivially a word chain with k == 1.

  • Return the length of the longest possible word chain with words chosen from the given list of words.

  • Example 1:
Input: words = ["a","b","ba","bca","bda","bdca"]
Output: 4
Explanation: One of the longest word chains is ["a","ba","bda","bdca"].
  • Example 2:
Input: words = ["xbc","pcxbcf","xb","cxbc","pcxbc"]
Output: 5
Explanation: All the words can be put in a word chain ["xb", "xbc", "cxbc", "pcxbc", "pcxbcf"].
  • Example 3:
Input: words = ["abcd","dbqca"]
Output: 1
Explanation: The trivial word chain ["abcd"] is one of the longest word chains.
["abcd","dbqca"] is not a valid word chain because the ordering of the letters is changed.
  • Constraints:
    • 1 <= words.length <= 1000
    • 1 <= words[i].length <= 16
    • words[i] only consists of lowercase English letters.
  • See problem on LeetCode.

Solution

  • A naive approach would be to check every word against every other word looking for predecessors, but that would lead to a TLE result. The first important realization that we should be able to make is that while a word may have many 26 * (word.length + 1) possible successors, it can only have word.length predecessors.

  • So rather than iterating from small to large words and checking every combination for a link, we can store the words in a set and only check the few possible predecessors while iterating from large to small. To aid in that, we can actually separate words into an array of sets (W) indexed by word length, so that we can directly access batches of words by their length.

  • (Note: As we iterate backward through W, if we find that W[i-1] is empty, we don’t need to process the words in W[i], since there cannot possibly be a predecessor match.)

  • Then we can use a dynamic programming (DP) approach to eliminate some common sub-problems. We can define a hashmap (dp) where dp[word] is the length of the longest chain ending at word found so far.

  • So at each word, we’ll iterate through each of its predecessors (pred) and check the appropriate set in W for a match. If we find a match, we can update dp[pred] if dp[word] + 1 is better, increasing the chain by one. We should also separately keep track of the best chain length we’ve seen, so that once we reach the end, we can just return best.

class Solution:
    def longestStrChain(self, words: List[str]) -> int:
        W = [set() for _ in range(17)]
        
        for word in words:
            W[len(word)].add(word)
        dp, best = defaultdict(lambda:1), 1
        
        for i in range(16, 0, -1):
            if len(W[i-1]) == 0: 
                continue
            
            for word in W[i]:
                wVal = dp[word]
                for j in range(len(word)):
                    pred = word[0:j] + word[j+1:]
                    if pred in W[i-1] and wVal >= (dp.get(pred) or 1):
                        dp[pred] = wVal + 1
                        best = max(best, wVal + 1)
                        
        return best
Complexity
  • Time Complexity: \(O(n*m)\) where \(n\) is the length of words and \(m\) is the average length of the words in words.
  • Space Complexity: \(O(n + p)\) where \(p\) is the number of predecessors found and stored in dp.

[1143/Medium] Longest Common Subsequence

Problem

  • Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
  • A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
    • For example, "ace" is a subsequence of "abcde".

  • A common subsequence of two strings is a subsequence that is common to both strings.

  • Example 1:
Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.
  • Example 2:
Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.
  • Example 3:
Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.
  • Constraints:
    • 1 <= text1.length, text2.length <= 1000
    • text1 and text2 consist of only lowercase English characters.
  • See problem on LeetCode.

Solution: Memoization

  • This is a nice problem, as unlike some interview questions, this one is a real-world problem! Finding the longest common subsequence between two strings is useful for checking the difference between two files (diffing). Git needs to do this when merging branches. It’s also used in genetic analysis (combined with other algorithms) as a measure of similarity between two genetic codes.
  • For that reason, the examples used in this article will be strings consisting of the letters a, c, g, and t. You might remember these letters from high school biology—they are the symbols we use to represent genetic codes. By using just four letters in examples, it is easier for us to construct interesting examples to discuss here. You don’t need to know anything about genetics or biology for this though, so don’t worry.

  • Before we look at approaches that do work, we’ll have a quick look at some that do not. This is because we’re going to pretend that you’ve just encountered this problem in an interview, and have never seen it before, and have not been told that it is a “dynamic programming problem”. After all, in this interview scenario, most people won’t realize immediately that this is a dynamic programming problem. Being able to approach and explore problems with an open mind without jumping to early conclusions is essential in tackling problems you haven’t seen before.

  • What is a Common Subsequence?
    • Here’s an example of two strings that we need to find the longest common subsequence of.

    • A common subsequence is a sequence of letters that appears in both strings. Not every letter in the strings has to be used, but letters cannot be rearranged. In essence, a subsequence of a string s is a string we get by deleting some letters in s.
    • Here are some of the common subsequences for the above example. To help show that the subsequence really is a common subsequence, we’ve drawn lines between the corresponding characters.

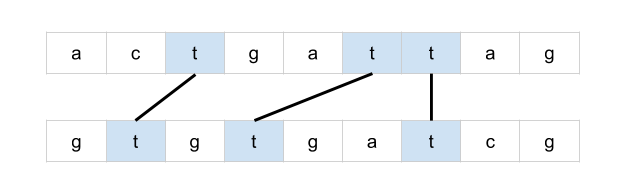
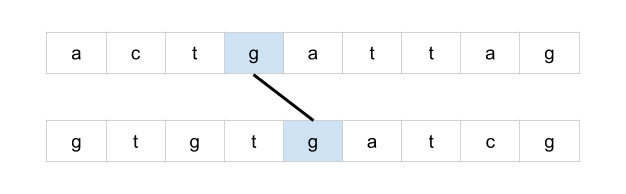
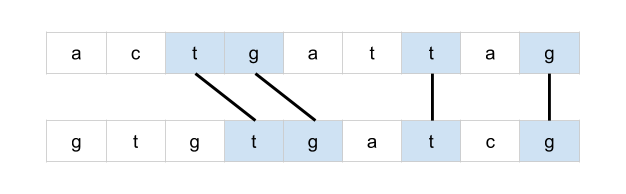
    • Drawing lines between corresponding letters is a great way of visualizing the problem and is potentially a valuable technique to use on a whiteboard during an interview. Observe that if lines cross over each other, then they do not represent a common subsequence.

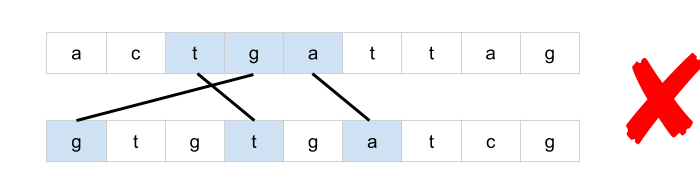
    • This is because lines that cross over are representing letters that have been rearranged.

    • We will use and refer to “lines” between the words extensively throughout this article.

  • Brute-force:

    • The most obvious approach would be to iterate through each subsequence of the first string and check whether or not it is also a subsequence of the second string.
    • This, however, will require exponential time to run. The number of subsequences in a string is up to \(2^L\), where \(L\) is the length of the string. This is because, for each character, we have two choices; it can either be in the subsequence or not in it. Duplicates characters reduce the number of unique subsequences a bit, although in the general case, it’s still exponential.
    • This would be a brute-force approach.

  • Greedy:

    • By this point, it’s hopefully clear that we’re dealing with an optimization problem. We need to generate a common subsequence that has the maximum possible number of letters. Using our analogy of drawing lines between the words, we could also phrase it as maximizing the number of non-crossing lines.
    • There are a couple of strategies we use to design a tractable (non-exponential) algorithm for an optimization problem.
      1. Identifying a greedy algorithm
      2. Dynamic programming
    • There is no guarantee that either is possible. Additionally, greedy algorithms are strictly less common than dynamic programming algorithms and are often more difficult to identify. However, if a greedy algorithm exists, then it will almost always be better than a dynamic programming one. You should, therefore, at least give some thought to the potential existence of a greedy algorithm before jumping straight into dynamic programming.
    • The best way of doing this is by drawing an example and playing around with it. One idea could be to iterate through the letters in the first word, checking whether or not it is possible to draw a line from it to the second word (without crossing lines). If it is, then draw the left-most line possible.
    • For example, here’s what we would do with the first letter of our example from earlier.

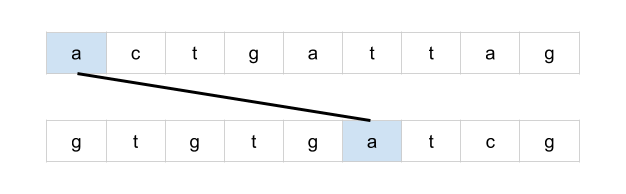
    • And then, the second letter.

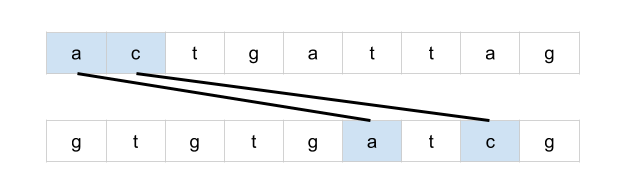
    • And finally, the third letter.

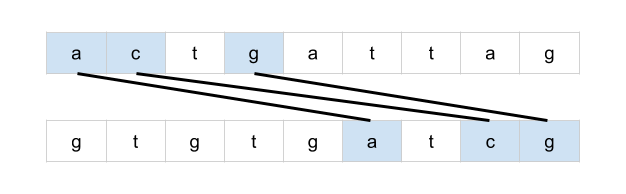
    • This solution, however, isn’t optimal. Here is a better solution.

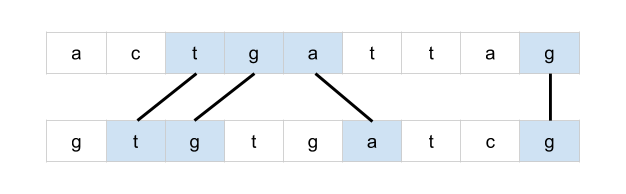
    • What if we were to do the same, but instead going from the second word to the first word? Perhaps one way or the other will always be optimal?

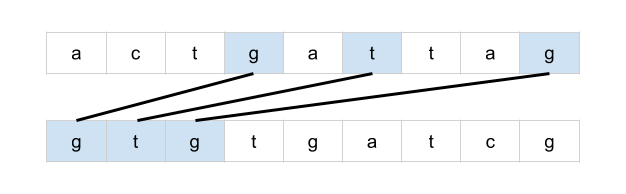
    • Unfortunately, this hasn’t worked either. This solution is still worse than a better one we know about.
    • Perhaps, instead, we could draw all possible lines. Could there be a way of eliminating some of the lines that cross over?

    • Uhoh, we now have what looks like an even more complicated problem than the one we began with. With some lines crossing over many other lines, where would you even begin?
  • Applying Dynamic Programming to a Problem:
    • While it’s very difficult to be certain that there is no greedy algorithm for your interview problem, over time you’ll build up an intuition about when to give up. You also don’t want to risk spending so long trying to find a greedy algorithm that you run out of time to write a dynamic programming one (and it’s also best to make sure you write a working solution!).
    • Besides, sometimes the process used to develop a dynamic programming solution can lead to a greedy one. So, you might end up being able to further optimize your dynamic programming solution anyway.
    • Recall that there are two different techniques we can use to implement a dynamic programming solution; memoization and tabulation.
      • Memoization is where we add caching to a function (that has no side effects). In dynamic programming, it is typically used on recursive functions for a top-down solution that starts with the initial problem and then recursively calls itself to solve smaller problems.
      • Tabulation uses a table to keep track of subproblem results and works in a bottom-up manner: solving the smallest subproblems before the large ones, in an iterative manner. Often, people use the words “tabulation” and “dynamic programming” interchangeably.
    • For most people, it’s easiest to start by coming up with a recursive brute-force solution and then adding memoization to it. After that, they then figure out how to convert it into an (often more desired) bottom-up tabulated algorithm.

  • Intuition:

    • The first step is to find a way to recursively break the original problem down into subproblems. We want to find subproblems such that we can create an optimal solution from the results of those subproblems.
    • Earlier, we were drawing lines between identical letters.

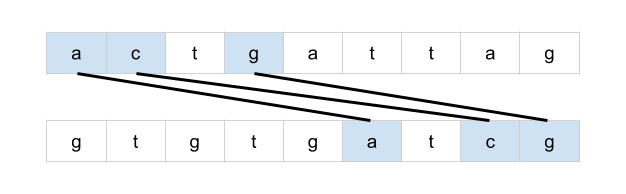
    • Consider the greedy algorithm we tried earlier where we took the first possible line. Instead of assuming that the line is part of the optimal solution, we could consider both cases: the line is part of the optimal solution or the line is not part of the optimal solution.

    • If the line is part of the optimal solution, then we know that the rest of the lines must be in the substrings that follow the line. As such, we should find the solution for the substrings, and add 1 onto the result (for the new line) to get the optimal solution.

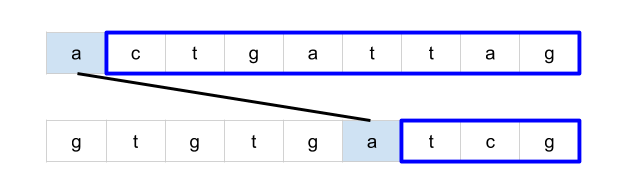
    • However, if the line is not part of the optimal solution, then we know that the letter in the first string is not included (as this would have been the best possible line for that letter). So, instead, we remove the first letter of the first string and treat the remainder as the subproblem. Its solution will be the optimal solution.

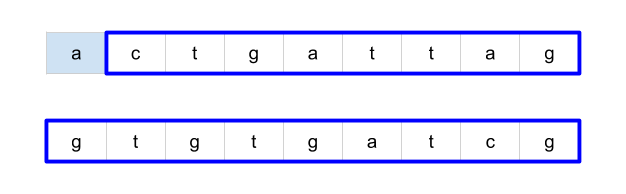
    • But remember, we don’t know which of these two cases is true. As such, we need to compute the answer for both cases. The highest one will be the optimal solution and should be returned as the answer for this problem.

    • Note that if either the first string or the second string is of length 0, we don’t need to break it into subproblems and can just return 0. This acts as the base case for the recursion.

    • But how many total subproblems will we need to solve? Well, because we always take a character off one, or both, of the strings each time, there are \(M \cdot N\) possible subproblems (where \(M\) is the length of the first string, and \(N\) the length of the second string). Another way of seeing this is that subproblems are represented as suffixes of the original strings. A string of length \(K\) has \(K\) unique suffixes. Therefore, the first string has MM suffixes, and the second string has NN suffixes. There are, therefore, \(M \cdot N\) possible pairs of suffixes.

    • Some subproblems may be visited multiple times, for example LCS("aac", "adf") has the two subproblems LCS("ac", "df") and LCS("ac", "adf"). Both of these share a common subproblem of LCS("c", "df"). As such, as we should memoize the results of LCS calls so that the answers of previously computed subproblems can immediately be returned without the need for re-computation.

  • Algorithm:

    • From what we’ve explored in the intuition section, we can create a top-down recursive algorithm that looks like this in pseudocode:
      define function LCS(text1, text2):
      # If either string is empty there, can be no common subsequence.
      if length of text1 or text2 is 0:
          return 0

      letter1 = the first letter in text1
      firstOccurence = first position of letter1 in text2

      # The case where the line *is not* part of the optimal solution
      case1 = LCS(text1.substring(1), text2)

      # The case where the line *is* part of the optimal solution
      case2 = 1 + LCS(text1.substring(1), text2.substring(firstOccurence + 1))
       
      return maximum of case1 and case2
    • You might notice from the pseudocode that there’s one case we haven’t handled: if letter1 isn’t part of text2, then we can’t solve the first subproblem. However, in this case, we can simply ignore the first subproblem as the line doesn’t exist. This leaves us with:
      define function LCS(text1, text2):
      # If either string is empty there can be no common subsequence
      if length of text1 or text2 is 0:
          return 0

      letter1 = the first letter in text1

      # The case where the line *is not* part of the optimal solution
      case1 = LCS(text1.substring(1), text2)

      case2 = 0
      if letter1 is in text2:
          firstOccurence = first position of letter1 in text2
          # The case where the line *is* part of the optimal solution
          case2 = 1 + LCS(text1.substring(1), text2.substring(firstOccurence + 1))

      return maximum of case1 and case2
    • Remember, we need to make sure that the results of this method are memoized. In Python, we can use lru_cache. In Java, we need to make our own data structure. A 2D Array is the best option (see the code for the details of how this works).
      from functools import lru_cache

  class Solution:
      def longestCommonSubsequence(self, text1: str, text2: str) -> int:
            
          @lru_cache(maxsize=None)
          def memo_solve(p1, p2):
                
              # Base case: If either string is now empty, we can't match
              # up anymore characters.
              if p1 == len(text1) or p2 == len(text2):
                  return 0
                
              # Option 1: We don't include text1[p1] in the solution.
              option_1 = memo_solve(p1 + 1, p2)
                
              # Option 2: We include text1[p1] in the solution, as long as
              # a match for it in text2 at or after p2 exists.
              first_occurence = text2.find(text1[p1], p2)
              option_2 = 0
              if first_occurence != -1:
                  option_2 = 1 + memo_solve(p1 + 1, first_occurence + 1)
                
              # Return the best option.
              return max(option_1, option_2)
                    
          return memo_solve(0, 0)
Complexity
  • Time: \(O(M \cdot N^2)\).
    • We analyze a memoized-recursive function by looking at how many unique subproblems it will solve, and then what the cost of solving each subproblem is.
    • The input parameters to the recursive function are a pair of integers; representing a position in each string. There are \(M\) possible positions for the first string, and \(N\) for the second string. Therefore, this gives us \(M \cdot N\) possible pairs of integers, and is the number of subproblems to be solved.
    • Solving each subproblem requires, in the worst case, an \(O(N)\) operation; searching for a character in a string of length NN. This gives us a total of \((M \cdot N^2)\).
  • Space: \(O(M \cdot N)\).
    • We need to store the answer for each of the \(M \cdot N\) subproblems. Each subproblem takes \(O(1)\) space to store. This gives us a total of \(O(M \cdot N)\).
    • It is important to note that the time complexity given here is an upper bound. In practice, many of the subproblems are unreachable, and therefore not solved.
    • For example, if the first letter of the first string is not in the second string, then only one subproblem that has the entire first word is even considered (as opposed to the \(N\) possible subproblems that have it). This is because when we search for the letter, we skip indices until we find the letter, skipping over a subproblem at each iteration. In the case of the letter not being present, no further subproblems are even solved with that particular first string.

Solution: Improved Memoization

  • Intuition:
    • There is an alternative way of expressing the solution recursively. The code is simpler, and will also translate a lot more easily into a bottom-up dynamic programming approach.
    • The subproblems are of the same structure as before; represented as two indexes. Also, like before, we’re going to be considering multiple possible decisions and then going with the one that has the highest answer. The difference is that the way we break a problem into subproblems is a bit different. For example, here is how our example from before breaks into subproblems.

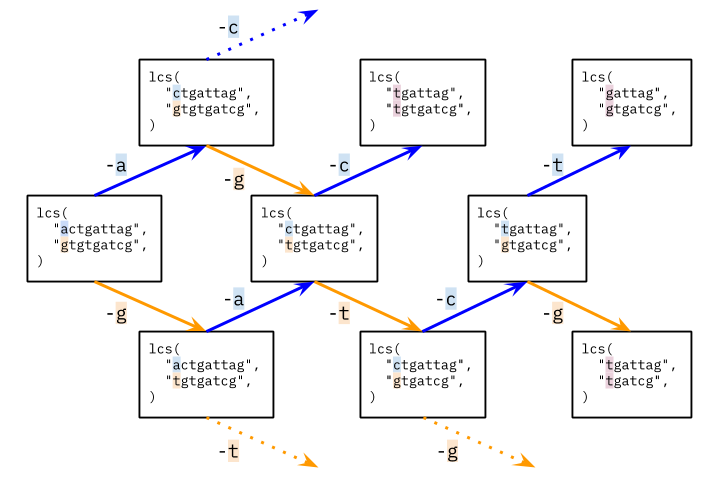
    If the first character of each string is not the same, then either one or both of those characters will not be used in the final result (i.e. not have a line drawn to or from it). Therefore, the length of the longest common subsequence is max(LCS(p1 + 1, p2), LCS(p1, p2 + 1)).

    • Now, what about subproblems such as LCS(“tgattag”, “tgtgatcg”)? The first letter of each string is the same, and so we could draw a line between them. Should we? Well, there is no reason not to draw a line between the first characters when they’re the same. This is because it won’t block any later (optimal) decisions. No letters other than those used for the line are removed from consideration by it. Therefore, we don’t need to make a decision in this case.

    When the first character of each string is the same, the length of the longest common subsequence is 1 + LCS(p1 + 1, p2 + 1). In other words, we draw a line a line between the first two characters, adding 1 to the length to represent that line, and then solving the resulting subproblem (that has the first character removed from each string).

    • Here is a few more of the subproblems for the above example.

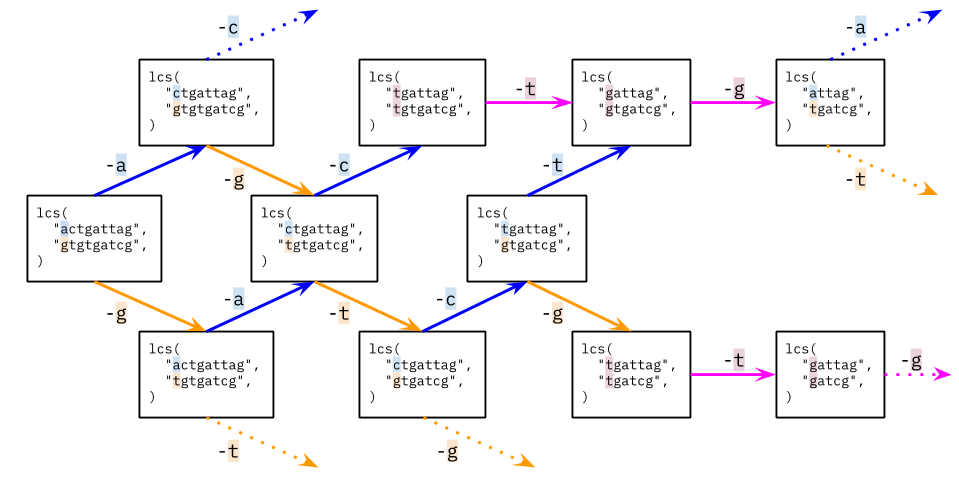
    • Like before, we still have overlapping subproblems, i.e. subproblems that appear on more than one branch. Therefore, we should still be using a memoization table, just like before.

  • Algorithm:

      from functools import lru_cache
  class Solution:
      def longestCommonSubsequence(self, text1: str, text2: str) -> int:
            
          @lru_cache(maxsize=None)
          def memo_solve(p1, p2):
                
              # Base case: If either string is now empty, we can't match
              # up anymore characters.
              if p1 == len(text1) or p2 == len(text2):
                  return 0
                
              # Recursive case 1.
              if text1[p1] == text2[p2]:
                  return 1 + memo_solve(p1 + 1, p2 + 1)
                
              # Recursive case 2.
              else:
                  return max(memo_solve(p1, p2 + 1), memo_solve(p1 + 1, p2))
                
          return memo_solve(0, 0)
Complexity
  • Time: \(O(M \cdot N)\).
    • This time, solving each subproblem has a cost of \(O(1)\). Again, there are \(M \cdot N\) subproblems, and so we get a total time complexity of \(O(M \cdot N)\).
  • Space: \(O(M \cdot N)\).
    • We need to store the answer for each of the \(M \cdot N\) subproblems.

Solution: Dynamic Programming

  • Intuition:
    • In many programming languages, iteration is faster than recursion. Therefore, we often want to convert a top-down memoization approach into a bottom-up dynamic programming one (some people go directly to bottom-up, but most people find it easier to come up with a recursive top-down approach first and then convert it; either way is fine).

    Observe that the subproblems have a natural “size” ordering; the largest subproblem is the one we start with, and the smallest subproblems are the ones with just one letter left in each word. The answer for each subproblem depends on the answers to some of the smaller subproblems.

    • Remembering too that each subproblem is represented as a pair of indexes, and that there are text1.length() * text2.length() such possible subproblems, we can iterate through the subproblems, starting from the smallest ones, and storing the answer for each. When we get to the larger subproblems, the smaller ones that they depend on will already have been solved. The best way to do this is to use a 2D array.

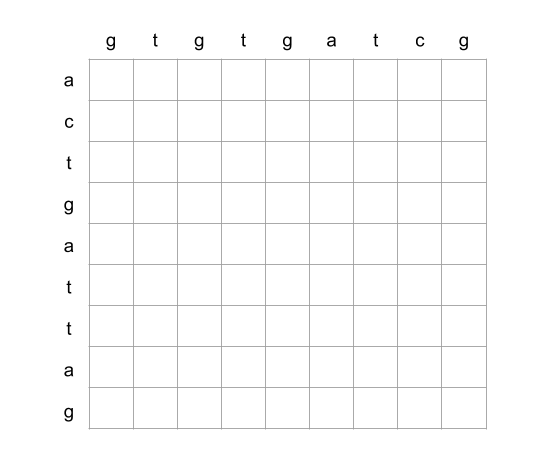
    • Each cell represents one subproblem. For example, the below cell represents the subproblem lcs("attag", "gtgatcg").

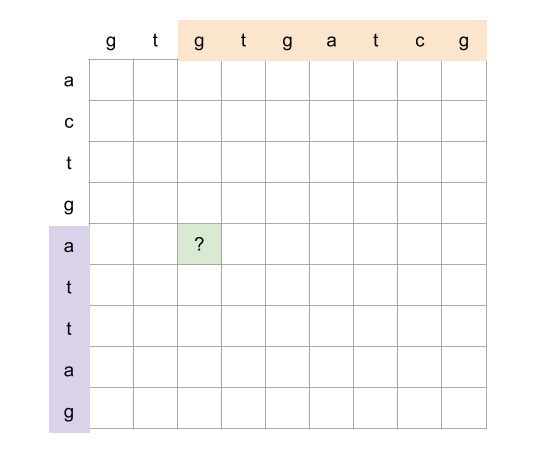
    • Remembering back to Approach 2, there were two cases.
      • The first letter of each string is the same.
      • The first letter of each string is different.
    • For the first case, we solve the subproblem that removes the first letter from each, and add 1. In the grid, this subproblem is always the diagonal immediately down and right.

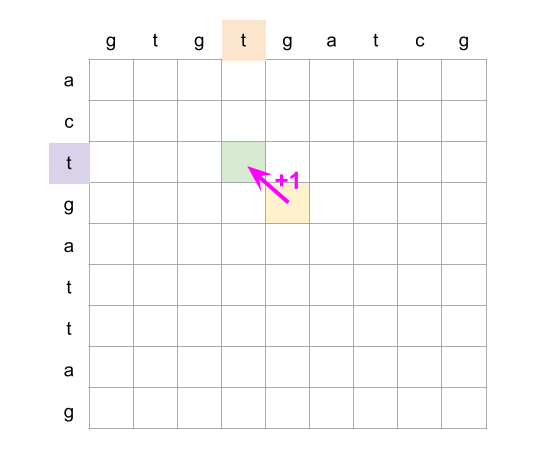
    • For the second case, we consider the subproblem that removes the first letter off the first word, and then the subproblem that removes the first letter off the second word. In the grid, these are subproblems immediately right and below.

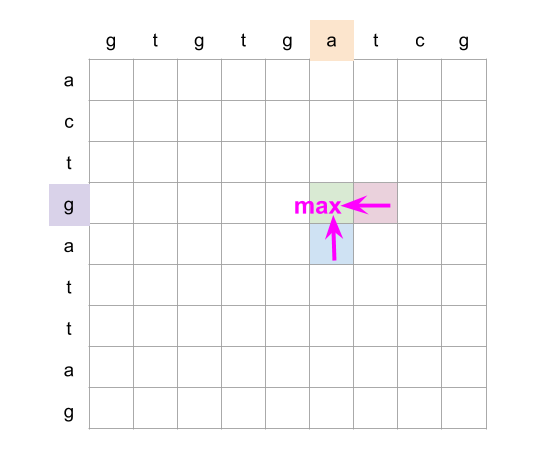
    • Putting this all together, we iterate over each column in reverse, starting from the last column (we could also do rows, the final result will be the same). For a cell (row, col), we look at whether or not text1.charAt(row) == text2.charAt(col) is true. if it is, then we set grid[row][col] = 1 + grid[row + 1][col + 1]. Otherwise, we set grid[row][col] = max(grid[row + 1][col], grid[row][col + 1]).
    • For ease of implementation, we add an extra row of zeroes at the bottom, and an extra column of zeroes to the right.
    • Here is an animation showing this algorithm.

Complexity
  • Time: \(O(M \cdot N)\)
    • We’re solving \(M \cdot N\) subproblems. Solving each subproblem is an \(O(1)\) operation.
  • Space: \(O(M \cdot N)\)
    • We’re allocating a 2D array of size \(M \cdot N\) to save the answers to subproblems.

Solution: Dynamic Programming with Space Optimization

  • Intuition:
    • You might have noticed in the Approach 3 animation that we only ever looked at the current column and the previous column. After that, previously computed columns are no longer needed (if you didn’t notice, go back and look at the animation).

      We can save a lot of space by instead of keeping track of an entire 2D array, only keeping track of the last two columns.

    • This reduces the space complexity to be proportional to the length of the word going down. We should make sure this is the shortest of the two words.

  • Algorithm:

      class Solution:
      def longestCommonSubsequence(self, text1: str, text2: str) -> int:
            
          # If text1 doesn't reference the shortest string, swap them.
          if len(text2) < len(text1):
              text1, text2 = text2, text1
            
            
          # The previous column starts with all 0's and like before is 1
          # more than the length of the first word.
          previous = [0] * (len(text1) + 1)
            
          # Iterate up each column, starting from the last one.
          for col in reversed(range(len(text2))):
              # Create a new array to represent the current column.
              current = [0] * (len(text1) + 1)
              for row in reversed(range(len(text1))):
                  if text2[col] == text1[row]:
                      current[row] = 1 + previous[row + 1]
                  else:
                      current[row] = max(previous[row], current[row + 1])
              # The current column becomes the previous one.
              previous = current
            
          # The original problem's answer is in previous[0]. Return it.
          return previous[0]
    • We can still do better!
    • One slight inefficiency in the above code is that a new current array is created on each loop cycle. While this doesn’t affect the space complexity—as we assume garbage collection happens immediately for the purposes of space complexity analysis—it does improve the actual time and space usage by a constant amount.
    • A couple of people have suggested that we could create current in the same place we create previous. Then each time, the current array will be reused. This, they argue, should work because we never modify the 0 at the end (the padding), and then, other than that 0, we’re only ever reading from indexes that we’ve already written to on that outer-loop iteration. This logic is entirely correct.
    • However, it will break for a different reason. The line previous = current makes both previous and current reference the same list. This happens at the end of the first loop cycle. So after that point, the algorithm is no longer functioning as intended.
    • There is another solution, though: notice that when we do previous = current, we are removing the reference to the previous array. At this point, it would normally be garbage collected. Instead, though, we could use that array as our current array for the next iteration! This way, we’re not making both variables reference the same array, and we’re reusing a no longer array instead of creating a new one. Correctness is guaranteed, as explained above, we’re only ever reading the 0 at the end or values we’ve already written to in that outer-loop iteration.
    • Here is the slightly modified code for your reference.
      class Solution:
      def longestCommonSubsequence(self, text1: str, text2: str) -> int:
            
          # If text1 doesn't reference the shortest string, swap them.
          if len(text2) < len(text1):
              text1, text2 = text2, text1
            
            
          # The previous and current column starts with all 0's and like 
          # before is 1 more than the length of the first word.
          previous = [0] * (len(text1) + 1)
          current = [0] * (len(text1) + 1)
            
          # Iterate up each column, starting from the last one.
          for col in reversed(range(len(text2))):
              for row in reversed(range(len(text1))):
                  if text2[col] == text1[row]:
                      current[row] = 1 + previous[row + 1]
                  else:
                      current[row] = max(previous[row], current[row + 1])
              # The current column becomes the previous one, and vice versa.
              previous, current = current, previous
            
          # The original problem's answer is in previous[0]. Return it.
          return previous[0]
Complexity
  • Time: \(O(M \cdot N)\), where \(M\) be the length of the first word, and \(N\) be the length of the second word.
    • Like before, we’re solving \(M \cdot N\) subproblems, and each is an \(O(1)\) operation to solve.
  • Space: \(O(\min(M, N))\)
    • We’ve reduced the auxilary space required so that we only use two 1D arrays at a time; each the length of the shortest input word. Seeing as the 2 is a constant, we drop it, leaving us with the minimum length out of the two words.

[1531/Hard] String Compression II

Problem

  • Run-length encoding is a string compression method that works by replacing consecutive identical characters (repeated 2 or more times) with the concatenation of the character and the number marking the count of the characters (length of the run). For example, to compress the string "aabccc" we replace "aa" by "a2" and replace "ccc" by "c3". Thus the compressed string becomes "a2bc3".
  • Notice that in this problem, we are not adding '1' after single characters.
  • Given a string s and an integer k. You need to delete at most k characters from s such that the run-length encoded version of s has minimum length.

  • Find the minimum length of the run-length encoded version of s after deleting at most k characters.

  • Example 1:
Input: s = "aaabcccd", k = 2
Output: 4
Explanation: Compressing s without deleting anything will give us "a3bc3d" of length 6. Deleting any of the characters 'a' or 'c' would at most decrease the length of the compressed string to 5, for instance delete 2 'a' then we will have s = "abcccd" which compressed is abc3d. Therefore, the optimal way is to delete 'b' and 'd', then the compressed version of s will be "a3c3" of length 4.
  • Example 2:
Input: s = "aabbaa", k = 2
Output: 2
Explanation: If we delete both 'b' characters, the resulting compressed string would be "a4" of length 2.
  • Example 3:
Input: s = "aaaaaaaaaaa", k = 0
Output: 3
Explanation: Since k is zero, we cannot delete anything. The compressed string is "a11" of length 3.
  • Constraints:
    • 1 <= s.length <= 100
    • 0 <= k <= s.length
    • s contains only lowercase English letters.
  • See problem on LeetCode.

Solution

  • Two ideas:

    • Each group of repeated characters can be shortened only to no characters, one character, 9 character, or 99 characters. All other options either do not decrease the group code or consume extra available deletions.
    • If there are some characters between two groups of the same character (e.g., “bg” in “aabga”), then a shorter coded sequence can be formed by dropping the intermediate part and by merging the surrounding groups of the same character (e.g., "aabga" with dropped 2 characters -> "a3").

  • Pre-processing:

    • Form (1) string chars that holds group characters and (2) list frequency that holds frequencies of these characters within the groups. For string "aabbbca", the string will be "abca" and the list will be [2, 3, 1, 1].
    • Create table dynamic that storeы the results of the function to avoid repeated calculations. The table will be indexed by the group number (in string chars) and the number of available deletions.

  • Function FindMinLen:

    • Along with the input ind of character group index and input res_k of available deletions, we keep track of carry-overs from the previous group of same characters. Please see comments within the function.
    • The function calculates the smallest code length if we start with group ind and have res_k deletions. The function can account for carry_over number of characters that are added to the current group of characters.
    • Example of function usage. String is "aaacgbbaaf", de-duplicated string is "acgbaf", frequency list is [3, 1, 1, 2, 2, 1].
    • Function call FindMinLen(4, 2, carry_over=3) will calculate min code if we start with group 4 (remaining string "aaf"), have 2 deletions, and group 4 needs to be increased by 3 characters as if we have string "aaaaaf".
class Solution:
    def getLengthOfOptimalCompression(self, s: str, k: int) -> int:
        # Find min lenth of the code starting from group ind, if there are res_k characters to delete and 
        # group ind needs to be increased by carry_over additional characters
        def FindMinLen(ind, res_k, carry_over=0): 
            
            # If we already found the min length - just retrieve it (-1 means we did not calculate it)
            if carry_over == 0 and dynamic[ind][res_k] != -1:
                return dynamic[ind][res_k]
            
            # Number of character occurrences that we need to code. Includes carry-over.
            cur_count = carry_over + frequency[ind]

            # Min code length if the group ind stays intact. The code accounts for single-character "s0" vs. "s"  situation.
            min_len = 1 + min(len(str(cur_count)), cur_count - 1) + FindMinLen(ind+1,res_k)

            # Min length if we keep only 0, 1, 9, or 99 characters in the group - delete the rest, if feasible
            for leave_count, code_count in [(0,0), (1, 1), (9, 2), (99, 3)]:
                if cur_count > leave_count and res_k >= cur_count - leave_count:
                    min_len = min(min_len, code_count + FindMinLen(ind + 1,res_k - (cur_count - leave_count)))

            # If we drop characters between this character group and next group, like drop "a" in "bbbabb"
            next_ind = chars.find(chars[ind], ind + 1)
            delete_count = sum(frequency[ind+1:next_ind])
            if next_ind > 0 and res_k >= delete_count:
                min_len = min(min_len, FindMinLen(next_ind, res_k - delete_count, carry_over = cur_count))

            # If there was no carry-over, store the result
            if carry_over == 0: dynamic[ind][res_k] = min_len
            return min_len
        
        # Two auxiliary lists - character groups (drop repeated) and number of characters in the group
        frequency, chars = [], ""
        for char in s:
            if len(frequency)==0 or char != chars[-1]:
                frequency.append(0)
                chars = chars + char
            frequency[-1] += 1
        
        # Table with the results. Number of character groups by number of available deletions.  
        dynamic = [[-1] * (k + 1) for i in range(len(frequency))] + [[0]*(k + 1)]
        
        return FindMinLen(0, k)

Famous DP Problems

Further Reading

Quiz

  • Sample Quiz to test your knowledge.