• This section introduces one specific application of Binary Search, i.e., when you are asked to find the upper or lower bound, or more precisely, when you need to find the maximum of the smallest value or the minimum of the largest value. Binary Search is an algorithm to search for a target from a sorted array. It selects the middle element in the array and compares it against the target; if they are not equal, it eliminates one half of the array and keeps searching the other half in the same manner (Wikipedia).
  • The most basic application of it is to find a number or a position from an array. Some practices could be found on Leetcode:
    • First Bad Version
    • Search in Rotated Sorted Array
    • Find First and Last Position of Element in Sorted Array
    • Median of Two Sorted Arrays
  • Another popular case to apply is when you are asked to find the maximum of the smallest value or the minimum of the largest value. Let’s take Split Array Largest Sum as an example to illustrate how to deal with this kind of problem.
  • Search space:
    • The search space would be from the maximum of the input nums, when m=len(nums), to the sum of nums, when m=1.
  • Search strategy:
    • Each time we would pick the middle element mid of the search space as our threshold, and calculate the number of subarrays count while making sure that the sum of each subarray does not exceed mid. If count>m, it means we should increase mid to reduce the number of subarrays; else if count<=m, it means we can decrease mid to increase the number of subarrays, but mid is still qualified.
    • The following image shows the steps to apply binary search:

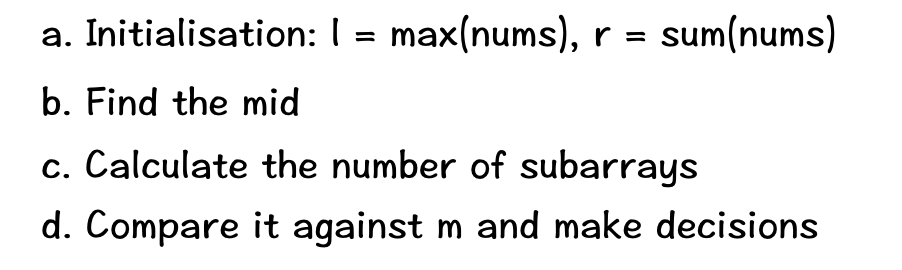
    • So the pseudocode is:
      while l < r:
      mid = l + (r-l)//2
        
      if count(mid) > m:
          l = mid + 1
      else:
          r = mid
            
  return l
  • Picking mid:
    • When picking the mid out of odd number of items, we can find the middle one; when the number of items is even, there are two ways to pick: the former one or the latter one.
    • Pick the former one or the latter one out of an even number of items:

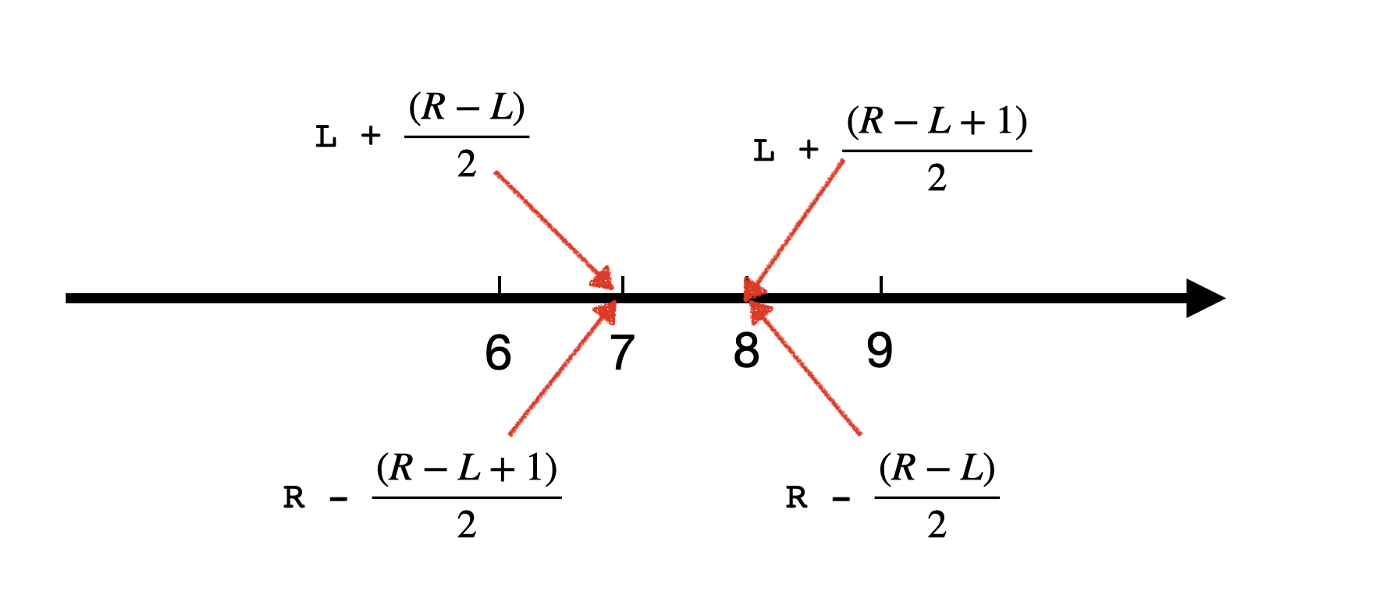
    • Both of them works, but it should align with how we deal with l and r. When we select the former one using l+(r-l)/2, we want to make sure to avoid l = mid because that might lead to infinite loop. For example when there are two elements [0,1] and mid=0, then l becomes mid and the iteration goes again and again.
    • Similarly, when we select the latter one using r-(r-l)/2, we want to avoid r=mid.

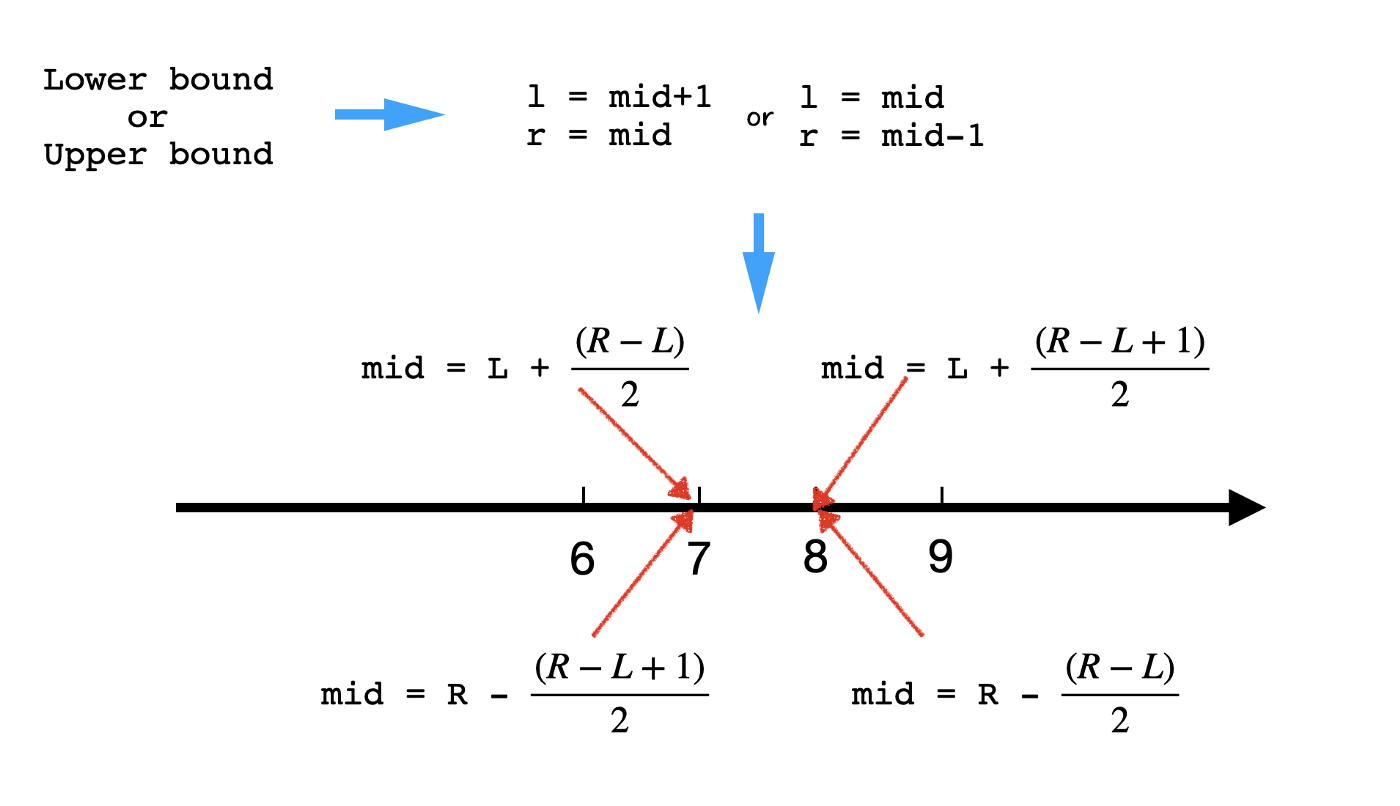
  • Picking l and r:

    • Depends on the context!
      • Lower bound
        • For example, when the question asks for the lower bound, if mid works, then r should be mid not mid-1 because mid might be the answer! And when mid does not work, l should be mid+1 because we are sure the mid is not the answer and everything that falls one mid‘s left won’t work either.

      • Upper bound
        • Similarly, we can assign values to l and r as below.

    • Overall, the way we select mid and assign values to l and r is determined by which we are looking for: lower bound vs. upper bound.
  • How to choose mid, l, and r:

[33/Medium] Search in Rotated Sorted Array

  • There is an integer array nums sorted in ascending order (with distinct values).

  • Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

  • Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

  • You must write an algorithm with O(log n) runtime complexity.

  • Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
  • Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
  • Example 3:
Input: nums = [1], target = 0
Output: -1
  • Constraints:
    • 1 <= nums.length <= 5000
    • -104 <= nums[i] <= 104
    • All values of nums are unique.
    • nums is an ascending array that is possibly rotated.
    • -104 <= target <= 104
  • See problem on LeetCode.
  • Background:
    • We have an ascending array, which is rotated at some pivot. Let’s call the rotation the inflection point (IP).
    • One characteristic the inflection point holds is: arr[IP] > arr[IP + 1] and arr[IP] > arr[IP - 1].
    • If we rotated an array [0, 1, 2, 3, 4, 7, 8, 9] to [7, 8, 9, 0, 1, 2, 3, 4], the inflection point (where the numbers go from monotonically increasing to decreasing or vice-versa), IP number 9 (in terms of the pivot , this would be index 5).
    • One thing we can see is that values until the IP are ascending. And values from IP + 1 until end are also ascending (hint: binary search).
    • Also the values from [0, IP] are always bigger than [IP + 1, n].
  • Intuition:
    • We can perform a Binary Search.
    • If A[mid] is bigger than A[left] we know the inflection point will be to the right of us, meaning values from a[left] ... a[mid] are ascending.
    • So if target is between that range we just cut our search space to the left. Otherwise go right.
    • The other condition is that A[mid] is not bigger than A[left] meaning a[mid] ... a[right] is ascending.
    • In the same manner we can check if target is in that range and cut the search space correspondingly.
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if not nums:
            return -1

        low, high = 0, len(nums) - 1

        while low <= high:
            mid = (low + high) // 2
            if target == nums[mid]:
                return mid

            # left portion is sorted, i.e., left is strictly increasing.
            # inflection point to the right of mid.
            if nums[low] <= nums[mid]:
                if nums[low] <= target <= nums[mid]:
                    high = mid - 1
                else:
                    low = mid + 1

            # left portion is unsorted, i.e., right is strictly increasing.
            # inflection point to the left of mid.
            else:
                if nums[mid] <= target <= nums[high]:
                    low = mid + 1
                else:
                    high = mid - 1

        return -1
Complexity
  • Time: \(O(\log{n})\) where \(n\) is \(len(nums)\)
  • Space: \(O(1)\)

[34/Medium] Find First and Last Position of Element in Sorted Array

  • Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.

  • If target is not found in the array, return [-1, -1].

  • You must write an algorithm with O(log n) runtime complexity.

  • Example 1:

Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
  • Example 2:
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
  • Example 3:
Input: nums = [], target = 0
Output: [-1,-1]
  • Constraints:
    • 0 <= nums.length <= 105
    • -109 <= nums[i] <= 109
    • nums is a non-decreasing array.
    • -109 <= target <= 109
  • See problem on LeetCode.

Solution: Binary Search

  • Explanation:
    • search(): 
        find the lowest index of target num in nums
  if there is target num in nums
      lo = lowest index of target
      hi = lowest index of target
  if there is no target num in nums
      if there is higher num than target in nums
          lo = lowest index of the first higher num than target in nums
          hi = lowest index of the first higher num than target in nums
      if there is no higher num than target in nums
          lo = len(nums)
          hi = len(nums)
    • after lo = search(target), hi = search(target+1)-1: 
        if there is more than one target num
      lo = lowest index of target
      hi = (lowest index of the first higher num than target)-1 (highest index of target)
      then, lo < high
  elif there is only one target num
      lo == high
  else
      if there is only higher number than target in nums
          lo = lowest index of the first higher num than target (at least target+1 or higher)
          hi = lowest index of the (target+1) - 1
          then, lo > high
      if there is only lower number than target in nums
          lo = len(nums)
          hi = len(nums)-1
          then, lo > high

def searchRange(self, nums, target):
    def binarySearchLeft(A, x):
        left, right = 0, len(A) - 1
        while left <= right:
            mid = (left + right) / 2
            if x > A[mid]: left = mid + 1
            else: right = mid - 1
        return left

    def binarySearchRight(A, x):
        left, right = 0, len(A) - 1
        while left <= right:
            mid = (left + right) / 2
            if x >= A[mid]: left = mid + 1
            else: right = mid - 1
        return right
        
    left, right = binarySearchLeft(nums, target), binarySearchRight(nums, target)
    return (left, right) if left <= right else [-1, -1]
  • Same approach; compressed version:
class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        def search(x):
            lo, hi = 0, len(nums)           
            while lo < hi:
                mid = (lo + hi) // 2
                if nums[mid] < x:
                    lo = mid+1
                else:
                    hi = mid                    
            return lo
        
        lo = search(target)
        hi = search(target + 1)-1
        
        return [lo, hi] if lo <= hi else [-1, -1]
Complexity
  • Time: \(O(\log{n})\)
  • Space: \(O(1)\)

[162/Medium] Find Peak Element

Problem

  • A peak element is an element that is strictly greater than its neighbors.

  • Given an integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.

  • You may imagine that nums[-1] = nums[n] = -∞.

  • You must write an algorithm that runs in O(log n) time.

  • Example 1:

Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.
  • Example 2:
Input: nums = [1,2,1,3,5,6,4]
Output: 5
Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
  • Constraints:
    • 1 <= nums.length <= 1000
    • -2^31 <= nums[i] <= 2^31 - 1
    • nums[i] != nums[i + 1] for all valid i.
  • See problem on LeetCode.

Solution: Binary search

class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        left = 0
        right = len(nums)-1

        # handle condition 3
        while left < right-1:
            mid = (left+right) // 2
            if nums[mid] > nums[mid+1] and nums[mid] > nums[mid-1]:
                return mid

            if nums[mid] < nums[mid+1]:
                left = mid+1
            else:
                right = mid-1

        # handle condition 1 and 2
        return left if nums[left] >= nums[right] else right
Complexity
  • Time: \(O(\log{n})\)
  • Space: \(O(1)\)

Solution: One-liner

class Solution:
    # @param nums, an integer[]
    # @return an integer
    def findPeakElement(self, nums):
        return nums.index(max(nums))
Complexity
  • Time: \(O(n)\)
  • Space: \(O(1)\)

[278/Easy] First Bad Version

Problem

  • You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
  • Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad.

  • You are given an API bool isBadVersion(version) which returns whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.

  • Example 1:
Input: n = 5, bad = 4
Output: 4
Explanation:
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
  • Example 2:
Input: n = 1, bad = 1
Output: 1
  • Constraints:
    • 1 <= bad <= n <= 2^31 - 1
  • See problem on LeetCode.

Solution: Binary search

# The isBadVersion API is already defined for you.
# def isBadVersion(version: int) -> bool:

class Solution:
    def firstBadVersion(self, n: int) -> int:
        """
        :type n: int
        :rtype: int
        """
        
        r = n-1
        l = 0
        
        while l <= r:
            mid = l + (r-l)//2 # or (l + r)//2
            if not isBadVersion(mid):
                l = mid+1
            else:
                r = mid-1
                
        # returning left here because we need the first bad version
        return l
Complexity
  • Time: \(O(\log{n})\)
  • Space: \(O(1)\)

Solution: Bisect

# The isBadVersion API is already defined for you.
# def isBadVersion(version: int) -> bool:

import bisect

class Solution(dict):
    def firstBadVersion(self, n: int) -> int:
        return bisect.bisect_left(self, True, 1, n)
    
    def __getitem__(self, key):
        return isBadVersion(key)
Complexity
  • Time: \(O(\log{n})\)
  • Space: \(O(1)\)

[362/Medium] Design Hit Counter

Problem

  • Design a hit counter which counts the number of hits received in the past 5 minutes (i.e., the past 300 seconds).

  • Your system should accept a timestamp parameter (in seconds granularity), and you may assume that calls are being made to the system in chronological order (i.e., timestamp is monotonically increasing). Several hits may arrive roughly at the same time.

  • Implement the HitCounter class:
    • HitCounter() Initializes the object of the hit counter system.
    • void hit(int timestamp) Records a hit that happened at timestamp (in seconds). Several hits may happen at the same timestamp.
    • int getHits(int timestamp) Returns the number of hits in the past 5 minutes from timestamp (i.e., the past 300 seconds).
  • Example 1:
Input
["HitCounter", "hit", "hit", "hit", "getHits", "hit", "getHits", "getHits"]
[[], [1], [2], [3], [4], [300], [300], [301]]
  • Output
[null, null, null, null, 3, null, 4, 3]

Explanation
HitCounter hitCounter = new HitCounter();
hitCounter.hit(1);       // hit at timestamp 1.
hitCounter.hit(2);       // hit at timestamp 2.
hitCounter.hit(3);       // hit at timestamp 3.
hitCounter.getHits(4);   // get hits at timestamp 4, return 3.
hitCounter.hit(300);     // hit at timestamp 300.
hitCounter.getHits(300); // get hits at timestamp 300, return 4.
hitCounter.getHits(301); // get hits at timestamp 301, return 3.
  • Constraints:
    • 1 <= timestamp <= 2 * 109
    • All the calls are being made to the system in chronological order (i.e., timestamp is monotonically increasing).
    • At most 300 calls will be made to hit and getHits.
  • See problem on LeetCode.

Solution: Deque

class HitCounter(object):

def __init__(self):
    """
    Initialize your data structure here.
    """
    from collections import deque
    
    self.num_of_hits = 0
    self.time_hits = deque()
    

def hit(self, timestamp):
    """
    Record a hit.
    @param timestamp - The current timestamp (in seconds granularity).
    :type timestamp: int
    :rtype: void
    """
    if not self.time_hits or self.time_hits[-1][0] != timestamp:
        self.time_hits.append([timestamp, 1])
    else:
        self.time_hits[-1][1] += 1
    
    self.num_of_hits += 1
            
    

def getHits(self, timestamp):
    """
    Return the number of hits in the past 5 minutes.
    @param timestamp - The current timestamp (in seconds granularity).
    :type timestamp: int
    :rtype: int
    """
    while self.time_hits and self.time_hits[0][0] <= timestamp - 300:
        self.num_of_hits -= self.time_hits.popleft()[1]
    
    return self.num_of_hits
Complexity
  • Time: \(O(\log{n})\)
  • Space: \(O(1)\)

Solution: Binary Search

  • Two step process:
    1. Add each timestamp in a list for hit().
    2. For each timestamp in getHits(), find the index that (timestamp-300) would be inserted at (rightmost index that is) using binary search. The difference of current length of the timestamps list and that index would be the answer.
  • Why rightmost index?
    • See the following example:
      • If values(timestamps) = [1,301], and we look to do getHits(301), we would try and find where (301-300)=1 should be inserted. If we’re looking for the left most value, the index would be 0 and the ans would len(values)-idx = 2-0 = 2, which is wrong for the questions’ constraints.
      • The timestamp 5 minutes is a hard bounds, which means if we go back 300 seconds for time 301, the 1s is actually the 301st second, which puts it outside our bound.
      • So, we would actually find the rightmost index where this value should be inserted at as that would be a value, that is within our bounds.
    • So going through the example above, when we find the rightmost idx to insert 1 at in [1,301], we would get 1, and the answer would len(values)-idx = 2-1 = 1.
  • Intuition:
    • Store the incoming timestamps in an array.
    • Timestamps are monotonically increasing, so the resulting array will be sorted in increasing order. Once you’d like to get the number of hits within the last 300 seconds, find the cutoff index at timestamp - 300 in the sorted array.
    • The timestamps to the right of this cutoff occurred within the 300 seconds.
    • The length of the array minus the cutoff index gives you the count of these timestamps within 300 seconds. Done!
  • Note the benefit of keeping all recorded hits:
    • Other solutions argue for a queue where all the timestamps with difference greater than or equal to 300 are removed from the queue. This approach is not favorable in a real-world context.
    • From a design perspective, it os better to present an extendable solution that is able to run more summary statistics (e.g hits in last 15 minutes, average hits, etc.). Once you’ve removed the hits from your queue, these will be impossible to calculate (except you’ve stored them somewhere beyond the machines memory).
  • Using inbuilt bisect library:
(Using inbuilt bisect library) 32ms:

class HitCounter:

    def __init__(self):
        self.values = []

    def hit(self, timestamp: int) -> None:
        self.values.append(timestamp)

    def getHits(self, timestamp: int) -> int:
        right = len(self.values)
        left = bisect.bisect_right(self.values, timestamp-300)
        return right-left
  • Implementing Binary Search for Rightmost Value:
class HitCounter:

    def __init__(self):
        self.values = []

    def hit(self, timestamp: int) -> None:
        self.values.append(timestamp)
        
    def __findIdx(self, target):
        l = 0
        r = len(self.values)
        
        while l < r:
            m = (l + r) // 2
            if self.values[m] > target:
                r = m
            else:
                l = m + 1
        return l                     

    def getHits(self, timestamp: int) -> int:
        right = len(self.values)
        left = self.__findIdx(timestamp-  300)
        return right-left
Complexity
  • Let n be the number of times hit(). Alternatively, its the number of timestamps inserted in the list.
  • Time:
    • hit() -> O(1).
    • getHits() -> O(logn).
  • Space: \(O(n)\)

[410/Hard] Split Array Largest Sum

Problem

  • Given an array nums which consists of non-negative integers and an integer m, you can split the array into m non-empty continuous subarrays.

  • Write an algorithm to minimize the largest sum among these m subarrays.

  • Example 1:

Input: nums = [7,2,5,10,8], m = 2
Output: 18
Explanation:
There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8],
where the largest sum among the two subarrays is only 18.
  • Example 2:
Input: nums = [1,2,3,4,5], m = 2
Output: 9
  • Example 3:
Input: nums = [1,4,4], m = 3
Output: 4
  • Constraints:
    • 1 <= nums.length <= 1000
    • 0 <= nums[i] <= 106
    • 1 <= m <= min(50, nums.length)
  • See problem on LeetCode.

Solution: Binary Search

class Solution:
    def splitArray(self, nums: List[int], m: int) -> int:
        """
        :type nums: List[int]
        :type m: int
        :rtype: int
        """
        def split(nums, largest_sum):
            """
            Given the largest_sum returns the number of pieces.
            """
            pieces = 1
            tmp_sum = 0
            for num in nums:
                if tmp_sum + num > largest_sum:
                    tmp_sum = num
                    pieces += 1
                else:
                    tmp_sum += num
            return pieces
        
        # pieces is number of pieces for a given largest_sum
        # For pieces = len(nums), the largest_sum is max(nums)
        # for pieces = 1, the largest_sum is sum(nums)
        # We are looking for p=m, as we go from p=1 to p=len(nums) the 
        # largest sum goes from max(nums) to sum(nums) (which is our search space)
        low = max(nums)  # m = len(nums)
        high = sum(nums) # m = 1
        # if pieces > m high is small
        while low < high:
            mid = (low + high) // 2 # or mid = low + (high - low) // 2
            pieces = split(nums, mid)
            if pieces > m: # the largest_sum is small, we have too many pieces and we can merge some of them
                # we have more pieces than m, which means largest sum needs to increase so set low to mid+1
                low = mid + 1
            else:
                # mid works so cap high to mid
                high = mid 
        return low
Complexity
  • Time: \(O(n\log{m})\) where \(m = sum(nums)\) and \(nums\) is the input array containing \(n\) items.
  • Space \(O(1)\)

[528/Medium] Random Pick with Weight

Problem

  • You are given a 0-indexed array of positive integers w where w[i] describes the weight of the i^th index.

  • You need to implement the function pickIndex(), which randomly picks an index in the range [0, w.length - 1] (inclusive) and returns it. The probability of picking an index i is w[i] / sum(w).

    • For example, if w = [1, 3], the probability of picking index 0 is 1 / (1 + 3) = 0.25 (i.e., 25%), and the probability of picking index 1 is 3 / (1 + 3) = 0.75 (i.e., 75%).

  • Example 1:

Input
["Solution","pickIndex"]
[[[1]],[]]
Output
[null,0]
Explanation
Solution solution = new Solution([1]);
solution.pickIndex(); // return 0. The only option is to return 0 since there is only one element in w.
  • Example 2:
Input
["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
[[[1,3]],[],[],[],[],[]]
Output
[null,1,1,1,1,0]
Explanation
Solution solution = new Solution([1, 3]);
solution.pickIndex(); // return 1. It is returning the second element (index = 1) that has a probability of 3/4.
solution.pickIndex(); // return 1
solution.pickIndex(); // return 1
solution.pickIndex(); // return 1
solution.pickIndex(); // return 0. It is returning the first element (index = 0) that has a probability of 1/4.

Since this is a randomization problem, multiple answers are allowed.
All of the following outputs can be considered correct:
[null,1,1,1,1,0]
[null,1,1,1,1,1]
[null,1,1,1,0,0]
[null,1,1,1,0,1]
[null,1,0,1,0,0]
......
and so on.
  • Constraints:
    • 1 <= w.length <= 104
    • 1 <= w[i] <= 105
    • pickIndex will be called at most 104 times.
  • See problem on LeetCode.

Solution: Normalize weights, sample N uniformly and pick based on testing if N <= Weight

  1. Normalize the weights in the initial w list to ratios
    1. i.e., [1, 3, 3, 1] --> [1 / 8, 3 / 8, 3 / 8, 1 / 8], for a general list […i…] —> [… i / sum(list) …]
    2. This give us the frequency of each index
  2. Take these new weights and put them on a number line from 0 –> 1 by adding to each element all of the previous elements
    1. i.e. [1/8, 3/8, 3/8, 1/8] –> [1/8,4/8,7/8,1], for a general list […i…] —> [… i + sum(all previous)…]
    2. Note this will always mean list[-1] = 1
    3. This gives us a number line to test a random variable on
  3. Generate a random number between 0, 1
  4. Find the section of the number line the random number falls into and return its index
    1. The while loop effectively gives us each index with its correct probability
Pseudocode:
1. Initialize class.
2. Get a list of all unique values.
3. Normalize weights.
4. Put weights on the number line.
5. If a uniform variable falls in the range of a value that value is returned.

import random

class Solution:
    def __init__(self, w: List[int]):
        self.w = w
        # 1. calculate relative frequency
        denom = sum(self.w)
        
        for i in range(len(self.w)):
            self.w[i] = self.w[i] / denom
            
        # 2. put relative frequencies on the number line between 0 and 1
        # Note self.w[-1] = 1
        for i in range(1, len(self.w)):
            self.w[i] += self.w[i-1]
        
    def pickIndex(self) -> int:
        # this is where we pick the index
        N = random.uniform(0, 1)
        
        # test each region of the number line to see if N falls in it, if it 
        # does not then go to the next index and check if N falls in it
        # this is guaranteed to break because of previous normalization
        for index, weight in enumerate(self.w):
            if N <= weight:
                return index
        
        # OR
        # index = 0
        # while index < len(self.w):
        #     if N <= self.w[index]:
        #         return index
        #     index += 1
        
        # OR    
        # flag = 1
        # index = -1
        # 
        # while flag:
        #     index +=1 
        #     if N <= self.w[index]:
        #         flag = 0
        #         
        # return index

Solution: Binary search

class Solution:

    def __init__(self, w: List[int]):
        s = sum(w)
        self.weight = [w[0]/s]
        for i in range(1, len(w)):            
            self.weight.append(self.weight[-1]+w[i]/s)

    def pickIndex(self) -> int:
        l, r, seed = 0, len(self.weight)-1, random.random()
        while l < r:
            m = (l+r)//2
            if self.weight[m] <= seed: l = m+1
            else: r = m
        return l
Complexity
  • Time: \(O(n + n) = O(2n) = O(n)\)
  • Space: \(O(1)\)

[774/Hard] Minimize Max Distance to Gas Station

Problem

  • You are given an integer array stations that represents the positions of the gas stations on the x-axis. You are also given an integer k.

  • You should add k new gas stations. You can add the stations anywhere on the x-axis, and not necessarily on an integer position.

  • Let penalty() be the maximum distance between adjacent gas stations after adding the k new stations.

  • Return the smallest possible value of penalty(). Answers within 10-6 of the actual answer will be accepted.

  • Example 1:

Input: stations = [1,2,3,4,5,6,7,8,9,10], k = 9
Output: 0.50000
  • Example 2:
Input: stations = [23,24,36,39,46,56,57,65,84,98], k = 1
Output: 14.00000
  • Constraints:
    • 10 <= stations.length <= 2000
    • 0 <= stations[i] <= 108
    • stations is sorted in a strictly increasing order.
    • 1 <= k <= 106
  • See problem on LeetCode.

Solution: Binary Search

  • The hint is that “answers within 10^-6 of the true value will be accepted as correct”. Because binary search may not find exact value but it can approach the correct answer.
  • To use binary search to find the smallest possible value of penalty distance, initialize left = 0 and right = the distance between the first and the last station. count is the number of gas station we need to make it possible.
  • if count > k, it means mid is too small to realize using k stations.
  • if count <= k, it means mid is possible and we can continue to find a bigger one.
  • When left + 1e-6 >= right, it means that the answer is within 10^-6 of the true value.
class Solution:
    def minmaxGasDist(self, stations: List[int], k: int) -> float:
        left, right = 1e-6, stations[-1] - stations[0]
        
        while left + 1e-6 < right:
            mid = (left + right) / 2
            count = 0
            for a, b in zip(stations, stations[1:]):
                count += math.ceil((b - a) / mid) - 1
            if count > k:
                left = mid
            else:
                right = mid
                
        return right
Complexity
  • Time: \(O(n\log{m})\) where \(m = stations[N - 1] - stations[0]\) and \(stations\) is the input array containing \(n\) items.
  • Space \(O(1)\)

[825/Medium] Friends Of Appropriate Ages

Problem

  • There are n persons on a social media website. You are given an integer array ages where ages[i] is the age of the i-th person.

  • A person x will not send a friend request to a person y (x != y) if any of the following conditions is true:

    • age[y] <= 0.5 * age[x] + 7
    • age[y] > age[x]
    • age[y] > 100 && age[x] < 100

  • Otherwise, x will send a friend request to y.

  • Note that if x sends a request to y, y will not necessarily send a request to x. Also, a person will not send a friend request to themselves.

  • Return the total number of friend requests made.

  • Example 1:

Input: ages = [16,16]
Output: 2
Explanation: 2 people friend request each other.
  • Example 2:
Input: ages = [16,17,18]
Output: 2
Explanation: Friend requests are made 17 -> 16, 18 -> 17.
  • Example 3:
Input: ages = [20,30,100,110,120]
Output: 3
Explanation: Friend requests are made 110 -> 100, 120 -> 110, 120 -> 100.
  • Constraints:
    • n == ages.length
    • 1 <= n <= 2 * 104
    • 1 <= ages[i] <= 120
  • See problem on LeetCode.
Complexity
  • Time: \(O(\log{n})\)
  • Space: \(O(n)\)

Solution: Dictionary with {age: num_members}, iterate for each age group and check conditions

  • Algorithm:
    • Step 1: construct a dictionary with age as key and number of members in that age group as values. This can be done using Counter in the collections module.
    • Step 2: iterate for every age group (not every person!) say “me”
    • Step 3: for every age group check condition take (“age”,”me”) pair and check if the conditions asked are satisfied with
      age<= 0.5 * me +7
  age>me
  3rd condition is always false so we can omit it.
    • Step 4:
      • Here we have 2 cases.
      • Case (a): if your age is different from the other age
        • For e.g., 16, 15, 15 then 15->16 and 15->16, i.e., 2*1 which is age_count * me_count
      • Case (b): if your age is same as other age
        • For e.g., 16, 16 then 16<->16 i.e., 2.
        • This would be same as number of edges in a graph with n vertices where each edge considered 2 times which is 2*nC2 which would be me_count*(me_count-1)
from collections import Counter
class Solution:
    def numFriendRequests(self, ages: List[int]) -> int:
        count = 0
        # Step 1
        ages_dict = Counter(ages)
        
        # Step 2
        for me in ages_dict:
            my_age_count = ages_dict[me]
            # Step 3
            for age in ages_dict:
                if not (age <= 0.5 * me + 7 or age > me):
                    # Step 4: case (a)
                    if age != me:
                        count += ages_dict[age]*my_age_count
                    # Step 4: case (b)
                    else:
                        count += int(my_age_count*(my_age_count-1))
        
        return count
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

Solution: Binary Search with Counter

  • Algorithm:
    1. Sort by age
    2. index i person will not send friend request to ages[i]+1, ages[i]+2 ….
    3. index i person will not send friend request to elements whose age is less than (0.5 * ages[i] + 7)
    4. Using binary search we can find upper and lower limit, persons which fall in this range, can send friend requests (remove 1, i-th person itself)
import bisect
from collections import Counter

class Solution:
    def numFriendRequests(self, ages: List[int]) -> int:
        ages.sort()
        counts = Counter(ages)
        total = 0

        for age in counts:
            min_age = 0.5 * age + 7 # or age / 2 + 7
            left = bisect.bisect_right(ages, min_age)
            right = bisect.bisect_right(ages, age)
            total += max(0, right - left - 1)*counts[age] # you cannot have negative count

        return total
Complexity
  • Time: \(O(n)\)
  • Space: \(O(n)\)

Solution: Binary Search without a Counter

import bisect
from collections import Counter

class Solution:
    def numFriendRequests(self, ages: List[int]) -> int:
        ages.sort()
        count = 0
        
        for age in ages:
            left = bisect.bisect_right(ages, (0.5 * age) + 7)
            right = bisect.bisect_right(ages, age)
            count += max(0, right - left - 1) # you cannot have negative count
        return count
Complexity
  • Time: \(O(n)\)
  • Space: \(O(1)\)

[875/Medium] Koko Eating Bananas

Problem

  • Koko loves to eat bananas. There are n piles of bananas, the i-th pile has piles[i] bananas. The guards have gone and will come back in h hours.

  • Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.

  • Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.

  • Return the minimum integer k such that she can eat all the bananas within h hours.

  • Example 1:

Input: piles = [3,6,7,11], h = 8
Output: 4
  • Example 2:
Input: piles = [30,11,23,4,20], h = 5
Output: 30
  • Example 3:
Input: piles = [30,11,23,4,20], h = 6
Output: 23
  • Constraints:
    • 1 <= piles.length <= 104
    • piles.length <= h <= 109
    • 1 <= piles[i] <= 109
  • See problem on LeetCode.

Solution: Binary search

  • Binary search between [1, max(piles)] to find the result.
  • Note that ceil(p / m) is equal to (p + m - 1) // m.
class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:
        # bananas-per-hour rate can vary between 1 and max(piles)
        l, r = 1, max(piles)
        
        while l < r:
            m = (l + r) // 2
            # the ceil is present because if pile has less than `k` bananas, 
            # Koko eats all of them instead and will not eat any more bananas during this hour.
            if sum(ceil(num_bananas_in_pile / m) for num_bananas_in_pile in piles) > h:
                # the number of hours needed are beyond what's permissible, i.e., the bananas-per-hour rate is less than needed
                l = m + 1
            else:
                r = m
                
        return l
Complexity
  • Time: \(O(n\log{m})\) where \(m = max(piles)\) and \(piles\) is the input array containing \(n\) items.
  • Space \(O(1)\)

[1011/Medium] Capacity To Ship Packages Within D Days

Problem

  • A conveyor belt has packages that must be shipped from one port to another within days days.

  • The i-th package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.

  • Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within days days.

  • Example 1:

Input: weights = [1,2,3,4,5,6,7,8,9,10], days = 5
Output: 15
Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10

Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.
  • Example 2:
Input: weights = [3,2,2,4,1,4], days = 3
Output: 6
Explanation: A ship capacity of 6 is the minimum to ship all the packages in 3 days like this:
1st day: 3, 2
2nd day: 2, 4
3rd day: 1, 4
  • Example 3:
Input: weights = [1,2,3,1,1], days = 4
Output: 3
Explanation:
1st day: 1
2nd day: 2
3rd day: 3
4th day: 1, 1
  • Constraints:
    • 1 <= days <= weights.length <= 5 * 104
    • 1 <= weights[i] <= 500

Solution: Binary Search

  • Binary search doesn’t sound like a natural fit when this problem is first encountered. We might want to automatically treat weights as search space and then realize we’ve entered a dead end after wasting lots of time. In fact, we are looking for the minimal one among all feasible capacities.
  • The underpinning idea behind this problem is that if we can successfully ship all packages within D days with capacity m, then we can definitely ship them all with any capacity larger than m. Now we can design a condition function, let’s call it feasible, given an input capacity, it returns whether it’s possible to ship all packages within D days. This can run in a greedy way: if there’s still room for the current package, we put this package onto the conveyor belt, otherwise we wait for the next day to place this package. If the total days needed exceeds D, we return False, otherwise we return True.
  • Next, we need to initialize our boundary correctly. Obviously capacity should be at least max(weights), otherwise the conveyor belt couldn’t ship the heaviest package. On the other hand, capacity need not be more than sum(weights), because then we can ship all packages in just one day. In other words. the lower bound is max(A) for binary search, while the upper bound is sum(A).
class Solution:
    def shipWithinDays(self, weights: List[int], D: int) -> int:
        def feasible(capacity):
            days = 1
            local = 0
            for w in weights:
                local+=w
                if local>capacity:
                    local = w
                    days+=1
                    if days>D:
                        return False
            return True
                    
        left, right = max(weights), sum(weights)
        while left < right:
            mid = left + (right-left)//2
            if feasible(mid):
                right = mid
            else:
                left = mid + 1
                
        return left
  • Same approach; rehashed:
class Solution:
    def shipWithinDays(self, weights: List[int], D: int) -> int:
        left, right = max(weights), sum(weights)
        
        while left < right:
            mid, need, cur = (left + right) / 2, 1, 0
            for w in weights:
                if cur + w > mid:
                    need += 1
                    cur = 0
                cur += w
            if need > D: left = mid + 1
            else: right = mid
            
        return floor(left)
Complexity
  • Time: \(O(n\log{m})\) where \(m = sum(weights)\) and \(weights\) is the input array containing \(n\) items
  • Space \(O(1)\)

[1060/Medium] Missing Element in Sorted Array

Problem

  • Given an integer array nums which is sorted in ascending order and all of its elements are unique and given also an integer k, return the k-th missing number starting from the leftmost number of the array.

  • Example 1:

Input: nums = [4,7,9,10], k = 1
Output: 5
Explanation: The first missing number is 5.
  • Example 2:
Input: nums = [4,7,9,10], k = 3
Output: 8
Explanation: The missing numbers are [5,6,8,...], hence the third missing number is 8.
  • Example 3:
Input: nums = [1,2,4], k = 3
Output: 6
Explanation: The missing numbers are [3,5,6,7,...], hence the third missing number is 6.
  • Constraints:
    • 1 <= nums.length <= 5 * 104
    • 1 <= nums[i] <= 107
    • nums is sorted in ascending order, and all the elements are unique.
    • 1 <= k <= 108

  • Follow up: Can you find a logarithmic time complexity (i.e., O(log(n))) solution?

  • See problem on LeetCode.

Solution: Linear scan

class Solution:
    def missingElement(self, nums: List[int], k: int):
        
        for i in range(1, len(nums)):
            # number of missing elements between one index and the prior
            diff = nums[i] - nums[i-1] - 1 
            if diff >= k:
                return nums[i-1] + k 
            else:
                k -= diff  
        
        return nums[-1] + k
  • Similar approach:
class Solution:
    def missingElement(self, nums: List[int], k: int) -> int:
        
        #Approach: 
        # Step 1: find maximum possible kth number provided we had only one digit in array.
        # if will be (nums[0] + k)
        
        # Step2: nums[0] + k would have been the answer if there were no other digits, but if we have than we need to find  number of digits which are less than nums[0] + k. 
        
        # what is the kth missing number for single digit x, it is x + k
        ans = nums[0] + k
        
        # if length is one then x + k will be the answer
        if len(nums) == 1:
            return ans
        
        # if length is greater than one, we try to find how many numbers are less than
        # the maximum possible kth missing number (x+k)
        # whenever we encounter that there exist a number that is less than (x+k) we increase the (x+k) by 1
        # as soon as our ans (x+k) is greater than any number in the list, we return ans.
        for currentNum in nums[1:]:
            if currentNum > ans:
                return ans
            if currentNum <= ans:
                ans += 1
                
        return ans
Complexity
  • Time: \(O(n)\)
  • Space \(O(1)\)

Solution: Binary Search

  • The idea is to find the first index that has more missing elements than k using binary search.
  • For an input of nums = [4,7,9,10], let’s consider the number of missing elements at the second index. They are [5,6], i.e., 2 missing elements. This can be written as: num[1] - num[0] - 1. For index i, this can be generalized to nums[i] - nums[0] - i.
  • Finally, to get the first missing element, you can do num[0] + k + 0. Generalizing this, you get num[i] + k + i.
class Solution:
    def missingElement(self, nums: List[int], k: int) -> int:
        def calculateMissings(i):
            return nums[i] - nums[0] - i
                    
        left, right = 0, len(nums)

        # find the first index that has more missing elements than `k` using binary search
        # i.e., the lower bound
        while left < right:
            middle = (left + right) // 2
            
            # select the middle element in the array and compare it against the target
            if calculateMissings(middle) < k: 
                left = middle + 1
            else:
                right = middle
            
        return nums[0] + k + left - 1
Complexity
  • Time: \(O(n\log{n})\)
  • Space \(O(1)\)

[1231/Hard] Divide Chocolate

Problem

  • You have one chocolate bar that consists of some chunks. Each chunk has its own sweetness given by the array sweetness.

  • You want to share the chocolate with your k friends so you start cutting the chocolate bar into k + 1 pieces using k cuts, each piece consists of some consecutive chunks.

  • Being generous, you will eat the piece with the minimum total sweetness and give the other pieces to your friends.

  • Find the maximum total sweetness of the piece you can get by cutting the chocolate bar optimally.

  • Example 1:

Input: sweetness = [1,2,3,4,5,6,7,8,9], k = 5
Output: 6
Explanation: You can divide the chocolate to [1,2,3], [4,5], [6], [7], [8], [9]
  • Example 2:
Input: sweetness = [5,6,7,8,9,1,2,3,4], k = 8
Output: 1
Explanation: There is only one way to cut the bar into 9 pieces.
  • Example 3:
Input: sweetness = [1,2,2,1,2,2,1,2,2], k = 2
Output: 5
Explanation: You can divide the chocolate to [1,2,2], [1,2,2], [1,2,2]
  • Constraints:
    • 0 <= k < sweetness.length <= 104
    • 1 <= sweetness[i] <= 105
  • See problem on LeetCode.

Solution: Binary Search

class Solution:
    def maximizeSweetness(self, sweetness: List[int], k: int) -> int:
        left, right = 1, sum(sweetness) // (k + 1)
        
        while left < right:
            mid = (left + right + 1) // 2
            cur = cuts = 0
            
            for chunk in sweetness:
                cur += chunk
                if cur >= mid:
                    cuts += 1
                    cur = 0
            if cuts > k:
                left = mid
            else:
                right = mid - 1
                
        return right
  • Note that in this question, we want to find the maximum total sweetness. We have to find the rightmost value, so we use int mid = (left + right + 1)/2 and if (condition passed) left = mid; else right = mid - 1. For a question like Capacity to Ship Packages Within D Days, we want to find the leftmost value. So we have to use something like int mid = (left + right) / 2 and if (condition passed) right = mid; else left = mid + 1.
Complexity
  • Time: \(O(n\log{m})\) where \(m = sum(sweetness)\) and \(sweetness\) is the input array containing \(n\) items
  • Space \(O(1)\)

[1283/Medium] Find the Smallest Divisor Given a Threshold

Problem

  • Given an array of integers nums and an integer threshold, we will choose a positive integer divisor, divide all the array by it, and sum the division’s result. Find the smallest divisor such that the result mentioned above is less than or equal to threshold.

  • Each result of the division is rounded to the nearest integer greater than or equal to that element. (For example: 7/3 = 3 and 10/2 = 5).

  • The test cases are generated so that there will be an answer.

  • Example 1:

Input: nums = [1,2,5,9], threshold = 6
Output: 5
Explanation: We can get a sum to 17 (1+2+5+9) if the divisor is 1. 
If the divisor is 4 we can get a sum of 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2).
  • Example 2:
Input: nums = [44,22,33,11,1], threshold = 5
Output: 44
  • Constraints:
    • 1 <= nums.length <= 5 * 104
    • 1 <= nums[i] <= 106
    • nums.length <= threshold <= 106
  • See problem on LeetCode.

Solution: Binary Search

  • If sum > threshold, the divisor is too small.
  • If sum <= threshold, the divisor is big enough.
class Solution:
    def smallestDivisor(self, nums: List[int], threshold: int) -> int:
        l, r = 1, max(nums)
        while l < r:
            m = (l + r) // 2
            if sum(math.ceil(num / m) for num in nums) > threshold:
            # or if sum((num + m - 1) // m for num in nums) > threshold:
                l = m + 1
            else:
                r = m
        return l

  • Note that (p + m - 1) / m is equal to ceil(p / m).

  • Same approach; rehashed:

    • If a number is large enough, it will definitely have a result less than threshold; we need to find the smallest number that can do this.
    • How to check whether a given number can make the result less than or equal to threshold?
      • Just do a one pass on nums and see if the sum of the ceil of each division is less than or equal to threshold.
    • If given mid is a ok number, then we want to see if a smaller number can do the same thing, so
      • if ok(mid) is True: r = mid-1
      • else: l = mid+1
class Solution:
    def smallestDivisor(self, nums: List[int], threshold: int) -> int:
        def ok(mid):
            ans = 0
            for num in nums:
                ans += math.ceil(num / mid)
                if ans > threshold: return False
            return True    
            
        l, r = 1, int(1e6)
        while l <= r:
            mid = (l+r) // 2
            if ok(mid): r = mid - 1
            else: l = mid + 1
            
        return l
Complexity
  • Time: \(O(n\log{m})\) where \(m = max(A)\) and \(A\) is the input array containing \(n\) items
  • Space \(O(1)\)

[1482/Medium] Minimum Number of Days to Make \(m\) Bouquets

Problem

  • You are given an integer array bloomDay, an integer m and an integer k.

  • You want to make m bouquets. To make a bouquet, you need to use k adjacent flowers from the garden.

  • The garden consists of n flowers, the i-th flower will bloom in the bloomDay[i] and then can be used in exactly one bouquet.

  • Return the minimum number of days you need to wait to be able to make m bouquets from the garden. If it is impossible to make m bouquets return -1.

  • Example 1:

Input: bloomDay = [1,10,3,10,2], m = 3, k = 1
Output: 3
Explanation: Let us see what happened in the first three days. x means flower bloomed and _ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: [x, _, _, _, _]   // we can only make one bouquet.
After day 2: [x, _, _, _, x]   // we can only make two bouquets.
After day 3: [x, _, x, _, x]   // we can make 3 bouquets. The answer is 3.
  • Example 2:
Input: bloomDay = [1,10,3,10,2], m = 3, k = 2
Output: -1
Explanation: We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
  • Example 3:
Input: bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3
Output: 12
Explanation: We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: [x, x, x, x, _, x, x]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: [x, x, x, x, x, x, x]
It is obvious that we can make two bouquets in different ways.
  • Constraints:
    • bloomDay.length == n
    • 1 <= n <= 105
    • 1 <= bloomDay[i] <= 109
    • 1 <= m <= 106
    • 1 <= k <= n
  • See problem on LeetCode.

Solution: Binary Search

  • If m * k > n, it’s impossible, so return -1.
  • Otherwise, we deem it a possible task, so we can binary search the result.
    • left = 1 is the smallest number of days,
    • right = max(bloomDay) is big enough to make m bouquets.
  • Next, we are going to binary search in range [left, right].
  • Given mid days, we can know which flowers blooms.
  • Now the problem is, given an array of True and False, find out how many adjacent True bouquets are there in total.
  • If bouq < m, mid is still small for m bouquet. So we set left = mid + 1.
  • If bouq >= m, mid is big enough for m bouquet. So we set right = mid
class Solution:
    def minDays(self, bloomDay: List[int], m: int, k: int) -> int:
        if m * k > len(bloomDay): return -1
        left, right = 1, max(bloomDay)
        
        while left < right:
            mid = (left + right) // 2
            flow = bouq = 0
            for a in bloomDay:
                flow = 0 if a > mid else flow + 1
                if flow >= k:
                    flow = 0
                    bouq += 1
                    if bouq == m: break
            if bouq == m:
                right = mid
            else:
                left = mid + 1
                
        return left
Complexity
  • Time: \(O(n\log{m})\) where \(m = max(bloomDay)\) and \(bloomDay\) is the input array containing \(n\) items
  • Space \(O(1)\)

[1539/Easy] Kth Missing Positive Number

Problem

  • Given an array arr of positive integers sorted in a strictly increasing order, and an integer k.

  • Find the k-th positive integer that is missing from this array.

  • Example 1:

Input: arr = [2,3,4,7,11], k = 5
Output: 9
Explanation: The missing positive integers are [1,5,6,8,9,10,12,13,...]. The 5th missing positive integer is 9.
  • Example 2:
Input: arr = [1,2,3,4], k = 2
Output: 6
Explanation: The missing positive integers are [5,6,7,...]. The 2nd missing positive integer is 6.
  • Constraints:
    • 1 <= arr.length <= 1000
    • 1 <= arr[i] <= 1000
    • 1 <= k <= 1000
    • arr[i] < arr[j] for 1 <= i < j <= arr.length
  • See problem on LeetCode.

Solution: Maintain a count for number of missed values

  • We could go one by one from 1 and check if the number contained in the list (converting a to set for faster checking) and maintain a counter for the number of missed values.
class Solution:
    def findKthPositive(self, a: List[int], k: int) -> int:
        s = set(a)
        cnt = 0
        for i in range(1, max(s)):
            if i not in s:
                cnt += 1
                if cnt == k:
                    return i
        return max(s) + k - cnt
Complexity
  • Time: \(O(L+\max(a))\) time, where L is the length of the array assuming Python set takes \(O(1)\) time insert or look up an element (the average case for a hash table). \(L\) for building the set and max(a) for the number of set queries.
  • Space \(O(1)\)

Solution: Maintain a count

  • Since the array is sorted, we could do better by going one pass over the array instead.
class Solution:
    def findKthPositive(self, a: List[int], k: int) -> int:
        cnt = 0
        j = 0
        
        for i in range(1, max(a)):
            if i < a[j]:
                cnt += 1
                if cnt == k:
                    return i
            else:
                j += 1
                if j >= len(a):
                    break
        return a[-1] + k - cnt
Complexity
  • Time: \(O(max(a))\)
  • Space \(O(1)\)

Solution: Maintain a count between adjacent integers

  • We do not need to increase the numbers one by one. All numbers between two adjacent integers in a can be updated to the counter at once.
class Solution:
    def findKthPositive(self, a: List[int], k: int) -> int:
        cnt, prev = 0, 0
        
        for x in a:
            old_cnt = cnt
            cnt += x - prev - 1
            
            if cnt >= k:
                return prev + k - old_cnt
            prev = x
            
        return a[-1] + k - cnt
Complexity
  • Time: \(O(n)\) where \(n = len(arr)\)
  • Space \(O(1)\)

Solution: Maintain a count between adjacent integers

  • But wait… Do we really need a counter? If there is no missing number, the a[i] should just be i+1. If there is a single missing number before a[i], a[i] should be just i+2. So on so forth. In general, if there are m missing numbers up to a[i], a[i] = i + m + 1. So, when we see a[i], we know there are a[i]-i-1 missing numbers up to it. If a[i]-i-1 >= k or a[i] > i+k, the k-th missing value must be between a[i-1] and a[i].

  • On the other hand, if there have already been i numbers in a, the k-th missing value must be at least k+i. We show that k+i is actually the value we are looking for. First, a[i] > i+k, so i+k cannot be a[i]. Neither can it be any a[j], j > i, because a is increasing and a[j] > a[i] > i+k. Can i+k appear before a[i]? If that is the case, say i+k = a[j] for some j < i, then we will have a[j] = i+k > j+k. That means we would have found an earlier location j that triggers the a[j] > j+k criterion, and we would have stopped over there.

  • The above analysis gives us this clean 4 lines of code:

class Solution:
    def findKthPositive(self, a: List[int], k: int) -> int:
        for i, x in enumerate(a):
            if x > i + k:
                return i + k
                
        return len(a) + k
Complexity
  • Time: \(O(n)\) where \(n = len(arr)\)
  • Space \(O(1)\)

Solution: Binary Search

  • Assume the final result is x, and there are m numbers present in the range of [1, x]. Binary search the m in range [0, len(A)].
  • If there are m numbers present, that is A[0], A[1] .. A[m-1], the number of missing under A[m] is len(A[m]) - 1 - m.
  • If A[m] - 1 - m < k, m is too small, we update left = m.
  • If A[m] - 1 - m >= k, m is big enough, we update right = m.
  • Note that when we exit the while loop, l = r, which equals to the number of missing numbers.
  • So the K-th positive number will be l + k.
class Solution:
    def findKthPositive(self, arr: List[int], k: int) -> int:
        l, r = 0, len(arr)
        
        while l < r:
            m = (l + r) // 2
            if arr[m] - 1 - m < k:
                l = m + 1
            else:
                r = m
                
        return l + k
Complexity
  • Time: \(O(\log{n})\) where \(n = len(arr)\)
  • Space \(O(1)\)

[1891/Medium] Cutting Ribbons

Problem

  • You are given an integer array ribbons, where ribbons[i] represents the length of the i-th ribbon, and an integer k. You may cut any of the ribbons into any number of segments of positive integer lengths, or perform no cuts at all.

    • For example, if you have a ribbon of length 4, you can:
      • Keep the ribbon of length 4,
      • Cut it into one ribbon of length 3 and one ribbon of length 1,
      • Cut it into two ribbons of length 2,
      • Cut it into one ribbon of length 2 and two ribbons of length 1, or
      • Cut it into four ribbons of length 1.

  • Your goal is to obtain k ribbons of all the same positive integer length. You are allowed to throw away any excess ribbon as a result of cutting.

  • Return the maximum possible positive integer length that you can obtain k ribbons of, or 0 if you cannot obtain k ribbons of the same length.

  • Example 1:

Input: ribbons = [9,7,5], k = 3
Output: 5
Explanation:
- Cut the first ribbon to two ribbons, one of length 5 and one of length 4.
- Cut the second ribbon to two ribbons, one of length 5 and one of length 2.
- Keep the third ribbon as it is.
Now you have 3 ribbons of length 5.
  • Example 2:
Input: ribbons = [7,5,9], k = 4
Output: 4
Explanation:
- Cut the first ribbon to two ribbons, one of length 4 and one of length 3.
- Cut the second ribbon to two ribbons, one of length 4 and one of length 1.
- Cut the third ribbon to three ribbons, two of length 4 and one of length 1.
Now you have 4 ribbons of length 4.
  • Example 3:
Input: ribbons = [5,7,9], k = 22
Output: 0
Explanation: You cannot obtain k ribbons of the same positive integer length.
  • Constraints:
    • 1 <= ribbons.length <= 105
    • 1 <= ribbons[i] <= 105
    • 1 <= k <= 109

Solution: Binary search

  • The crux of the problem is implementing Binary Search.
  • The goal is to figure out what the maximum length of a ribbon could be so that we get k ribbons of that max length.
  • One way to think of it would be that the ribbon length could be anywhere from 1 to the max length of the a ribbon available in the list.
  • So what we do is go through the list (using Binary Search since we need to optimize linear search), find the mid of the given array and then iterate through the list testing the length with each element and summing the number of ribbons that can be made with the mid value. Then change mid accordingly.
class Solution:
    def maxLength(self, ribbons: List[int], k: int) -> int:
        # impossible case: when total length sum of all ribbons are less than `k`
        s = sum(ribbons)
        if s < k: return 0
                
        # The minimum length of the ribbon that we can cut is 1
        start = 1
        # The maximum length of the ribbon can be the maximum element in the list
        end = max(ribbons)
        
        # In this binary search, we are trying to go through the origin list and figure out which integer(from 1 -> ribbon of max length) is the deired length for the the target k pieces
        while(start <= end):
            mid = start + (end - start) // 2
            res = 0
            
            for i in ribbons:
                res += i // mid
            # If the value is >= target, we know that there could be a larger integer that will satisfy the same conditon
            if res >= k:
                start = mid+1
            else:
            # If lesser than k, then there could be a value lesser than the mid that could satisfy the condition
                end = mid -1
        
        return end
Complexity
  • Time: \(O(n\log{m})\) where \(m = max(ribbons)\) and \(ribbons\) is the input array containing \(n\) items
  • Space \(O(1)\)

Further Reading