Distilled • LeetCode • BFS
- Pattern: BFS
Pattern: BFS
[116/Medium] Populating Next Right Pointers in Each Node
Problem
- You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
-
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to
NULL. -
Initially, all next pointers are set to
NULL. -
Example 1:
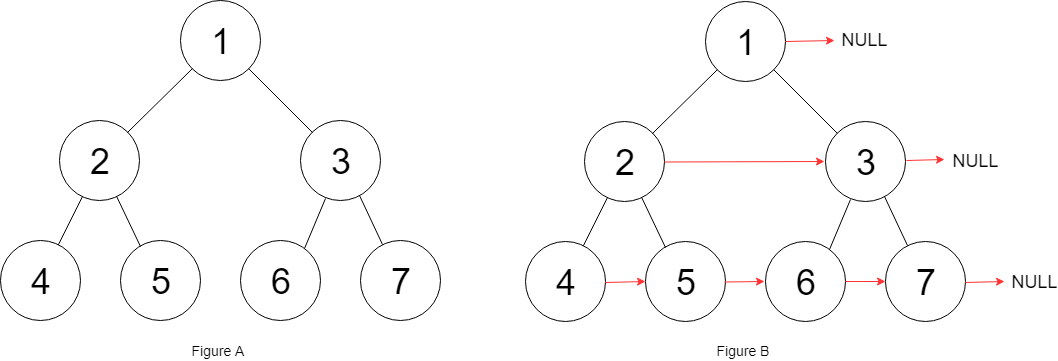
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
- Example 2:
Input: root = []
Output: []
- Constraints:
The number of nodes in the tree is in the range [0, 212 - 1].-1000 <= Node.val <= 1000
- Follow-up:
- You may only use constant extra space.
- The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.
- See problem on LeetCode.
Solution: Recursive level order traversal
-
Simply do it level by level, using the
next-pointers of the current level to go through the current level and set thenext-pointers of the next level. -
Note that this uses “real” O(1) space because of the many recursive solutions ignoring that recursion management (call stacks) needs space.
class Solution:
def connect(self, root: 'Node') -> 'Node':
Q = root
while root and root.left:
next = root.left
while root:
root.left.next = root.right
# Short-circuit AND: The expression x and y first evaluates x; if x is false, its value is returned; otherwise, y is evaluated and the resulting value is returned.
# same as root.right.next = None if not root.next else root.next.left
# Per https://docs.python.org/3.6/reference/expressions.html#boolean-operations
root.right.next = root.next and root.next.left
root = root.next
root = next
return Q
- Same approach; rehashed:
class Solution:
def connect(self, root: 'Node', next=None) -> 'Node':
if root is None: return None
root.next = next
self.connect(root.left, root.right)
self.connect(root.right, root.next.left if root.next else None)
return root
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: BFS + Queue
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return
queue = [root]
while queue:
curr = queue.pop(0)
if curr.left and curr.right:
curr.left.next = curr.right
if curr.next:
curr.right.next = curr.next.left
queue.append(curr.left)
queue.append(curr.right)
return root
Solution: BFS (without Queue)
- Since we are manipulating tree nodes on the same level, it’s easy to come up with a very standard BFS solution using queue.
- But because of
nextpointer, we actually don’t need a queue to store the order of tree nodes at each level, we just use thenextpointer like it’s a link list at each level; in addition, we can borrow the idea used in the Binary Tree level order traversal problem, which uses thecurandnextpointer to store first node at each level; we exchangecurandnextevery time whencuris the last node at each level.
class Solution:
def connect(self, root: 'Node') -> 'Node':
"""
:type root: TreeLinkNode
:rtype: nothing
"""
if not root:
return None
cur = root
next = root.left
while next: # or while cur.left:
cur.left.next = cur.right
if cur.next:
cur.right.next = cur.next.left
cur = cur.next
else:
cur = next
next = cur.left
return root
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: BFS
- Same approach as above; rehashed (but worse time complexity):
class Solution:
def connect(self, root: 'Node') -> 'Node':
def populate_next_level(node):
# this function populates all of the next level of the current
# it needs to populate both left node and the right node
# left node's next sibling is always the right node
# right node's next sibling is current node's next sibling's left child, if there is a next
# then we iterate within the current level filling out all of the lower level
current_node = node
while current_node:
current_node.left.next = current_node.right
current_node.right.next = current_node.next and current_node.next.left
current_node = current_node.next
# first if root is empty return root
if not root:
return root
# then we need traverse at each level and populate the children starting from the very left node
# we will keep track of current node and its left child (1) for better readability
# (2) since we need to return the main root and thus we cant manipulate that
current = root
while current and current.left:
populate_next_level(current)
current = current.left
return root
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
Solution: DFS + Stack
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return
stack = [root]
while stack:
curr = stack.pop()
if curr.left and curr.right:
curr.left.next = curr.right
if curr.next:
curr.right.next = curr.next.left
stack.append(curr.right)
stack.append(curr.left)
return root
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)
[286/Medium] Walls and Gates
Problem
-
You are given an
m x ngridroomsinitialized with these three possible values.-1A wall or an obstacle.0A gate.INFInfinity means an empty room. We use the value2^31 - 1 = 2147483647to representINFas you may assume that the distance to a gate is less than2147483647.
-
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with
INF. -
Example 1:
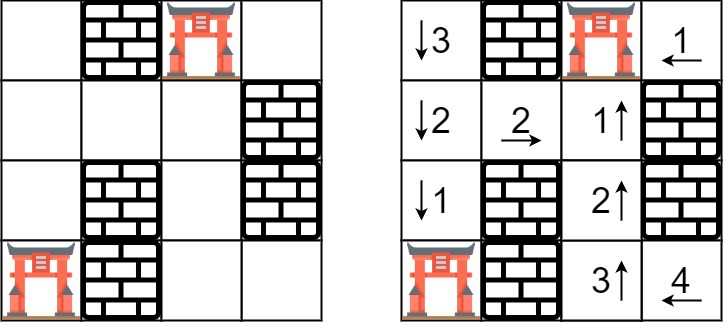
Input: rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647,2147483647]]
Output: [[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]
- Example 2:
Input: rooms = [[-1]]
Output: [[-1]]
- Constraints:
m == rooms.lengthn == rooms[i].length1 <= m, n <= 250rooms[i][j] is -1, 0, or 2^31 - 1.
- See problem on LeetCode.
Solution: DFS + Stack
- Note that this solution is not that efficient as the BFS one (below):
class Solution(object):
def wallsAndGates(self, rooms: List[List[int]]) -> None:
s = [(i, j, 0) for i, row in enumerate(rooms) for j, r in enumerate(row) if not r]
while s:
i, j, step = s.pop()
rooms[i][j] = step if rooms[i][j] > step else rooms[i][j]
for I, J in ((i+1, j),(i-1, j),(i, j+1),(i, j-1)):
if 0 <= I < len(rooms) and 0 <= J < len(rooms[0]) and rooms[I][J] > step:
s += (I, J, step + 1),
Solution: BFS + Deque
class Solution:
def wallsAndGates(self, rooms: List[List[int]]) -> None:
"""
Do not return anything, modify rooms in-place instead.
"""
queue = deque([])
for i in range(len(rooms)):
for j in range(len(rooms[0])):
if rooms[i][j] == 0:
queue.append([i, j])
# or simply queue = [(i, j) for i, row in enumerate(rooms) for j, r in enumerate(row) if not r]
while queue:
i, j = queue.popleft()
for r, c in [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]:
if 0 <= r < len(rooms) and 0 <= c < len(rooms[0]) and rooms[r][c] == 2147483647:
rooms[r][c] = rooms[i][j] + 1
queue.append([r, c]) # or queue += (r, c), or queue += [r, c],
Complexity
- Time: \(O(ke)\) - \(k\) is number of buildings and \(e\) is number of empty tiles - for each building we need to visit every empty tile
- Space: \(O(mn*k)\) - need to store every point of the grid and for those which have empty slots of land we need to store an array of k buildings
Solution: BFS with Pruning
- Use
hitto record how many times a0grid has been reached and usedistSumto record the sum of distance from all1grids to this0grid. A powerful pruning is that during the BFS we usecount1to count how many1grids we reached. Ifcount1 < buildingsthen we know not all1grids are connected are we can return-1immediately, which greatly improved speed. - Using
matrixto count the sum of distance and number of buildings that have visited this position:
class Solution:
def shortestDistance(self, grid: List[List[int]]) -> int:
if not grid or not grid[0]:
return -1
matrix = [[[0,0] for i in range(len(grid[0]))] for j in range(len(grid))]
cnt = 0 # count how many building we have visited
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
self.bfs([i,j], grid, matrix, cnt)
cnt += 1
res = float('inf')
for i in range(len(matrix)):
for j in range(len(matrix[0])):
if matrix[i][j][1] == cnt:
res = min(res, matrix[i][j][0])
return res if res != float('inf') else -1
def bfs(self, start, grid, matrix, cnt):
q = [(start, 0)]
while q:
tmp = q.pop(0)
po, step = tmp[0], tmp[1]
for dp in [(-1,0), (1,0), (0,1), (0,-1)]:
i, j = po[0]+dp[0], po[1]+dp[1]
# only the position be visited by cnt times will append to queue
if 0 <= i < len(grid) and 0 <= j < len(grid[0]) and matrix[i][j][1] == cnt and grid[i][j] == 0:
matrix[i][j][0] += step+1
matrix[i][j][1] = cnt+1
q.append(([i,j], step+1))
[314/Medium] Binary Tree Vertical Order Traversal
Problem
-
Given the root of a binary tree, return the vertical order traversal of its nodes’ values. (i.e., from top to bottom, column by column).
-
If two nodes are in the same row and column, the order should be from left to right.
-
Example 1:
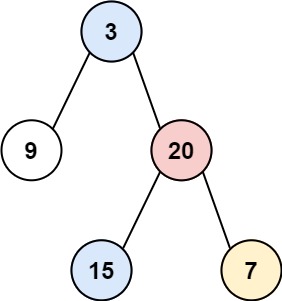
Input: root = [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
- Example 2:
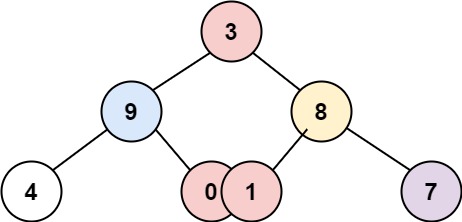
Input: root = [3,9,8,4,0,1,7]
Output: [[4],[9],[3,0,1],[8],[7]]
- Example 3:
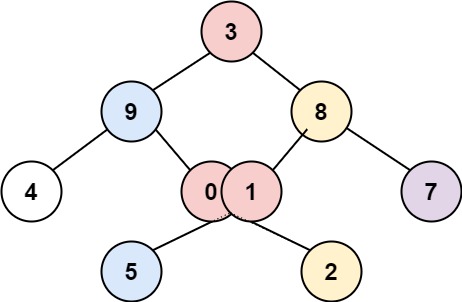
Input: root = [3,9,8,4,0,1,7,null,null,null,2,5]
Output: [[4],[9,5],[3,0,1],[8,2],[7]]
- Constraints:
The number of nodes in the tree is in the range [0, 100].-100 <= Node.val <= 100
- See problem on LeetCode.
Solution: BFS + Dict + Queue
class Solution:
def verticalOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
cols = collections.defaultdict(list)
queue = [(root, 0)]
for node, i in queue: # or while queue:
# node, i = queue.popleft()
if node:
cols[i].append(node.val)
queue += (node.left, i - 1), (node.right, i + 1)
return [cols[i] for i in sorted(cols)]
Complexity
- Time: \(O(n\log{n})\)
- Space: \(O(n)\) for the
queue
Solution: BFS + Dict + Deque
class Solution:
def verticalOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
res = collections.defaultdict(list)
queue = collections.deque([(root, 0)])
while queue:
node, pos = queue.popleft()
if node:
res[pos].append(node.val)
# going left? pos = pos-1; going right? pos = pos+1
queue += (node.left, pos-1), (node.right, pos+1)
return [res[i] for i in sorted(res)]
Complexity
- Time: \(O(n\log{n})\)
- Space: \(O(n)\) for the
resandqueue
[637/Easy] Average of Levels in Binary Tree
Problem
-
Given the
rootof a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted. -
Example 1:
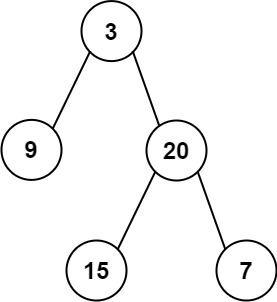
Input: root = [3,9,20,null,null,15,7]
Output: [3.00000,14.50000,11.00000]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return [3, 14.5, 11].
- Example 2:
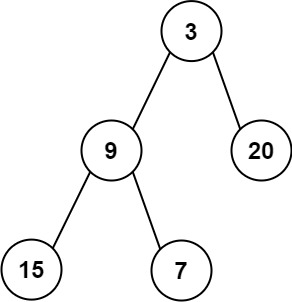
Input: root = [3,9,20,15,7]
Output: [3.00000,14.50000,11.00000]
- Constraints:
The number of nodes in the tree is in the range [1, 104].-231 <= Node.val <= 231 - 1
- See problem on LeetCode.
Solution: DFS + Defaultdict
- Do a DFS over a tree and save the sum and the number of nodes at every level.
- Then iterate over the levels and find the average for each.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
level_count = defaultdict(int)
level_sum = defaultdict(int)
def dfs_collect(node=root, level=0):
if not node: return
level_count[level] += 1
level_sum[level] += node.val
dfs_collect(node.left, level+1)
dfs_collect(node.right, level+1)
# step 1: traversal
dfs_collect()
# step 2: averaging
return [level_sum[i] / level_count[i] for i in range(len(level_count))]
Complexity
- Time: \(O(n) = O(n)\) where \(n\) is the number of nodes in the tree. Single traversal through all nodes.
- Space: \(O(l)\), where \(l\) is the number of levels.
Solution: BFS + Queue
-
A problem talking about levels in a binary tree should immediately bring to mind a breadth-first search (BFS) approach. The classic BFS approach for a binary tree is to use a queue and push each queue entry’s children onto the end of the queue. This way, the queue will run to the end of the row/level before moving onto the next level.
-
When a problem requires you to isolate a level, you can simply take the length of the queue at the start of the row and then once you’ve processed that many nodes from the queue, you’ll know that you’re ready to start the next row.
-
So as long as the queue exists, we’ll take each row, sum the row’s values (
row_sum), then divide by the length of the row (qlen) to find the average, pushing each average into our answer array (ans).
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
q, ans = [root], []
while len(q):
qlen, row_sum = len(q), 0
for _ in range(qlen):
# Note that when you do q.pop(0), you shift all values to the left.
# A deque would have been more appropriate instead, so removing the
# first element would be O(1) instead of O(N) time complexity.
curr = q.pop(0)
row_sum += curr.val
if curr.left:
q.append(curr.left)
if curr.right:
q.append(curr.right)
ans.append(row_sum/qlen)
return ans
Complexity
- Time: \(O(n + n) = O(n)\) where \(n\) is the total number of nodes. Single traversal through all nodes.
- Space: \(O(level with most amount of nodes/largest width)\), i.e., at most the largest amount of nodes stored is that of the widest level.
Solution: BFS + Deque
from collections import deque
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
queue = deque([root])
average_of_level = []
while queue:
# valid nodes on current level
size = len(queue)
totalSum = 0
for _ in range(size):
# pop one node from traversal queue
node = queue.popleft()
# accumulate sum of current level
totalSum += node.val
# add left child if it exists
if node.left:
queue.append(node.left)
# add right child if it exists
if node.right:
queue.append(node.right)
# add current level's average value to list
average_of_level.append(totalSum/size)
return average_of_level
Complexity
- Time: \(O(n)\) where \(n\) is the total number of nodes. Single traversal through all nodes.
- Space: \(O(level with most amount of nodes/largest width)\), i.e., at most the largest amount of nodes stored is that of the widest level.
[785/Medium] Is Graph Bipartite?
Problem
- There is an undirected graph with
nnodes, where each node is numbered between0andn - 1. You are given a 2D array graph, wheregraph[u]is an array of nodes that nodeuis adjacent to. More formally, for eachvingraph[u], there is an undirected edge between nodeuand nodev. The graph has the following properties:- There are no self-edges (
graph[u]does not containu). - There are no parallel edges (
graph[u]does not contain duplicate values). - If
vis ingraph[u], thenuis ingraph[v](the graph is undirected). - The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
- There are no self-edges (
-
A graph is bipartite if the nodes can be partitioned into two independent sets
AandBsuch that every edge in the graph connects a node in setAand a node in setB. -
Return
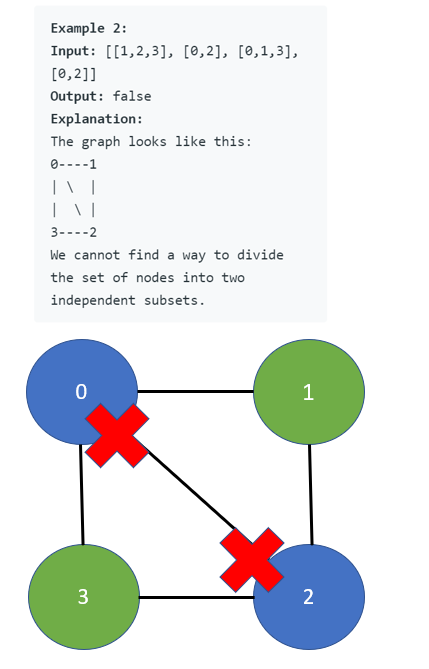
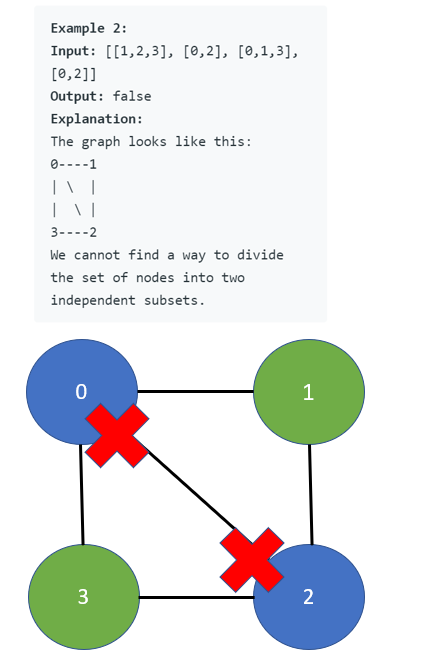
trueif and only if it is bipartite. - Example 1:
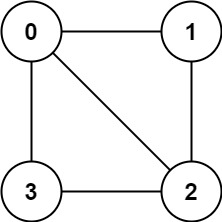
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
- Example 2:
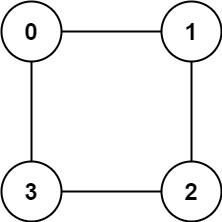
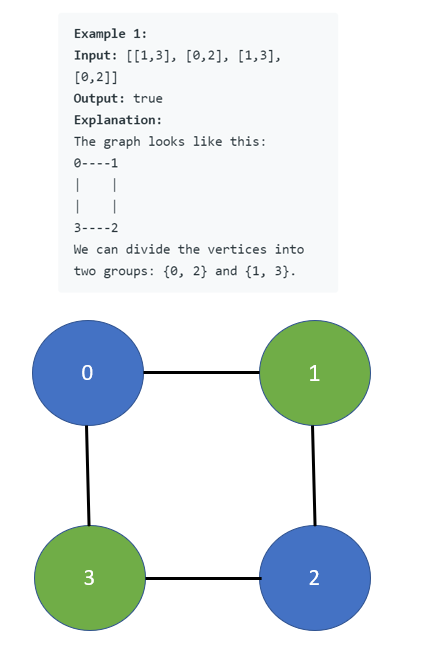
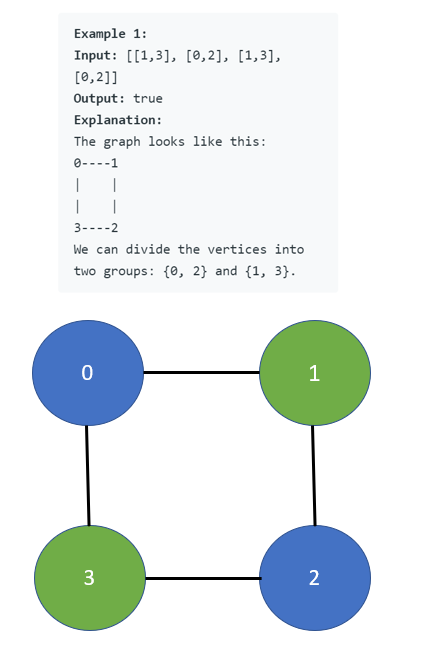
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
- Constraints:
graph.length == n1 <= n <= 1000 <= graph[u].length < n0 <= graph[u][i] <= n - 1graph[u] does not contain u.All the values of graph[u] are unique.If graph[u] contains v, then graph[v] contains u.
- See problem on LeetCode.
Solution: DFS + Coloring using a Stack
- Per Wikipedia: Bipartite Graph, a graph is bipartite if and only if it is 2-colorable (meaning that we can color the graph such that no two adjacent nodes/vertices are of the same color with only 2 colors), we can attempt to 2-color the graph by traversing the graph and marking the neighbors of a node to be a different color than the color of the node. If we successfully 2-color the graph, we can return
True, but if we come across two adjacent vertices of the same colors, we must returnFalse.
- We can implement this algorithm by running DFS search with a Stack starting from every node in the graph (remember, there is no guarantee that the input graph is connected), while keeping a single
visitedset across BFS searches to prevent redundant searches.
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
visited = set()
two_color = [set(), set()]
for i in range(len(graph)):
if i not in visited:
stack = [(i, 1)]
while stack:
# poping the element at the end of the array
node, color = stack.pop()
visited.add(node)
two_color[color].add(node)
for neighbor in graph[node]:
if neighbor in two_color[color]:
return False
if neighbor not in visited:
# appending the new node at the end of the array
stack.append((neighbor, -1 * color))
return True
Complexity
- Time: \(O(\|E\|+\|V\|)\) time, where \(\|E\|\) is the number of edges and \(\|V\|\) is the number of nodes/vertices in the input graph.
- Space: \(O(n)\) for
stack
Solution: BFS + Coloring using a Deque
- Use BFS to traverse the graph with a deque.
- Each pair of connected nodes
A <-> Bcannot have same color. We use1to mark A and-1to mark B. - If we have a node was seen before and the color does not match, this means this node violate the bipartite condition.
- Repeat this process for all nodes since not all the nodes are connected, in other words, the graph may have different disjoint components.
import collections
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
seen = {}
for i in range(len(graph)):
if i not in seen:
dq = collections.deque([(i, 1)]) # 1 is just the starting color, could be -1 also
while dq:
node, color = dq.popleft()
if node in seen:
if color == seen[node]:
continue
else:
# if we a node was seen before and the color does not match,
# this means this node violates the bipartite condition
return False
seen[node] = color
for neighbor in graph[node]:
# appending the new node at the end of the array with an inverted color as the current node
dq.append((neighbor, color * (-1)))
return True
Complexity
- Time: \(O(\|E\|+\|V\|)\) time, where \(\|E\|\) is the number of edges and \(\|V\|\) is the number of nodes/vertices in the input graph.
- Space: \(O(n)\) for
dq
[958/Medium] Check Completeness of a Binary Tree
Problem
-
Given the
rootof a binary tree, determine if it is a complete binary tree. -
In a complete binary tree, every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between
1and2^hnodes inclusive at the last level h. -
Example 1:

Input: root = [1,2,3,4,5,6]
Output: true
Explanation: Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.
- Example 2:

Input: root = [1,2,3,4,5,null,7]
Output: false
Explanation: The node with value 7 isn't as far left as possible.
- Constraints:
The number of nodes in the tree is in the range [1, 100].1 <= Node.val <= 1000
- See problem on LeetCode.
Solution: BFS + Deque
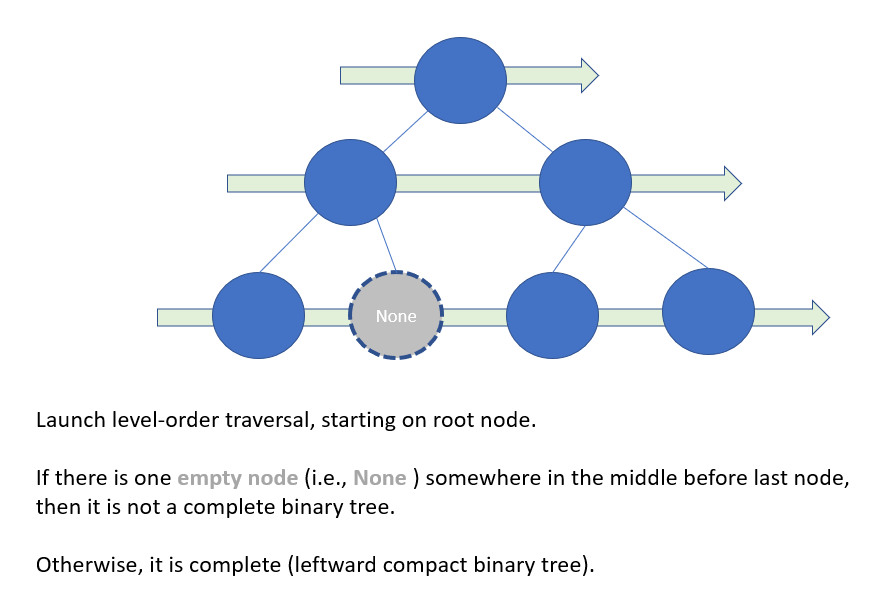
- Complete binary tree is a “complete” leftward compact tree.
- Launch level-order-traversal (or BFS if we see binary tree as a single source graph on root)
- If there is an empty node (i.e.
None) somewhere in the middle before last node, then it is not a complete binary tree, thus return False. - Otherwise, it is complete and return True.
from collections import deque
class Solution:
def isCompleteTree(self, root: TreeNode) -> bool:
traversal_queue = deque([root])
prev_node = root
# Launch Level-order traversal
while traversal_queue:
cur_node = traversal_queue.popleft()
if cur_node:
if not prev_node:
# Empty node in the middle means this is not a complete binary tree (not left-compact)
return False
traversal_queue.append(cur_node.left)
traversal_queue.append(cur_node.right)
# update previous node
prev_node = cur_node
return True
Complexity
- Time: \(O(n)\)
- Space: \(O(1)\)